Search
Duplicate

AI/ Markov Models, Hidden Markov Models(HMM)

Markov Models

Markov Model은 시퀀스를 모델링하는 동적 모델로 현재 상태 xt\bold{x}_t가 오직 과거의 상태 xt−1\bold{x}_{t-1}에만 의존한다는 Markov Assumption을 갖는 모델이다.
다시 말해 xt\bold{x}_t가 시스템의 상태에 관한 모든 관련된 정보를 포착한다고 가정하자. 이것은 주어진 과거가 미래를 예측하는 것에 대한 충분 통계량(sufficient statistic)이라는 뜻이다. 즉
p(xt+τ∣xt,x1:t−1)=p(xt+τ∣xt)p(\bold{x}_{t+\tau}|\bold{x}_t,\bold{x}_{1:t-1}) = p(\bold{x}_{t+\tau}|\bold{x}_t)
모든 τ≥0\tau \ge 0에 대해 이것은 Markov assumption이라고 부른다. 이 경우에 모든 유한 길이의 시퀀스에 대해 결합 분포를 다음과 같이 작성할 수 있다.
p(x1:T)=p(x1)p(x2∣x1)p(x3∣x2)p(x4∣x3)...=p(x1)∏t=2Tp(xt∣xt−1)p(\bold{x}_{1:T}) = p(\bold{x}_1)p(\bold{x}_2|\bold{x}_1)p(\bold{x}_3|\bold{x}_2)p(\bold{x}_4|\bold{x}_3)... = p(\bold{x}_1) \prod_{t=2}^T p(\bold{x}_t|\bold{x}_{t-1})
이것을 Markov chain 또는 Markov model이라 부른다.

Hidden Markov Models(HMM)

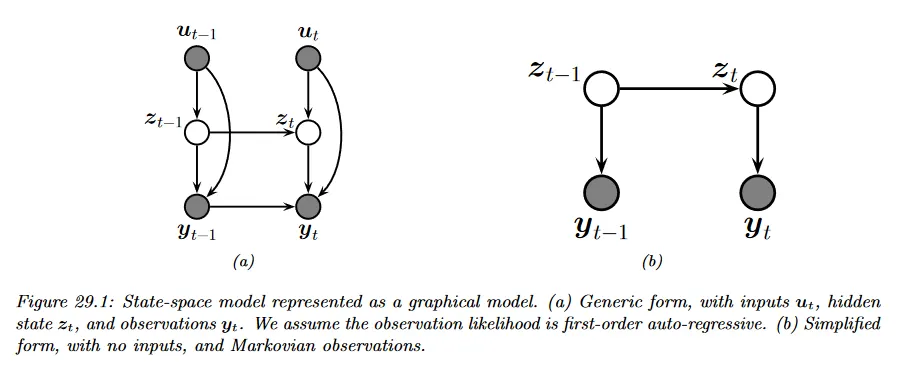
Hidden Markov Models은 Markov Model에 은닉 상태 zt\bold{z}_{t}가 추가된 버전으로 관찰 yt\bold{y}_t이 아닌 은닉 상태 zt\bold{z}_{t}가 Markov Process를 따르고, 현재 관찰 yt\bold{y}_t을 생성하는 모델이다. 현재 관찰 yt\bold{y}_t은 과거 관찰 yt−1\bold{y}_{t-1} 에 영향을 받지 않고 오직 현재 은닉 상태 zt\bold{z}_{t}에만 영향을 받는다. 아래 그림의 (b) 참조.
그러나 현재 관찰 yt\bold{y}_t이 과거 관찰 yt−1\bold{y}_{t-1} 에 영향을 받지 않는다는 가정은 다소 제한적이기 때문에 위의 그림 (a)와 같이 관찰 yt−1\bold{y}_{t-1}에도 영향을 받는다고 가정하면 Auto-Regressive HMM이 된다. 이것은 State-Space Model(SSM)의 형식이 된다.
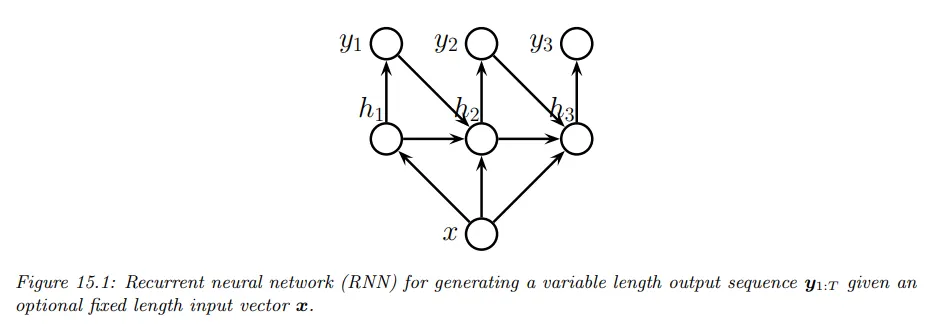
만일 관찰 yt\bold{y}_t이 과거 관찰 yt−1\bold{y}_{t-1}에 영향 받지 않고 현재 은닉 상태 zt\bold{z}_{t}에만 영향 받지만, 현재 은닉 상태 zt\bold{z}_{t}가 과거 관찰(출력) yt−1\bold{y}_{t-1}에 영향을 받는다면 (Vec2Seq) RNN 모델 형식이 된다.

참고

Made with