Search
Duplicate

AI/ Discrete DDPM(D3PM)

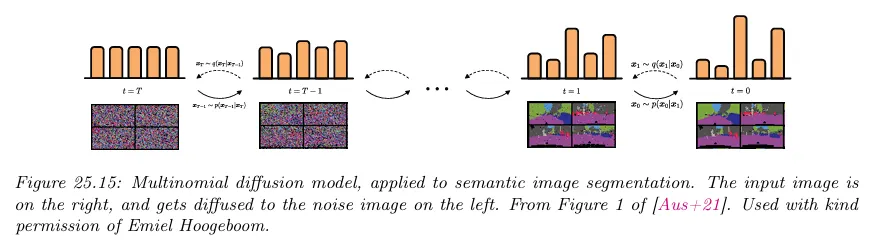
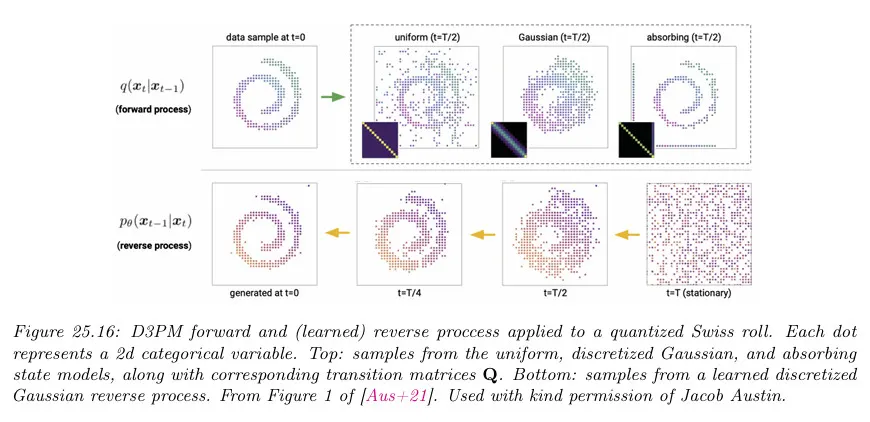
Discrete Denoising Diffusion Probabilistic Model (D3PM)

이산 상태 공간이나 이산 시간 diffusion 프로세스를 직접 정의하는 것을 Discrete Denoising Diffusion Probabilistic Model(D3PM)이라 한다. 기본적인 아이디어는 semantic segmentation의 맥락에서 아래 그림 참조. 여기서 카테고리컬 라벨을 이미지의 각 픽셀에 연관시킬 수 있다.
효과적인 학습을 보장하려면 다음 조건들을 만족해야 한다.
•
임의의 timestep tt에 대해 q(xt∣x0)q(\bold{x}_t|\bold{x}_0)에서 효과적으로 샘플할 수 있어야한다. 그래야만 variational bound를 최적화 할 때 무작위로 timestep를 샘플할 수 있다.
•
q(xt−1∣xt,x0)q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0)가 다루기 쉬운 형태여야 한다. 그래야만 KL 항을 효과적으로 계산할 수 있다.
•
forward 프로세스가 prior p(xT)p(\bold{x}_T)를 생성하는데 사용할 수 있는 알려진 고정 분포 π(xT)\pi(\bold{x}_T)로 수렴하면 유용하다. 이것은 DKL(q(xT∣x0)∥p(xT))=0D_\text{KL}(q(\bold{x}_T|\bold{x}_0)\|p(\bold{x}_T)) = 0을 보장한다.
위의 기준을 만족시키기 위해 상태가 각각 카테고리컬 값 xt∈{1,...,K}x_t \in \{1,...,K\}을 나타내는 DD개 독립 블록으로 구성되었다고 가정한다. 이것을 원핫 row 벡터 x0\bold{x}_0으로 표현한다. 일반적으로 이것은 확률 벡터를 표현한다. 그 다음 forward diffusion 커널을 다음처럼 정의한다.
q(xt∣xt−1)=Cat(xt∣xt−1Qt)q(\bold{x}_t|\bold{x}_{t-1}) = \text{Cat}(\bold{x}_t|\bold{x}_{t-1}\bold{Q}_t)
여기서 [Qt]ij=q(xt=j∣xt−1=k)[\bold{Q}_t]_{ij} = q(x_t=j|x_{t-1}=k)는 row stochastic transition 행렬이다. Qt\bold{Q}_t를 어떻게 정의하는지는 아래 ‘Choice of Markov transition matrices’에서 논의한다.
forward 프로세스의 tt-단계 marginal을 다음처럼 유도할 수 있다.
q(xt∣x0)=Cat(xt∣x0Qˉt)Qˉt=Q1Q2...Qt\begin{aligned} q(\bold{x}_t|\bold{x}_0) &= \text{Cat}(\bold{x}_t|\bold{x}_0\bar{\bold{Q}}_t)\\ \bar{\bold{Q}}_t &= \bold{Q}_1\bold{Q}_2...\bold{Q}_t \end{aligned}
유사하게 forward 프로세스를 다음과 같이 reverse 할 수 있다.
q(xt−1∣xt,x0)=q(xt∣xt−1,x0)q(xt−1∣x0)q(xt∣x0)=Cat(xt−1∣xtQt⊤⊙x0Qˉt−1x0Qˉtxt⊤)\begin{aligned} q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0) &= {q(\bold{x}_t|\bold{x}_{t-1},\cancel{\bold{x}_0})q(\bold{x}_{t-1}|\bold{x}_0) \over q(\bold{x}_t|\bold{x}_0)} \\&= \text{Cat}\left(\bold{x}_{t-1}|{\bold{x}_t\bold{Q}_t^\top \odot \bold{x}_0\bar{\bold{Q}}_{t-1} \over \bold{x}_0\bar{\bold{Q}}_t\bold{x}_t^\top} \right) \end{aligned}
생성 프로세스 pθ(xt−1∣xt)p_{\boldsymbol{\theta}}(\bold{x}_{t-1}|\bold{x}_t)을 어떻게 정의하는지 아래의 ‘Parameterization of the reverse process’ 부분에서 논의한다.

Choice of Markov transition matrices

forward process를 위한 전이 행렬 Q\bold{Q}를 표현하는 단순한 접근은 다음과 같이 스칼라 형식으로 작성할 수 있는 Qt=(1−βt)I+βt/K\bold{Q}_t = (1-\beta_t)\bold{I} + \beta_t/K를 사용하는 것이다.
[Qt]ij={1−K−1Kβti=j1Kβti≠j[\bold{Q}_t]_{ij} = \begin{cases} 1 - {K-1 \over K}\beta_t & i = j \\ {1\over K} \beta_t & i \ne j \end{cases}
직관적으로 이것은 KK개 클래스에 약간의 균등 노이즈를 추가하고 큰 확률 1−βt1-\beta_t로, xt−1\bold{x}_{t-1}에서 샘플한다. 이것을 uniform kernel이라 부른다. 이것은 엄격하게 양의 요소를 갖는 doubly stochastic 행렬(모든 행과 열의 합이 1인 비음수 정사각 행렬)이기 때문에 stationary 분포는 균등이다. 아래 그림 참조
균등 커널의 경우에 marginal 분포가 다음처럼 주어지는 것을 보일 수 있다.
q(xt∣x0)=Cat(xt∣αˉtx0+(1−αˉt)/K)q(\bold{x}_t|\bold{x}_0) = \text{Cat}(\bold{x}_t|\bar{\alpha}_t\bold{x}_0 + (1-\bar{\alpha}_t)/K)
여기서 αt=1−βt\alpha_t = 1-\beta_t이고 αˉt=∏τ=1tατ\bar{\alpha}_t = \prod_{\tau=1}^t \alpha_\tau. 이것은 가우시안 경우와 유사하다. 게다가 posterior 분포를 다음처럼 유도할 수 있다.
q(xt−1∣xt,x0)=Cat(xt−1∣θpost(xt,θ0))θpost(xt,θ0)=θ~/∑k=1Kθ~lθ~=[αtxt+(1−αk)/K]⊙[αˉt−1x0+(1−αˉt−1)/K]\begin{aligned} q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0) &= \text{Cat}(\bold{x}_{t-1}|\boldsymbol{\theta}_\text{post}(\bold{x}_t,\boldsymbol{\theta}_0))\\ \boldsymbol{\theta}_\text{post}(\bold{x}_t,\boldsymbol{\theta}_0) &= \tilde{\boldsymbol{\theta}}/\sum_{k=1}^K \tilde{\theta}_l \\ \tilde{\boldsymbol{\theta}} &= [\alpha_t \bold{x}_t + (1-\alpha_k)/K] \odot [\bar{\alpha}_{t-1}\bold{x}_0 + (1-\bar{\alpha}_{t-1})/K] \end{aligned}
또 다른 옵션은 확률 βt\beta_t으로 전이하는 MASK 토큰을 나타내는 특별한 absorbing state mm을 정의하는 것이다. 형식적으로 Qt=(1−βt)I+βt1em⊤\bold{Q}_t = (1-\beta_t)\bold{I} + \beta_t\bold{1e}_m^\top 또는 스칼라 형식으로 다음과 같다.
[Qt]ij={1i=j=m1−βti=j≠mβtj=m,i≠m[\bold{Q}_t]_{ij} = \begin{cases} 1 & i = j = m \\ 1-\beta_t & i = j \ne m \\ \beta_t & j=m, i\ne m \end{cases}
이것은 상태 mm의 점-질량(point-mass) 분포로 수렴한다.
또 다른 옵션은 ordinal 양자화된 값에 적합한 discretized Gaussian을 사용하는 것이다. 이 분포는 상태들의 수치적 유사성에 따라 인접한 다른 상태로 전이할 확률을 갖는다. 전이 행렬이 doubly stochastic 임을 보장하면 결과 stationary 분포는 다시 uniform이다.

Parameterization of the reverse process

신경망 fθ(xt)f_{\boldsymbol{\theta}}(\bold{x}_t)를 사용하여 logit pθ(xt−1∣xt)p_{\boldsymbol{\theta}}(\bold{x}_{t-1}|\bold{x}_t)를 직접 예측하는 것이 가능하지만, p~θ(x~0∣xt)\tilde{p}_{\boldsymbol{\theta}}(\tilde{\bold{x}}_{0}|\bold{x}_t)을 사용하여 출력의 logit을 직접 예측하는 것이 더 바람직하다. 그러면 이것을 q(xt−1∣xt,x0)q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0)에 대한 해석적 표현식과 결합하여 다음을 얻을 수 있다.
pθ(xt−1∣xt)∝∑x~0q(xt−1∣xt,x~0)p~θ(x~0∣xt)p_{\boldsymbol{\theta}}(\bold{x}_{t-1}|\bold{x}_t) \propto \sum_{\tilde{\bold{x}}_0} q(\bold{x}_{t-1}|\bold{x}_t,\tilde{\bold{x}}_0)\tilde{p}_{\boldsymbol{\theta}}(\tilde{\bold{x}}_0|\bold{x}_t)
pθ(xt−1∣xt)p_{\boldsymbol{\theta}}(\bold{x}_{t-1}|\bold{x}_t)를 직접 학습하는 것과 비교하여 이 접근의 한 가지 이점은 모델이 Qt\bold{Q}_t에서 모든 희소성 제약을 자동적으로 만족한다는 것이다. 게다가 한 번에 kk 단계 추론을 수행하여 다음을 예측할 수 있다.
pθ(xt−k∣xt)∝∑x~0q(xt−k∣xt,x~0)p~θ(x~0∣xt)p_{\boldsymbol{\theta}}(\bold{x}_{t-k}|\bold{x}_t) \propto \sum_{\tilde{\bold{x}}_0} q(\bold{x}_{t-k}|\bold{x}_t,\tilde{\bold{x}}_0)\tilde{p}_{\boldsymbol{\theta}}(\tilde{\bold{x}}_0|\bold{x}_t)
multi-step 가우시안 경우에 멀티모달리티를 다루기 위해 더 복잡한 모델이 필요하지만 이산 분포는 이러한 유연성이 이미 내재되어 있다.

Noise schedules

이산화된 가우시안 diffusion에 대해 이산화 단계 전에 가우시안 노이즈의 선형으로 증가하는 분산을 제안했다.
균등 diffusion에 대해 αt=cos⁡(t/T+s1+sπ2)\alpha_t = \cos ({t/T+s \over 1+s}{\pi \over 2}) 형식의 cosine 스케쥴을 사용할 수 있다. 여기서 s=0.08s=0.08. (βt=1−αt\beta_t = 1-\alpha_t임을 떠올려라. 따라서 노이즈는 시간이 지남에 따라 증가한다.)
masked diffusion에 대해 βt=1/(T−t+1)\beta_t = 1/(T-t+1) 형식의 스케쥴을 사용할 수 있다.

Connections to other probabilistic models for discrete sequences

D3PM과 다른 확률적 텍스트 모델 사이에 흥미로운 관계가 있다. 예컨대 적절한 전이행렬을 사용하고 토큰의 α=10\alpha = 10%를 MASK로 교체하고 β=5\beta = 5%를 무작위로 균일하게 교체하는 한 단계 diffusion 프로세스의 경우, BERT 언어 모델을 학습하는데 사용한 것과 동일한 목적을 복구할 수 있다.
한편 결정론적으로 토큰을 하나씩 Masking 하는 diffusion 프로세스에 대해 적절한 MASK 조건을 설정하면 KL 항이 Autoregressive 모델에 대한 표준 Cross-entropy 손실이 된다는 것을 보일 수 있다.
마지막으로 Masked Language Model은 Discrete 절차에 해당함을 보일 수 있다. 이미지 패치에 벡터 양자화를 적용한 후 이미지 도메인에서 적절한 절차를 사용하면 해당하는 병렬, 반복적인 디코더는 autoregressive 디코더 보다 훨씬 빠른다.

참고

Made with