•
Image Classification은 이미지를 보고 class를 분류하는 task
•
컴퓨터는 이미지를 픽셀 정보로 봄. 숫자를 보고 class를 맞춰야 함
•
같은 이미지지만 크기, 카메라 각도, 배경, 조명, 포즈에 따라 픽셀 값은 완전히 달라짐.
◦
사람은 그런게 바뀌어도 쉽게 인식 함
•
어떻게 이미지를 보고 class를 맞출 것인가?
•
logical 한 방법으로는 잘 안 됨
•
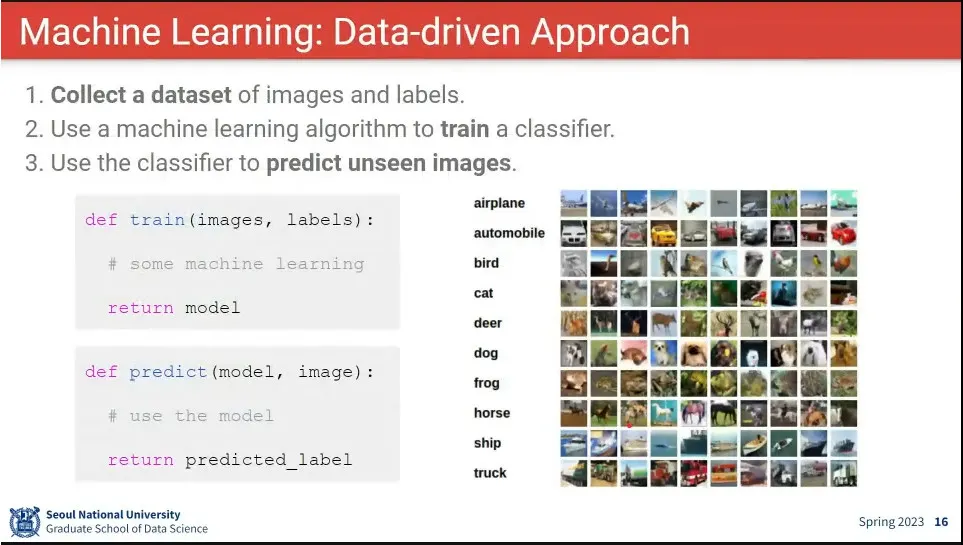
머신러닝은 Data-driven 접근 방법
◦
train과 predict를 구분하는게 주요함.
•
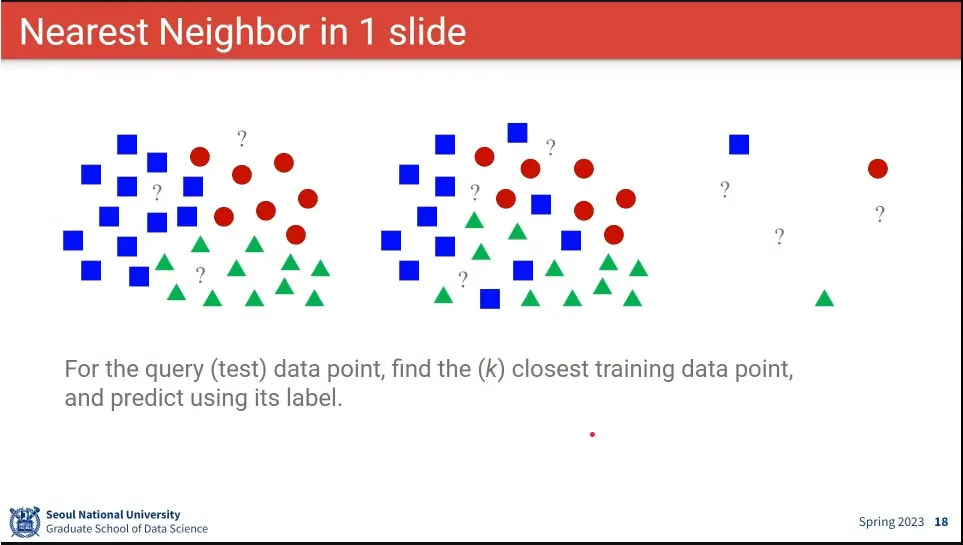
데이터가 어디에 가까운지를 보고 분류를 설정
•
Nearest Neighbor를 이용한 이미지 분류 방법
•
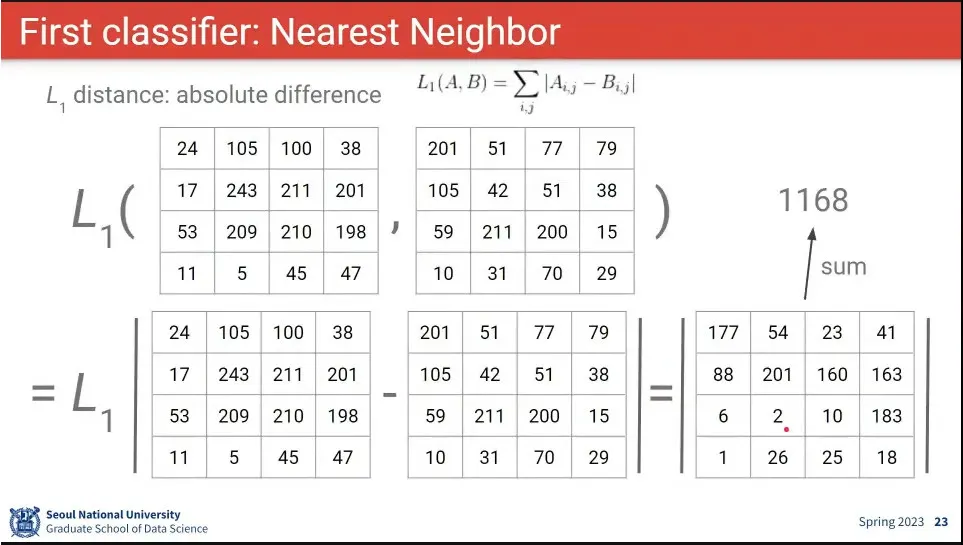
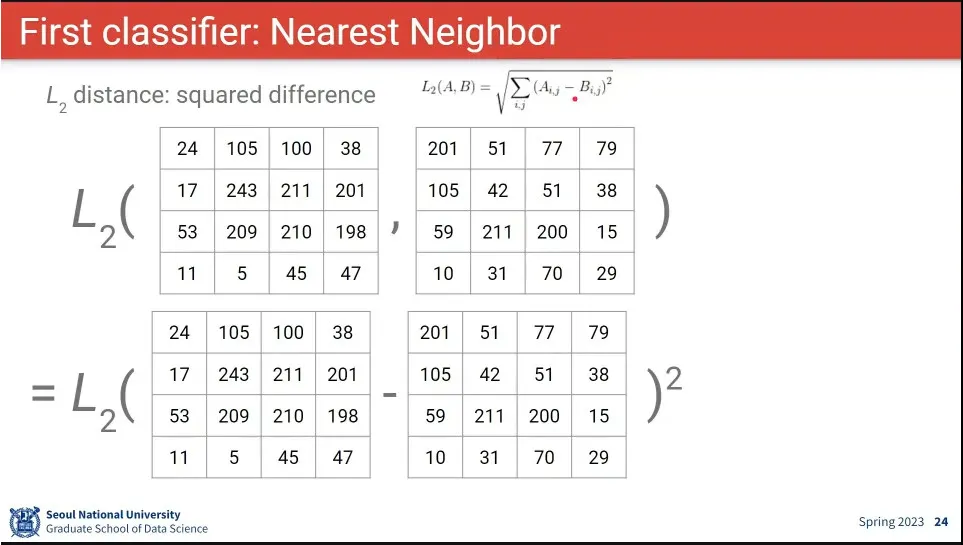
두 이미지의 Distance는 두 행렬 —엄밀히는 텐서— 의 Distance를 비교하는 것과 같음.
◦
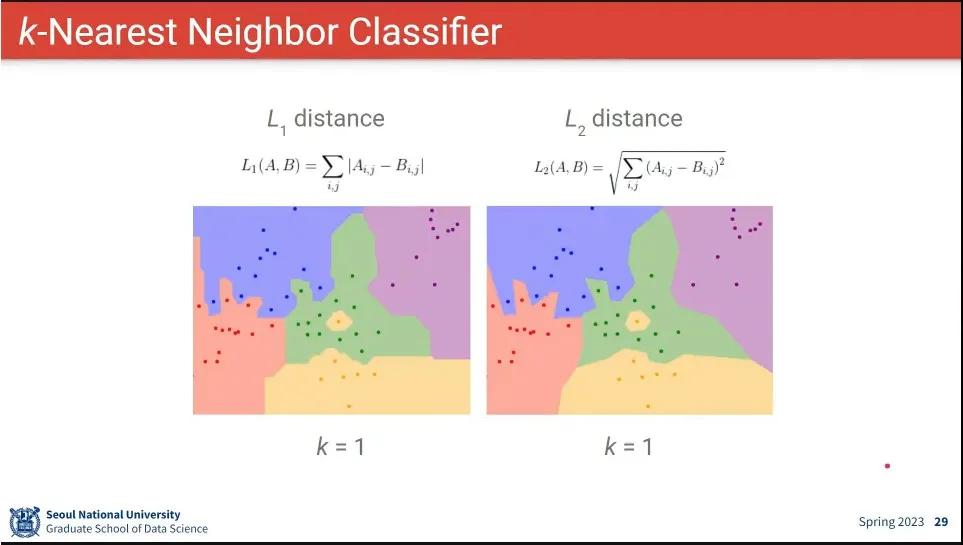
거리 비교는 절대값을 비교하는 L1 거리와 제곱을 비교하는 L2 거리가 있음
•
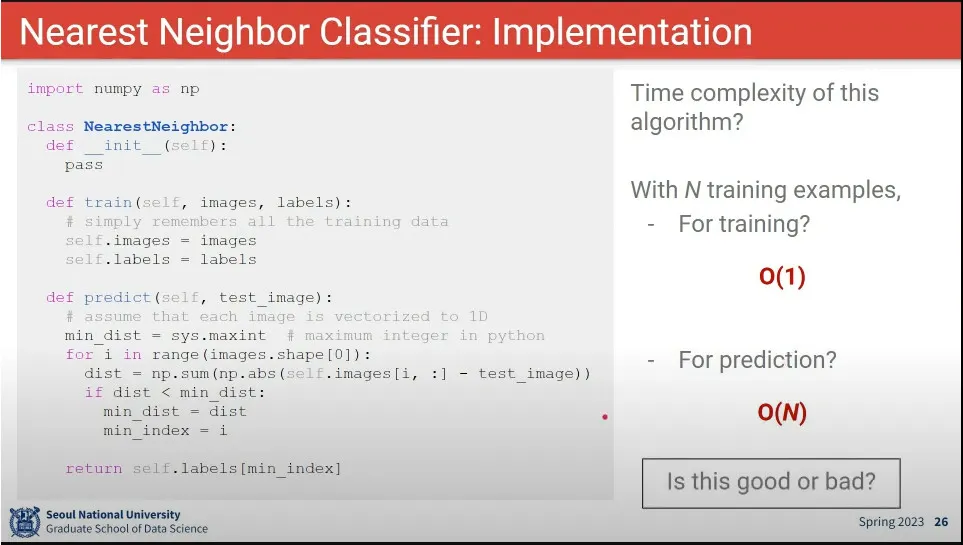
Nearest Neighbor 구현 코드 예시
•
Nearest Neighbor 의 시간 복잡도는 predict 할 때 더 오래 걸리기 때문에 좋지 않음
◦
training이 오래 걸리는 것은 큰 문제 없음. predict이 빨리 끝나야 좋은 알고리즘
•
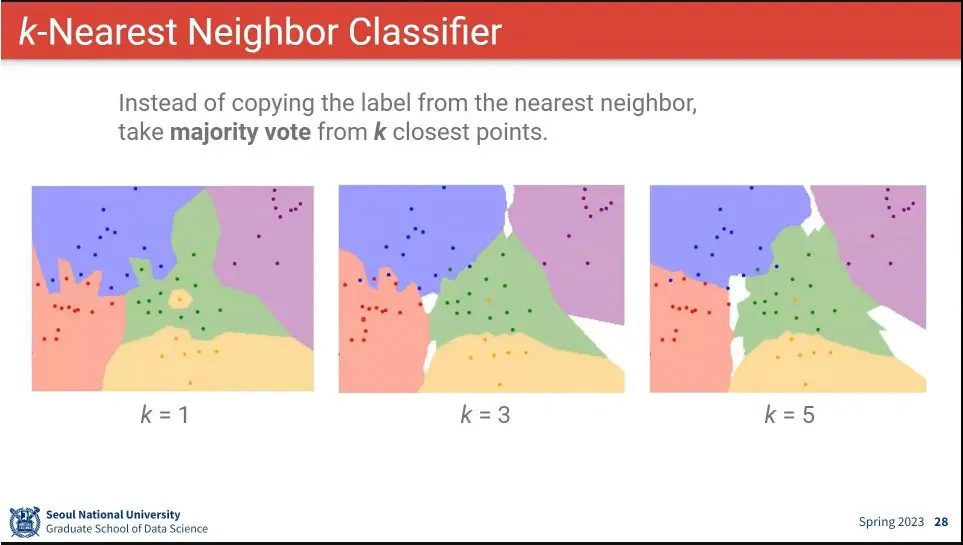
데이터에는 noise가 항상 존재하기 때문에, 그것을 보정하기 위해 k=1이 아니라 더 많은 값을 사용함.
•
L1, L2를 사용할 때는 큰 차이 없음.
•
하이퍼 파라미터를 고르는 방법은 별다른 방법이 없다. 그냥 이것저것 다 해보고 좋은 것을 고르는 것.
◦
일반적으로 파라미터라고 하면 모델이 배워야 하는 파라미터를 의미하고, 하이퍼 파라미터는 사람이 정해주는 값을 의미함.
•
Nearest Neighbor는 작은 변화에도 값이 크게 달라지기 때문에 좋은 방법이 아님.
•
Nearest Neighbor는 차원이 커짐에 따라 차원의 저주가 발생함.
•
Nearest Neighbor를 사용할 때 고려할 것들
◦
정규화, 차원축소, train/validation 구분, 근사 계산 등
•
parametric approach란 input을 어떤 label에 mapping 시키는 모델 함수를 이용하는 것
•
input에 대해 곱해지는 weight를 정의하고, 그 곱의 결과가 어떤 label에 mapping 되도록 w를 학습시킨다.
•
앞선 선형 곱을 함수로 쓰면 위와 같음
•
이미지의 크기를 3072(32x32x3)이라고 하고 최종 label의 수가 10개라고 할 때 W는 10 x 3072가 된다.
•
input과 weight의 곱에 학습에 보정을 추가하기 위해 bias를 추가하게 되는데, 이 경우 bias는 10x1의 크기가 됨.
•
bias를 매번 따로 추가해주는게 번거롭기 때문에, bias를 아예 추가한 식으로 표현 함.
•
이와 같은 방법을 사용하면 W만 저장하고, predict 단계에서 반복문 없이 행렬곱만 하면 되기 때문에, 공간적, 시간적으로 효율적임.
•
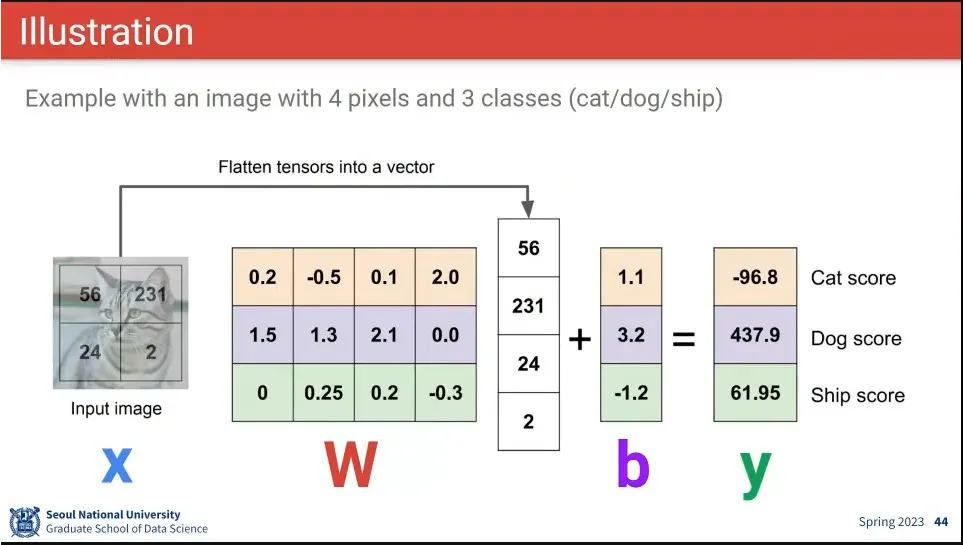
예시
◦
위 식에 따르면 W의 4번째 값이 크고 2번째 값이 작아야 고양이일 가능성이 높다. 1, 3번째 픽셀 값은 그다지 중요하지 않음.
◦
강아지일 경우 3번째 픽셀의 값이 중요하고, 1, 2번째 픽셀도 커야 함.
◦
bias에 dog의 값이 크다는 것은 데이터셋에 dog 샘플이 많았다는 것 등으로 해석 가능
•
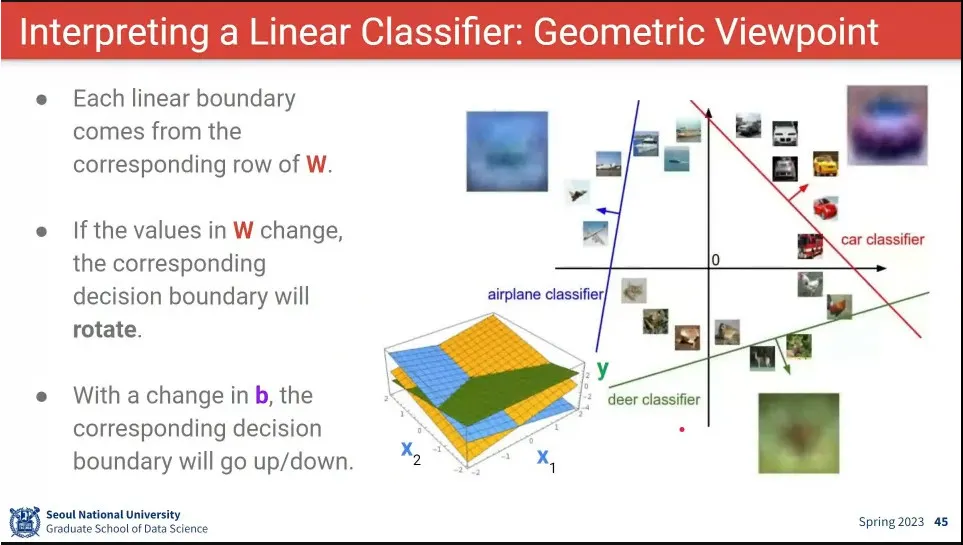
class를 기하학적으로 표현한 예
◦
아래 이미지에서 노란색 class는 x1, x2가 둘다 큰 것에 적합하고,
◦
파란색 class는 x1은 작고 x2는 클 수록 적합.
◦
녹색 class는 x1은 상관 없고 x2가 작은 게 중요해 짐
•
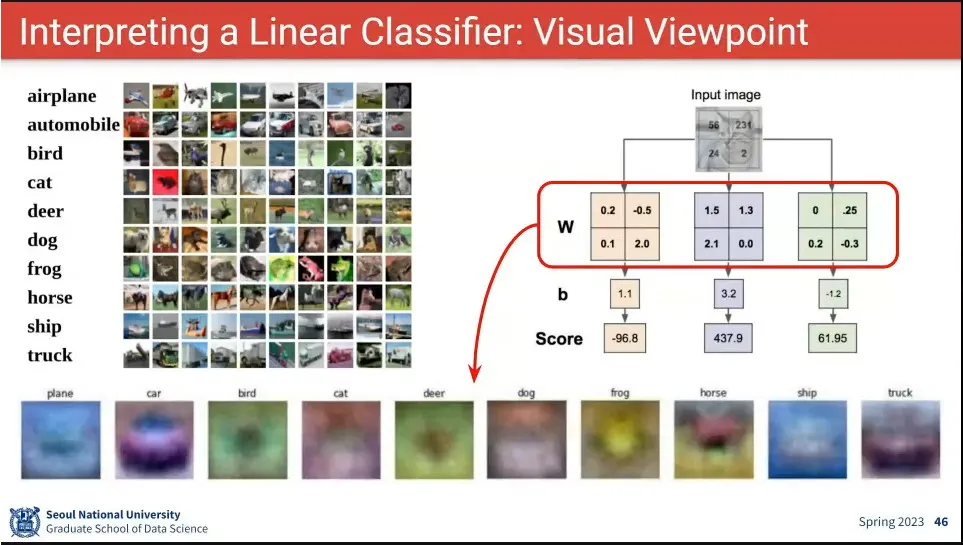
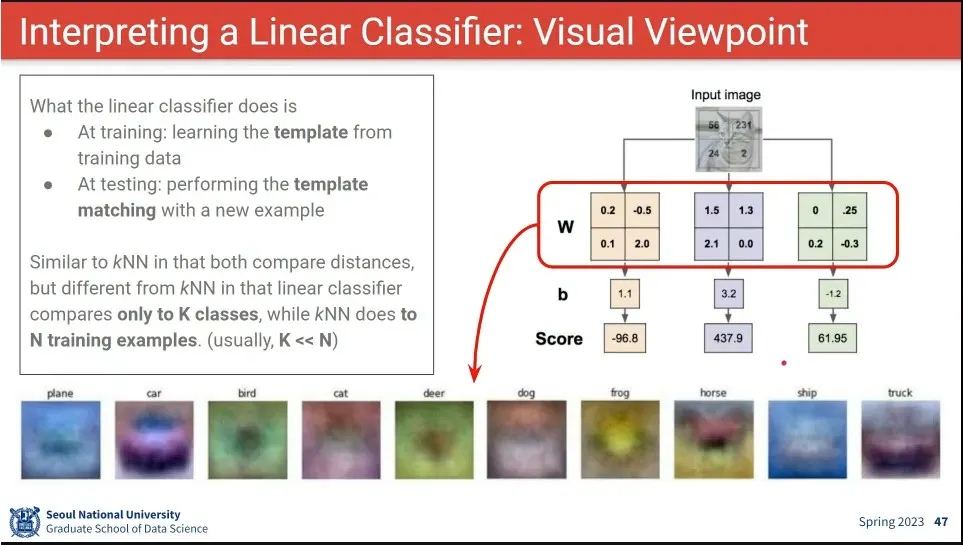
학습된 W를 이미지화 시킨 예
•
input에 대해 W를 곱하는 것은 학습된 W로 만든 각 이미지와 유사도를 찾는 것과 같다.