AI/ Paper/ Flash Attention

Transformer는 self-attention의 시간과 메모리 복잡도가 시퀀스 길이에 따라 2차적이기 때문에 긴 시퀀스에서 느리고 메모리가 부족하다. 근사 attention 방법은 모델 품질과 계산 복잡도의 trading off로 이 문제를 해결하려고 시도했지만 wall-clock 속도 향상을 달성하지 못했다. 우리는 attention 알고리즘을 IO-aware으로 만드는 것이 놓친 원칙라고 주장한다. 즉, GPU 메모리의 계층 사이에서 읽고 쓰기를 고려해야 한다. 우리는 IO-aware 정확한 attention 알고리즘인 FlashAttention을 제안한다. 이것은 타일링을 사용하여 GPU HBM(high bandwidth memory)과 GPU on-chip SRAM 사이의 메모리 읽기/쓰기의 수를 줄인다. 우리는 FlashAttention의 IO 복잡도를 분석하여 표준 attention과 비교에서 더 적은 HBM 접근만 필요하며, 이것이 일정 범위의 SRAM 크기 대해 최적임을 보인다. 또한 FlashAttention을 block-spare attention으로 확장하여 기존의 근사 attention 방법 보다 빠른 근사 attention 알고리즘을 산출한다. FlashAttention은 Transformer를 학습하는데 기존 baseline보다 더 빠르다. BERT-large(시퀀스 길이 512)에서 MLPerf 1.1 학습 속도 기록 대비 15% end-to-end wall-clock 속도 향상, GPT-2(시퀀스 길이 1K)에서 3배 빠르고, long-ragne arena(시퀀스 길이 1K-4K)에서 2.4배 빠르다. FlashAttention과 block-sparse FlashAttention은 transformer에서 더 긴 context를 허용하여 더 높은 품질 모델(GPT-2에서 0.7 낮은 perplexity와 긴 문서 분류에 대해 6.4점 향상)과 완전히 새로운 기능을 제공한다. 이것은 Path-X challenge(시퀀스 길이 16K, 61.4% 정확도)와 Path-256(시퀀스 길이 64K, 63.1% 정확도)에서 우연 수준 이상의 성능을 내는 최초의 transformer이다.

1 Introduction

Transformer 모델은 자연어 처리나 이미지 분류 같은 응용에서 가장 널리 사용되는 아키텍쳐로 등장했다. transformer는 더 커지고 더 깊어지고 있지만 그 핵심인 self-attention 모듈이 시퀀스 길이에 따라 계산 시간과 메모리 복잡도가 2차적이기 때문에 더 긴 context를 장착하는 것이 여전히 어렵다. 중요한 질문은 attention을 더 빠르고 더 메모리 효율적으로 만드는 것이 transformer가 긴 시퀀스에 대한 실행 시간과 메모리 도전을 해결하는데 도움이 될 수 있는지 여부이다.

많은 근사 attention 방법이 attention의 계산과 메모리 요구량을 줄이는데 초점을 맞추었다. 이러한 방법에는 sparse-approximation에서 low-rank approximation과 그들의 결합이 있다. 이런 방법들이 계산 요구량을 시퀀스 길이에 따라 선형이나 비선형으로 줄일 수 있지만, 그들 중 많은 것이 표준 attention과 비교하여 실제 성능 향상을 보이지 않았고 널리 채택되지 않았다. 주요한 이유는 그들이 FLOP 축소(실제 속도와 관련 없는)에만 초점을 맞추고 메모리 접근(IO)에서 오버헤드를 무시하는 경향을 갖기 때문이다.

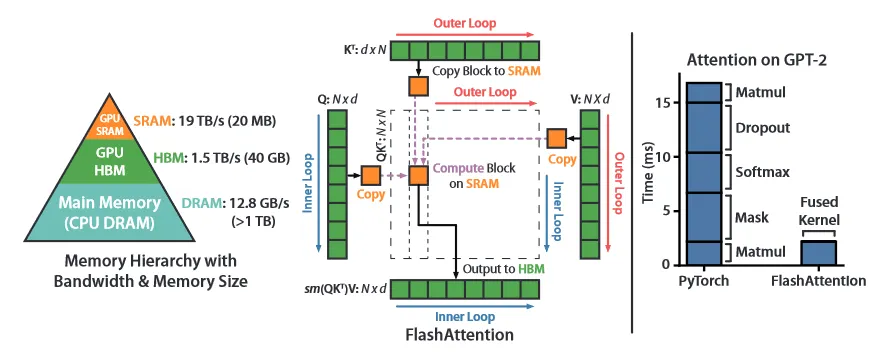
이 논문에서 우리는 놓친 원칙이 attention 알고리즘을 IO-aware로 만드는 것이라고 주장한다. 즉 빠르고 느린 메모리의 서로 다른 계층(빠른 GPU on-chip SRAM과 상대적으로 느린 GPU HBM. 그림 1 왼쪽)사이의 대한 읽기와 쓰기를 주의 깊게 고려해야 한다. 현대 GPU에서 계산 속도가 메모리 속도를 앞서고 있으며 Transformer에서 대부분의 연산은 메모리 접근에 의한 병목에서 발생한다.

IO-aware 알고리즘은 데이터 읽기와 쓰기가 실행 시간의 대부분을 차지할 수 있는 유사한 메모리-제한 연산에서 핵심이다. 예컨대 데이터베이스 join, 이미지 프로세싱, 수치적 선형 대수 등. 그러나 PyTorch나 Tensorflow 같은 python 딥러닝 인터페이스는 메모리 접근에 대한 미세 조정을 허용하지 않는다.

우리는 FlashAttention을 제안한다. 이것은 훨씬 더 적은 메모리 접근으로 정확한 attention을 계산하는 새로운 attention 알고리즘이다. 우리의 주요 목표는 HBM에서 attention 행렬을 읽고 쓰는 것을 피하는 것이다. 이를 위해 (i) 전체 입력에 접근하지 않고 softmax 축소를 계산하고 (ii) backward 패스에서 큰 중간 attention 행렬을 저장하지 않아야 한다. (1) 입력을 블록으로 나누고 입력 블록에 대해 여러 번 통과하여 점진적으로 softmax를 수행하도록 attention 연산을 재구성한다(tiling이라고 부름) (ii) backward pass에서 on-chip에서 빠르게 attention을 recomputation하기 위해 forward 패스에서 softmax normalization 계수를 저장한다. 이것은 HBM에서 중간 attention 행렬을 읽는 표준 접근에 비해 더 빠르다. 우리는 CUDA에서 FlashAttention을 구현하여 메모리 접근에 대한 미세 조정을 달성하고 모든 attention 연산을 하나의 GPU 커널로 융합한다. recomputation 때문에 FLOP이 증가함에도 우리 알고리즘은 표준 attention과 비교하여 실행이 더 빠르고(GPT-2에 대해 7.6배까지. 그림 1 오른쪽)과 메모리도 덜 사용한다. 이는 HBM 접근의 양을 줄인 덕분에 시퀀스 길이에서 선형이다.

우리는 또한 FlashAttention이 메모리 접근 오버헤드 이슈를 극복하여 근사 attention 알고리즘의 잠재적를 현실화 하는데 유용한 primitive가 될 수 있음을 보인다. PoC로써 우리는 block-sparse FlashAttention을 구현한다. sparse attention 알고리즘은 FlashAttention 보다도 2-4배 더 빠르고 64k 시퀀스 길이까지 확장될 수 있다. 우리는 block-sparse FlashAttention이 sparsity 비율에 비례하는 계수만큼 FlashAttention 보다 더 나은 IO 복잡도를 가짐을 증명한다. 우리는 섹션 5에서 다른 연산(Multi-GPU에 대한 attention, kernel regression, block-sparse 행렬 곱)에 대한 추가 확장을 논의한다. 우리는 이 primitive를 기반으로 구축하기 쉽도록 FlashAttention 오픈소스화한다.

우리는 FlashAttention이 모델 학습 속도를 높이고 더 긴 컨텍스트를 모델링하여 모델 품질을 개선할 수 있음을 경험적으로 검증한다. 또한 기존 attention 구현과 비교하여 FlashAttention과 block-sparse FlashAttention의 실행시간과 메모리 사용량을 벤치마크 한다.

•

Faster Model Training. FlashAttention은 Transformer 모델을 실제 시간으로 더 빠르게 학습시킨다. 우리는 BERT-large(시퀀스 길이 512)를 MLPerf 1.1의 학습 속도 기록보다 15% 더 빠르게 학습하고, GPT2(시퀀스 길이 1K)를 HuggingFace와 Megatron-LM의 baseline 구현보다 3배 더 빠르게, long-range arena(시퀀스 길이 1K-4K)를 baseline보다 2.4배 더 빠르게 학습시킨다.

•

Higher Quality Models. FlashAttention은 Transformer를 더 긴 시퀀스로 확장하여 품질을 개선하고 새로운 수용량을 허용한다. 우리는 GPT-2에서 0.7의 perpelxity 개선과 긴 문서 분류에서 더 긴 시퀀스 모델링으로 6.4점을 끌어 올렸다. FlashAttention은 더 긴 시퀀스 길이(16K)를 사용하는 것만으로 Path-X 챌린지에서 우연 수준 이상의 성능을 달성한 최초의 transformer 모델이다. Block-sprase FlashAttention은 Transformer를 더 긴 시퀀스(64K)로 확장하여 Path-256에서 우연 수준 이상의 성능을 달성한 첫 번째 모델이다.

•

Benchmarking Attention. FlashAttention은 일반적인 시퀀스 길이 128에서 2K의 표준 attention 구현 보다 3배 더 빠르고 64K까지 확장된다. 시퀀스 길이 512까지 FlashAttention은 기존 attention 방법 보다 더 빠르고 메모리 효율적이다. 반면 1K를 넘어선 시퀀스 길이에 대해 일부 근사 attention 방법(예: Linformer)는 더 빨라지기 시작한다. 반면 block-sparse FlashAttention은 우리가 아는 기존의 모든 근사 attention 방법보다 더 빠르다.

2 Background

우리는 현대 하드웨어(GPUs)에 대한 일반적인 딥러닝 연산의 성능 특성에 대한 배경을 제공한다. 우리는 또한 attention의 표준 구현을 설명한다.

2.1 Hardware Performance

여기서 GPUs에 초점을 맞춘다. 다른 하드웨어 가속기의 성능도 유사하다.

GPU Memory Hierarchy.

GPU 메모리 계층구조(그림 1 왼쪽)은 다양한 크기와 속도의 여러 형태의 메모리로 구성되며, 메모리가 작을수록 더 빠르다. 예컨대 A100 GPU는 초당 1.5-2.0TB의 bandwidth를 갖는 40-80GB의 HBM과 초당 약 19TB의 bandwidth를 갖는 108개의 streaming multiprocess 각각 192KB의 on-chip SRAM을 갖는다. on-chip SRAM은 HBM 보다 훨씬 빠르지만 크기는 훨씬 더 작다. 메모리 속도에 비해 컴퓨팅 속도가 빨라지면서 메모리(HBM) 접근에 의한 병목이 점점 더 발생하고 있다. 따라서 빠른 SRAM이 활용하는 것이 더욱 중요하다.

Execution Model.

GPUs는 계산을 실행하기 위해 엄청난 수의 thread(커널이라 부르는)를 갖는다. 각 커널은 HBM에서 입력을 레지스터와 SRAM에 로드하고, 계산한 다음 다시 출력을 HBM에 쓴다.

Performance characteristics.

계산과 메모리 접근의 균형에 따라 연산은 compute-bound 또는 memory-bound로 분류될 수 있다. 이것은 일반적으로 메모리 접근의 바이트 당 산술 연산의 수인 산술 강도(arithmetic intensity)로 측정된다.

Compute-bound: 연산에 소요되는 시간은 산술 연산의 수에 따라 결정되는 반면 HBM에 접근하는 시간은 훨씬 적다. 일반적인 예로 내부 차원이 큰 행렬 곱과 채널 수가 많은 convolution이 있다.

Mermoy-bound: 연산에 소요되는 시간은 메모리 접근의 수에 의해 결정되지만 계산에서 소요되는 시간은 훨씬 더 적다. 예로는 elementwise(예: activation, dropout)과 reduction(예: sum, softmax, batch norm, layer norm) 등의 대부분의 다른 작업이 포함된다.

Kernel fusion.

memory-bound 연산을 가속하는 가장 일반적인 접근은 kernel fusion이다. 동일한 입력에 대해 여러 연산이 적용된는 경우 각 연산에 대해 입력을 여러 번 로드하는 대신 HBM에서 한 번에 로드 할 수 있다. 컴파일러는 많은 elementwise 연산을 자동으로 융합할 수 있다. 그러나 모델 학습의 맥락에서 backward 패스를 위해 여전히 중간 값을 HBM에 저장해야 한다. 이것은 naive kernel fusion의 효율성을 줄인다.

2.2 Standard Attention Implementation

입력 시퀀스

\bold{Q}, \bold{K}, \bold{V} \in \mathbb{R}^{N\times d}

(여기서

N

은 시퀀스 길이이고

d

는 head 차원)가 주어질 때, 우리는 attention 출력

\bold{O} \in \mathbb{R}^{N \times d}

를 계산하기를 원한다.

\begin{aligned} \bold{S} &= \bold{QK}^\top \in \mathbb{R}^{N \times N} \\ \bold{P} &= \text{softmax}(\bold{S}) \in \mathbb{R}^{N \times N} \\ \bold{O} &= \bold{PV} \in \mathbb{R}^{N \times d} \end{aligned}

여기서 softmax는 row-wise로 적용된다.

표준 attention 구현은 행렬

\bold{S}

와

\bold{P}

를 HBM에 구현하므로

O(N^2)

메모리가 필요하다. 종종

N \gg d

이다. (예: GPT-2의 경우

N=1024

이고

d=64

). Algorithm 0에서 표준 attention 구현을 설명한다. 일부 또는 대부분의 연산이 memory-bound(예: softmax)이고 메모리 접근이 느린 실제 시간으로 이어진다.

이 문제는

\bold{S}

에 적용된 masking이나

\bold{P}

에 적용된 dropout 같이 attention 행렬에 적용되는 다른 elementwise 연산에 의해 더 악화된다. 결과적으로 masking과 softmax를 융합하는 것과 같이 elementwise 연산을 융합하려는 많은 시도가 있었다.

섹션 3.2에서 표준 attention 구현이 시퀀스 길이

N

에 따라 2차적으로 HBM에 접근하는 것을 보인다. 또한 표준 attention과 우리의 방법(FlashAttention)의 FLOP 수와 HBM 접근 수를 비교한다.

Algorithm 0. Standard Attention 구현

Require: HBM에 행렬

\bold{Q}, \bold{K}, \bold{V} \in \mathbb{R}^{N\times d}

HBM에서 block 별로 Q,K\bold{Q}, \bold{K}Q,K를 로드, S=QK⊤\bold{S} = \bold{QK}^\topS=QK⊤를 계산, S\bold{S}S를 HBM에 씀

HBM에서 S\bold{S}S를 읽고, P=softmax(S)\bold{P} = \text{softmax}(\bold{S})P=softmax(S)를 계산, P\bold{P}P를 HBM에 씀

HBM에서 block 별로 P\bold{P}P와 V\bold{V}V를 로드, O=PV\bold{O} = \bold{PV}O=PV를 계산 O\bold{O}O를 HBM에 씀

O\bold{O}O 반환

3 FlashAttention: Algorithm, Analysis, and Extensions

우리는 HBM 읽기/쓰기를 줄이고 backward 패스에 대한 큰 중간 행렬을 저장하지 않고 정확한 attention을 계산하는 방법을 보인다. 이를 통해 메모리 효율적이고 실제 시간에서 더 빠른 attention 알고리즘을 산출한다. 우리는 그 IO 복잡성을 분석하여 우리의 방법이 표준 attention과 비교하여 훨씬 더 적은 HBM 접근을 요구함을 보인다. 나아가 FlashAttention이 block-sparse attention을 다루도록 확장하여 유용한 primitive가 될 수 있음을 보인다.

여기서 설명을 용이를 위해 forward pass에 초점을 맞춘다. 부록 B에서 backward의 상세 내용을 다룬다.

3.1 An Efficient Attention Algorithm With Tiling and Recomputation

HBM에서 입력

\bold{Q}, \bold{K}, \bold{V} \in \mathbb{R}^{N\times d}

이 주어지면, 우리는 attention 출력

\bold{O}\in \mathbb{R}^{N\times d}

를 계산하고 HBM에 쓰는 것에 초점을 맞춘다. 우리의 목표는 HBM 접근의 양을 줄이는 것이다.(

N

에 sub-quadratic)

우리는 2가지 기법(tiling, recomputation)을 설립하여 sub-quadratic HBM 접근에서 정확한 attention을 계산하는 기술적 도전을 극복한다. 우리는 이것을 Algorithm 1에서 설명한다. 주요 아이디어는 입력

\bold{Q}, \bold{K}, \bold{V}

을 block으로 분할하고, 느린 HBM에서 빠른 SRAM으로 로드한 다음 이 블록 측면에서 attention 출력을 계산하는 것이다. 각 블록의 출력을 합산하기 전에 올바른 정규화 계수로 scaling하면 마지막에 올바른 결과를 얻을 수 있다.

Tiling.

우리는 attention을 block 별로 계산한다. softmax는

\bold{K}

의 열을 커플링하므로 scaling을 통해 큰 softmax를 분해한다. 수치적 안정성을 위해 벡터

x \in \mathbb{R}^B

의 softmax는 다음과 같이 계산된다.

\begin{aligned} m(x) &:= \max_i x_i \\ f(x) &:= [e^{x_1-m(x) } \quad ... \quad e^{x_B - m(x)}] \\ \ell(x) &:= \sum_i f(x)_i \\ \text{softmax}(x) &:= {f(x) \over \ell(x)} \end{aligned}

벡터

x^{(1)}, x^{(2)} \in \mathbb{R}^B

에 대해 다음과 같이 concatenated 된

x = [x^{(1)} \quad x^{(2)}] \in \mathbb{R}^{2B}

의 softmax를 다음과 같이 분해할 수 있다.

\begin{aligned} m(x) &= m( [x^{(1)} \quad x^{(2)}]) = \max(m(x^{(1)}), m(x^{(2)})) \\ f(x) &= [e^{m(x^{(1)}) - m(x)}f(x^{(1)}) \quad e^{m(x^{(2)})-m(x)}f(x^{(2)}) ] \\ \ell(x) &= \ell([x^{(1)} \quad x^{(2)}]) = e^{m(x^{(1)})-m(x)}\ell(x^{(1)}) + e^{m(x^{(2)}) - m(x)}\ell(x^{(2)}) \\ \text{softmax}(x) &= {f(x) \over\ell(x)}\end{aligned}

f(x) := [e^{x_1-m(x) } \quad ... \quad e^{x_B - m(x)}]

라 할 때

x = [x^{(1)} \quad x^{(2)}] \in \mathbb{R}^{2B}

이고

x^{(1)}, x^{(2)} \in \mathbb{R}^B

에 대해 위의 식을

f(x) = [e^{m(x^{(1)}) - m(x)}f(x^{(1)}) \quad e^{m(x^{(2)})-m(x)}f(x^{(2)}) ]

는 다음과 같이 유도된다. (여기서

f(x^{(1)}), f(x^{(2)})

는 스칼라) 우선

x^{(1)} \in \mathbb{R}^B

을 보면 (편의상

e^x

를

\exp(x)

로 표기)

\begin{aligned} \exp(x_1 - m(x)) &= \exp(m(x^{(1)}) - m(x))f(x^{(1)}) \\ &= \exp(m(x^{(1)}) - m(x))\exp(x_1^{(1)}-m(x^{(1)}) \\ &= \exp(m(x^{(1)})-m(x) + x_1^{(1)} - m(x^{(1)})) \\ &= \exp(x_1^{(1)}-m(x))\end{aligned}

x^{(2)} \in \mathbb{R}^B

에 대해서도 동일하게 유도하면

\exp(x_2 - m(x)) = \exp(x_2^{(2)}-m(x))

가 된다.

\ell(x) := \sum_i f(x)_i

에 대해

i=2

이면

f(x)_1 + f(x)_2 = \exp(x_1-m(x)) + \exp(x_2 - m(x))

가 된다. 이를 이용하여

\ell(x) = e^{m(x^{(1)})-m(x)}\ell(x^{(1)}) + e^{m(x^{(2)}) - m(x)}\ell(x^{(2)})

에 대해(여기서

\ell(x^{(1)}), \ell(x^{(2)})

는 스칼라) 1번째 항목에 대해 위와 같은 식으로 정리하면

\begin{aligned} \exp(x_1 - m(x)) &= \exp(m(x^{(1)}) - m(x))\ell(x^{(1)}) \\ &= \exp(m(x^{(1)}) - m(x))\exp(x_1^{(1)}-m(x^{(1)}) \\ &= \exp(m(x^{(1)})-m(x) + x_1^{(1)} - m(x^{(1)})) \\ &= \exp(x_1^{(1)}-m(x))\end{aligned}

x^{(2)} \in \mathbb{R}^B

에 대해서도 동일하게 유도하면

\exp(x_2 - m(x)) = \exp(x_2^{(2)}-m(x))

가 되고 최종

\ell(x) = \exp(x_1^{(1)} - m(x)) + \exp(x_2^{(2)} - m(x))

가 된다.

따라서 몇 가지 추가 통계량

(m(x), \ell(x))

을 추적하면 한 번에 한 블록씩 softmax를 계산할 수 있다. 따라서 입력

\bold{Q}, \bold{K}, \bold{V}

를 블록으로 분할하고(Algorithm 1의 3번째 줄), 추가 통계량과 함께 softmax 값을 계산하고(Algorithm 1의 10번째 줄), 결과를 결합한다(Algorithm 1의 12번째 줄)

Recomputation.

우리 목표 중 하나는 backward 패스에 대해

O(N^2)

중간 값을 저장하지 않 것이다. 일반적으로 backward 패스는

\bold{Q}, \bold{K}, \bold{V}

에 대한 gradient를 계산하기 위해 행렬

\bold{S}, \bold{P} \in \mathbb{R}^{N \times N}

이 필요하다. 그러나 출력

\bold{O}

와 softmax 정규화 통계량

(m, \ell)

을 저장하면 backward 패스에서 SRAM의

\bold{Q}, \bold{K}, \bold{V}

블록에서 attention 행렬

\bold{S}

와

\bold{P}

를 쉽게 recompute 할 수 있다. 이것은 selective gradient checkpointing의 형식으로 볼 수 있다. gradient checkpointing은 최대 메모리 요구량을 줄이기 위해 제안되었지만, 우리가 아는 한 모든 구현에서 속도와 메모리를 trade off 해야 한다. 반면 우리의 recomputation은 FLOPs가 더 많아지더라도 HBM 접근을 줄이기 때문에(그림 2) backward pass의 속도를 높인다. 전체 backward pass는 부록 B에 설명된다.

Implementation details: Kernel fusion.

Tiling을 통해 우리의 알고리즘을 하나의 CUDA 커널로 구현할 수 있다. HBM에서 입력을 로드하고, 모든 계산 단계(행렬 곱, softmax, optionally masking과 dropout, 행렬 곱)를 수행하고, 그 다음 HBM으로 결과를 다시 쓴다(부록 B의 masking과 dropout). 이를 통해 HBM에서 입력과 출력을 반복적으로 읽고 쓰는 것을 피할 수 있다.

Algorithm 1 FlashAttention

Require: HBM에서 행렬

\bold{Q}, \bold{K}, \bold{V} \in \mathbb{R}^{N\times d}

, 크기

M

의 on-chip SRAM

블록 크기 설정 Bc=⌈M4d⌉,Br=min⁡(⌈M4d⌉,d)B_c = \lceil{M \over 4d} \rceil, B_r = \min(\lceil{M \over 4d}\rceil, d)Bc​=⌈4dM​⌉,Br​=min(⌈4dM​⌉,d)

HBM에서 초기화 O=(0)N×d∈RN×d,ℓ=(0)N∈RN,m=(−∞)N∈RN\bold{O} = (0)_{N \times d} \in \mathbb{R}^{N \times d}, \ell = (0)_N \in \mathbb{R}^N, m = (-\infty)_N \in \mathbb{R}^NO=(0)N×d​∈RN×d,ℓ=(0)N​∈RN,m=(−∞)N​∈RN

Q\bold{Q}Q를 각각 Br×dB_r \times dBr​×d 크기의 Tr=⌈NBr⌉T_r = \lceil{N \over B_r}\rceilTr​=⌈Br​N​⌉개 블록 Q1,...,QT\bold{Q}_1, ..., \bold{Q}_TQ1​,...,QT​으로 분할하고 K,V\bold{K}, \bold{V}K,V를 각각 Bc×dB_c \times dBc​×d 크기의 Tc=⌈NBc⌉T_c = \lceil{N \over B_c}\rceilTc​=⌈Bc​N​⌉개 블록 K1,...,KTc\bold{K}_1, ..., \bold{K}_{T_c}K1​,...,KTc​​와  V1,...,VTc\bold{V}_1, ..., \bold{V}_{T_c}V1​,...,VTc​​으로 분할 

O\bold{O}O를 각각 Br×dB_r \times dBr​×d 크기의 TrT_r Tr​개 블록 Oi,...,OTr\bold{O}_i, ... , \bold{O}_{T_r}Oi​,...,OTr​​으로 분할, ℓ\ellℓ을 각각 BrB_rBr​ 크기의 TrT_rTr​개 블록 ℓi,...,ℓTr\ell_i, ..., \ell_{T_r}ℓi​,...,ℓTr​​으로 분할, mmm을 각각 BrB_rBr​ 크기의 TrT_rTr​개 블록 m1,...,mTrm_1, ..., m_{T_r}m1​,...,mTr​​으로 분할 

for 1≤j≤Tc1 \le j \le T_c1≤j≤Tc​ do

HBM에서 on-chip SRAM으로 Kj,Vj\bold{K}_j, \bold{V}_jKj​,Vj​를 로드

for 1≤i≤Tr1 \le i \le T_r1≤i≤Tr​ do

HBM에서 on-chip SRAM으로 Qi,Oi,ℓi,mi\bold{Q}_i, \bold{O}_i, \ell_i, m_iQi​,Oi​,ℓi​,mi​를 로드

ii.

on chip에서 다음을 계산

•

Sij=QiKj⊤∈RBr×Bc\bold{S}_{ij} = \bold{Q}_i\bold{K}_j^\top \in \mathbb{R}^{B_r \times B_c}Sij​=Qi​Kj⊤​∈RBr​×Bc​ 

◦

QK⊤\bold{QK}^\topQK⊤을 block으로 분할해서 계산

iii.

on chip에서 다음을 계산

•

m~ij=rowmax(Sij)∈RBr\tilde{m}_{ij} = \text{rowmax}(\bold{S}_{ij}) \in \mathbb{R}^{B_r}m~ij​=rowmax(Sij​)∈RBr​

◦

Sij\bold{S}_{ij}Sij​에서 수치적 안정성을 위한 근사 max 값 근사치를 계산

•

P~ij=exp⁡(Sij−m~ij)∈RBr×Bc(pointwise) \tilde{\bold{P}}_{ij} = \exp(\bold{S}_{ij} - \tilde{m}_{ij}) \in \mathbb{R}^{B_r \times B_c} (\text{pointwise})P~ij​=exp(Sij​−m~ij​)∈RBr​×Bc​(pointwise)

◦

원래 P\bold{P}P는 S\bold{S}S에 대해 softmax를 계산해야 하지만, 근사치로 분자 부분만 계산한다. 수치적 안정성을 위해 max 값을 빼서 계산

•

ℓ~ij=rowsum(P~ij)∈RBr \tilde{\ell}_{ij} = \text{rowsum}(\tilde{\bold{P}}_{ij}) \in \mathbb{R}^{B_r}ℓ~ij​=rowsum(P~ij​)∈RBr​

◦

P~ij\tilde{\bold{P}}_{ij}P~ij​를 합산하여 정규화 상수의 근사치 ℓ~ij\tilde{\ell}_{ij}ℓ~ij​를 구한다.

iv.

on chip에서 다음을 계산

•

minew=max⁡(mi,m~ij)∈RBrm_i^\text{new} = \max(m_i, \tilde{m}_{ij}) \in \mathbb{R}^{B_r}minew​=max(mi​,m~ij​)∈RBr​

◦

기존 max 보다 현재 반복문에서 구한 max를 비교해서 minewm_i^\text{new}minew​ 업데이트

•

ℓinew=emi−minewℓi+em~ij−minewℓ~ij∈RBr\ell_i^\text{new} = e^{m_i - m_i^\text{new}}\ell_i + e^{\tilde{m}_{ij} - m_i^\text{new}}\tilde{\ell}_{ij} \in \mathbb{R}^{B_r}ℓinew​=emi​−minew​ℓi​+em~ij​−minew​ℓ~ij​∈RBr​

◦

기존 정규화 상수 ℓi\ell_iℓi​에 현재 근사치 ℓ~ij\tilde{\ell}_{ij}ℓ~ij​를 더해서 ℓinew\ell_i^\text{new}ℓinew​ 업데이트. 여기서 exp⁡(mi−minew)\exp(m_i - m_i^\text{new})exp(mi​−minew​)와 exp⁡(m~ij−minew)\exp(\tilde{m}_{ij} - m_i^\text{new})exp(m~ij​−minew​)는 두 값의 비중을 조절하는 역할을 한다. max를 빼는 이유는 지수 합을 계산할 때 수치적 안정성을 위해 max값을 빼는 방법을 차용하는 것. ea+eb=emax⁡(a,b)(ea−max⁡(a,b)+eb−max⁡(a,b))e^a + e^b = e^{\max({a,b})}(e^{a-\max(a,b)} + e^{b-\max(a,b)})ea+eb=emax(a,b)(ea−max(a,b)+eb−max(a,b))

◦

minewm_i^\text{new}minew​이 항상 최대값이므로 mi−minewm_i - m_i^\text{new}mi​−minew​나 m~ij−minew\tilde{m}_{ij} - m_i^\text{new}m~ij​−minew​는 항상 0이하의 값이 된다. 0이면 해당 항의 비중은 1이 되고, minewm_i^\text{new}minew​와의 차이가 큰 음수가 될 수록 해당 항의 비중은 0에 가까워지게 됨.

HBM으로 Oi←diag(ℓinew)−1(diag(ℓi)emi−minewOi+em~ij−minewP~ijVj)\bold{O}_i \leftarrow \text{diag}(\ell_i^\text{new})^{-1}(\text{diag}(\ell_i)e^{m_i-m_i^\text{new}}\bold{O}_i + e^{\tilde{m}_{ij} - m_i^\text{new}}\tilde{\bold{P}}_{ij}\bold{V}_j)Oi​←diag(ℓinew​)−1(diag(ℓi​)emi​−minew​Oi​+em~ij​−minew​P~ij​Vj​) 쓰기

•

원래 O\bold{O}O는 PV\bold{PV}PV의 곱으로 표현되지만 block로 나눠서 처리하기 때문에 각 분할된 값을 기존 값에 더하는 식으로 업데이트한다. 이때 ℓinew\ell_i^\text{new}ℓinew​을 업데이트할 때와 마찬가지로 기존 값 O\bold{O}O와 새로 추가되는 값 P~ijVj\tilde{\bold{P}}_{ij}\bold{V}_jP~ij​Vj​에 대해 exp⁡(mi−minew)\exp(m_i - m_i^\text{new})exp(mi​−minew​)와 exp⁡(m~ij−minew)\exp(\tilde{m}_{ij} - m_i^\text{new})exp(m~ij​−minew​)를 이용해서 비중 조절함

•

기존 값 O\bold{O}O에 기존 정규화 상수를 곱하는 이유는 수치 안정성을 위함

•

기존 값과 새로운 값을 더한 전체 합에 대해 최종적으로 업데이트된 정규화 상수로 나눈다. diag(ℓinew)−1\text{diag}(\ell_i^\text{new})^{-1}diag(ℓinew​)−1 (대각의 역행렬(역수)을 곱함)

vi.

HBM으로 ℓi←ℓinew,mi←minew\ell_i \leftarrow \ell_i^\text{new}, m_i \leftarrow m_i^\text{new}ℓi​←ℓinew​,mi​←minew​ 쓰기

end for

end for

O\bold{O}O 반환

우리는 FlashAttention의 정확성, 실행 시간과 메모리 요구 사항을 부록 C에서 증명한다.

Theorem 1.

Algorithm 1은

O(N^2d)

FLOPs을 사용하여

\bold{O} = \text{softmax}(\bold{QK}^\top)\bold{V}

를 반환하고, 입력과 출력 외에

O(N)

의 추가 메모리가 필요하다.

3.2 Analysis: IO Complexity of FlashAttention

우리는 FlashAttention의 IO 복잡도를 분석하여 표준 attention과 비교하여 HBM 접근이 크게 감소한 것을 보인다. 우리는 또한 모든 SRAM 크기에 대해 HBM 접근을 점근적으로 개선할 수 있는 정확한 attention 알고리즘이 없다는 것을 증명하는 lower bound를 제공한다. 증명은 부록 C 참조.

Theorem 2.

N

을 시퀀스 길이,

d

를 head 차원,

\bold{M}

을 SRAM의 크기라고 하고

d \le M \le Nd

라 하자. 표준 attention (Algorithm 0)은

\Theta(Nd + N^2)

HBM 접근이 필요한 반면 FlashAttention(Algorithm 1)은

\Theta(N^2d^2M^{-1})

접근이 필요하다.

d

(64-128)와

M

(약 100KB)의 일반적인 크기에 대해

d^2

은

M

보다 몇 배 더 작으므로 FlashAttention은 표준 구현에 비해 몇 배 더 적은 HBM 접근만 요구한다. 이것은 섹션 4.3에서 검증한 더 빠른 실행과 더 적은 메모리 공간으로 이어진다.

증명의 주요 아이디어는 SRAM의 크기가

M

으로 주어질 때 각각

\Theta(M)

크기의

\bold{K}, \bold{V}

의 블록을 로드할 수 있다는 것이다(Algorithm 1의 6번째 줄).

\bold{K}

와

\bold{V}

의 각 블록에 대해 중간값을 계산하기 위해

\bold{Q}

의 모든 블록을 반복한다(Algorithm 1의 8번째 줄). 이로 인해

\bold{Q}

에 대해

\Theta(NdM^{-1})

의 패스가 발생한다. 각 패스에서

\Theta(Nd)

요소를 로드하므로 총

\Theta(N^2d^2M^{-1})

의 HBM 접근이 필요하다. 유사하게 표준 Attention의 backward 패스가 HBM 접근에

\Theta(Nd + N^2)

을 요구하는 반면 FlashAttention의 backward 패스는

\Theta(N^2d^2M^{-1})

의 HBM 접근을 요구한다. (부록 B 참조)

우리는 하한을 증명한다. 정확한 attention을 계산할 때

M

(SRAM 크기)의 모든 값에 대한 HBM 접근 수를 점근적으로 개선할 수 없다.

Proposition 3.

N

을 시퀀스 길이,

d

를 head 차원,

\bold{M}

을 SRAM의 크기라고 하고

d \le M \le Nd

라 하자. 범위

[d, Nd]

내에서 모든

M

에 대해

O(N^2d^2M^{-1})

의 HBM 접근을 사용하는 정확한 attention 계산 알고리즘은 존재하지 않는다.

증명은

M = \Theta(Nd)

에 대해 모든 알고리즘이

\Omega(N^2d^2M^{-1}) = \Omega(Nd)

의 HBM 접근을 수행해야 한다는 사실에 의존한다.

M

의 subrange에 대한 이러한 유형의 하한은 streaming 알고리즘 문헌에서 일반적이다. 우리는

M

에 대한 파라미터화된 복잡성 하한 증명을 흥미로운 향후 과제로 남긴다.

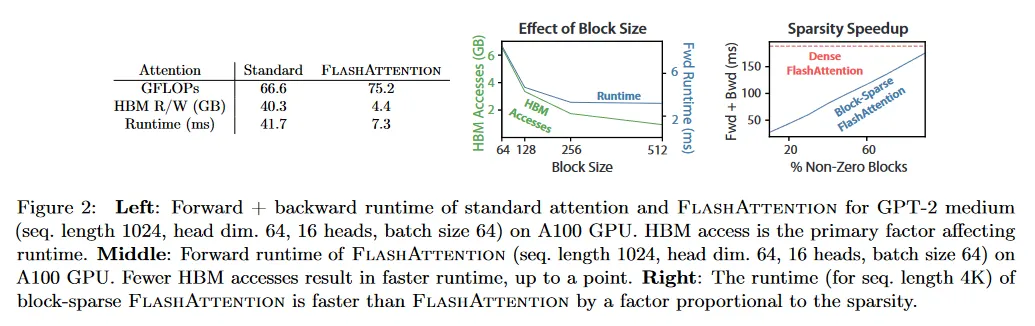
HBM 접근의 수가 attention runtime의 주요 결정 요인임을 검증한다. 그림 2(왼쪽)에서 FlashAttention이 표준 attention과 비교하여 더 높은 FLOP 수를 가짐에도(backward pass에서 recomputation 때문에), HBM 접근이 훨씬 적어서 실행 시간이 크게 단축되는 것을 볼 수 있다. 그림 2(중간)에서 우리는 FlashAttention의 블록 크기

B_c

를 변경하여 HBM 접근의 수를 다르게 하고 forward 패스의 실행 시간을 측정한다. 블록 크기가 증가함에 따라 HBM 접근의 수가 감소하고(입력에 대한 pass가 줄어듦), 실행시간도 감소한다. 블록 크기가 충분히 크면(256을 넘어) 실행 시간은 다른 요인들(예: 산술 연산)에 의해 병목이 발생한다. 또한 큰 블록 크기는 작은 SRAM 크기에 맞지 않다.

3.3 Extension: Block-Sparse FlashAttention

우리는 FlashAttention을 근사 attention으로 확장한다. 우리는 block-sparse FlashAttention을 제안한다. 이것은 희소성에 비례하는 계수를 이용하여 FlashAttention 보다 더 적은 IO 복잡도를 갖는다.

입력

\bold{Q}, \bold{K}, \bold{V} \in \mathbb{R}^{N\times d}

와 마스크 행렬

\tilde{\bold{M}} \in \{0, 1\}^{N \times N}

이 주어지면, 다음을 계산하기를 원한다.

\begin{aligned} \bold{S} &= \bold{QK}^\top \in \mathbb{R}^{N \times N} \\ \bold{P} &= \text{softmax}(\bold{S} \odot \bold{1}_{\tilde{\bold{M}}}) \in \mathbb{R}^{N \times N} \\ \bold{O} &= \bold{PV} \in \mathbb{R}^{N \times d} \end{aligned}

여기서

\tilde{\bold{M}}_{kl} = 1

이면

(\bold{S} \odot\bold{1}_{\tilde{\bold{M}}})_{kl} = \bold{S}_{kl}

이고

\bold{M}_{kl} = 0

이면

-\infty

이다.

\tilde{\bold{M}}

은 블록 형태를 가져야 한다. 어떤 블록 크기

B_r, B_c

에 대해, 모든

k,l

에 대해

\tilde{\bold{M}}_{kl} = \bold{M}_{ij}

이고 여기서

i = \lfloor k/B_r\rfloor, j = \lfloor l/B_c\rfloor

이고,

\bold{M} \in \{0, 1\}^{N/B_r \times N/B_c}

미리 정의된 block 희소성 마스크

\bold{M} \in \{0, 1\}^{N/B_r \times N/B_c}

가 주어지면 Algorithm 1을 쉽게 수정하여 attention 행렬의 non-zero 블록만 쉽게 계산할 수 있다. 그 알고리즘은 Algorithm 1과 동등하지만 zero 블록을 skip 한다. 부록 B의 Algorithm 5에 알고리즘 설명을 다시한다.

우리는 또한 block-sparse FlashAttention의 IO 복잡도를 분석한다.

Proposition 4.

N

을 시퀀스 길이,

d

를 head 차원,

\bold{M}

을 SRAM의 크기라고 하고

d \le M \le Nd

라 하자. Block-sparse FlashAttention(Algorithm 5)는

\Theta(Nd + N^2d^2M^{-1}s)

HBM 접근을 요구한다. 여기서

s

는 block-sparsity 마스크에서 non-zero 블록의 비율이다.

block-sparsity를 적용하면 희소성에 의해 IO 복잡성에서 더 큰 항에 대해 직접적인 개선이 발생함을 알 수 있다. 긴 시퀀스 길이

N

에 대해

s

는 종종

N^{-1/2}

또는

N^{-1} \log N

으로 설정되어

\Theta(N\sqrt{N})

또는

\Theta(N \log N)

의 IO 복잡도가 된다. downstream 실험에서 임의의 희소성을 근사할 수 있는 것으로 알려진 fixed butterfly sparsity 패턴을 사용한다.

그림 2(오른쪽)에서 우리는 block-sparse FlashAttention의 실행시간이 희소성이 증가함에 비례하여 개선되는 것을 검증한다. LRA 벤치마크에서 block-sparse FlashAttention은 2.8x 속도 개선을 달성하면서 표준 attention과 동등한 성능을 수행한다(섹션 4).

4 Experiments

우리는 Transformer 모델을 학습에 FlashAttention을 사용하는 것의 영향을 평가한다. 우리는 학습 시간과 모델 정확도에 관한 2가지 주장을 검증하고 attention 실행시간과 메모리 벤치마크를 리포트 한다.

•

Training Speed. FlashAttention은 표준 Transformer에 대해 BERT에 대한 MLPerf 1.1 속도 기록을 15% 능가하며, GPT-2을 HuggingFace 대비 최대 3배, Megatron 대비 1.8배 이상 능가한다. FlashAttention은 Long-Range Arean(LRA) 벤치마크를 2.4배 개선한다.

•

Quality. FlashAttention은 Transformer를 더 긴 시퀀스로 확장하여 더 높은 품질을 산출한다. FlashAttention은 GPT-2를 컨텍스트 4K 길이로 학습한다. 이것은 컨텍스트 길이 1K로 사용하여 GPT-2를 학습한 Megatron에 비해 더 빠르고 perplexity도 0.7 더 낮다. 더 긴 시퀀스를 모델링하여 두 가지 긴 문서 분류 작업에 대해 6.4점을 끌어 올렸다. 마지막으로 FlashAttention은 도전적인 Path-X 작업(시퀀스 길이 16K)에서 우연 보다 나은 성능을 달성한 최초의 Transformer이고 block-sprase FlashAttention은 우리가 아는 한 Path-256(시퀀스 길이 64K)에서 우연보다 나은 성능을 달성한 최초의 시퀀스 모델이다.

•

Benchmarking Attention. 우리는 시퀀스 길이에 기반한 FlashAttention과 block-sparse FlashAttention의 실행시간과 메모리 성능을 측정한다. FlashAttention의 메모리 사용량이 시퀀스 길이에 따라 선형적으로 확장되며 일반적인 시퀀스 길이(2K까지)에서 표준 attention보다 3배 더 빠르다는 것을 확인한다. 우리는 block-sparse FlashAttention의 실행 시간이 시퀀스 길이에서 선형적으로 확장되며 기존의 모든 근사 attention baseline 보다 더 빠르다는 것을 확인한다. 

추자적인 실험 상세는 부록 E 참조.

4.1 Faster Models with FlashAttention

BERT.

FlashAttention은 우리가 아는 한 가장 빠른 single-node BERT 학습 속도를 산출한다. 우리는 Wikipedia에서 FlashAttention을 사용하여 BERT-large 모델을 학습한다. 표 1은 MLPerf 1.1의 학습 속도 기록을 세운 Nvidia 구현과 비교한다. 우리 구현이 15%더 빠르다.

GPT-2.

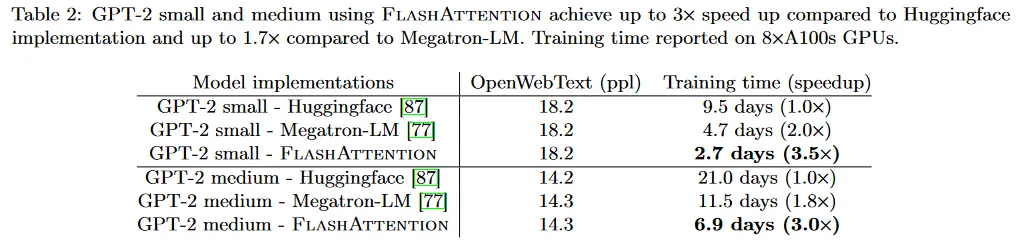
FlashAttention은 대규모 OpenWebtext 데이터셋에서 GPT-2를 학습 시킬 때 널리 사용되는 HuggingFace와 Megatron-LM 보다 더 빠른 학습 속도를 산출한다. 표 2는 HuggingFace와 비교하여 3배 빠르고 Megatron-LM과 비교하여 1.7배 빠른 end-to-end 성능을 보인다. FlashAttention은 모델 정의를 변경하지 않았기 때문에 다른 두 구현과 동일한 perplexity를 달성한다. 부록 E는 학습 전체에 걸친 perplexity 검증을 plot한다. FlashAttention이 baseline만큼 수치적으로 안정적이고 동일한 학습/검증 커브를 생성하는 것을 볼 수 있다.

Long-range Area.

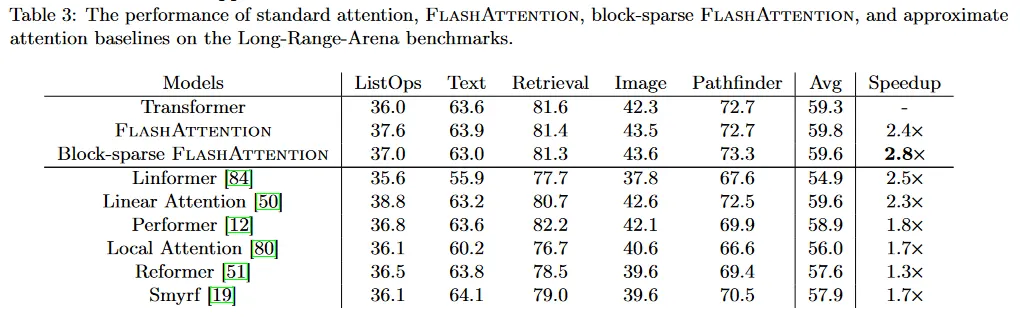
우리는 long-range area(LRA) 벤치마크에 대해 바닐라 Transformer(다른 표준 구현 또는 FlashAttention)와 비교한다. 우리는 모든 모델에 대해 정확도, 처리량, 학습 시간을 측정한다. 각 작업은 1024와 4096 사이에서 다양한 시퀀스 길이 변화를 갖는다. 우리는 Tay et al.와 Xiong et al.에서의 구현과 경험적 설정을 따른다. 표 3은 FlashAttention이 표준 attention과 비교하여 2.4배 빠른 속도를 달성함을 보인다. Block-sparse FlashAttention은 우리가 테스트한 모든 근사 attention 방법 보다 빠르다.

4.2 Better Models with Longer Sequences

Language Modeling with Long Context.

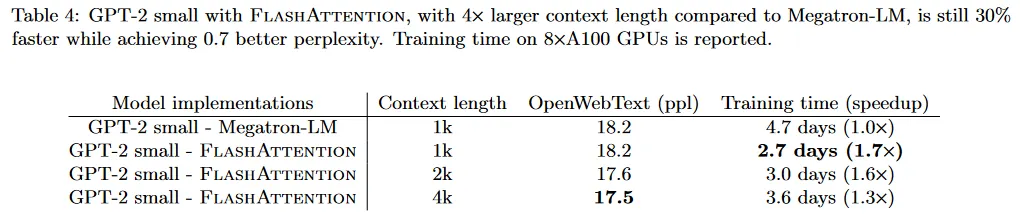
FlashAttention의 실행시간과 메모리 효율성은 GPT-2의 컨텍스트 길이를 4배까지 증가시키지만 Megatron-LM에서 최적화된 구현보다 여전히 실행이 빠르다. 표 4는 FlashAttention과 컨텍스트 길이 4K를 사용하는 GPT-2가 컨텍스트 길이 1K를 사용하는 Megatron의 GPT-2 보다 여전히 30% 더 빠르면서 perplexity가 0.7 더 낮다는 것을 보인다.

Long Document Classification.

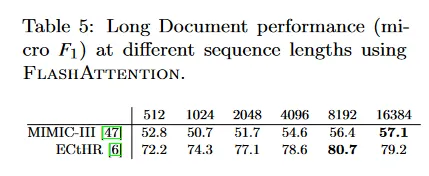
FlashAttention을 사용하여 더 긴 시퀀스로 Transformer를 학습하면 MIMIC-III과 ECtHR 데이터셋에서 성능이 향상된다. MIMIC-III은 중환자실 환자 퇴원 요약이 포함되어 있으며, ECtHR은 유럽 인권 재판소의 법률 사례를 포함한다. 각각은 침해 되었다고 주장되는 인권 협약 조항에 매핑된다. 이 두 데이터셋 모두 매우 긴 텍스트 문서를 포함한다. MIMIC에서 평균 토큰 수는 2,395 토큰이고, 가장 긴 문서는 14,562 토큰을 갖는다. 한편 ECtHR의 평균과 가장 긴 토큰 수는 각각 2,197과 49,392이다. 우리는 pretrained RoBERTa 모델의 시퀀스 길이를 증가시키면서 발생하는 성능 향상을 평가한다.(Beltagy et al.과 같이 positional embedding을 반복한다.)

표 5는 시퀀스 길이 16K가 MIMIC에서 길이 512보다 4.3점 높은 성능을 보이며, 시퀀스 길이 8K가 ECtHR에서 길이 512보다 8.5 점 높은 성능을 보인다. 이러한 차이는 미묘한 분포 이동 때문일 수 있다. MIMIC-III은 특화된 의학 텍스트를 포함하고 따라서 도메인 길이에 따라 분포 이동에 더 취약할 수 있는 반면 ECtHR은 일반적인 언어를 포함한다.

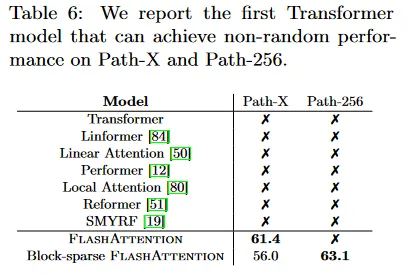
Path-X and Path-256.

Path-X와 Path-256 벤치마크는 긴 컨텍스트를 테스트하기 위해 설계된 long-range arena 벤치마크에서 도전적인 과제이다. 이 작업은 128x128(또는 256x256) 이미지에서 검정과 흰색 두 점이 연결된 경로가 있는지 여부를 판별하는 것이다. 이미지는 한 번에 한 픽셀씩 transformer에 공급된다. 이전 작업에서 모든 transformer 모델은 out of memory 또는 random 성능만을 달성했다. 긴 컨텍스트를 모델링할 수 있는 대안 아키텍쳐에 대한 연구가 있었다. 우리는 Path-X와 Path-256을 해결한 첫 번째 Transformer 모델의 결과를 제시한다(표 6). 우리는 Path-64에 transformer를 pre-train하고 positional embedding을 공간적으로 보간하여 Path-X로 전이했다. FlashAttention은 Path-X에 대해 61.4의 정확도를 달성했고, block-sparse FlashAttention은 Transformer를 시퀀스 길이 64K까지 확장하여 Path-256에 대해 63.1 정확도를 달성했다.

4.3 Benchmarking Attention

우리는 40GB HBM의 A100 GPU 하나에서 dropout과 padding mask를 사용하여 FlashAttention과 block-sparse FlashAttention의 시퀀스 길이를 변화시키고 실행 시간과 메모리 사용량에 대한 측정을 다양한 attention baseline과 비교한다. 우리는 정확한 attention, 근사 attention과 희소 attention에 대한 참조 구현과 비교한다. 본문에서는 baseline의 일부만 리포트하고, 더 많은 baseline과 전체 세부 사항은 부록 E에 포함한다.

Runtime.

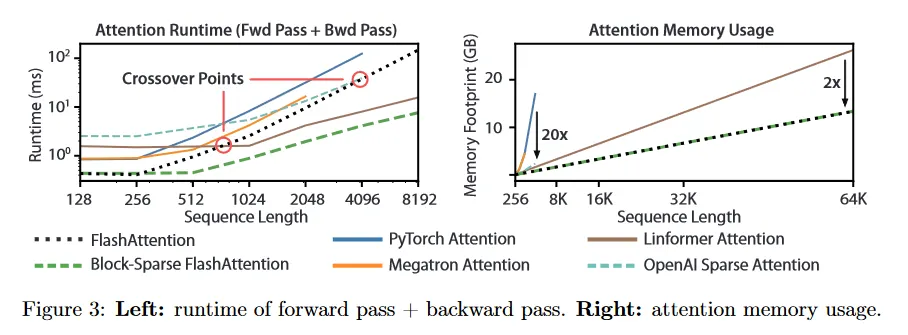
그림 3(왼쪽)은 FlashAttention과 block-sparse FlashAttention의 forward+backward pass의 밀리초 실행시간을 정확한, 근사, 희소 attention의 baseline과 비교한다(정확한 수치는 부록 E). 실행은 시퀀스 길이에 따라 2차적으로 증가하지만, FlashAttention은 정확한 attention baseline보다 매우 빠르며, PyTorch 구현보다 최대 3배까지 빠르다. 많은 근사/희소 attention 메커니즘의 실행시간이 시퀀스 길이에 따라 선형적으로 증가하지만 FlashAttention은 더 적은 메모리 접근 때문에 짧은 시퀀스 길이에서 여전히 근사와 희소 attention 보다 빠르다. 근사 attention 실행은 시퀀스 길이 512와 1024 사이에서 FlashAttention과 교차하기 시작한다. 반면에 block-sparse FlashAttention은 우리가 아는 한 모든 정확한, 희소 그리고 근사 attention보다 모든 시퀀스 길이에서 빠르다.

Memory Footprint.

그림 3(오른쪽)은 FlashAttention과 block-sparse FlashAttention의 메모리 사용량을 다양한 정확한, 근사, 희소 attention baseline과 비교한다. FlashAttention과 block-sparse FlashAttention은 동일한 메모리 사용량을 가지며 이것은 시퀀스 길이에 따라 선형적으로 증가한다. FlashAttention은 정확한 attention baseline보다 최대 20배 더 메모리 효율적이고 근사 attention baseline보다 더 메모리 효율적이다. Linformer를 제외한 모든 다른 알고리즘은 64K 이전에 A100 GPU에서 out of memory를 겪지만, FlashAttention은 Linformer 보다도 2배 더 효율적이다.

5 Limitations and Future Directions

우리 접근의 한계와 미래 방향에 대해 논의한다. 관련된 작업은 부록 A에 제공된다.

Compiling to CUDA.

현재 우리의 접근은 새로운 attention 구현마다 새로운 CUDA 커널을 작성해야 한다. 이를 위해서는 PyTorch 보다 상당히 낮은 수준의 언어로 attention 알고리즘을 작성해야 하며, 상당한 엔지니어링 노력이 필요하다. 또한 구현이 GPU 아키텍쳐 간에 이전되지 않을 수 있다. 이런 한계점은 고수준 언어(예: PyTorch)로 attention 알고리즘을 작성하고, 이를 CUDA의 IO-aware 구현으로 컴파일 할 수 있는 방법이 필요함을 시사한다. 이는 이미지 처리 분야의 Halide와 같은 노력과 유사하다.

IO-Aware Deep Learning.

우리는 IO-aware 접근이 attention 너머로 확장될 수 있으리라 믿는다. Attention은 Transformer에서 가장 메모리 집약적인 계산이지만, 심층 네트워크에서 모든 레이어가 GPU HBM을 터치한다. 우리는 우리의 작업이 추가적인 모듈의 IO-aware 구현에 영감을 일으키길 희망한다. 부록 D에서 이러한 잠재적인 확장을 논의한다.

Multi-GPU IO-Aware Methods.

우리의 IO-aware attention 구현은 단일 GPU에서 attention을 계산하는데 있어 상수 수준에서 최적이다. 그러나 attention 계산은 여러 GPU에 걸쳐 병렬화 할 수 있다. 여러 GPU를 사용하면 IO 분석에 추가적인 layer가 추가된다. 즉 GPU 사이의 데이터 전송을 고려해야 한다. 우리는 우리의 작업이 이 방향에서 미래 작업에 영감을 주기를 희망한다.