1 Introduction
이전에 우리는 일반적인 카메라 calibration 절차 또는 single view metrology를 사용하여 하나 이상의 view에서 카메라의 intrinsic과 extrinsic 파라미터를 계산하는 방법을 보았다. 이 과정을 통해 하나의 이미지에서 3d 세계에 관한 속성을 유도할 수 있었다. 그러나 일반적으로 단일 이미지만으로 3d 세계의 전체 구조를 복구하는 것은 불가능하다. 이것을 3d를 2d로 매핑하는 것의 내재적 모호함 때문이다. 일부 정보는 단순히 손실된다.
예컨대 그림 1에서 처음에 그 사람이 Pisa의 Learning Tower를 들고 있는 것으로 오해할 수 있다. 하지만 주의 깊게 관찰하면 이것이 사실이 아니라 단지 서로다른 depth를 이미지 평면에 투영하여 생긴 착시일 뿐임을 알 수 있다. 그러나 이 장면을 완전히 다른 각도에서 볼 수 있다면 이 착시는 즉각 사라지고 즉시 올바른 장면 레이아웃을 계산할 수 있다.
이 강의 노드의 초점은 여러 카메라가 존재할 때 geometry의 지식이 매우 도움이 될 수 있음을 보이는 것이다. 구체적으로 우리는 먼저 2가지 viewpoint에 관여하는 geometry를 정의한 다음, 이 geometry가 우리를 둘러싼 세계를 더 잘 이해하는데 어떻게 도움이 될 수 있는지를 설명한다.
2 Epipolar Geometry
여러 view geometry에서 종종 여러 카메라, 3d 점과 각 카메라의 이미지 평면에서 그 점의 투영 사이에 흥미로운 관계가 존재한다. 카메라, 3d 점과 해당하는 관측치를 연결하는 geometry를 stereo 쌍의 epipolar geometry라고 부른다.
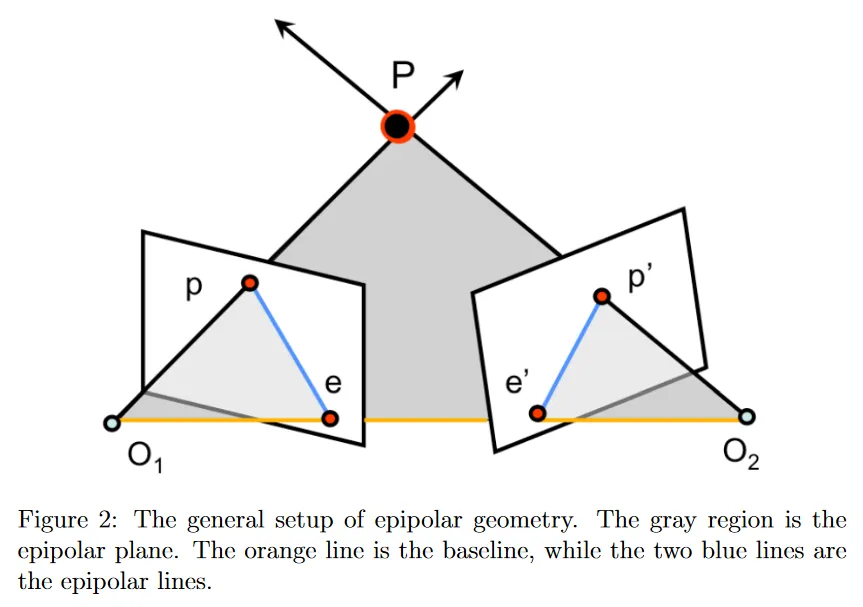
그림 2에 나온대로 표준 epipolar geometry 설정은 동일한 3d 점 를 관찰하는 2대의 카메라가 포함된다. 각 이미지 평면에서의 의 투영은 각각 와 에 위치한다. 카메라 중심은 과 에 있으며 이들 사이의 직선을 baseline이라 부른다. 두 카메라 중심과 에 의해 정의된 평면을 epipolar plane이라 부른다. baseline이 두 이미지 평면과 교차하는 지점을 epipole 와 라 부른다. 마지막으로 epipolar 평면과 두 이미지 평면의 교차로 정의되는 선을 epipolar line이라 부른다. epipolar line은 이미지 평면에서 각각의 epipole에서 baseline을 교차하는 속성을 갖는다.
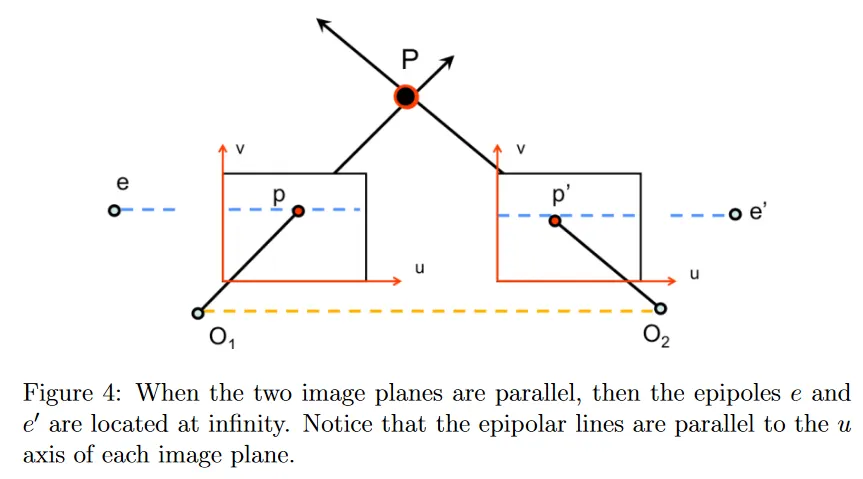
epipolar geometry의 흥미로운 경우는 그림 4에 보여진다. 이것은 이미지 평면이 서로 평행할 때 발생한다. 이미지 평면이 서로 평행하면 중심 를 결합하는 baseline이 이미지 평면과 평행하기 때문에 epipole 와 는 무한대에 위치한다. 이 경우의 또 다른 중요한 byproduct(부산물)은 epipolar line이 각 이미지 평면의 축과 평행하다는 것이다. 이 경우는 특히 유용하며 이미지 rectification에 대한 후속 섹션에서 더 상세히 커버된다.
그러나 현실 상황에서 3d 위치 의 정확한 위치는 주어지지 않고, 한 이미지 평면에서 그것의 투영만 로 결정할 수 있다. 또한 카메라 location, orientation, camera matrix를 알 수 있다. 이 지식을 사용하여 무엇을 할 수 있는가? 카메라 위치 와 이미지 점 를 알면 epipolar plane을 정의할 수 있다. 그러면 이 epipolar plane을 사용하여 epipolar line을 결정할 수 있다. 정의에 따라 의 두 번째 이미지에 대한 투영 은 반드시 두 번째 이미지의 epipolar line 상에 위치해야 한다. 따라서 epipolar geometry의 기본 이해를 통해 장면의 3d 구조를 모르더라도 이미지 쌍 사이의 강력한 제약조건을 만들 수 있다.
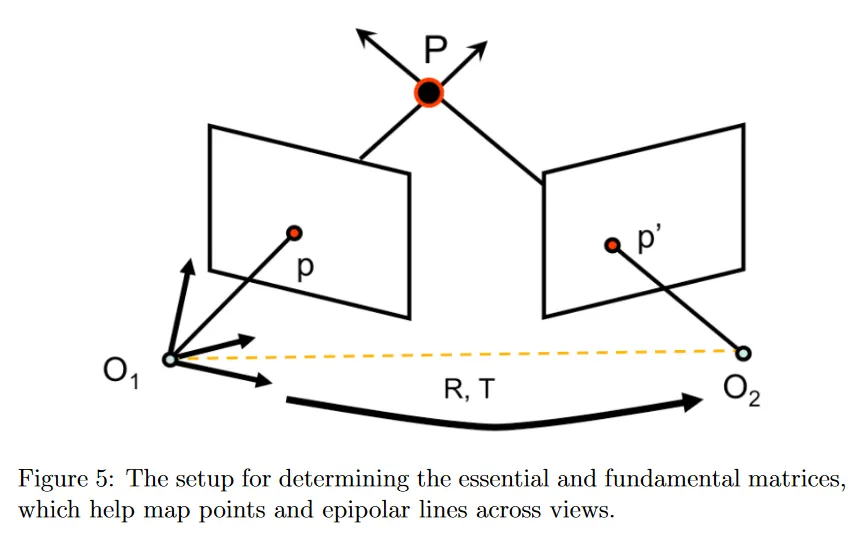
이제 점과 epipolar line을 view에 걸쳐 seamless 매핑하는 방법을 개발해 보겠다. 원래의 epipolar geometry framework(그림 5)에서 주어진 설명을 취하면, 추가로 과 을 각각 3d 점을 해당 2d 이미지 평면 위치로 매핑하는 카메라 projection matrix로 정의할 수 있다.
world reference system이 첫 번째 카메라와 연관되어 있고, 두 번째 카메라는 먼저 rotation 한 다음 translation 만큼 offset되어 있다고 가정하자. 이것은 카메라 projection 행렬을 다음과 같이 지정한다.
3 The Essential Matrix
가장 단순한 경우에서 인 canonical camera를 갖는다고 가정한다. 이것은 방정식 1을 다음으로 축소한다.
추가로 이것은 첫 번째 카메라의 reference system에서 의 위치가 라는 것을 의미한다. 벡터 와 가 epipolar plane에 놓이기 때문에 의 cross product를 취하면, epipolar plane에 normal인 vector를 얻을 수 있다. 이것은 또한 epipolar plane에 놓인 가 에 대해 normal임을 의미하므로 그들의 dot product가 0이라는 제약조건을 얻는다.
선형대수에서 cross product에 대한 다양하고 간결한 표현을 유도할 수 있다. 우리는 임의의 두 벡터 와 사이의 cross product를 행렬-벡터 곱으로 표현할 수 있다.
이 표현식을 방정식 3과 결합하여 cross product 항을 행렬 곱으로 변환할 수 있다.
행렬 은 Essential Matrix라고 하며, epipolar 제약조건에 대한 간결한 표현식을 생성한다.
Essential 행렬은 5개 자유도를 갖는 행렬이다. 이것은 rank 2이고 singular이다.
Essential 행렬은 와 와 연관된 epipolar line을 계산하는데 유용하다. 예컨대 는 카메라 2의 이미지 평면에서 epipolar line을 제공한다. 유사하게 는 카메라 1의 이미지 평면에서 epipolar line을 제공한다.
Essential matrix의 다른 흥미로운 속성은 epipole과 dot product하면 0이 된다는 것이다. . 카메라 1의 이미지에서 임의의 점 ( 제외)에 대해, 카메라 2의 이미지에서 해당하는 epipolar line 가 epipole 를 포함한다. 따라서 는 모든 에 대해 를 만족하므로 이다. 유사하게 이다.
4 The Fundamental Matrix
canonical 카메라를 가졌을 때 와 사이의 관계를 유도했지만, 카메라가 canonical이 아닐 때 더 일반적인 표현식을 찾을 수 있어야 한다. projection matrix가 다음과 같이 주어짐을 떠올려라.
우선 카메라가 canonical일 때 카메라 이미지에 대한 의 투영이도록 와 를 정의한다. canonical 경우에서는 다음을 떠올려라
와 의 값을 교체하여 다음을 얻는다.
행렬 은 Fundamental Matrix라고 한다. 이것은 이전 섹션의 Essential Matrix와 유사하게 작동하지만 카메라 행렬 와 카메라 사이의 상대적 translation 와 rotation 에 관한 정보도 인코딩한다. 따라서 카메라 행렬 와 변환 가 알려지지 않은 경우에도 와 와 관련된 epipolar line을 계산하는데 유용하다. Essential matrix와 유사하게 Fundamental matrix와 해당하는 점만으로 epipolar line 와 를 계산할 수 있다. Fundamental matrix와 Essential matrix 사이의 주요한 차이 중 하나는 Fundamental matrix가 7개 자유도를 포함하는데 반해 Essential matrix는 5개의 자유도를 포함한다는 것이다.
그러나 Fundamental matrix가 어떻게 유용한가? Essential matrix와 유사하게 Fundamental matrix를 알면 이미지에서 점만 알아도 다른 이미지에서 해당하는 점에 대한 쉬운 제약조건(epipolar line)을 얻을 수 있다. 따라서 3d 공간에서 의 실제 위치나 카메라의 extrinsic 또는 intrinsic 특성을 모르더라도 임의의 와 사이의 관계를 설정할 수 있다.
4.1 The Eight-Point Algorithm
그렇지만 Fundamental matrix이 카메라 파라미터의 행렬 곱에 의해 정의된다는 가정은 다소 무리가 있어 보인다. 하지만 동일한 장면의 두 이미지가 주어지고 카메라의 extrinsic 또는 intrinsic 파라미터를 모르더라도 Fundamental matrix를 추정하는 것이 가능하다. 이를 위해 논의하는 방법을 Eight-Point Algorithm이라 부른다. 이것은 1981년 Longuet-Higgins에 의해 제안되었고 1995년 Hartley에 의해 확장되었다. 제목에서 알 수 있듯이 Eight-Point Algorithm은 두 이미지 사이에 최소 8쌍의 대응점 집합이 가능하다고 가정한다.
각 대응점 과 은 epipolar 제약 을 제공한다. 이 제약조건을 다음처럼 재형식화할 수 있다.
이 제약이 스칼라 방정식이기 때문에 1개의 자유도만 제약한다. Fundamental matrix은 scale까지만 알 수 있기 때문에 Fundamental matrix를 결정하기 위해 이러한 제약조건 8개가 필요하다.
이것을 다음처럼 간략히 작성할 수 있다.
여기서 는 개 대응점에서 유도된 행렬이고 는 우리가 원하는 Fundamental 행렬의 값이다.
실제로는 noisy 측정의 효과를 줄이기 위해 8개 이상의 대응점과 더 큰 행렬을 사용하는 것이 좋다. 이 homogeneous 방정식 시스템의 해는 를 rank-deficient(부족한)이므로 Singular Value Decomposition(SVD)를 통해 least-squares의 의미에서 찾을 수 있다. SVD를 통해 Fundamental 행렬 추정치 를 얻게 되는데 이것은 full rank일 수 있다. 그러나 실제 Fundamental 행렬이 rank 2라는 사실을 알고 있다. 따라서 best rank-2 근사치를 찾아야 한다. 이를 위해 다음의 최적화 문제를 해결해야 한다.
이 문제는 다시 SVD로 해결된다. 여기서 . 그러면 best rank-2 근사는 다음과 같이 찾을 수 있다.
4.2 The Normalized Eight-Point Algorithm
실제로 Eight-Point Algorithm에 대한 표준 least-squares 접근은 정확하지 않다. 종종 점 와 그것에 해당하는 epipolar line 사이의 거리는 매우 큰데, 일반적으로 10 픽셀 이상이다. 이 에러를 줄이기 위해 Eight-Point Algorithm의 수정된 버전인 Normalized Eight-Point Algorithm을 고려할 수 있다.
표준 Eight-Point Algorithm stem의 주요 문제는 가 SVD에 대해 ill-conditioned 라는 사실에 있다. SVD가 제대로 작동하려면 의 singular value 중 하나는 0 (또는 가까운)이어야 하고 다른 singular 값은 nonzero이어야 한다.
그러나 대응점 은 현대 카메라의 픽셀 범위 때문에(예: ) 첫 번째와 두 번째 좌표에서 종종 매우 큰 값을 가진다. 를 구성하기 위해 사용된 이미지 점들이 이미지의 상대적으로 작은 영역에 존재하면, 일반적으로 와 에 대한 벡터가 매우 유사할 것이다. 결과적으로 구성된 행렬은 하나의 매우 큰 singular 값과 나머지는 상대적으로 작은 값을 갖게 된다.
이 문제를 해결하기 위해 를 구성하기 전에 이미지의 점들을 normalize 해야 한다. 이것은 이미지 좌표에 translation과 scaling을 모두 적용하여 를 pre-condition(전처리) 하는 것을 의미한다.
이렇게 하면 두 가지 요구사항이 충족된다. 첫째, 새로운 좌표 시스템의 원점은 이미지 점들의 centroid에 위치 해야한다(translation). 둘째, 변환된 이미지 점들의 원점에서의 평균 제곱 거리는 2 pixel 이어야 한다(scaling). 이 절차를 centroid로 translate하고 scaling factor로 scale하는 행렬 를 간결하게 표현할 수 있다.
각 이미지 마다.
그 다음 좌표를 normalize 한다.
새로운 normalized 좌표를 사용하여 regular least-squares Eight Point Algorithm을 사용하여 새로운 를 계산할 수 있다. 그러나 행렬 는 normalized 좌표에 대한 fundamental matrix이다. regular 좌표 공간에서 사용할 수 있도록 de-normalize 해야 한다.
궁극적으로 이 새로운 Fundamental matrix 는 현실 세계 응용에서 좋은 결과를 제공한다.
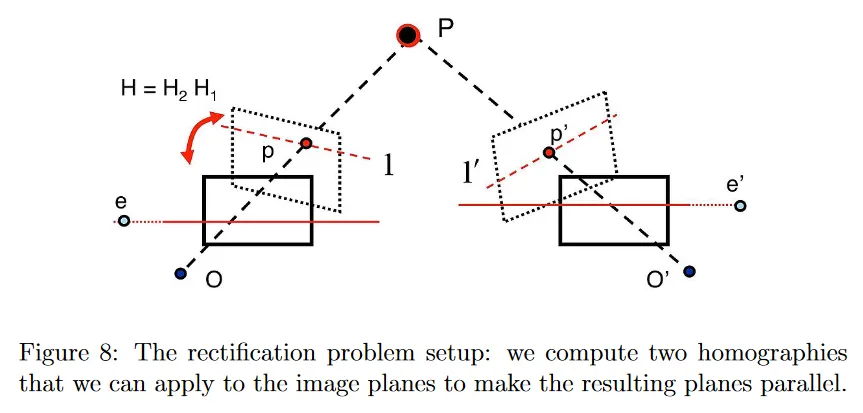
5 Image Rectification
두 이미지가 서로 평행할 때 epipolar geometry에 흥미로운 경우가 나타난다는 사실을 떠올려라. 우선 평행 이미지 평면의 경우에서 Essential matrix 를 계산한다. 두 카메라가 동일한 를 갖고 카메라 사이에 상대적 회전이 없다()고 가정할 수 있다. 이 경우에 축을 따라 translation만 존재한다고 가정하면 이 된다. 그러면 다음과 같이 된다.
가 알려지면, 이미지 평면의 점과 연관된 epipolar line의 방향을 찾을 수 있다. 점 와 연관된 epipolar line 의 방향을 계산한다.
유사한 방법으로 계산될 수 있는 의 방향과 유사하게 의 방향이 horizontal 임을 알 수 있다.
epipolar 제약 조건 을 사용하면 가 되어 와 가 동일한 -좌표를 공유한다는 사실을 알 수 있다. 결과적으로 대응점 사이에 매우 간단한 관계가 존재한다. 그러므로 주어진 두 이미지를 평행으로 만드는 과정인 rectification은 이미지에서 대응점 사이의 관계를 discerning(식별력 있는) 때 유용하다.
이미지의 쌍을 Rectifying 하는데 두 카메라 행렬 이나 그들 사이의 상대적 변환 에 대한 지식이 필요하지 않다. 대신 Normalized Eight Point Algorithm에 의해 추정된 Fundamental matrix를 사용할 수 있다. Fundamental matrix를 얻으면 각 대응점 와 에 대한 epipolar line 와 를 계산할 수 있다.
그러면 epipolar line의 집합에서 각 이미지의 epipole 와 를 추정할 수 있다. 이것은 epipole이 모든 epipolar line의 교차에 놓인다는 것을 알기 때문이다. 실제로는 noisy 측정 때문에 모든 epipolar line이 단일 점에서 교차하지 않는다. 따라서 epipole 계산은 모든 epipolar line에 점을 맞추는 least squared error를 최소화하여 찾을 수 있다. 각 epipolar line은 벡터 로 표현될 수 있으며, 직선 위의 모든 점(homogeneous 좌표로 표현됨)이 집합 에 존재한다. 각 epipolar line을 로 정의하면 선형 시스템의 방정식을 세우고 SVD를 사용하여 epipole 를 찾을 수 있다.
epipole 와 를 찾은 후에 아마도 그것들이 horizontal axis를 따라 무한대에 있는 점이 아니라는 것을 알게 될 것이다. 만약 그랬다면 정의에 의해 이미지가 이미 평행이어야 한다. 따라서 이미지를 평행하게 만드는 방법에 대한 통찰을 얻을 수 있다. 즉, epipole 를 horizontal axis를 따라 무한대로 매핑하는 homography를 찾을 수 있는가?
구체적으로 이것은 epipole을 무한대로 매핑하기 위해 이미지에 적용할 수 있는 homographies의 쌍 를 찾고 싶다는 뜻이다. 먼저 두 번째 epipole 를 horizontal 축 상의 무한대 점으로 매핑하는 homography 를 찾는 것에서 시작하자. 이러한 homography에 가능한 선택이 많기 때문에 합리적인 것을 선택 해야 한다. 실제로 좋은 결과를 이끄는 한 가지 조건은 homography가 이미지의 중심에 가까운 점에 대해 translation과 rotation을 적용하는 변환처럼 작용하도록 하는 것이다.
이런 변환을 달성하는 첫 번째 단계는 두 번째 이미지를 homogeneous 좌표에서 중심이 이 되도록 translate 하는 것이다. 이를 위해 다음과 같은 translation matrix를 적용할 수 있다.
translation을 적용한 후에 epipole을 horizontal axis 상에 어떤 점 에서 배치하도록 rotation을 적용한다. 평행이동 된 epipole 가 homogeneous 좌표 에 위치한다면 적용되는 rotation은 다음과 같다.
여기서 이면 이고 그렇지 않으면 이다. 이 rotation을 적용한 후에 의 임의의 점을 horizontal axis 상의 무한대 점 으로 가져오려면 다음과 같은 변환만 적용하면 된다.
이 변환을 적용한 후에 마침내 무한대에 있는 epipole을 갖게 되므로 regular 이미지 공간으로 다시 translate 할 수 있다. 따라서 두 번째 이미지를 rectify하기 위해 적용하는 homography 는 다음과 같다.
이제 유효한 를 발견했으므로 첫 번째 이미지에 대해 일치하는 homography 을 찾아야 한다. 이미지의 대응점 사이의 제곱 거리의 합을 최소화하는 변환 을 찾아 이를 수행한다.
유도가 이 수업의 범위를 벗어나지만 일치하는 이 다음 형식을 갖는다는 것을 증명할 수 있다.
여기서 이고
여기서 은 나중에 계산될 특정한 벡터 의 성분을 구성한다.
우선 에 대해 알아야 한다. 임의의 skew-symmetric matrix 의 흥미로운 속성은 (scale까지)라는 것이다. 임의의 cross product matrix 가 skew-symmetric이고 Fundamental matrix 는 scale까지만 알 수 있으므로
우변을 그룹화하여 다음을 찾을 수 있다.
의 열에 의 임의의 스칼라 곱을 추가해도 은 여전히 scale까지 성립한다. 그러므로 을 정의하는 더 일반적인 경우는 다음과 같다.
어떤 벡터 에 대해. 실제로 로 설정하여 을 매우 잘 정의할 수 있다.
마지막으로 에 대해 구하기 위해 의 값을 계산해야 한다. 방정식 24에서 제시된 문제를 최소화하는 를 찾기를 원한다. 이미 와 의 값을 알고 있으므로 와 로 치환하면 최소화 문제는 다음이 된다.
특히 과 라 하면 최소화 문제는 다음과 같이 바꿀 수 있다.
이 상수 값이므로 최소화 문제는 추가로 다음으로 축소된다.
궁극적으로 이것은 에 대한 least-square 문제 를 해결하는 것으로 분해될 수 있다.
를 계산한 후에 를 계산하고 마지막으로 을 구할 수 있다. 따라서 몇 개의 대응점이 주어지면 이미지 쌍을 rectify 하기 위한 homographies 를 생성할 수 있다.