•
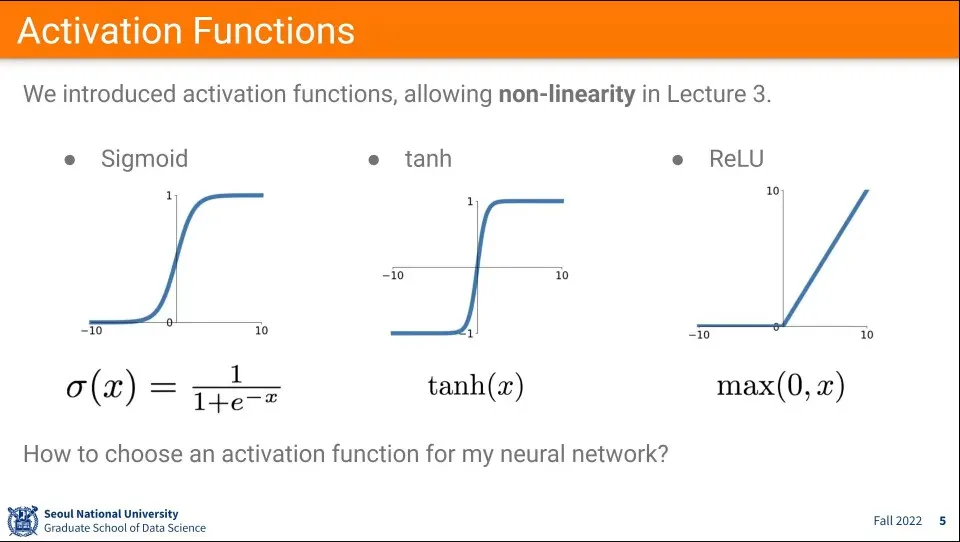
많이 쓰이는 활성화 함수 종류. Sigmoid, tanh, ReLU가 많이 쓰임
•
시그모이드 함수는 input에 대해 e를 이용해서 0-1 사이의 값을 만들어 줌.
◦
이는 확률처럼 보이기 때문에 초기에는 많이 사용했음
•
그러나 시그모이드는 몇 가지 문제가 있음
◦
Gradient를 죽임
◦
값이 양수만 나옴
◦
exponential 함수를 써서 연산이 많이 걸림
•
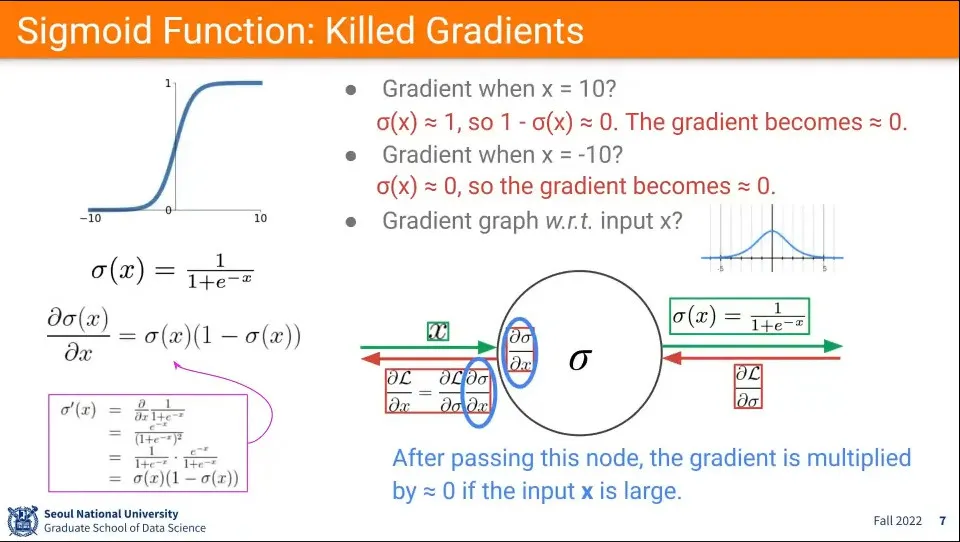
시그모이드 함수에서 input이 5이상의 큰 값이 들어오면 gradient가 0이 되게 됨.
◦
(이미지 중간의 분포도 참고, -5 ~ 5 사이의 분포는 적절한 값을 갖지만 그 범위를 벗어나게 되면 0에 가까운 값이 나옴)
◦
엄밀히 말해 0에 가까운 값이 되지만 layer가 겹겹이 쌓여 있기 때문에 layer를 지나가면서 점점 0으로 수렴하게 됨.
◦
때문에 layer를 점점 지나면서 학습이 이루어지지 않음
•
sigmoid가 0-1 사이의 양수만 나오기 때문에 학습이 항상 양수 방향으로만 진행이 됨
◦
오른쪽 아래 그래프와 같이 최적점이 우하향하는 경우 (파란 화살표) 학습은 우하향하는 방향으로 못가고 (+, +), (-, -)를 반복해서 학습이 됨 (빨간 화살표)
◦
비효율적인 상황 발생
•
비효율적인 문제이므로 앞의 gradient를 죽이는 것보다는 덜 치명적인 문제
•
시그모이드의 문제를 해결하고자 했던게 탄젠트 하이퍼볼릭 함수
•
음의 값이 나오기 때문에 zero-centered 문제는 해결이 되었지만, 근본적으로 탄젠트 하이퍼볼릭은 시그모이드 함수를 2배하고 -1을 준 형태이기 때문에 killing gradients 문제는 해결을 못 함
◦
input이 큰 값이 들어오면 0에 수렴
•
killing gradient 문제를 해결하기 위해 사용하는 것이 ReLU 함수. 어떠한 큰 수가 들어와도 반영이 된다.
◦
더불어 미분을 하지 않기 때문에 연산이 빠르고 그래서 빠르게 최적에 수렴할 수 있음
•
그러나 음수일 경우 0으로 처리하기 때문에 zero-centered 문제가 다시 발생
◦
더불어 0에서 미분이 안 된다는 문제가 존재
◦
또한 input이 음수인 경우 0으로 초기화되어서 학습이 발생하지 않는 Dead ReLU Problem이 발생.
▪
이를 해결하기 위해 초기 값이 음수일 경우 아주 작은 양수 (0.01 정도)의 값을 넣어서 처리한다.
•
ReLU의 문제를 개선해서 음수일 때 아주 작은 값을 사용하는 Leaky ReLU 방법이 나옴
◦
ReLU의 여러 문제를 해결했지만, 음수일 때 기울기를 얼마를 줘야 적당한지는 학습 결과를 보고 결정해 줘야 함
•
Leaky ReLU를 다시 개선한 ELU가 등장
◦
ReLU의 장점을 모두 받아가면서, 0에서도 미분이 가능하고, 음수일 때도 값이 나오기 때문에 학습이 가능함
•
작은 단점은 음수일 경우 exponential 계산 비용이 발생한다는 것
•
Neural Network를 설계할 때 일단 처음에는 ReLU를 써라. learning rate를 잘 조절하면서
•
그 후 결과를 보면서 Leaky ReLU나 ELU를 시도해 봐라
•
sigmoid나 tanh는 중간 단계에서는 쓰지 말고 가장 마지막에 확률 해석을 할 때만 사용한다.
•
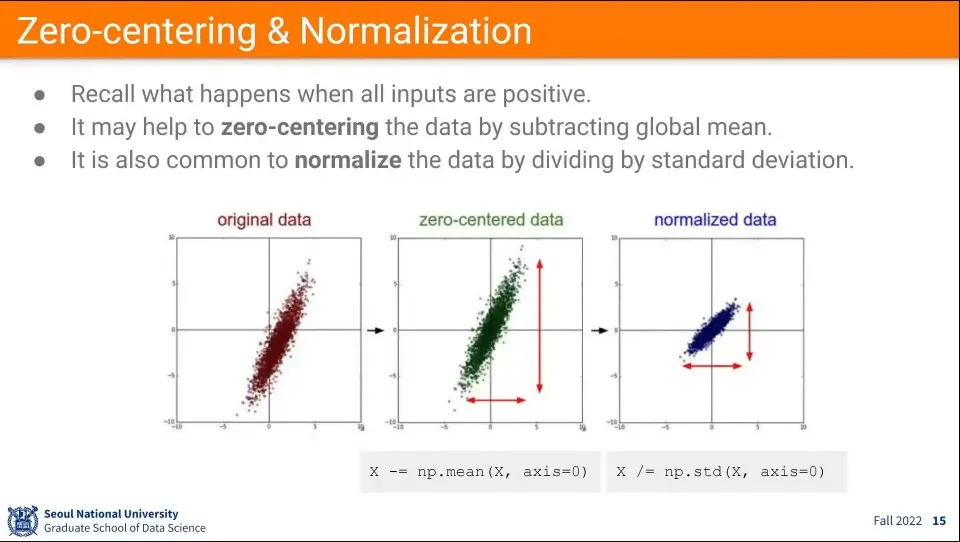
데이터 전처리 단계에서 zero-centering과 normalization을 해준다.
◦
수식은 이미지 참조
•
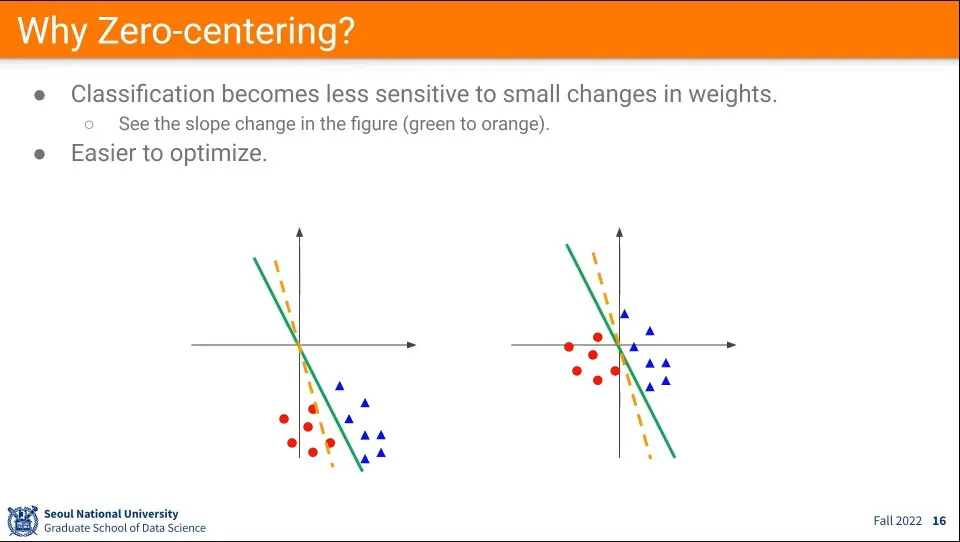
zero centering을 하지 않으면 데이터 분포가 멀리 있기 때문에 값이 조금만 수정되어도 기울기가 크게 바뀜.
◦
데이터가 zero centering 되어 있으면 그게 덜하기 때문에 최적화가 더 쉽다.
•
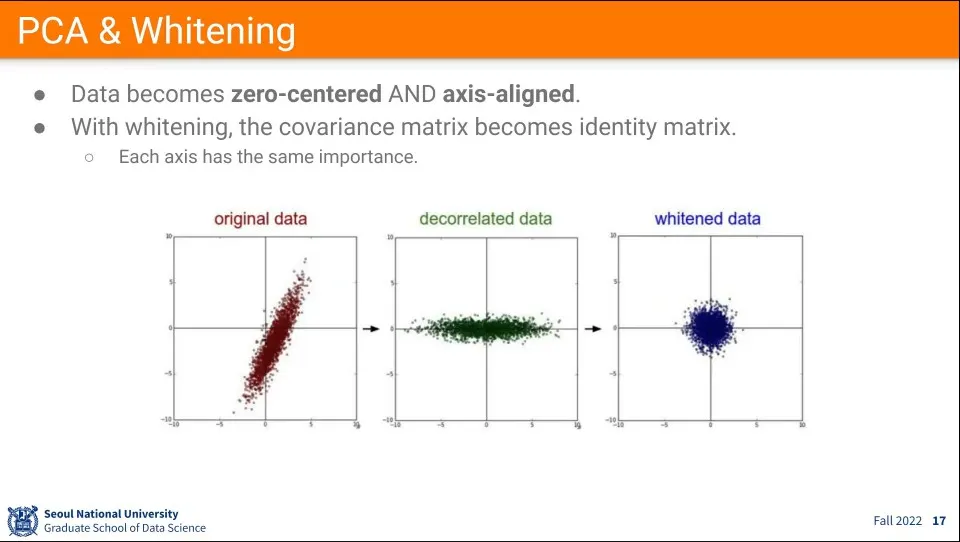
데이터 전처리를 위해 PCA와 Whitening을 할 수 있다.
◦
PCA는 zero-centering과 axis-aligned까지 하는 방법
▪
axis-aligned을 위해 original 데이터의 분산를 계산해서 가장 분산이 많은 축을 x축이 놓고, 2번째로 많은 분포가 첫 번째 분산에 직교하도록 y 축으로 변환해 준다.
▪
PCA 수식은 별도로 찾아볼 것
◦
whitening은 그렇게 정렬된 데이터를 normalize해주는 것
•
데이터를 어떻게 다뤄야할지 모를 때는 일단 이렇게 정렬하고 정규화해주는게 좋다.
•
가지고 있는 이미지에 다양한 변화를 주어서 데이터셋을 풍부하게 만들어주는 것
◦
사람이 인식하기에는 동일하지만, 픽셀 레벨에서는 차이가 발생하는 이미지나 혹은 같은 의미를 갖는 다른 단어로 된 문장을 추가해 주는 것이 이러한 것
◦
사람이 보기에 동일하지만 다른 데이터를 넣어주는게 핵심
◦
이러한 데이터를 모두 학습 데이터를 넣어서 학습할 때 핵심 feature를 올바르게 추출할 수 있게 한다.
•
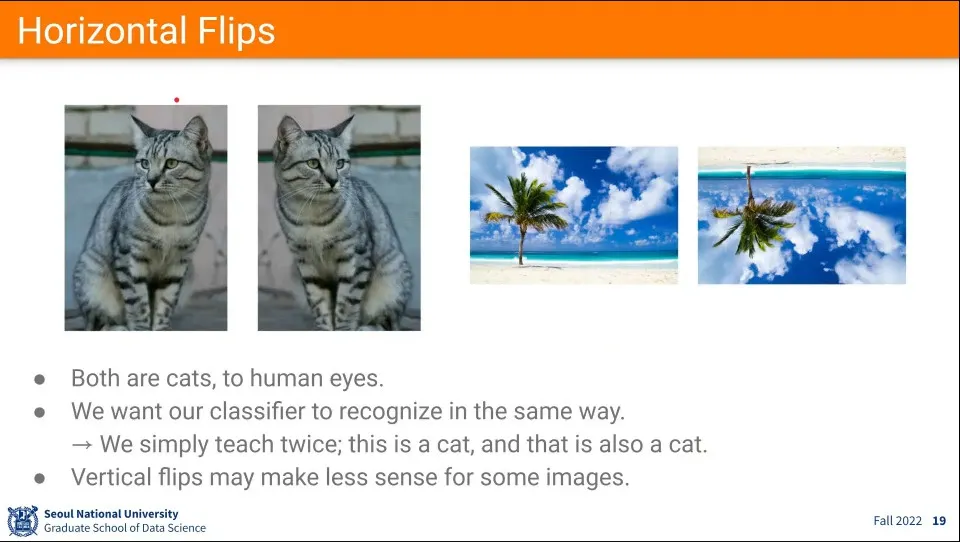
가장 쉬운거는 flip
◦
horizontal flip은 완전히 동일하지만, vertical flip은 중력의 영향 때문에 자연스럽지 않다.
•
데이터의 특정 영역을 crop 하는 것.
◦
이미지나 오디오, 텍스트 데이터에도 사용할 수 있음.
◦
혹은 평행이동도 해줄 수 있다.
•
scaling도 data augmentation 기법 중 하나
•
예시
◦
학습할 때
1.
일단 256-480 사이의 값을 랜덤으로 뽑아서 L로 둔다.
2.
주어진 이미지의 짧은쪽이 L이 되도록 scaling 한다.
3.
그 후에 그 안에서 224x224를 뽑는다.
◦
테스트할 때
1.
5개의 scale로 조절하고
2.
224x224를 10개를 뽑고
3.
그 결과를 보고 평균이나 max를 구해서 고양이인지 아닌지 판단한다.
•
이미지를 224x224를 쓰는 이유는 ImageNet 데이터가 그렇게 맞춰져 있어서 AlexNet을 포함하여 초창기 모델들이 이 사이즈에 맞춰져 학습 되어있기 때문에 관례적으로 사용한다.
•
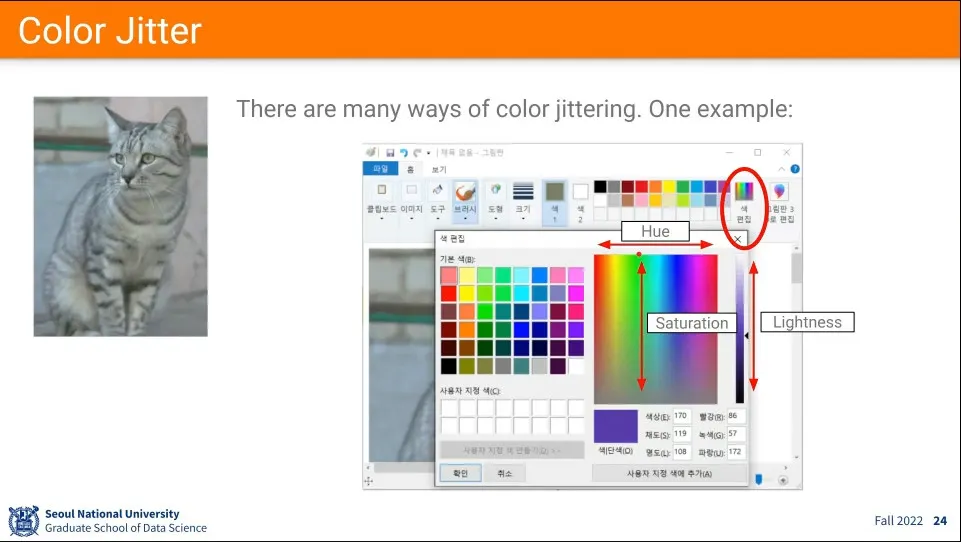
이미지의 light를 바꾸고 싶은 경우 방법
•
HSV를 이용한다.
•
RGB → HSV, HSV → RGB 변환 공식
•
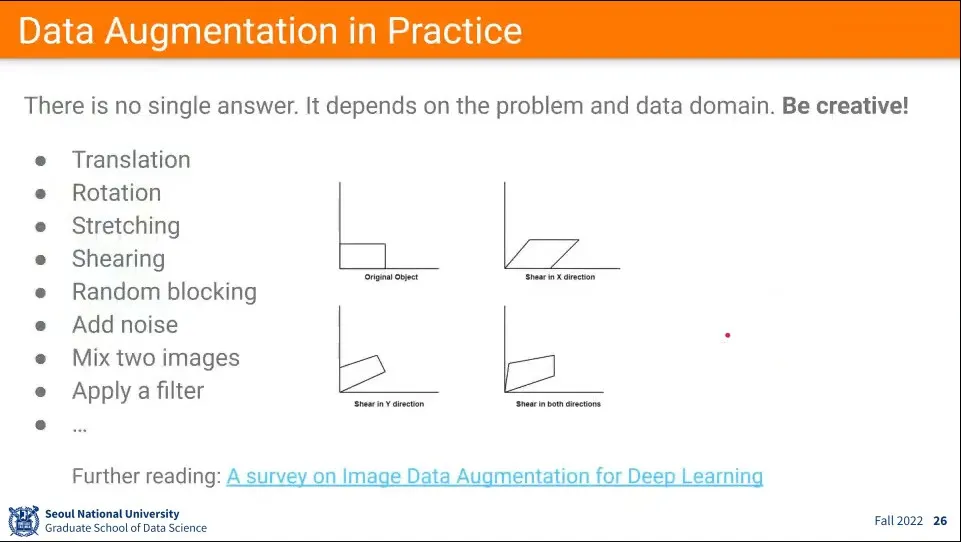
그 외의 Data Augmentation을 할 수 있는 방법 예
◦
이렇게 다양한 방법으로 Data Augmentation을 사용해주면 같은 모델 구조를 쓰면서도 성능을 높일 수 있다고 함.
•
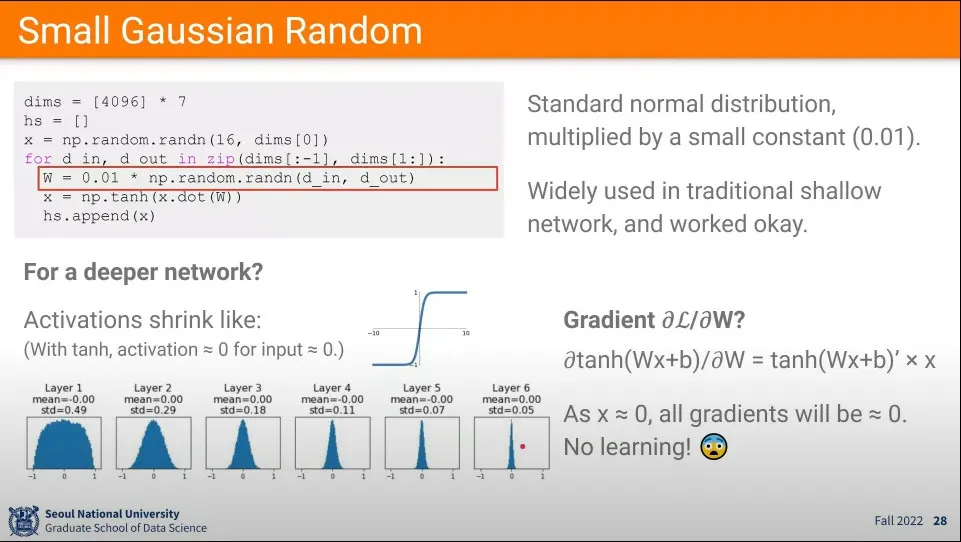
가중치를 초기화할 때 너무 작은 값 이용한 경우
◦
탄젠트 하이퍼볼릭 함수를 사용한다면 layer를 지날 수록 점점 0에 수렴하는 현상이 발생한다.
◦
이유는 tanh를 로 편미분하면 의 모양이 되는데, 가 에 가까워지면 결과가 에 수렴하게 된다.
◦
다시 말해 작은 input이 들어가게 되면 다 이 된다.
•
가중치를 초기화할 때 너무 큰 값을 이용한 경우
◦
이 경우에는 layer를 지날수록 지점에 수렴하는 현상이 발생한다.
◦
이유는 마찬가지로 tanh를 로 편미분하면 의 모양이 되는데, tanh에서 가 양의 방향으로 크면 , 음의 방향으로 크면 에 수렴하게 되고, 이 경우 의 앞부분을 으로 만들기 때문에 결과가 0에 수렴하게 된다.
◦
다시 말해 너무 큰 input이 들어가게 되면 에 수렴하는 모양이 나오게 된다.
•
고로 가중치 초기화를 아무렇게나 하면 안 된다.
•
이를 해결하기 위한 대안으로 위와 같은 초기화 수식이 제안된다. - Xavier Initialization
◦
random 값을 input의 개수를 루트 씌운 값으로 나누어서 사용함.
•
이 경우 그림 아래와 같이 layer가 지나도 적절한 분포가 유지된다.
•
input과 output에 대해 위와 같은 정의를 하면 최종적으로 분산은 가장 아래와 같은 식으로 표기할 수 있음
•
와 는 독립적이고, 와 는 identically distributed(같은 확률 분포) 하다는 가정 하에 분산을 아래와 같이 유도할 수 있음.
◦
이것을 통계학에서 i.i.d 추정이라고 한다. 한국 말로 ‘독립 항등 분포’라고 함. 어떤 랜덤 확률 변수의 집합이 있을 때 각각의 랜덤 확률변수들은 독립적이면서 동일한 분포를 가진다는 가정
•
이라는 가정을 추가하고 식을 유도하여 으로 정해주면 최종적으로 input와 output의 분산이 유사하다는 결론을 내릴 수 있음.
◦
몇가지 가정이 적용되었기 때문에 항상 옳지는 않지만, 대체로 적절한 값이 나온다.
•
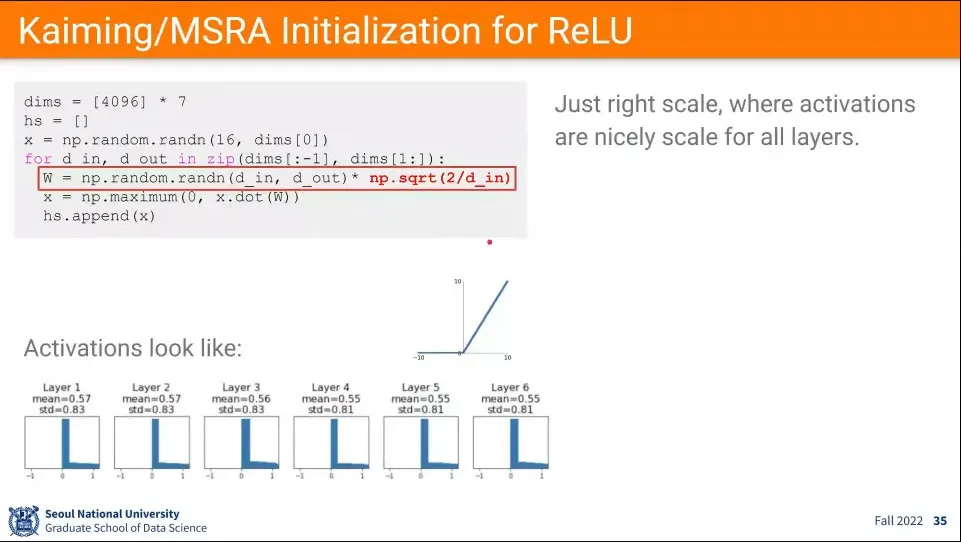
ReLU 함수에 대해서도 마찬가지 문제가 발생함. input이 0에 가까워지면 학습이 0에 수렴하는 문제.
•
이전과 비슷하게 ReLU에 대해서는 위와 같은 식을 적용하여 초기화 값을 사용함.
•
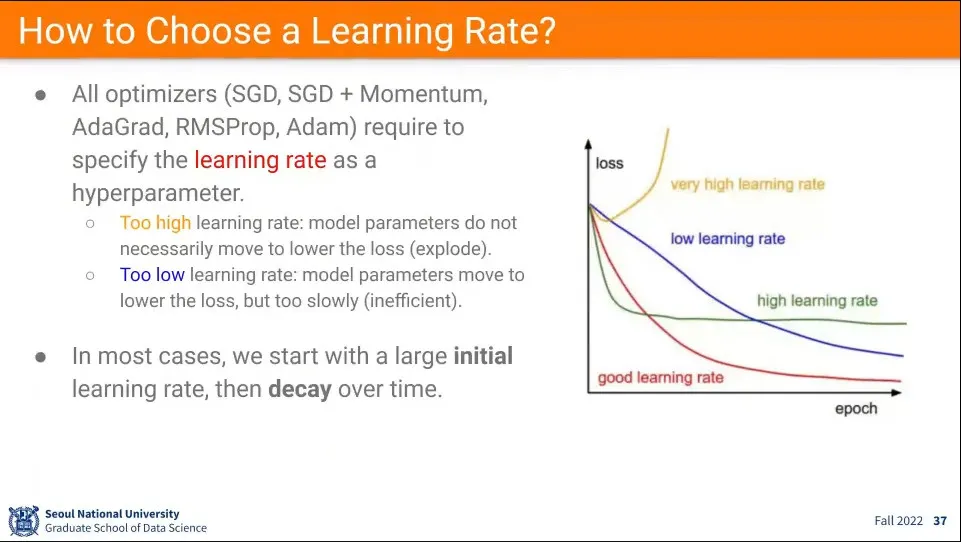
적절한 Learning rate를 선택하는 방법
◦
작으면 오래 걸리고, 크면 수렴이 안 된다. 너무 크면 수렴이 안 될 수도 있다.
•
일반적으로 처음에는 큰 값으로 초기화하고, 그 후에 점점 줄여가는 방법을 사용한다. 이렇게 하면 처음에는 빨리 내려가고, 그 후에 줄여가면서 계속 내려가게 할 수 있음.
◦
이것을 learing rate decay라고 함.
•
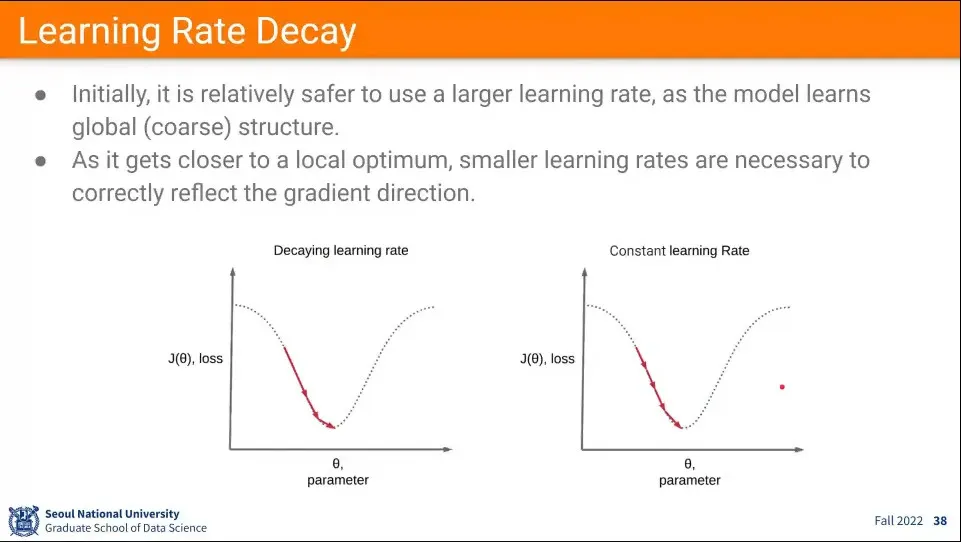
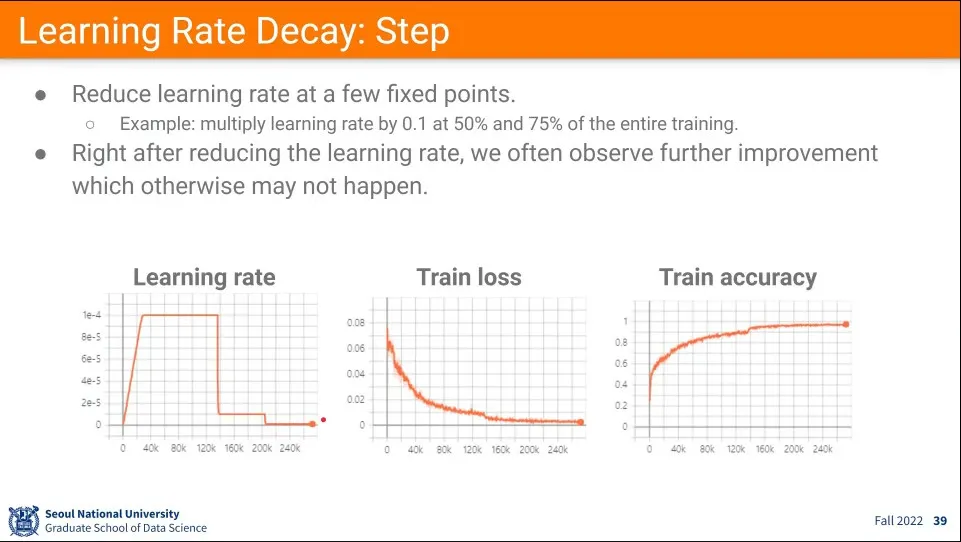
decay 하는 것이 고정된 learning rate를 쓰는 것보다 효과적이다.
•
learning rate을 줄여서 사용한 예
•
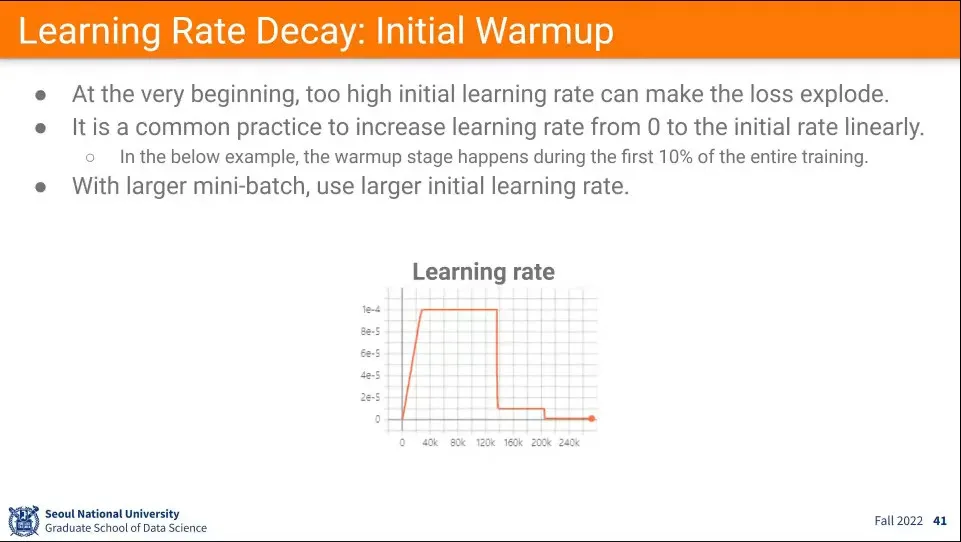
위 차트에서 learning rate를 처음부터 크게 주지 않고 작은 값에서 시작하고, 값을 키우는데 이것을 Initial Warmup이라고 한다.
•
추가로 mini-batch 크기에 맞춰서 learning rate를 조절해 주어야 한다.
◦
mini-batch가 2배가 되면 sum 하면서 값이 변동될 수 있음. 일반적으로 데이터들이 한방향으로 가지 않기 때문에 상쇄 효과로 batch 크기가 오히려 값이 안정적이 될 수 있음. 그래서 sum보다는 average를 써주는게 좋다.
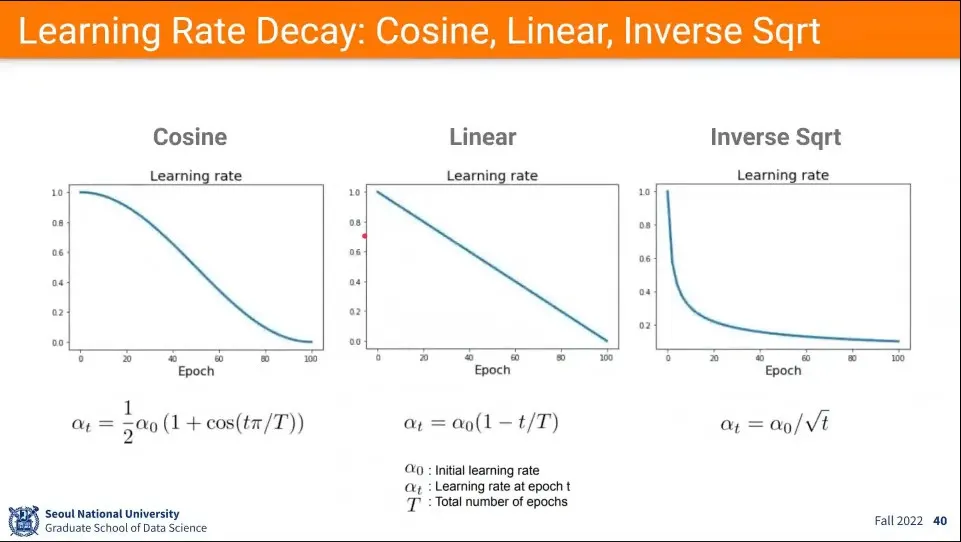
•
앞선 예에서 Learning Rate를 갑자기 줄였는데, 그렇게 안하고 위와 같이 몇가지 방법을 이용해서 점진적으로 사용할 수 있다.