1 Overview
fitting의 목표는 관찰된 데이터를 가장 잘 설명하는 파라메트릭 모델을 찾는 것이다. 우리는 데이터와 특정 모델 파라미터의 추정 사이의 선택된 fitting error를 최소화하여 그러한 모델의 최적의 파라미터를 얻는다. 전통적인 예는 주어진 점의 집합에 선을 fitting하는 것이다. 이 수업에서 본 다른 예는 서로 다른 이미지에 대응점들의 집합 사이의 2d homography 를 계산하거나 eight-point algorithm을 사용하여 fundamental matrix 를 계산하는 것이 있다.
2 Least-squares
개의 일련의 2d 점 가 주어지면, least-squares fitting의 방법은 차원의 제곱 에러가 최소화되도록 선 를 찾으려 한다. 그림 1 참조.
구체적으로 우리는 방정식 1에서 주어진 와 모델 추정치 사이의 squared residual의 합을 최소화하도록 하는 모델 파라미터 을 찾기를 원한다. 우리는 residual을 로 정의한다.
이것을 행렬 표기로 다음처럼 작성할 수 있다.
residual은 이제 이다. 우리는 가 skinny이고 full rank라고 가정한다. 우리는 residual squared의 norm을 최소화하는 를 찾기를 원한다. 이것은 다음처럼 작성할 수 있다.
그러면 에 대한 residual의 gradient를 으로 설정한다. 가 대칭임을 떠올려라.
이것은 normal equations를 이끈다.
이제 방정식 12에서 에 대한 닫힌 형식의 해를 갖는다. 는 full rank이므로 는 가역이다.
그러나 이 방법은 수직선(이 정의되지 않음)을 설명하는 점을 fitting하는데 완전히 실패하는 것에 유의하라. 이 경우에 은 매우 큰 수로 설정되어 수치적으로 불안정한 해를 이끈다. 이것을 해결하기 위해 형식의 대안 line formulation을 사용할 수 있다. 을 설정하면 수직선을 얻을 수 있다. 여기서 이 선 표현에 관한 생각을 하나 할 수 있다. 선 방향(slope)는 에 의해 주어지며, 를 만족하는 의 집합은 에 수직인 선이다. 그러나 선은 로 임의로 이동할 수 있다. 따라서 다음을 갖는다.
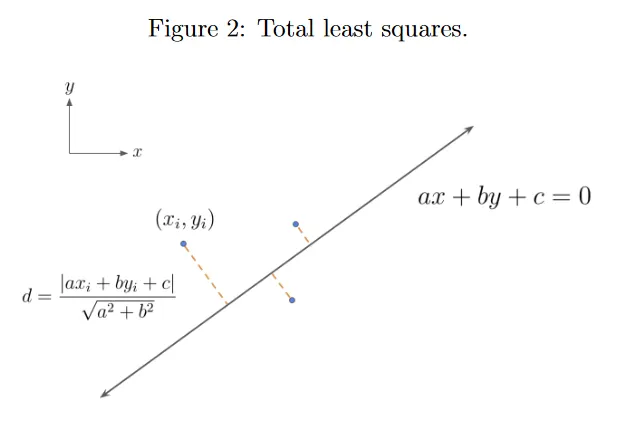
여기서 . 그러면 선의 기울기는 이다. 이것은 이제 정의되지 않을 수 있다. 이전에는 residual가 y축에만 있었지만 이제 새로운 선 파라미터화가 x와 y축 모두의 error를 고려하므로, 새로운 error는 squared orthogonal distance의 합이된다. 그림 2 참조.
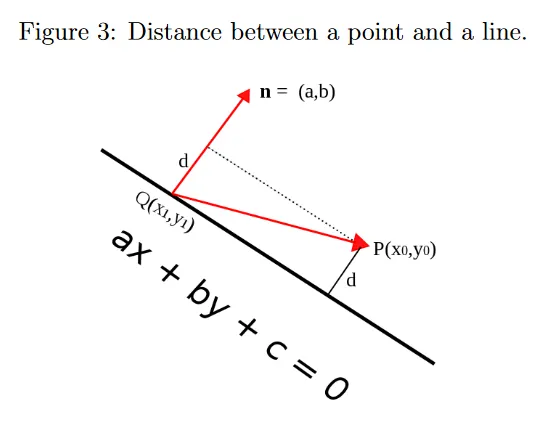
2d 데이터 포인트 와 선의 점 가 주어지면, 에서 선까지의 거리는 를 선에 수직인 normal vector(법선) 에 projection한 길이와 같다. 와 라 하면 다음과 같이 된다.
가 선 위에 놓인다는 것을 떠올려라. 따라서
이제 새로운 파라미터 집합은 이다. error를 단순화하기 위해 해를 고유하게 만들고 로 제한하여 분모를 제거한다. 따라서 새로운 에러는 다음과 같다.
여기서 . 그러나 제한이 에만 존재할 때 의 존재하기 때문에 이것을 행렬 표기로 놓는 것은 여전히 까다롭다. 더 간단히 하기 위해 를 최소화하는 best fit의 결과 선은 다음처럼 정의되는 데이터 centroid 를 통과해야 한다는 것에 유의하라.
모든 과 점의 모든 가능한 집합 에 대해 을 설정할 때 는 최소화된다. 즉 모든 점 가 주어지면 다음을 갖는다.
이것이 왜 사실인지 보기위해 다음과 같은 벡터 를 정의한다.
그러면 error를 다음과 같이 작성할 수 있다.
그러면 와 사이의 관계는
여기서 이고 은 값이 모두 1인 벡터이다. 가 에 직교하므로
따라서 피타고라스 정리에 의해 다음을 갖는다.
best fit의 선이 를 통과해야 함을 보았다. 따라서 를 다음과 같이 제약할 수 있다.
그러면 모든 점을 데이터 centroid 주위로 중심화되도록 이동하여(를 설정) 를 제거할 수 있다. 이를 통해 최종적으로 에러를 행렬 곱으로 형식화할 수 있다.
여기서 이고 . 이것은 이전 강의에서 보았던 제한된 least-squares 문제이다. SVD(full rank )에 의해 다음을 갖는다.
은 모두 orthonormal 행렬이다. 반면 은 의 singular 값을 내림차순으로 포함하는 대각 행렬이다. 여기서 이다. 가 직교이므로 다음을 안다.
를 설정하면 이제 새로운 제약조건 과 동등한 조건으로 를 최소화할 수 있다. 의 대각 항목이 내림차순으로 정렬되기 때문에 는 일 때 최소화된다. 마지막으로 를 얻으므로 error를 최소화하는 는 에서 마지막 열이다.
이득의 관점에서 해석하면 SVD 를 다음처럼 작성할 수 있다.
은 의 열이고 는 의 대각 값이고, 는 의 열이다. 를 SVD와 곱하면 가 되는데, 이것은 먼저 의 성분을 입력 방향 을 따라 계산하고, 로 성분을 scaling한 다음, 출력 방향 을 따라 재구성하는 것으로 볼 수 있다. 는 를 의 각 열을 따라 projection한 것이다(를 떠올려라). 유사하게 는 출력 방향의 선형 결합 으로 볼 수 있다. 따라서 제약 하에 를 최소화하는 를 찾는 것은 단순히 출력 벡터의 크기를 최소화하는 입력 방향을 선택하는 것이다. 이것은 의 마지막 열이다.
실제로 least-squares fitting은 noisy 데이터를 잘 다루지만 outlier에 취약하다. 왜 그런지 보기 위해 -번째 데이터 포인트에 대한 residual을 라 하고 비용을 라 작성하면, error를 다음으로 일반화할 수 있다.
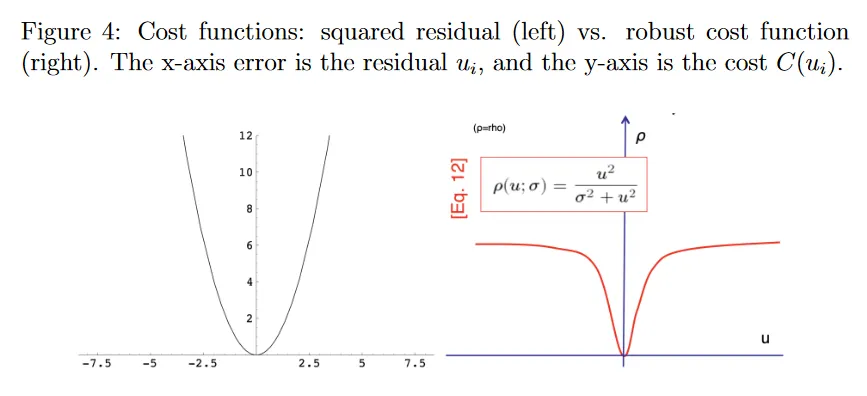
지금까지 사용한 제곱 에러 의 2차적 증가(그림 4의 왼쪽에 그려짐)는 큰 잔차 를 갖는 이상치가 비용 최소화에 지나치게 큰 영향을 미친다는 것을 의미한다.
다음과 같은 견고한 비용함수(그림 4의 오른쪽 절반)를 사용하여 큰 residuals(outliers)에 페널티를 부여할 수 있다.
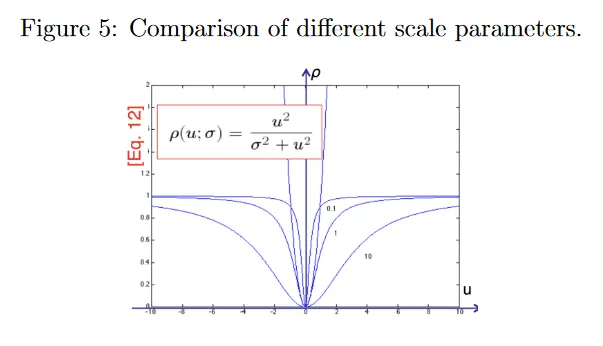
residual 가 클 때 비용 는 1로 saturate(포화)되어 비용에 대한 그들의 기여가 제한되지만, 가 작을 때는 비용함수는 squared error를 유사하다. 그러나 이제 scale parameter라 부르는 를 선택해야 한다. 는 잠재적 outlier에 가중치를 얼마나 부여할지를 제어한다. 그림 5 참조. 큰 는 중심의 2차 커브를 넓혀서, 다른 포인트에 대해 outlier에 상대적으로 더 페널티 부여한다(원래의 제곱 에러 함수와 유사하게). 작은 는 2차 커브를 좁혀, outlier에 대한 페널티 덜 부여한다. 가 너무 작으면 실제로 그렇지 않더라도 대부분의 residual가 outlier로 취급되어 빈곤한 fit을 이끈다. 가 너무 크면 견고한 비용 함수에서 이점을 얻지 못하고 결국 least-squares fit이 된다.
견고한 비용함수가 비선형이기 때문에 그들은 반복적 방법으로 최적화된다. 실제로 닫힌 형식 least-squares 해를 종종 시작점으로 사용한 다음, 견고한 비선형 비용 함수를 사용하여 파라미터를 반복적으로 fitting한다. 견고한 추정기에 대한 추가 디테일은 [HZ]에서 부록 6.8의 ‘Robust cost function’을 참조하라. 또한 이 노트에서 선에 대한 least-squares fitting을 유도했지만 [HZ]의 섹션 4.1에서는 동일한 least squares 최적화 절차를 사용하여 homography를 계산하는 direct linear transformation(DLT) algorithm을 간결하게 다룬다.
3 RANSAC
또 다른 fitting 방법은 RANSAC이다. 이것은 random sample consensus의 약자로 outlier와 missing 데이터에 견고하도록 설계되었다. RANSAC을 사용하여 여러 line fitting을 수행하는 방법을 보이지만 이는 다양한 fitting 맥락으로 일반화할 수 있다.
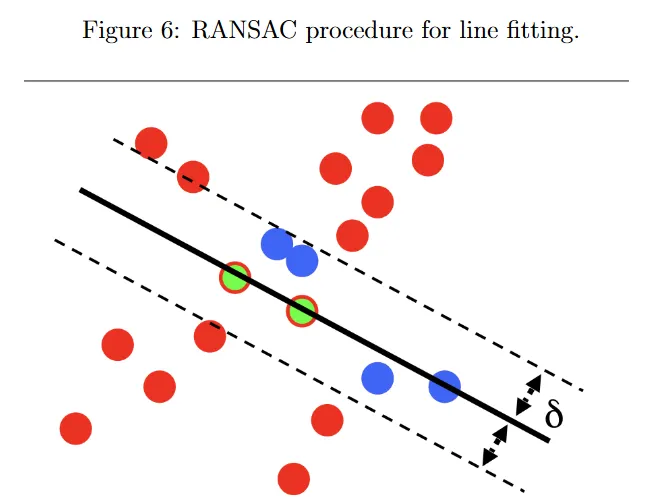
다시 개의 2d 점 집합 이 있고 여기에 line을 맞추기를 원한다고 하자. 그림 6 참조. RANSAC의 첫 번째 단계는 모델을 fit하는데 필요한 최소 수의 점을 랜덤으로 선택하는 것이다. 선에는 최소 2개 점이 필요하므로 녹색점 2개를 선택한다. 만일 fundamental 행렬 를 추정하면 eight-point algorithm을 사용하기 위해 8개의 대응점을 선택해야 한다. 만일 homography 을 계산하려면 scale까지 8개의 자유도를 다루기 위해 4개 대응점(각 대응점에 좌표 2개)이 필요하다. RANSAC에서 두 번째 단계는 랜덤 샘플 집합에 모델을 맞추는 것이다. 여기서 녹색점 2개에 선이 fit 되어(즉, 두 점 사이에 선이 그려진다) 검은색 선을 얻는다. 세 번째 단계는 fit 된 모델을 사용하여 전체 데이터셋에서 inlier set을 계산하는 것이다. 모델 파라미터 가 주어지면 inlier 집합을 로 정의한다. 여기서 은 데이터 포인트와 모델 사이의 residual이고 는 임의의 threshold이다. 여기서 inlier set은 녹색과 파란색 점으로 표현된다. inlier set의 크기 는 전체 점 집합 중 fit된 모델과 일치하는 정도를 표시한다. 를 사용하면 를 정의하여 outlier set을 얻을 수도 있다. 여기서 outlier set은 빨간색 점으로 표시된다. 우리는 inlier set의 크기가 최대화될 때까지 유한한 반복 횟수 동안 이 단계를 새로운 새로운 랜덤 샘플로 반복한다. RANSAC이 다양한 fitting 시나리오에 대해 간단하고 구현하기 쉽지만, 샘플 횟수 과 tolerance(허용) threshold 와 같은 몇 가지 파라미터를 조정해야 한다. RANSAC은 또한 좋은 모델에 동의하는 충분한 수의 inlier가 있다고 가정하며 파라미터를 계산하는 횟수에 대한 상한선이 없다(계산적으로 실현 가능하지 않은 경우 제외)
그러나 모든 가능한 샘플을 시도하는 것은 불필요하다. 주어진 (모델을 fit하는데 필요한 최소 점 수)와 (outlier 비율)에 대해 ‘real’ outlier’가 없는 inlier set을 갖는 최소 하나의 랜덤 샘플이 있을 확률 를 보장하는 반복 수 을 추정할 수 있다. 이제 개 점의 단일 랜덤 샘플이 모든 inlier를 포함할 확률은 이므로, 최소 하나의 outlier를 포함할 확률은 이다. 그러면 개의 모든 샘플이 최소 하나의 outlier를 포함할 확률은 이고, 개의 샘플 중 최소 하나가 outlier를 포함하지 않은 확률은 이다. 이제 을 로써 유도할 수 있다.
4 Hough transform
Hough transform이라는 또 다른 fitting 방법을 소개한다. 이것은 또 다른 voting 절차이다.
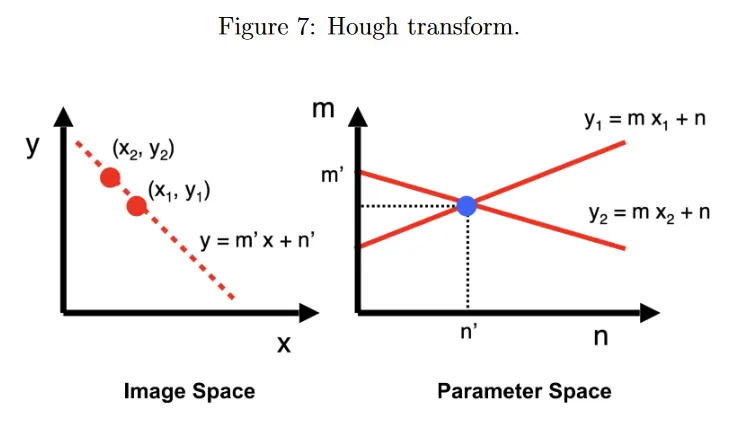
다시 형식의 선을 이미지에서 점의 시리즈 에 fit하기를 원한다고 하자. 그림 7의 왼쪽 절반 참조. 이 선을 찾기 위해 그림 7의 오른쪽 절반에 나온 dual parameter 또는 Hough space를 고려한다. 이미지 공간의 점 (선 상에 있음)는 으로 정의되는 파라미터 공간의 선이 된다. 유사하게 파라미터 공간에서 점 은 이미지 공간에서 으로 주어지는 선이 된다.
파라미터 공간의 선 는 이미지 공간의 점 를 통과하는 이미지 공간의 모든 가능한 선을 나타낸다. 따라서 이미지 공간의 점 과 를 모두 지나는 선을 찾으려면 두 점을 Hough space의 선과 연관시키고 교차점 을 찾는다. 이 Hough space의 점은 이미지 공간의 두 점을 모두 지나는 선을 나타낸다. 실제로 파라미터 공간에 대해 width 인 정사각형 셀로 이루어진 이산 grid로 Hough space를 나눈다. 초기에 모든 에 대해 을 중심으로 하는 셀의 갯수 격자 을 유지한다. 이미지 공간의 모든 데이터 포인트 에 대해 를 만족하는 모든 을 찾아 갯수를 1 증가시킨다. 모든 데이터 포인트에 대해 이 작업을 수행한 후에 Hough space에서 가장 높은 갯수를 가진 점 이 이미지 공간의 fit 된 선을 나타낸다. 이제 왜 이것이 voting 절차인지 알 수 있다. 각 데이터 요소 는 이미지 공간 각 후보 line 에 대해 최대 1표를 투표할 수 있다.
그러나 기존 파라미터화에 주요 한계가 있다. least-squares에서 논의한 것처럼 이미지 공간에서 선의 기울기는 로 unbounded이다. 이로 인해 Hough voting가 실제로는 계산과 메모리 집약 알고리즘이 되는데, 갯수를 유지 하는 파라미터 공간의 크기에 제한이 없기 때문이다. 이것을 해결하기 위해 그림 8에 나온 선의 polar 파라미터화를 사용한다.
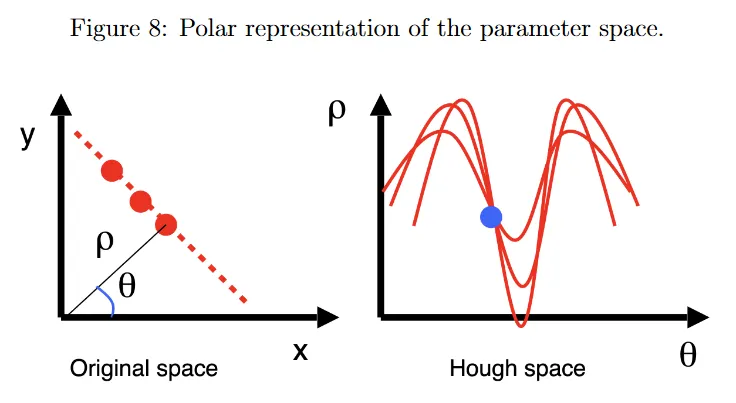
그림 8의 왼쪽 절반에서 가 원점에서 선까지의 최소 거리(이미지 크기 또는 데이터셋에서 임의의 두 점 사이의 최대 거리로 bound 됨)이고, 는 x축과 선의 normal vector 사이의 각도(0과 사이로 bound 됨)이다. 이전과 동일한 Hough voting 절차를 사용하지만 Cartesian space에서 특정한 를 지나는 모든 가능한 선은 이제 통해 Hough space에서 sinusoidal profile에 해당한다. 그림 8의 오른쪽 절반 참조.
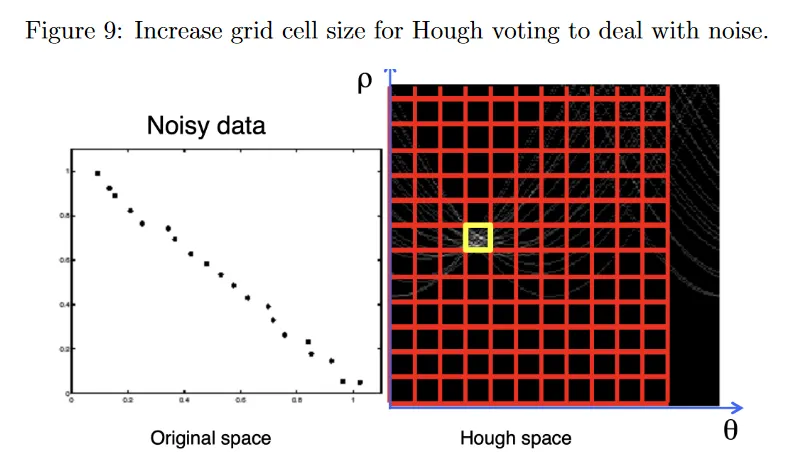
실제로 noisy 데이터 점은 이미지 공간에서 동일한 선 상의 점들에 해당하는 Hough space의 sinusoidal profile이 Hough space에서 반드시 동일한 점에서 교차하지 않을 수 있다. 이것을 해결하기 위해 그림 9에 나온 것처럼 grid cell의 width 를 증가시켜서 imperfect(불완전한) 교차점에 대한 tolerance(허용 오차)를 증가시킬 수 있다. 이렇게 하면 noisy 데이터를 다루는데 도움이 되지만 조정해야 하는 또 다른 파라미터가 생긴다. 작은 grid 크기는 noise 때문에 이미지 공간의 선을 놓칠 수 있는 반면, 큰 grid 크기는 모든 내의 셀이 가능한 선이기 때문에 다른 선을 병합하고 추정 정확도를 낮출 수 있다.
게다가 이미지 공간에 uniform noise가 존재하면, Hough space에 spurious(허위) peak가 존재할 수 있고 적절한 모델에 대한 명확한 consensus가 없게 된다.