Search
Duplicate

AI/ Article/ What are Diffusion Models

What are Diffusion Models?
[Updated on 2021-09-19: Highly recommend this blog post on score-based generative modeling by Yang Song (author of several key papers in the references)]. [Updated on 2022-08-27: Added classifier-free guidance, GLIDE, unCLIP and Imagen. [Updated on 2022-08-31: Added latent diffusion model. [Updated on 2024-04-13: Added progressive distillation, consistency models, and the Model Architecture section. So far, I’ve written about three types of generative models, GAN, VAE, and Flow-based models. They have shown great success in generating high-quality samples, but each has some limitations of its own.
https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
지금까지 GAN, VAE, Flow-Based 모델이라는 3가지 생성 모델에 관해 작성했다. 그것들은 높은 품질 샘플을 생성하는데 훌륭한 성공을 보였지만 각각 그 자체로 한계가 있다. GAN은 적대적 학습 특성 때문에 잠재적으로 불안정안 학습과 생성의 다양성이 적다. VAE는 surrogate loss에 의존하고 Flow 모델은 가역 변환을 구성하는 특수 아키텍쳐를 사용해야 한다.
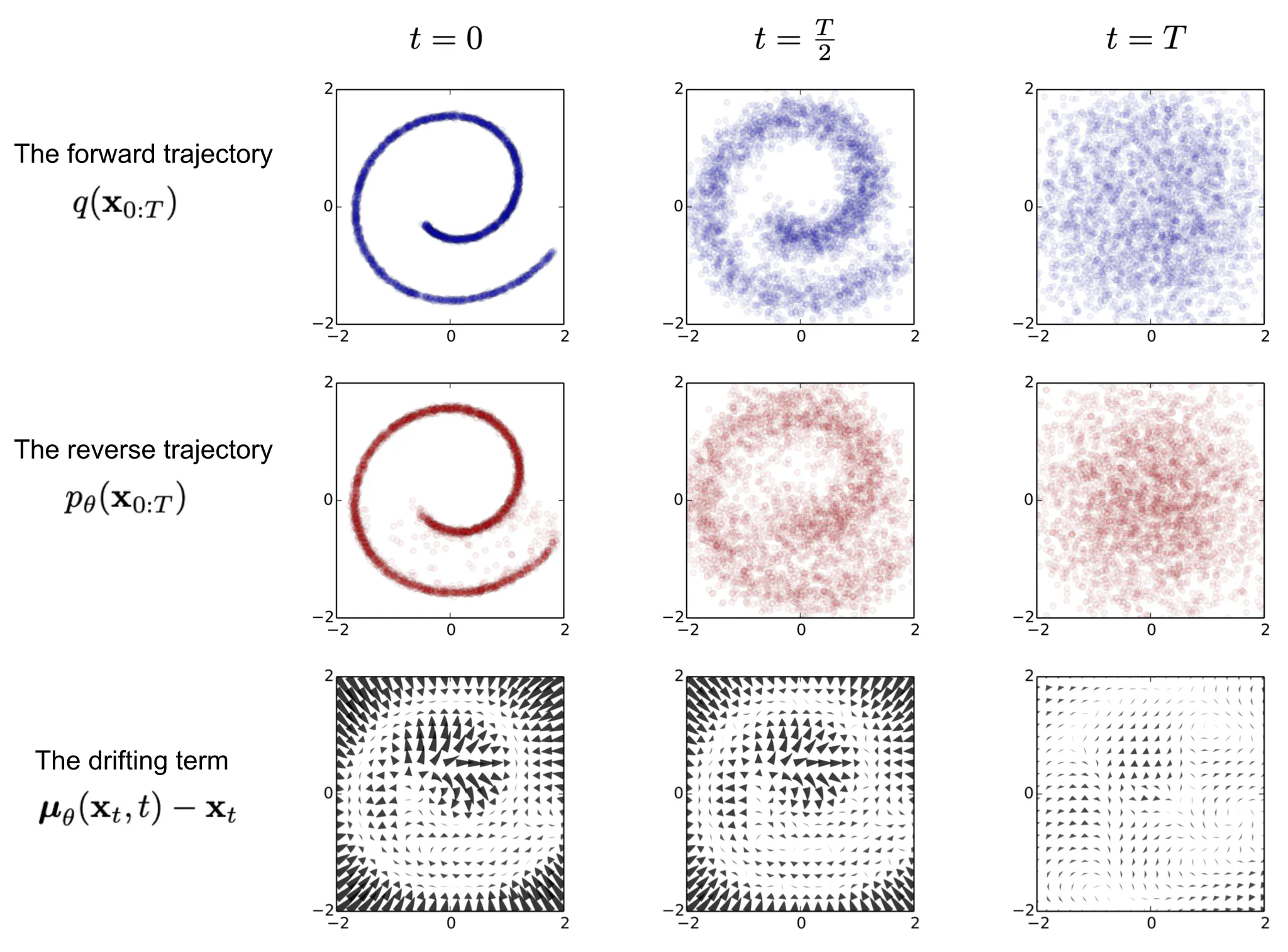
Diffusion 모델은 non-equilibrium thermodynamics(비평형 열역학)에 의해 영감을 받았다. 그들은 diffusion step의 Markov chain을 정의하여 데이터에 랜덤 노이즈를 천천히 추가한 다음 diffusion 절차를 역으로 학습하여 노이즈에서 원하는 데이터 샘플을 구성한다. VAE나 flow 모델과 다르게 diffusion model은 고정된 절차로 학습되고 잠재 변수는 높은 차원을 갖는다(원본 데이터와 같은)

What are Diffusion Models

여러 diffusion-based 생성 모델이 유사한 아이디어 아래 제안되었다. ‘diffusion probabilistic model’, ‘noise-conditioned score network(NCSN)’, ‘denoising diffusion probabilistic model(DDPM)’

Forward diffusion process

실제 데이터 분포 x0∼q(x)\mathbf{x}_0 \sim q(\mathbf{x})에서 샘플링된 데이터 포인트가 주어지면, TT 단계로 샘플에 소량의 가우스 노이즈를 추가하여 일련의 노이즈 샘플 x1,…,xT\mathbf{x}_1, \dots, \mathbf{x}_T 를 생성하는 forward diffusion process를 정의한다. step size는 분산 스케쥴 {βt∈(0,1)}t=1T\{\beta_t \in (0, 1)\}_{t=1}^T에 의해 제어됩니다.
q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)q(x1:T∣x0)=∏t=1Tq(xt∣xt−1)\begin{aligned} q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) &= \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}) \\ q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) &= \prod^T_{t=1} q(\mathbf{x}_t \vert \mathbf{x}_{t-1})\end{aligned}
step tt가 커짐에 따라 데이터 샘플 x0\mathbf{x}_0은 점차 구별가능한 특징을 잃게 됩니다. 결국 T→∞T \to \infty가 되면 xT\mathbf{x}_T는 isotropic Gaussian 분포와 동일해집니다.
위 프로세스의 좋은 특성은 reparameterization trick을 사용하여 닫힌 형식으로 모든 임의의 time step tt에서 xt\mathbf{x}_t를 샘플링할 수 있다는 것이다. αt=1−βt\alpha_t = 1 - \beta_t 와 αˉt=∏i=1tαi\bar{\alpha}_t = \prod_{i=1}^t \alpha_i라 하자.
xt=αtxt−1+1−αtϵt−1 ;where ϵt−1,ϵt−2,⋯∼N(0,I)=αtαt−1xt−2+1−αtαt−1ϵˉt−2 ;where ϵˉt−2 merges two Gaussians (*).=…=αˉtx0+1−αˉtϵq(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)\begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1} & \text{ ;where } \boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\boldsymbol{\epsilon}}_{t-2} & \text{ ;where } \bar{\boldsymbol{\epsilon}}_{t-2} \text{ merges two Gaussians (*).} \\ &= \dots \\ &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon} \\ q(\mathbf{x}_t \vert \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) \end{aligned}
(*) 분산이 다른 두 가우시안, N(0,σ12,I)\mathcal{N}(0, \sigma_1^2, I)과 N(0,σ22,I)\mathcal{N}(0, \sigma_2^2, I)을 병합하면 새로운 분포는 N(0,(σ12+σ22)I)\mathcal{N}(0, (\sigma_1^2 + \sigma_2^2)I)이 된다는 것을 떠올려라. 여기서 병합된 표준 편차는 (1−αt)+αt(1−αt−1)=1−αtαt−1\sqrt{(1 - \alpha_t) + \alpha_t (1-\alpha_{t-1})} = \sqrt{1 - \alpha_t\alpha_{t-1}}이다.
일반적으로 샘플의 노이즈거 커지면 더 큰 update step을 수행할 수 있다. 따라서 β1<β2<⋯<βT\beta_1 < \beta_2 < \dots < \beta_T이고 그러므로 αˉ1>⋯>αˉT\bar{\alpha}_1 > \dots > \bar{\alpha}_T이다.

Connection with stochastic gradient Langevin dynamics

Langevin Dynamics은 molecular systems(분자 시스템)을 통계적으로 모델링하기 위해 개발된 물리학의 개념입니다. stochastic gradient descent와 결합된 stochastic gradient Langevin dynamics은 Markov chain 업데이트에서 gradient ∇xlog⁡p(x)\nabla_\mathbf{x} \log p(\mathbf{x})만 사용하여 확률 밀도 p(x)p(\mathbf{x})에서 샘플을 생성할 수 있다.
xt=xt−1+δ2∇xlog⁡p(xt−1)+δϵt,where ϵt∼N(0,I)\mathbf{x}_t = \mathbf{x}_{t-1} + \frac{\delta}{2} \nabla_\mathbf{x} \log p(\mathbf{x}_{t-1}) + \sqrt{\delta} \boldsymbol{\epsilon}_t ,\quad\text{where } \boldsymbol{\epsilon}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{I})
여기서 δ\delta는 step size이다. T→∞,ϵ→0T \to \infty, \epsilon \to 0 일 때, xT\mathbf{x}_T는 실제 확률 밀도 p(x)p(\mathbf{x})와 같아진다.
표준 SGD과 비교하여 stochastic gradient Langevin dynamics는 가우시안 노이즈를 파라미터 업데이트에 주입하여 local minima로 붕괴하는 것을 피한다.

Reverse diffusion process

위의 절차를 반전하고 q(xt−1∣xt)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)에서 샘플을 추출할 수 있다면 가우시안 노이즈 입력 xT∼N(0,I)\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})에서 실제 샘플을 재생성할 수 있다. 만일 βt\beta_t가 충분히 작으면 q(xt−1∣xt)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)도 가우시안이 된다는 점에 유의하라.
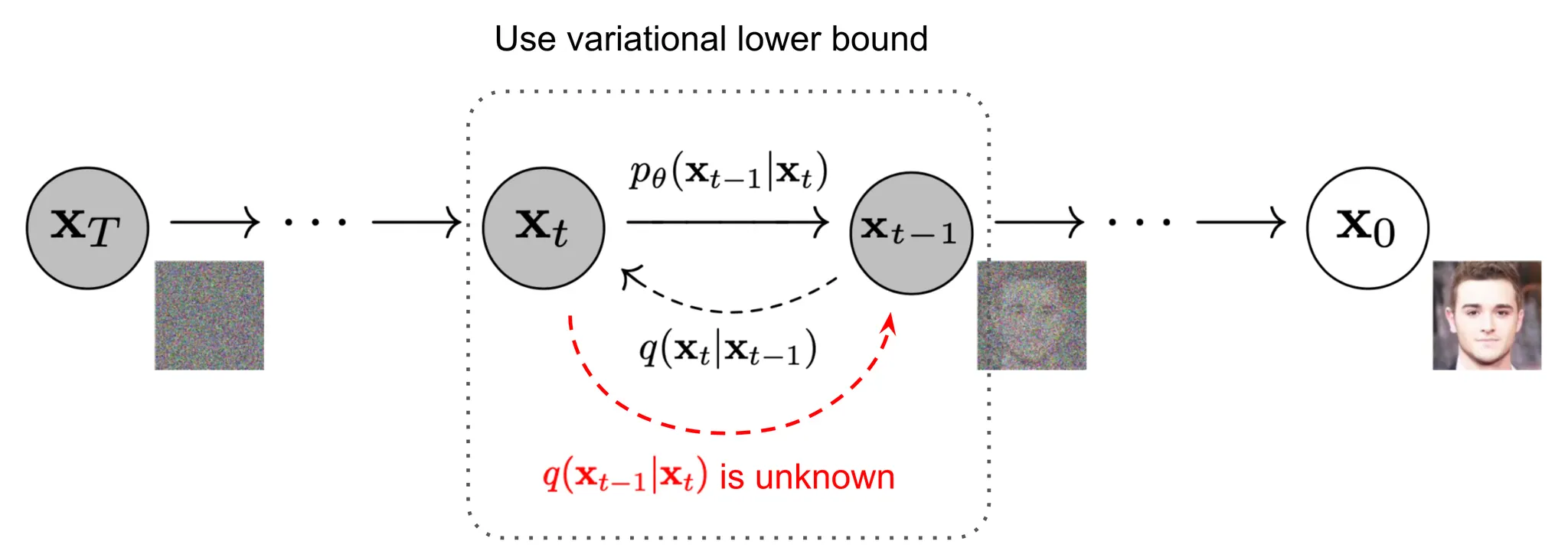
불행히 전체 데이터셋을 사용해야 하기 때문에 q(xt−1∣xt)q(x_{t-1}|x_t)를 쉽게 추정할 수 없다. 그러므로 reverse diffusion 프로세스를 실행하기 위해 이 조건부 확률을 근사하도록 모델 pθp_\theta을 학습해야 한다.
pθ(x0:T)=p(xT)∏t=1Tpθ(xt−1∣xt)pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))\begin{aligned} p_\theta(\mathbf{x}_{0:T}) &= p(\mathbf{x}_T) \prod^T_{t=1} p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \\ p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) &= \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) \end{aligned}
x0\mathbf{x}_0에 조건화될 때 reverse 조건부 확률이 다루기 쉬워진다는 점에 주목할 가치가 있다.
q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \color{blue}{\tilde{\boldsymbol{\mu}}}(\mathbf{x}_t, \mathbf{x}_0), \color{red}{\tilde{\beta}_t} \mathbf{I})
베이지안 룰을 사용해서
q(xt−1∣xt,x0) =q(xt∣xt−1,x0)q(xt−1∣x0)q(xt∣x0)∝exp⁡(−12((xt−αtxt−1)2βt+(xt−1−αˉt−1x0)21−αˉt−1−(xt−αˉtx0)21−αˉt))=exp⁡(−12(xt2−2αtxtxt−1+αtxt−12βt+xt−12−2αˉt−1x0xt−1+αˉt−1x02 1−αˉt−1−(xt−αˉtx0)21−αˉt))=exp⁡(−12((αtβt+11−αˉt−1)xt−12−(2αtβtxt+2αˉt−11−αˉt−1x0)xt−1+C(xt,x0)))\begin{aligned}q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \\&\propto \exp \Big(-\frac{1}{2} \big(\frac{(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2}{\beta_t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\&= \exp \Big(-\frac{1}{2} \big(\frac{\mathbf{x}_t^2 - 2\sqrt{\alpha_t} \mathbf{x}_t \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \alpha_t} \color{red}{\mathbf{x}_{t-1}^2} }{\beta_t} + \frac{ \color{red}{\mathbf{x}_{t-1}^2} \color{black}{- 2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0} \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \bar{\alpha}_{t-1} \mathbf{x}_0^2}  }{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\&= \exp\Big( -\frac{1}{2} \big( \color{red}{(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})} \mathbf{x}_{t-1}^2 - \color{blue}{(\frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)} \mathbf{x}_{t-1} \color{black}{ + C(\mathbf{x}_t, \mathbf{x}_0) \big) \Big)}\end{aligned}
여기서 C(xt,x0)C(x_t, x_0)는 xt−1x_{t-1}를 포함하지 않는 함수이고 자세한 설명은 생략합니다. 표준 가우스 밀도 함수에 따라 평균과 분산을 다음과 같이 파라미터화 할 수 있습니다 (αt=1−βt\alpha_t = 1 - \beta_t와 αˉt=∏i=1Tαi\bar{\alpha}_t = \prod_{i=1}^T \alpha_i):
β~t =1/(αtβt+11−αˉt−1) =1/(αt−αˉt+βtβt(1−αˉt−1))=1−αˉt−11−αˉt⋅βtμ~t(xt,x0)=(αtβtxt+αˉt−11−αˉt−1x0)/(αtβt+11−αˉt−1)=(αtβtxt+αˉt−11−αˉt−1x0)1−αˉt−11−αˉt⋅βt=αt(1−αˉt−1)1−αˉtxt+αˉt−1βt1−αˉtx0\begin{aligned}\tilde{\beta}_t &= 1/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) = 1/(\frac{\alpha_t - \bar{\alpha}_t + \beta_t}{\beta_t(1 - \bar{\alpha}_{t-1})})= \color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\\tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \mathbf{x}_0)&= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) \\&= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0) \color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\&= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\\\end{aligned}
nice property 덕분에 x0=1αˉt(xt−1−αˉtϵt)\mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t)을 표현할 수 있고 위의 방정식에 연결하여 다음과 같은 결과를 얻을 수 있습니다:
μ~t=αt(1−αˉt−1)1−αˉtxt+αˉt−1βt1−αˉt1αˉt(xt−1−αˉtϵt)=1αt(xt−1−αt1−αˉtϵt)\begin{aligned}\tilde{\boldsymbol{\mu}}_t&= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t) \\&= \color{cyan}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)}\end{aligned}
그림 2에서 볼 수 있듯이 이러한 설정은 VAE와 매우 유사하고 따라서 variational lower bound(VLB)를 사용하여 negative log-likelihood를 최적화할 수 있다.
−log⁡pθ(x0) ≤−log⁡pθ(x0)+DKL(q(x1:T∣x0)∥pθ(x1:T∣x0))=−log⁡pθ(x0)+Ex1:T∼q(x1:T∣x0)[log⁡q(x1:T∣x0)pθ(x0:T)/pθ(x0)]=−log⁡pθ(x0)+Eq[log⁡q(x1:T∣x0)pθ(x0:T)+log⁡pθ(x0)]=Eq[log⁡q(x1:T∣x0)pθ(x0:T)]Let LVLB =Eq(x0:T)[log⁡q(x1:T∣x0)pθ(x0:T)]≥−Eq(x0)log⁡pθ(x0)\begin{aligned}- \log p_\theta(\mathbf{x}_0) &\leq - \log p_\theta(\mathbf{x}_0) + D_\text{KL}(q(\mathbf{x}_{1:T}\vert\mathbf{x}_0) \| p_\theta(\mathbf{x}_{1:T}\vert\mathbf{x}_0) ) \\&= -\log p_\theta(\mathbf{x}_0) + \mathbb{E}_{\mathbf{x}_{1:T}\sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T}) / p_\theta(\mathbf{x}_0)} \Big] \\&= -\log p_\theta(\mathbf{x}_0) + \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} + \log p_\theta(\mathbf{x}_0) \Big] \\&= \mathbb{E}_q \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\\text{Let }L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \geq - \mathbb{E}_{q(\mathbf{x}_0)} \log p_\theta(\mathbf{x}_0)\end{aligned}
Jensen의 부등식을 사용하여 동일한 결과를 얻는 것도 간단하다. 학습 목적으로 cross entropy를 최소화하기를 원한다고 가정하자.
LCE=−Eq(x0)log⁡pθ(x0)=−Eq(x0)log⁡(∫pθ(x0:T)dx1:T)=−Eq(x0)log⁡(∫q(x1:T∣x0)pθ(x0:T)q(x1:T∣x0)dx1:T)=−Eq(x0)log⁡(Eq(x1:T∣x0)pθ(x0:T)q(x1:T∣x0))≤−Eq(x0:T)log⁡pθ(x0:T)q(x1:T∣x0)=Eq(x0:T)[log⁡q(x1:T∣x0)pθ(x0:T)]=LVLB\begin{aligned}L_\text{CE}&= - \mathbb{E}_{q(\mathbf{x}_0)} \log p_\theta(\mathbf{x}_0) \\&= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \int p_\theta(\mathbf{x}_{0:T}) d\mathbf{x}_{1:T} \Big) \\&= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \int q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} d\mathbf{x}_{1:T} \Big) \\&= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \mathbb{E}_{q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} \Big) \\&\leq - \mathbb{E}_{q(\mathbf{x}_{0:T})} \log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} \\&= \mathbb{E}_{q(\mathbf{x}_{0:T})}\Big[\log \frac{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})}{p_\theta(\mathbf{x}_{0:T})} \Big] = L_\text{VLB}\end{aligned}
방정식의 각 항을 해석적으로 계산할 수 있도록 변환하기 위해 목적을 몇몇 KL divergence와 entropy 항의 결합으로 재작성할 수 있다.(자세한 단계별 프로세스는 부록 B의 Sohl-Dickstein et al., 2015 참조):
LVLB =Eq(x0:T)[log⁡q(x1:T∣x0)pθ(x0:T)]=Eq[log⁡∏t=1Tq(xt∣xt−1)pθ(xT)∏t=1Tpθ(xt−1∣xt)]=Eq[−log⁡pθ(xT)+∑t=1Tlog⁡q(xt∣xt−1)pθ(xt−1∣xt)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡q(xt∣xt−1)pθ(xt−1∣xt)+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡(q(xt−1∣xt,x0)pθ(xt−1∣xt)⋅q(xt∣x0)q(xt−1∣x0))+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡q(xt−1∣xt,x0)pθ(xt−1∣xt)+∑t=2Tlog⁡q(xt∣x0)q(xt−1∣x0)+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡q(xt−1∣xt,x0)pθ(xt−1∣xt)+log⁡q(xT∣x0)q(x1∣x0)+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[log⁡q(xT∣x0)pθ(xT)+∑t=2Tlog⁡q(xt−1∣xt,x0)pθ(xt−1∣xt)−log⁡pθ(x0∣x1)]=Eq[DKL(q(xT∣x0)∥pθ(xT))⏟LT+∑t=2TDKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))⏟Lt−1−log⁡pθ(x0∣x1)⏟L0]\begin{aligned}L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\&= \mathbb{E}_q \Big[ \log\frac{\prod_{t=1}^T q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{ p_\theta(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) } \Big] \\&= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=1}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} \Big] \\&= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\&= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \Big( \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)}\cdot \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1}\vert\mathbf{x}_0)} \Big) + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\&= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1} \vert \mathbf{x}_0)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\&= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{q(\mathbf{x}_1 \vert \mathbf{x}_0)} + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big]\\&= \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_T)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \Big] \\&= \mathbb{E}_q [\underbrace{D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))}_{L_T} + \sum_{t=2}^T \underbrace{D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t))}_{L_{t-1}} \underbrace{- \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} ]\end{aligned}
variational lower bound 손실에서 각 성분을 개별적으로 라벨링 해보자.
LVLB=LT+LT−1+⋯+L0where LT=DKL(q(xT∣x0)∥pθ(xT))Lt=DKL(q(xt∣xt+1,x0)∥pθ(xt∣xt+1)) for 1≤t≤T−1L0=−log⁡pθ(x0∣x1)\begin{aligned}L_\text{VLB} &= L_T + L_{T-1} + \dots + L_0 \\\text{where } L_T &= D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T)) \\L_t &= D_\text{KL}(q(\mathbf{x}_t \vert \mathbf{x}_{t+1}, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_t \vert\mathbf{x}_{t+1})) \text{ for }1 \leq t \leq T-1 \\L_0 &= - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)\end{aligned}
LVLBL_\text{VLB}의 모든 KL 항(L0L_0 제외)은 두 가우시안 분포를 비교하므로 닫힌 형식으로 계산할 수 있다. qq가 학습 가능한 파라미터를 갖지 않고 xT\mathbf{x}_T가 가우시안 노이즈이므로 LTL_{T}는 상수이고 학습하는 동안 무시할 수 있다. Ho et al. 2020은 N(x0;μθ(x1,1),Σθ(x1,1))\mathcal{N}(\mathbf{x}_0; \boldsymbol{\mu}_\theta(\mathbf{x}_1, 1), \boldsymbol{\Sigma}_\theta(\mathbf{x}_1, 1))에서 유도된 분리 이산 디코더를 사용하여 L0L_{0}을 모델링합니다. .

Parameterization of LtL_t for Training Loss

reverse diffusion 프로세스 pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))에서 조건화된 확률 분포를 근사하도록 신경망을 학습해야 한다는 것을 떠올려라. μθ\boldsymbol{\mu}_\theta을 훈련하여 μ~t=1αt(xt−1−αt1−αˉtϵt)\tilde{\boldsymbol{\mu}}_t = \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)를 예측하기를 원한다.
훈련 시간에 xt\mathbf{x}_t를 입력으로 사용할 수 있으므로 대신 가우시안 노이즈 항을 재파라미터화 하여 시간 단계 tt에서 입력 xt\mathbf{x}_t로부터 ϵt\boldsymbol{\epsilon}_t를 예측하도록 할 수 있다.
μθ(xt,t)=1αt(xt−1−αt1−αˉtϵθ(xt,t))Thus xt−1=N(xt−1;1αt(xt−1−αt1−αˉtϵθ(xt,t)),Σθ(xt,t))\begin{aligned}\boldsymbol{\mu}_\theta(\mathbf{x}_t, t) &= \color{cyan}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big)} \\\text{Thus }\mathbf{x}_{t-1} &= \mathcal{N}(\mathbf{x}_{t-1}; \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))\end{aligned}
손실 항 LtL_t는 μ~\tilde{\boldsymbol{\mu}}에서 차이를 최소화 하도록 파라미터화됩니다. :
Lt =Ex0,ϵ[12∥Σθ(xt,t)∥22∥μ~t(xt,x0)−μθ(xt,t)∥2]=Ex0,ϵ[12 ∥Σθ∥22∥1αt(xt−1−αt1−αˉtϵt)−1αt(xt−1−αt1−αˉtϵθ(xt,t))∥2]=Ex0,ϵ[(1−αt)22αt(1−αˉt)∥Σθ∥22∥ϵt−ϵθ(xt,t)∥2]=Ex0,ϵ[(1−αt)22αt(1−αˉt)∥Σθ∥22∥ϵt−ϵθ(αˉtx0+1−αˉtϵt,t)∥2] \begin{aligned}L_t &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \| \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) \|^2_2} \| \color{blue}{\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - \color{green}{\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2 \Big] \\&= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2  \|\boldsymbol{\Sigma}_\theta \|^2_2} \| \color{blue}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} - \color{green}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) \Big)} \|^2 \Big] \\&= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\&= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}

Simplification

Ho 등(2020)은 가중치 항을 무시하는 단순화된 목적의 diffusion 모델을 학습하는 것이 더 낫다는 것을 경험적으로 발견했다.
Ltsimple=Et∼[1,T],x0,ϵt[∥ϵt−ϵθ(xt,t)∥2]=Et∼[1,T],x0,ϵt[∥ϵt−ϵθ(αˉtx0+1−αˉtϵt,t)∥2]\begin{aligned}L_t^\text{simple}&= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\&= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big]\end{aligned}
최종 단순한 목적은 다음과 같다.
Lsimple=Ltsimple+CL_\text{simple} = L_t^\text{simple} + C
여기서 CC는 θ\theta에 의존하지 않는 상수입니다. .

Connection with noise-conditioned score networks (NCSN)

Song & Ermon(2019)은 score-based 생성 모델링 방법을 제안했다. 여기서 샘플은 score matching을 사용하여 추정된 데이터 분포의 gradient를 사용하는 Langevin dynamics를 통해 생성된다. 각 샘플 x\mathbf{x}의 밀도 확률의 score는 그것의 gradient ∇xlog⁡q(x)\nabla_{\mathbf{x}} \log q(\mathbf{x})로 정의된다. score 네트워크 sθ:RD→RD\mathbf{s}_\theta: \mathbb{R}^D \to \mathbb{R}^D는 sθ(x)≈∇xlog⁡q(x)\mathbf{s}_\theta(\mathbf{x}) \approx \nabla_{\mathbf{x}} \log q(\mathbf{x})을 추정하도록 학습된다.
이것을 딥러닝 설정에서 고차원 데이터로 확장하기 위해 그들은 denoising score matching(Vincent, 2011)이나 sliced score matching(랜덤 projection을 사용. Song et al. 2019)을 사용할 것을 제안했다. Denoising score matching은 미리 지정된 작은 노이즈를 q(x~∣x)q(\tilde{\mathbf{x}} \vert \mathbf{x})에 추가하고 score matching을 사용하여 q(x~)q(\tilde{\mathbf{x}})을 추정한다.
Langevin dynamics가 반복적인 절차에서 score ∇xlog⁡q(x)\nabla_{\mathbf{x}} \log q(\mathbf{x})만 사용하여 확률 밀도 분포에서 데이터 포인트를 샘플링할 수 있다는 점을 떠올려라.
그러나 manifold 가설에 따르면, 관찰된 데이터가 임의의 고차원으로 보이더라도 데이터의 대부분은 저차원 manifold에 집중될 것으로 예상된다. 이는 데이터 포인트가 전체 공간을 커버할 수 없기 때문에 score 추정에 부정적인 영향을 미친다. 데이터 밀도가 낮은 region에서 score 추정은 덜 신뢰할만 하다. 교란된 데이터 분포가 커버하는 전체 공간 RD\mathbb{R}^D을 만들기 위해 작은 가우시안 노이즈를 추가한 후에 score 추정 네트워크의 학습은 더 안정적이 된다. Song & Ermon (2019)은 다양한 수준의 잡음으로 데이터를 교란하고 노이즈 조건화된 score 네트워크를 학습하여 다양한 노이즈 레벨에서 모든 교란된 데이터의 score를 결합으로 추정함으로써 이를 개선했다.
노이즈 레벨을 증가시키는 스케쥴은 forward diffusion 프로세스과 유사하다. diffusion 프로세스 주석을 사용하면 score를 근사할 수 있다. sθ(xt,t)≈∇xtlog⁡q(xt)\mathbf{s}_\theta(\mathbf{x}_t, t) \approx \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t). 가우시안 분포 x∼N(μ,σ2I)\mathbf{x} \sim \mathcal{N}(\mathbf{\mu}, \sigma^2 \mathbf{I})가 주어지면 그것의 밀도 함수의 log의 도함수를 ∇xlog⁡p(x)=∇x(−12σ2(x−μ)2)=−x−μσ2=−ϵσ\nabla_{\mathbf{x}}\log p(\mathbf{x}) = \nabla_{\mathbf{x}} \Big(-\frac{1}{2\sigma^2}(\mathbf{x} - \boldsymbol{\mu})^2 \Big) = - \frac{\mathbf{x} - \boldsymbol{\mu}}{\sigma^2} = - \frac{\boldsymbol{\epsilon}}{\sigma}로 작성할 수 있다. 여기서 ϵ∼N(0,I)\boldsymbol{\epsilon} \sim \mathcal{N}(\boldsymbol{0}, \mathbf{I}). q(xt∣x0)∼N(αˉtx0,(1−αˉt)I)q(\mathbf{x}_t \vert \mathbf{x}_0) \sim \mathcal{N}(\sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I})임을 떠올려라. 그러므로
sθ(xt,t)≈∇xtlog⁡q(xt)=Eq(x0)[∇xtq(xt∣x0)]=Eq(x0)[−ϵθ(xt,t)1−αˉt]=−ϵθ(xt,t)1−αˉt\begin{aligned} \mathbf{s}_\theta(\mathbf{x}_t, t) \approx \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) &= \mathbb{E}_{q(\mathbf{x}_0)} [\nabla_{\mathbf{x}_t} q(\mathbf{x}_t \vert \mathbf{x}_0)] \\&= \mathbb{E}_{q(\mathbf{x}_0)} \Big[ - \frac{\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)}{\sqrt{1 - \bar{\alpha}_t}} \Big] = - \frac{\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)}{\sqrt{1 - \bar{\alpha}_t}} \end{aligned}

Parameterization of βt\beta_t

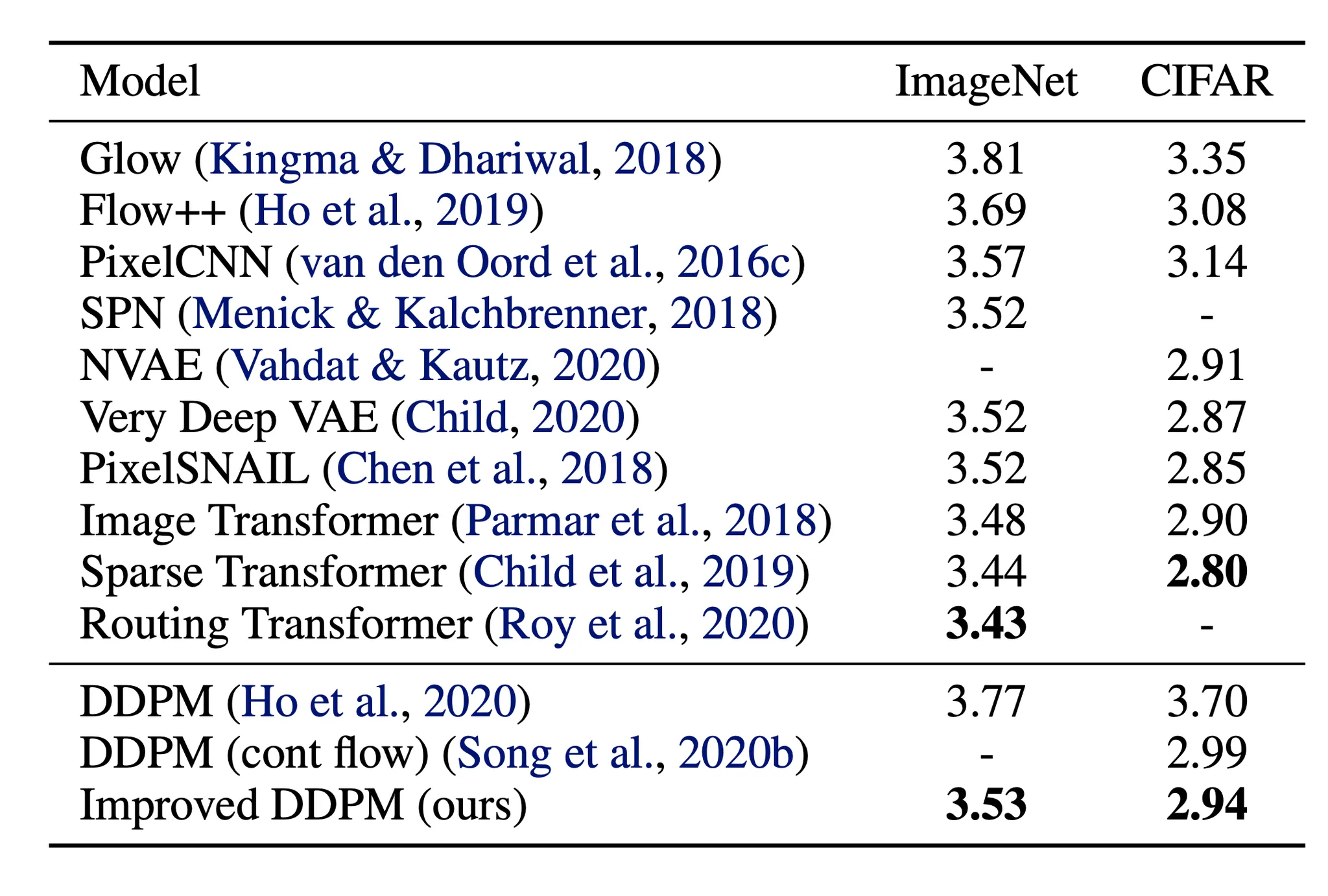
Ho et al. (2020)에서 forward 분산은 선형으로 증가하는 상수의 시퀀스로 설정된다. β1=10−4\beta_1=10^{-4}에서 βT=0.02\beta_T=0.02까지이다. 이것은 [−1,1][-1, 1] 사이로 정규화된 이미지 픽셀 값에 비해 상대적으로 작다. 그들의 실험에서 Diffusion 모델은 높은 품질의 샘플을 보였지만 여전히 다른 생성 모델만큼 경쟁력 있는 모델 log-likelihood를 달성하지 못했다.
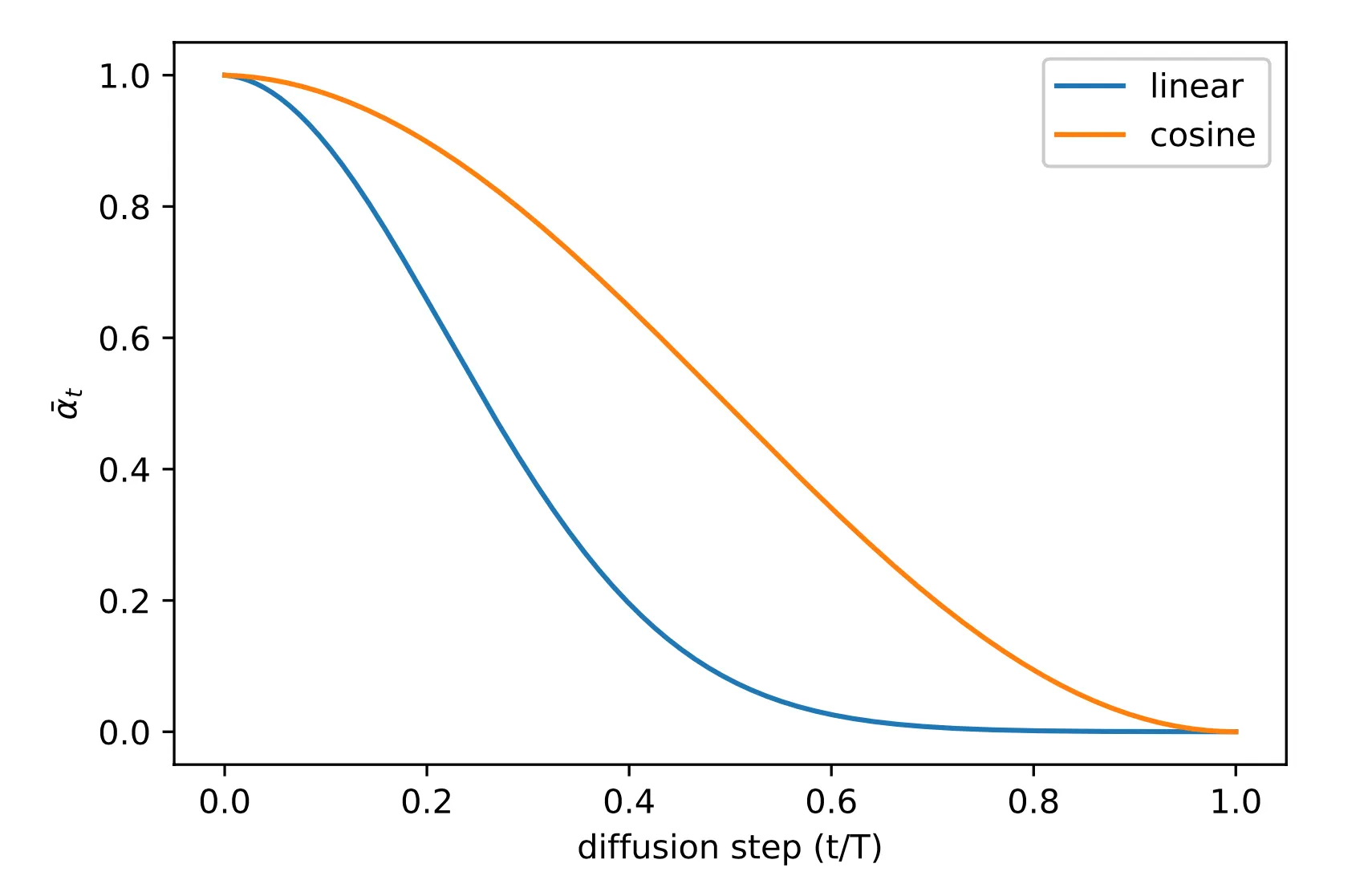
Nichol & Dhariwal(2021)은 확산 모델이 더 낮은 NLL을 얻는 데 도움이 되는 몇 가지 개선 기법을 제안했다. 개선 사항 중 하나는 cosine 기반 분산 스케줄을 사용하는 것입니다. 스케줄링 함수의 선택은 학습 프로세스의 중간에 선형에 가깝게 하락하고 t=0t=0과 t=Tt=T 근처에서 미묘한 변화를 제공하는 한 임의적일 수 있다.
βt=clip(1−αˉtαˉt−1,0.999)αˉt=f(t)f(0)where f(t)=cos⁡(t/T+s1+s⋅π2)2\beta_t = \text{clip}(1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}, 0.999) \quad\bar{\alpha}_t = \frac{f(t)}{f(0)}\quad\text{where }f(t)=\cos\Big(\frac{t/T+s}{1+s}\cdot\frac{\pi}{2}\Big)^2
여기서 작은 오프셋 ss는 t=0t=0에 가까울 때 βt\beta_t가 너무 작아지는 것을 방지하기 위한 것입니다. .
[그림] 훈련 중 βt\beta_t의 선형 기반 스케줄링과 코사인 기반 스케줄링 비교. (이미지 출처: Nichol & Dhariwal, 2021)

Parameterization of reverse process variance Σθ\Sigma_\theta

Ho et al. (2020)은 βt\beta_t를 학습 가능하게 하는 대신 상수로 고정하고 Σθ(xt,t)=σt2I\boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) = \sigma^2_t \mathbf{I}를 설정했다. 여기서 σt\sigma_t는 학습되지 않고 βt\beta_t 또는 β~t=1−αˉt−11−αˉt⋅βt\tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t로 설정한다. 대각 분산 Σθ\boldsymbol{\Sigma}_\theta를 학습하는 것이 학습이 불안정하게 하고 샘플 품질이 저하된다는 사실을 발견했기 때문이다.
Nichol & Dhariwal (2021)은 혼합 벡터 v\mathbf{v}를 예측하는 모델을 통해 βt\beta_t과 β~t\tilde{\beta}_t 사이의 보간으로 Σθ(xt,t)\boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)를 학습할 것을 제안했습니다:
Σθ(xt,t)=exp⁡(vlog⁡βt+(1−v)log⁡β~t)\boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) = \exp(\mathbf{v} \log \beta_t + (1-\mathbf{v}) \log \tilde{\beta}_t)
그러나 단순 목적 LsimpleL_\text{simple}은 Σθ\boldsymbol{\Sigma}_\theta에 종속되지 않습니다. 종속성을 추가하기 위해 그들은 혼합 목적 Lhybrid=Lsimple+λLVLBL_\text{hybrid} = L_\text{simple} + \lambda L_\text{VLB}을 구성했다. 여기서 λ=0.001\lambda=0.001는 작고 LVLBL_\text{VLB} 항에서 μθ\boldsymbol{\mu}_\theta에 대한 gradient를 중지하여 LVLBL_\text{VLB}가 Σθ\boldsymbol{\Sigma}_\theta의 학습만 유도하도록 했다. 경험적으로 그들은 noisy gradient 때문에 LVLBL_\text{VLB}를 최적화하는 것이 꽤 어렵다는 것을 관찰했고, 따라서 importance sampling을 통해 LVLBL_\text{VLB}의 time-averaging smoothed 버전을 사용할 것을 제안했다.

Conditioned Generation

이미지넷 데이터셋 같은 조건화 정보를 갖는 이미지에 생성 모델을 학습할 때는 클래스 라벨이나 설명 텍스트의 조각에 조건화된 샘플을 생성하는 것이 일반적이다.

Classifier Guided Diffusion

클래스 정보를 diffusion 프로세스에 명시적으로 통합하기 위해 Dhariwal & Nichol(2021)은 noisy 이미지 xt\mathbf{x}_t에 분류기 fϕ(y∣xt,t)f_\phi(y \vert \mathbf{x}_t, t)를 학습하고 gradient ∇xlog⁡fϕ(y∣xt)\nabla_\mathbf{x} \log f_\phi(y \vert \mathbf{x}_t)를 사용하여 노이즈 예측을 변경하여 조건 정보 yy (예: 목표 클래스 라벨)로 diffusion 샘플링 프로세스를 가이드한다.
∇xtlog⁡q(xt)=−11−αˉtϵθ(xt,t)\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) = - \frac{1}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)과 결합 분포 q(xt,y)q(\mathbf{x}_t, y)에 대한 score 함수를 다음과 같이 작성할 수 있다는 것을 떠올려라.
∇xtlog⁡q(xt,y)=∇xtlog⁡q(xt)+∇xtlog⁡q(y∣xt)≈−11−αˉtϵθ(xt,t)+∇xtlog⁡fϕ(y∣xt)=−11−αˉt(ϵθ(xt,t)−1−αˉt∇xtlog⁡fϕ(y∣xt))\begin{aligned}\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t, y)&= \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) + \nabla_{\mathbf{x}_t} \log q(y \vert \mathbf{x}_t) \\&\approx - \frac{1}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) + \nabla_{\mathbf{x}_t} \log f_\phi(y \vert \mathbf{x}_t) \\&= - \frac{1}{\sqrt{1 - \bar{\alpha}_t}} (\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) - \sqrt{1 - \bar{\alpha}_t} \nabla_{\mathbf{x}_t} \log f_\phi(y \vert \mathbf{x}_t))\end{aligned}
따라서 새로운 classifier-guided 예측기 ϵˉθ\bar{\boldsymbol{\epsilon}}_\theta 는 다음과 같은 형식을 취한다.
ϵˉθ(xt,t)=ϵθ(xt,t)−1−αˉt∇xtlog⁡fϕ(y∣xt)\bar{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) = \boldsymbol{\epsilon}_\theta(x_t, t) - \sqrt{1 - \bar{\alpha}_t} \nabla_{\mathbf{x}_t} \log f_\phi(y \vert \mathbf{x}_t)
classifier guidance의 강도를 제어하기 위해 델타 부분에 가중치 ww 를 추가할 수 있다.
ϵˉθ(xt,t)=ϵθ(xt,t)−1−αˉt  w∇xtlog⁡fϕ(y∣xt)\bar{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) = \boldsymbol{\epsilon}_\theta(x_t, t) - \sqrt{1 - \bar{\alpha}_t} \; w \nabla_{\mathbf{x}_t} \log f_\phi(y \vert \mathbf{x}_t)
결과 ablated diffusion model(ADM)과 추가로 classifier guidance(ADM-G)를 갖는 버전은 최신 성능 생성 모델(예: BigGAN) 보다 나은 결과를 달성했다.
추가적으로 U-Net 아키텍쳐에 대해 일부 수정을 통해 Dhariwal & Nichol(2021)은 diffusion model을 사용하는 GAN보다 나은 성능을 보였다. 아키텍쳐 수정에는 더 큰 모델 깊이와 너비, 더 많은 attention head, multi-resolution attention, up/down sampling에 대한 BigGAN residual block, 1/21/\sqrt{2}에 의한 residual connection rescale과 adaptive group normalization(AdaGN)이 포함된다.

Classifier-Free Guidance

독립적인 classifier fϕf_\phi 없이도 conditional과 unconditional diffusion 모델에서 score를 통합하여 조건부 diffusion step을 실행하는 것이 가능하다. (Ho & Salimans, 2021). score 추정기 ϵθ(xt,t)\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)을 통해 파라미터화 된 unconditional denoising diffusion 모델 pθ(x)p_\theta(\mathbf{x})와 ϵθ(xt,t,y)\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y)를 통해 파라미터화 된 conditional 모델 pθ(x∣y)p_\theta(\mathbf{x} \vert y)를 예로 들어보자. 이 두 모델은 단일 신경망을 통해 학습될 수 있다. 정확히 말하면 conditional diffusion 모델 pθ(x∣y)p_\theta(\mathbf{x} \vert y)는 paired 데이터 (x,y)(\mathbf{x}, y)에 대해 학습된다. 여기서 조건 정보 yy는 주기적으로 랜덤으로 폐기되어 모델이 unconditionally 이미지를 생성하는 방법도 알게 한다. 즉 ϵθ(xt,t)=ϵθ(xt,t,y=∅)\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) = \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y=\varnothing)
암시적 분류기의 gradient는 conditional과 unconditional score 추정기를 사용하여 표현할 수 있다. classifier-guided 수정된 score에 연결하면 score는 별도의 classifier에 대한 의존성을 포함하지 않는다.
∇xtlog⁡p(y∣xt)=∇xtlog⁡p(xt∣y)−∇xtlog⁡p(xt)=−11−αˉt(ϵθ(xt,t,y)−ϵθ(xt,t))ϵˉθ(xt,t,y)=ϵθ(xt,t,y)−1−αˉt  w∇xtlog⁡p(y∣xt)=ϵθ(xt,t,y)+w(ϵθ(xt,t,y)−ϵθ(xt,t))=(w+1)ϵθ(xt,t,y)−wϵθ(xt,t)\begin{aligned}\nabla_{\mathbf{x}_t} \log p(y \vert \mathbf{x}_t)&= \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t \vert y) - \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t) \\&= - \frac{1}{\sqrt{1 - \bar{\alpha}_t}}\Big( \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big) \\\bar{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t, y)&= \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) - \sqrt{1 - \bar{\alpha}_t} \; w \nabla_{\mathbf{x}_t} \log p(y \vert \mathbf{x}_t) \\&= \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) + w \big(\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \big) \\&= (w+1) \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, y) - w \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\end{aligned}
그들의 실험에 따르면 classifier-free guidance가 FID(합성과 생성 이미지 사이의 구별)와 IS(품질과 다양성) 사이의 좋은 균형을 달성함하는 것으로 나타났다.
guided diffusion model인 GLIDE(Nichol, Dhariwal & Ramesh 외. 2022)에서 CLIP guidance와 classifier-free guidance에 대한 두 가지 guiding 전략을 모두 살펴본 결과 후자가 더 선호된다는 것을 발견했매

Speed up Diffusion Models

TT가 1에서 수천 단계에 이를 수 있기 때문에 reverse diffusion 프로세스의 Markov 체인에 의해 DDPM에서 샘플을 생성하는 것은 매우 느리다. 송 등의(2020) 한 데이터 포인트: 예컨대 DDPM에서 32x32 크기의 이미지 5만개를 샘플링하는데는 약 20시간이 걸리지만, Nvidia 2080 Ti GPU에서 GAN은 1분도 걸리지 않는다.

Fewer Sampling Steps & Distillation

한 가지 단순한 방법은 프로세스를 TT에서 SS step으로 줄이기 위해 [T/S][T/S] 단계마다 샘플링 업데이트를 취하는 strided 샘플링 스케쥴(Nichol & Dhariwal, 2021)을 수행하는 것이다. 생성을 위한 새로운 샘플링 스케쥴은 {τ1<τ2<⋯<τS}\{\tau_1 < \tau_2 < \dots <\tau_S \}이다. 여기서 τ1<τ2<⋯<τS∈[1,T]\tau_1 < \tau_2 < \dots <\tau_S \in [1, T]이고 S<TS < T
또 다른 접근에 대해 nice property를 따라 원하는 표준 편차 σt\sigma_t에 의해 파라미터화 되도록 qσ(xt−1∣xt,x0)q_\sigma(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)를 재작성해 보겠다.
xt−1=αˉt−1x0+1−αˉt−1ϵt−1=αˉt−1x0+1−αˉt−1−σt2ϵt+σtϵ=αˉt−1(xt−1−αˉtϵθ(t)(xt)αˉt)+1−αˉt−1−σt2ϵθ(t)(xt)+σtϵqσ(xt−1∣xt,x0)=N(xt−1;αˉt−1(xt−1−αˉtϵθ(t)(xt)αˉt)+1−αˉt−1−σt2ϵθ(t)(xt),σt2I)\begin{aligned} \mathbf{x}_{t-1} &= \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1}}\boldsymbol{\epsilon}_{t-1} & \\ &= \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \boldsymbol{\epsilon}_t + \sigma_t\boldsymbol{\epsilon} & \\ &= \sqrt{\bar{\alpha}_{t-1}} \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \epsilon^{(t)}_\theta(\mathbf{x}_t) + \sigma_t\boldsymbol{\epsilon} \\ q_\sigma(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_{t-1}; \sqrt{\bar{\alpha}_{t-1}} \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \epsilon^{(t)}_\theta(\mathbf{x}_t), \sigma_t^2 \mathbf{I}) \end{aligned}
여기서 모델 ϵθ(t)(.)\epsilon^{(t)}_\theta(.)는 xt\mathbf{x}_t에서 ϵt\epsilon_t를 예측한다.
q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\boldsymbol{\mu}}(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t \mathbf{I})을 떠올려라. 따라서 다음이 성립한다.
β~t=σt2=1−αˉt−11−αˉt⋅βt\tilde{\beta}_t = \sigma_t^2 = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t
샘플링 확률성을 제어하기 위한 η∈R+\eta \in \mathbb{R}^+를 하이퍼파라미터로 조정할 수 있도록 σt2=η⋅β~t\sigma_t^2 = \eta \cdot \tilde{\beta}_t라 한다. η=0\eta = 0인 특수한 경우에 샘플링 프로세스를 결정론적이 된다. 이런 모델을 denoising diffusion implicit model(DDIM; Song et al, 2020)이라 한다. DDIM은 동일한 marginal noise 분포를 갖지만 노이즈를 원본 데이터 샘플에 결정론적으로 다시 매핑한다.
생성하는 동안 전체 체인 t=1,..,Tt=1,..,T를 따르는 것이 아니라 단계의 부분 집합을 따른다. s<ts <t를 이 가속화된 궤적에서 2단계로 표기하자. DDIM 업데이트 단계는 다음과 같다.
qσ,τ(xτi−1∣xτt,x0)=N(xτi−1;αˉt−1x0+1−αˉt−1−σt2xτi−αˉtx01−αˉt,σt2I)q_{\sigma, \tau}(\mathbf{x}_{\tau_{i-1}} \vert \mathbf{x}_{\tau_t}, \mathbf{x}_0)= \mathcal{N}(\mathbf{x}_{\tau_{i-1}}; \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \frac{\mathbf{x}_{\tau_i} - \sqrt{\bar{\alpha}_t}\mathbf{x}_0}{\sqrt{1 - \bar{\alpha}_t}}, \sigma_t^2 \mathbf{I})
T=1000T=1000 diffusion step을 사용하여 모델을 학습한 실험에서, SS가 작을 때 DDIM(η=0\eta = 0)이 가장 높은 품질의 샘플을 생성할 수 있지만 DDPM(η=1\eta = 1)의 성능은 더 나쁜 것을 관찰했다. full reverse Markov diffusion step(S=T=1000S = T = 1000)을 수행할 수 있을 때 DDPM이 더 나은 수행을 했다. DDIM을 사용하면 임의의 수의 forward step까지 diffusion 모델을 수행할 수 있지만 생성 프로세스의 step의 부분집합에서만 샘플링할 수 있다.
DDPM과 비교하여 DDIM은 다음이 가능하다.
1.
훨씬 적은 수의 단계로 더 높은 품질의 샘플을 생성할 수 있다.
2.
생성 프로세스가 결정론적이기 때문에 '일관성' 속성을 가지며, 이는 동일한 잠재 변수에 조건화 된 여러 샘플이 유사한 상위 수준의 특징을 가져야 함을 의미한다.
3.
일관성 때문에 DDIM은 잠재 변수에서 semantically 의미 있는 보간을 수행할 수 있다.
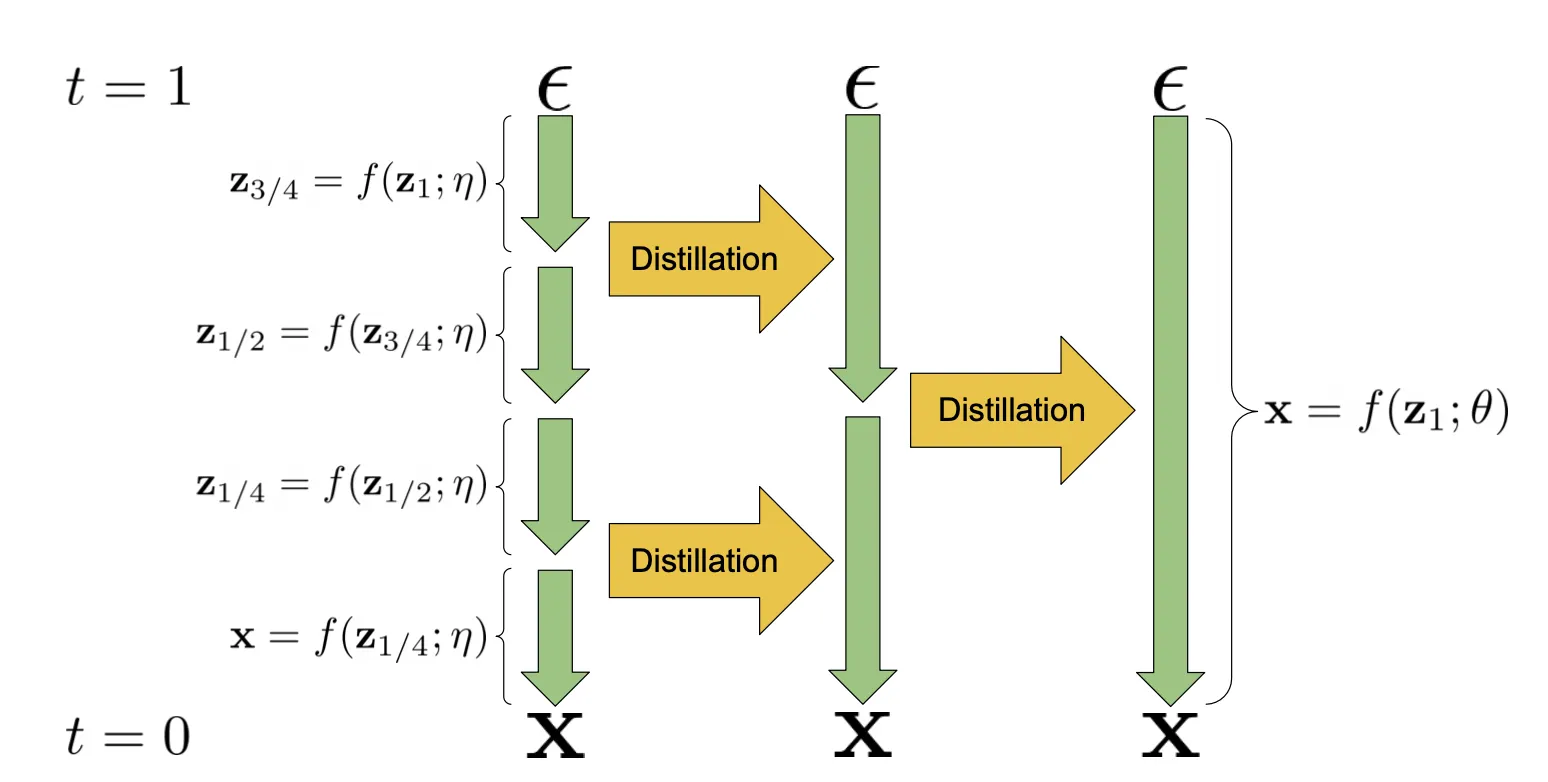
Progressive Distillation (Salimans & Ho, 2022)는 학습된 결정론적 샘플러를 절반 샘플링 단계의 새로운 모델로 distilling(증류) 하는 방법이다. 학생 모델은 교사 모델로 초기화되고 원본 샘플 x0\bold{x}_0을 denoise target으로 사용하는 대신 하나의 학생 DDIM step이 2개의 교사 단계와 일치하는 target을 향해 denoise 한다. 매 progressive distillation 반복에서 샘플링 step을 절반으로 줄일 수 있다.
Consistency Model (Song et al. 2023)은 diffusion 샘플링 궤적에서 임의의 중간 noisy 데이터 포인트 xt,t>0\bold{x}_t, t> 0을 원본 x0\bold{x}_0에 직접 매핑하는 방법을 학습한다. 동일한 궤적에 있는 데이터 포인트가 모두 동일한 원점에 매핑되는 self-consistency라는 속성 때문에 consistency model이라 불린다.
궤적 {xt∣t∈[ϵ,T]}\{\mathbf{x}_t \vert t \in [\epsilon, T]\}이 주어지면 consistency 함수 ff는 f:(xt,t)↦xϵf: (\mathbf{x}_t, t) \mapsto \mathbf{x}_\epsilon로 정의되고 등식 f(xt,t)=f(xt’,t’)=xϵf(\mathbf{x}_t, t) = f(\mathbf{x}_{t’}, t’) = \mathbf{x}_\epsilon는 모든 t,t’∈[ϵ,T]t, t’ \in [\epsilon, T]에 대해 참이다. t=ϵt=\epsilon이면 ff는 항등 함수이다. 모델은 다음과 같이 파라미터화 될 수 있다. 여기서 cskip(t)c_\text{skip}(t)와 cout(t)c_\text{out}(t) 함수는 cskip(ϵ)=1,cout(ϵ)=0c_\text{skip}(\epsilon) = 1, c_\text{out}(\epsilon) = 0인 방법으로 설계된다.
fθ(x,t)=cskip(t)x+cout(t)Fθ(x,t)f_\theta(\mathbf{x}, t) = c_\text{skip}(t)\mathbf{x} + c_\text{out}(t) F_\theta(\mathbf{x}, t)
consistency 모델은 multi-step 샘플링 프로세스를 따라 더 나은 품질을 위해 trading computation의 유연성을 유지하면서 단일 step으로 샘플을 생성할 수 있다.
그 논문은 consistency 모델을 학습하는 2가지 방법을 소개했다.
1.
Consistency Distillation (CD)
동일한 궤적에서 생성된 쌍에 대한 모델 출력 사이의 차이를 최소화하여 diffusion 모델을 consistency 모델로 distill 한다. 이를 통해 훨씬 더 저렴한 샘플링 평가가 가능하다. consistency distillation loss는 다음과 같다.
 LCDN(θ,θ−;ϕ)=E [λ(tn)d(fθ(xtn+1,tn+1),fθ−(x^tnϕ,tn)] x^tnϕ=xtn+1−(tn−tn+1)Φ(xtn+1,tn+1;ϕ) \begin{aligned} \mathcal{L}^N_\text{CD} (\theta, \theta^-; \phi) &= \mathbb{E} [\lambda(t_n)d(f_\theta(\mathbf{x}_{t_{n+1}}, t_{n+1}), f_{\theta^-}(\hat{\mathbf{x}}^\phi_{t_n}, t_n)] \\ \hat{\mathbf{x}}^\phi_{t_n} &= \mathbf{x}_{t_{n+1}} - (t_n - t_{n+1}) \Phi(\mathbf{x}_{t_{n+1}}, t_{n+1}; \phi) \end{aligned}
여기서
•
Φ(.;ϕ)\Phi(.;\phi)는 one-step ODE solver의 업데이트 함수이다.
•
n∼U[1,N−1]n \sim \mathcal{U}[1, N-1]는 1,…,N−11, \dots, N-1에 대한 균등 분포를 갖는다.
•
네트워크 파라미터 θ−\theta^-는 학습을 매우 안정 시키는 θ\theta의 EMA 버전이다.(DQN 또는 momentum contrastive learning 같은)
•
d(.,.)d(.,.)는 ℓ2\ell_2, ℓ1\ell_1 또는 LPIPS(learned perceptual image patch similarity) 거리 같이 ∀x,y:d(x,y)≤0\forall \mathbf{x}, \mathbf{y}: d(\mathbf{x}, \mathbf{y}) \leq 0이고 d(x,y)=0d(\mathbf{x}, \mathbf{y}) = 0이면 x=y\mathbf{x} = \mathbf{y}이고 iff를 만족하는 positive distance metric 함수이다.
•
λ(.)∈R+\lambda(.) \in \mathbb{R}^+는 positive weighting 함수이고 논문에서는 λ(tn)=1\lambda(t_n)=1을 설정했다.
2.
Consistency Training (CT)
다른 옵션은 consistency 모델을 독립적으로 훈련하는 것이다. CD에서는 pre-trained score model sϕ(x,t)s_\phi(\mathbf{x}, t)이 ground truth score ∇log⁡pt(x)\nabla\log p_t(\mathbf{x})를 근사하기 위해 사용되지만 CT에서는 이 score 함수를 추정하는 방법이 필요하고 ∇log⁡pt(x)\nabla\log p_t(\mathbf{x})의 비편향 추정기가 −xt−xt2-\frac{\mathbf{x}_t - \mathbf{x}}{t^2}로 존재한다는 것이 밝혀졌다. CT loss는 다음처럼 정의된다.
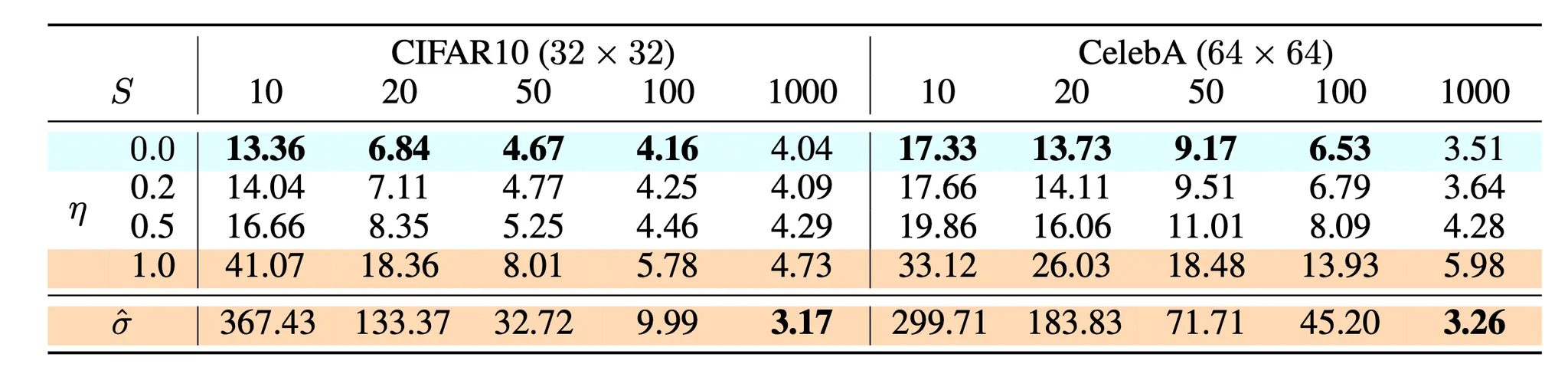
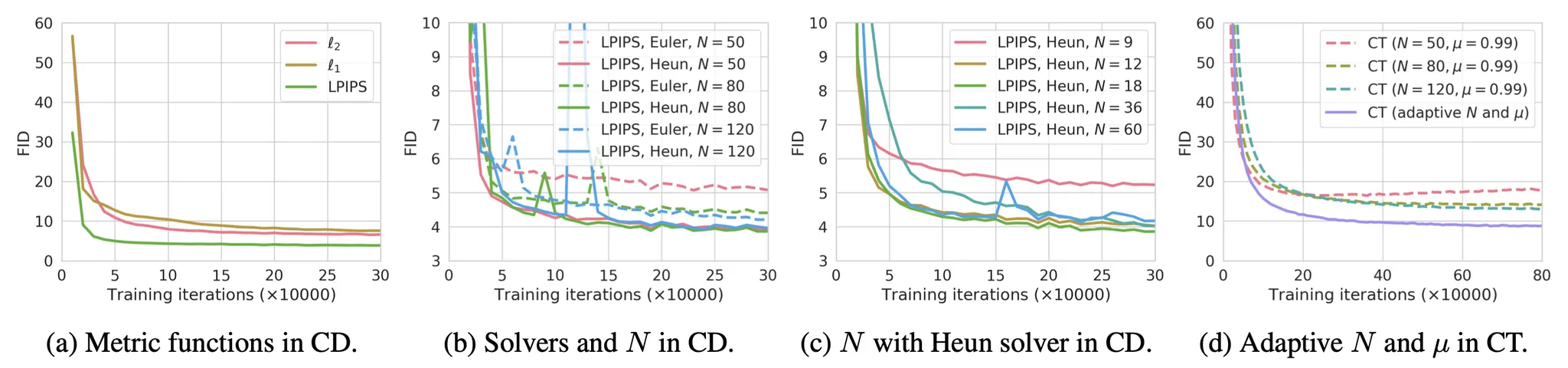
LCTN(θ,θ−;ϕ)=E[λ(tn)d(fθ(x+tn+1z,  tn+1),fθ−(x+tnz,  tn)] where z∈N(0,I)\mathcal{L}^N_\text{CT} (\theta, \theta^-; \phi) = \mathbb{E}[\lambda(t_n)d(f_\theta(\mathbf{x} + t_{n+1} \mathbf{z},\;t_{n+1}), f_{\theta^-}(\mathbf{x} + t_n \mathbf{z},\;t_n)]\\\text{ where }\mathbf{z} \in \mathcal{N}(\mathbf{0}, \mathbf{I})
그 논문의 실험에 따르면 그들은 다음을 발견햇다.
•
고차 ODE solver가 동일한 NN에서 더 작은 추정 에러를 갖기 때문에 Heun ODE solver가 Euler’s first-order solver 보다 잘 작동한다.
•
거리 메트릭 함수 d(.)d(.)의 다양한 옵션 사이에서 LPIPS 메트릭은 ℓ1\ell_1과 ℓ2\ell_2 거리보다 더 잘 작동했다.
•
NN이 작을수록 수렴이 빨라지지만 샘플은 나쁘고, NN이 클수록 수렴은 느려지지만 수렴시 샘플은 더 좋아진다.

Latent Variable Space

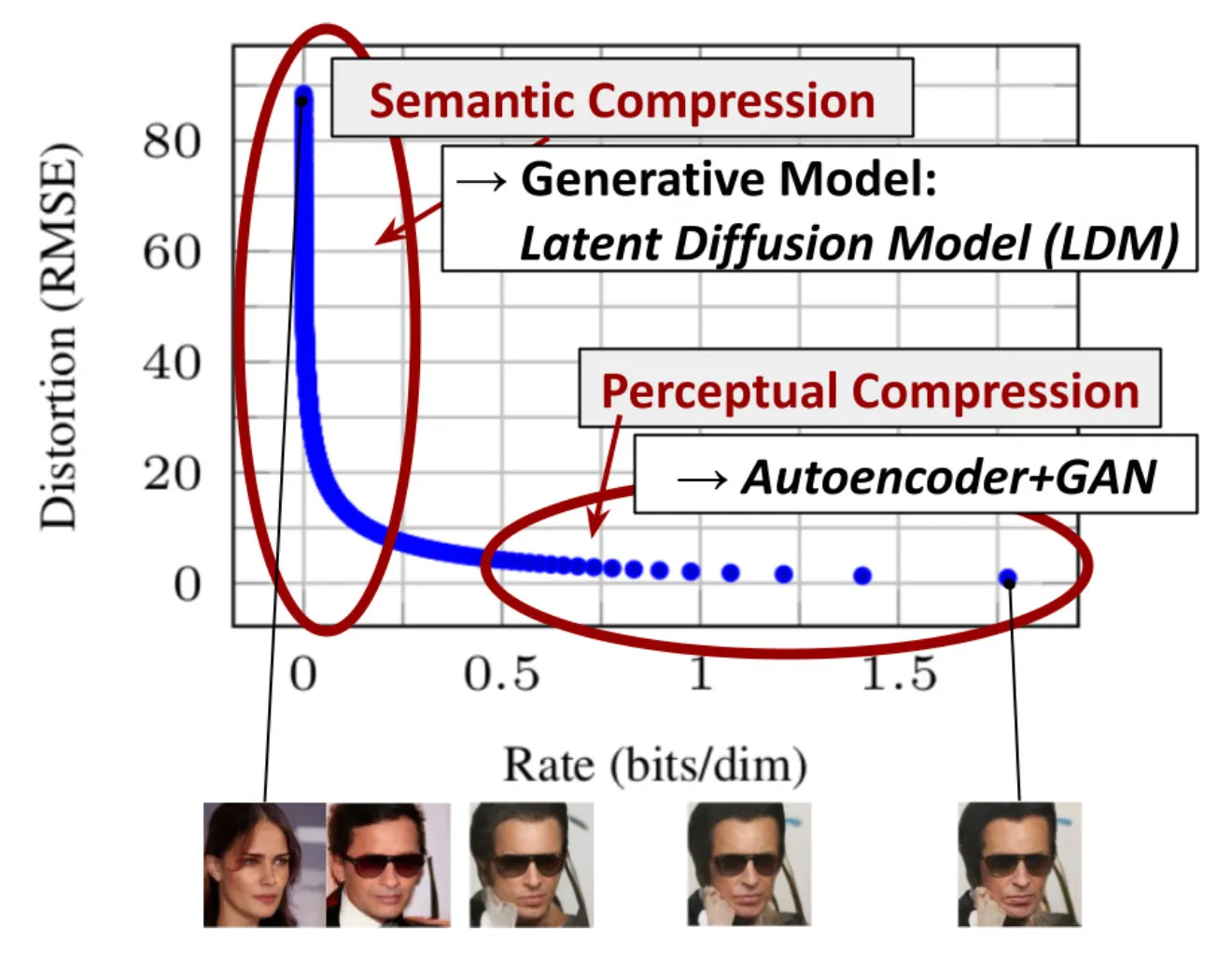
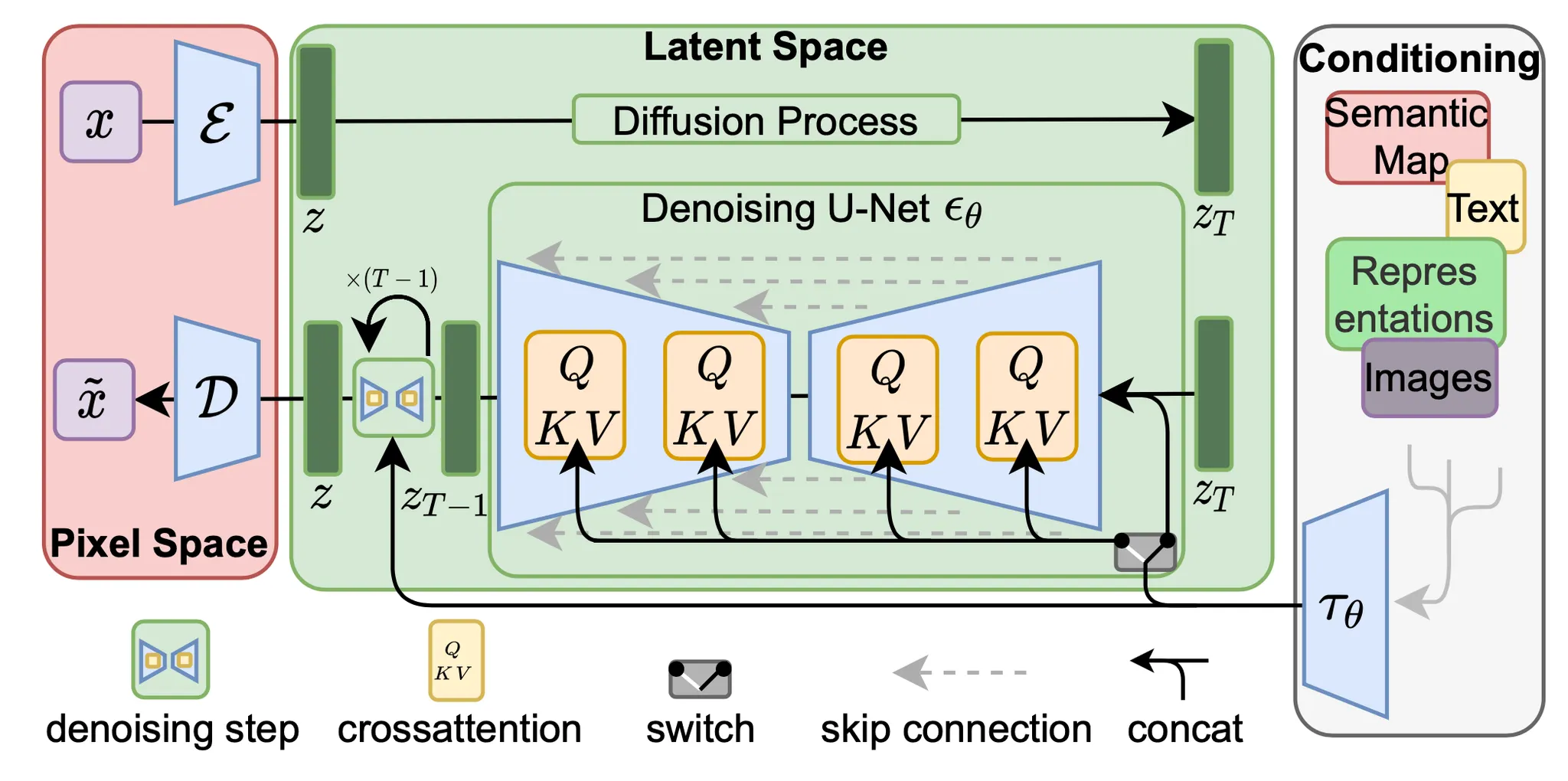
Latent Diffusion odel(LDM; Rombach & Blattmann 등, 2022)은 픽셀 공간 대신 latent 공간에서 diffusion 프로세스를 실행하여 훈련 비용은 낮추고 추론 속도는 더 빠르게 한다. 이는 이미지의 대부분의 비트가 지각적 디테일에 기여하고 공격적인 압축 후에도 의미 및 개념적 구성이 여전히 남아 있다는 관찰에 기반합니다. LDM은 먼저 autoencoder로 픽셀 수준의 중복성을 제거한 다음 학습된 latent에 대한 diffusion 프로세스를 통해 의미적 개념을 조작/생성하는 방식으로 지각적 압축과 의미적 압축을 생성 모델링 학습으로 느슨하게 분해합니다.
지각적 압축 프로세스는 autoencoder 모델에 의존합니다. 인코더 E\mathcal{E}는 입력 이미지 x∈RH×W×3\mathbf{x} \in \mathbb{R}^{H \times W \times 3}를 더 작은 2D latent 벡터 z=E(x)∈Rh×w×c\mathbf{z} = \mathcal{E}(\mathbf{x}) \in \mathbb{R}^{h \times w \times c}로 압축하는 데 사용되며, 여기서 다운샘플링 비율은 f=H/h=W/w=2m,m∈Nf=H/h=W/w=2^m, m \in \mathbb{N}입니다. 그 다음 디코더 D\mathcal{D}는 latent 벡터에서 이미지를 재구성합니다. x~=D(z)\tilde{\mathbf{x}} = \mathcal{D}(\mathbf{z}). 해당 논문에서 autoencoder 학습에서 두 가지 유형의 정규화를 통해 latent 공간에서 임의의 높은 분산을 피할 수 있는 방법을 살펴봤습니다.
•
KL-reg: VAE와 유사하게 학습된 latent에 대해 표준 정규 분포 방향으로 작은 KL 페널티
•
VQ-reg: VQVAE와 유사하게 디코더 내에서 벡터 양자화 계층을 사용하지만 양자화 계층은 디코더에 흡수 됨
diffusion 및 denoising 프로세스는 잠재 벡터 z\bold{z}에서 발생합니다. denoising 모델은 시간-조건화된 U-Net으로 이미지 생성을 위한 유연한 조건화 정보를 다루기 위해 cross-attention 메커니즘을 사용하여 강화된다. (예, 클래스 라벨, semantic map, 이미지의 blurred 변종). 이 디자인은 cross-attention 메커니즘을 통해 서로 다른 modality의 표현을 모델에 융합하는 것과 같다. 각 유형의 조건화된 정보는 도메인별 인코더 τθ\tau_\theta와 짝을 이루어 cross-attention 컴포넌트로 매핑될 수 있는 중간 표현에 조건화된 입력 yy을 투영한다. τθ(y)∈RM×dτ\tau_\theta(y) \in \mathbb{R}^{M \times d_\tau}
Attention(Q,K,V)=softmax(QK⊤d)⋅Vwhere Q=WQ(i)⋅φi(zi),  K=WK(i)⋅τθ(y),  V=WV(i)⋅τθ(y)and WQ(i)∈Rd×dϵi,  WK(i),WV(i)∈Rd×dτ,  φi(zi)∈RN×dϵi,  τθ(y)∈RM×dτ\begin{aligned}&\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}\Big(\frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{d}}\Big) \cdot \mathbf{V} \\&\text{where }\mathbf{Q} = \mathbf{W}^{(i)}_Q \cdot \varphi_i(\mathbf{z}_i),\;\mathbf{K} = \mathbf{W}^{(i)}_K \cdot \tau_\theta(y),\;\mathbf{V} = \mathbf{W}^{(i)}_V \cdot \tau_\theta(y) \\&\text{and }\mathbf{W}^{(i)}_Q \in \mathbb{R}^{d \times d^i_\epsilon},\;\mathbf{W}^{(i)}_K, \mathbf{W}^{(i)}_V \in \mathbb{R}^{d \times d_\tau},\;\varphi_i(\mathbf{z}_i) \in \mathbb{R}^{N \times d^i_\epsilon},\;\tau_\theta(y) \in \mathbb{R}^{M \times d_\tau}\end{aligned}

Scale up Generation Resolution and Quality

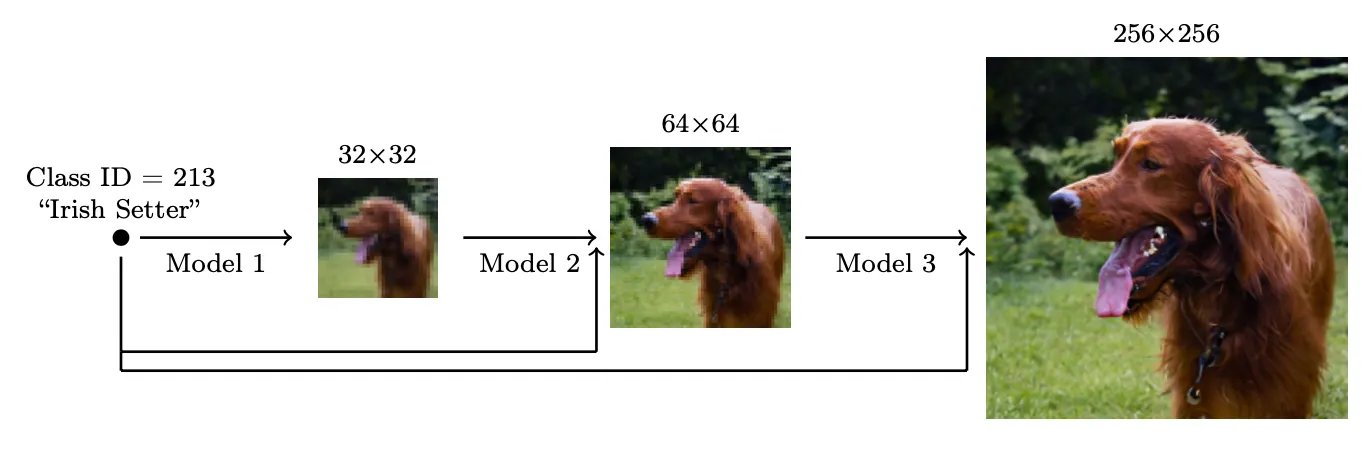
높은 해상도에서 높은 품질의 이미지를 생성하기 위해 Ho et al. (2021)은 해상도를 증가시킬 때 여러 diffusion 모델의 pipeline을 사용할 것을 제안했다. pipeline 모델 사이의 Noise Conditioning Augmentation(NCA)가 최종 이미지 품질에 핵심이다. NCA는 각 super-resolution 모델 pθ(x∣z)p_\theta(\mathbf{x} \vert \mathbf{z})의 conditioning 입력 z\mathbf{z}에 강력한 데이터 augmentation을 적용하는 것을 말한다. conditioning 노이즈는 pipeline 설정에서 복합 에러를 줄이는데 도움이 된다. U-net은 고해상도 이미지 생성을 위한 diffusion 모델링에서 모델 아키텍쳐의 일반적인 선택이다.
그들은 저해상도에서는 가우시안 노이즈를 적용하고 고해상도에서는 가우시안 블러를 적용하는 것이 가장 효과적인 노이즈라는 것을 발견했다. 또한 학습 프로세스에 작은 수정이 필요한 conditioning augmentation의 2가지 형식을 살펴보았다. conditioning 노이즈는 학습에만 적용되고 추론에는 적용되지 않는다는 것에 유의하라.
•
Truncated conditioning augmentation은 저해상도에 대해 step t>0t > 0에서 diffusion 프로세스를 조기에 중지한다.
•
Non-truncated conditioning augmentation은 step 0까지 전체 저해상도 reverse 프로세스를 실행하지만 zt∼q(xt∣x0)\mathbf{z}_t \sim q(\mathbf{x}_t \vert \mathbf{x}_0)만큼 오염 시키고, 그 다음 오염된 zt\mathbf{z}_t를 super resolution 모델에 공급한다.
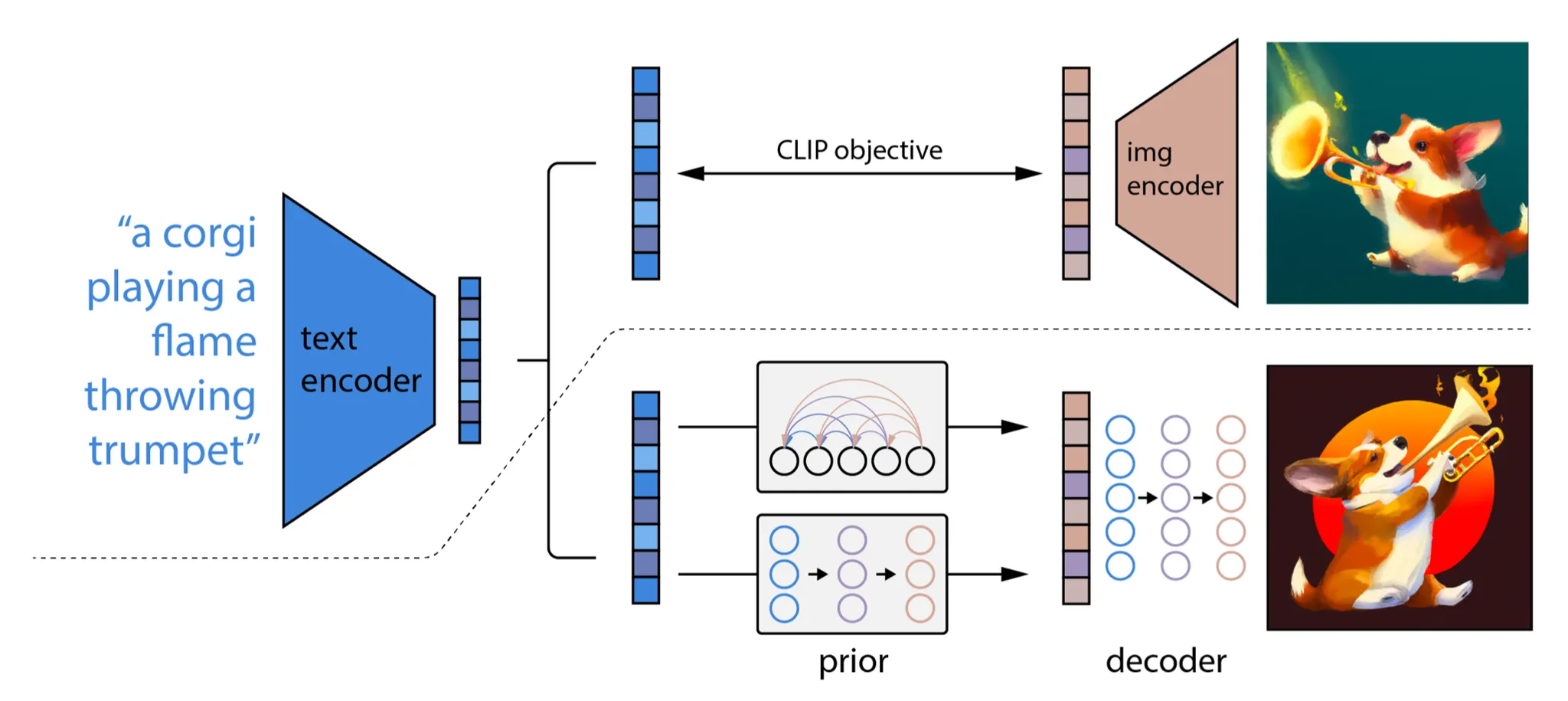
2-stage diffusion model unCLIP(Ramesh, 2022)은 고 품질에서 text-guided 이미지를 생성하도록 CLIP 텍스트 인코더를 많이 활용했다. pretrained CLIP 모델 cc와 diffusion 모델에 대한 쌍별 학습 데이터가 주어지면 (x,y)(\bold{x}, y) (여기서 x\bold{x}는 이미지이고 yy는 해당 캡션) CLIP text와 이미지 embedding을 각각 계산할 수 있다. ct(y)\mathbf{c}^t(y)와 ci(x)\mathbf{c}^i(\mathbf{x}). unCLIP은 병렬로 2가지 모델을 학습한다.
•
prior model P(ci∣y)P(\mathbf{c}^i \vert y): 텍스트 yy가 주어질 때 출력 CLIP 이미지 embedding ci\mathbf{c}^i
•
디코더 P(x∣ci,[y])P(\mathbf{x} \vert \mathbf{c}^i, [y]): CLIP 이미지 embedding ci\mathbf{c}^i와 optional 로 원본 텍스트 yy가 주어질 때 이미지 x\mathbf{x}를 생성.
이 두 모델은 조건부 생성을 가능하게 한다. 왜냐하면
P(x∣y)=P(x,ci∣y)⏟ci is deterministic given x=P(x∣ci,y)P(ci∣y)\underbrace{P(\mathbf{x} \vert y) = P(\mathbf{x}, \mathbf{c}^i \vert y)}_{\mathbf{c}^i\text{ is deterministic given }\mathbf{x}} = P(\mathbf{x} \vert \mathbf{c}^i, y)P(\mathbf{c}^i \vert y)
unCLIP은 2단계 이미지 생성 프로세스를 따른다:
1.
텍스트 yy가 주어지면 CLIP 모델은 우선 텍스트 임베딩 ct(y)\mathbf{c}^t(y)을 생성하도록 사용된다. CLIP latent 공간을 사용하여 텍스트를 통해 zero-shot image manipulation이 가능하다.
2.
diffusion 또는 autoregressive prior P(ci∣y)P(\mathbf{c}^i \vert y)가 이 CLIP 텍스트 임베딩을 처리하여 이미지 prior를 구성한 다음 diffusion decoder P(x∣ci,[y])P(\mathbf{x} \vert \mathbf{c}^i, [y])가 prior에 조건화된 이미지를 생성한다. 이 디코더는 또한 스타일과 semantics를 보존하며 이미지 입력에 조건화된 이미지 변종을 생성할 수도 있다.
CLIP 대신 Imagen(Saharia, 2022)는 pre-trained 대형 LM(예: frozen T5-XXL text encoder)을 사용하여 이미지 생성에 대한 텍스트를 인코드 했다. 더 큰 모델 크기는 더 나은 이미지 품질과 text-image alignment를 이끄는 일반적인 경향이 존재한다. 그들은 T5-XXL과 CLIP text 인코더가 MS-COCO에 대해 유사한 성능을 달성했지만 인간 평가자는 DrawBench(11개 카테고리를 커버하는 프롬프트의 컬렉션)에 대해 T5-XXL을 더 선호 했다.
classifier-free guidance를 적용할 때, ww를 증가시키면 더 나은 image-text alignment를 이끌지만 이미지 fidelity(충실도)는 낮아진다. 그들은 이것이 train-test 미스매치 때문이라는 것을 발견했다. 이것은 다시 말해 학습 데이터 x\bold{x}가 [−1,1][-1,1] 범위 내에 있기 때문에 테스트 데이터도 그래야 한다. 두 thresholding 전략이 유도되었다.
•
static thresholding: x\bold{x} 예측을 [−1,1][-1,1]로 clip 한다.
•
dynamic thresholding: 각 샘플링 단계에서 ss를 특정한 백분위수 절대 픽셀 값으로 계산. s>1s > 1이면 예측을 [−s,s][-s, s]로 clip하고 ss로 나눈다.
Imagen은 U-net에서 여러 설계를 수정하고 efficient U-Net을 만들었다.
•
낮은 해상도에 더 많은 residual lock을 추가하여 모델 파라미터를 고해상도 블록에서 저해상도로 이동
•
skip connection을 1/21/\sqrt{2}로 확장
•
forward pass의 속도를 개선하는 측면에서 downsampling(convolution 전에 이동)과 upsampling(convolution 후에 이동) 연산의 순서를 반전.
그들은 noise conditioning 증강, dynamic thresholding과 efficient U-Net이 이미지 품질에 더 중요하지만 텍스트 인코더 크기를 scaling하는 것이 U-Net 크기 보다 중요하다는 것을 발견했다.

Model Architecture

일반적으로 diffusion 모델에 대한 2가지 backbone 아키텍쳐 선택이 존재한다. U-Net과 Transformer이다.
U-Net(Ronneberger, 2015)는 downsampling stack과 upsampling stack의 구성이다.
•
Downsampling: 각 단계는 2개의 3x3 convolution(unpadded convolution)을 반복적으로 적용한 다음, 각각 ReLU, stride 2의 2x2 max pooling을 적용하는 것으로 구성된다. 각 downsampling 단계마다 feature channel은 2배가 된다.
•
Upsampling: 각 단계는 feature map의 upsampling과 2x2 convolution으로 구성되며 각각 feature channel의 수를 절반으로 줄인다.
•
Shortcuts: Shortcut connection은 downsampling stack의 해당 레이어와 연결되며 upsampling 프로세스에 필수적인 고해상도 feature를 제공한다.
Canny edges, Hough lines, user scribbles, human post skeletons, segmentation maps, depths and normals 같은 구성 정보에 대한 추가 이미지를 조건으로 이미지를 생성할 수 있도록 ControlNet(Zhang 등, 2023)은 U-Net의 각 인코더 레이어에 원본 모델 가중치의 학습 가능한 복사본인 ‘샌드위치’된 zero convolution layer를 추가하여 아키텍쳐의 변화를 도입한다. 정확하게 신경망 블록 Fθ(.)\mathcal{F}_\theta(.)가 주어지면 ControlNet은 다음을 수행한다.
1.
우선 원래 블록의 원래 파라미터 θ\theta을 freeze 한다.
2.
학습 가능한 파라미터 θ\theta와 추가적인 conditioning 벡터 c\mathbf{c}를 사용하여 복사본으로 복제한다.
3.
이 두 블록을 연결하기 위해 Zθz1(.;.)\mathcal{Z}_{\theta_{z1}}(.;.)와 Zθz2(.;.)\mathcal{Z}_{\theta_{z2}}(.;.)로 표기되는 2가지 zero convolution 레이어를 사용한다. 이것은 가중치와 bias 모두 0으로 초기화된 1x1 conv layer이다. Zero convolution은 초기 학습 단계에서 gradient의 랜덤 노이즈를 제거하여 이 back-bone을 보호한다.
4.
최종 출력은 다음과 같다. yc=Fθ(x)+Zθz2(Fθc(x+Zθz1(c)))\mathbf{y}_c = \mathcal{F}_\theta(\mathbf{x}) + \mathcal{Z}_{\theta_{z2}}(\mathcal{F}_{\theta_c}(\mathbf{x} + \mathcal{Z}_{\theta_{z1}}(\mathbf{c})))
diffusion 모델링을 위한 Diffusion Transformer(DiT, Preebles & Xie, 2023)은 Latent Diffusion Model(LDM)과 동일한 디자인 공간을 사용하여 latent patch에서 작동한다. DiT는 다음 설정을 따른다.
1.
입력 z\bold{z}의 latent 표현을 DiT의 입력으로 취한다.
2.
크기 I×I×CI \times I \times C의 noise latent를 크기 p\bold{p}의 패치로 ‘patchify’ 하고 크기 (I/p)2(I/p)^2의 패치의 시퀀스로 변환한다.
3.
그 다음 이 토큰의 시퀀스를 Transformer 블록에 통과시킨다. 그들은 timestep tt나 클래스 라벨 cc와 같은 contextual 정보에 조건화된 생성을 수행하는 3가지 다른 디자인을 탐험 했다. 3개의 디자인 사이에서 adaLN(Adaptive layer norm)-Zero가 가장 성능이 좋았고 in-context conditioning과 corss-attention block 보다 우수하다. scale과 shift 파라미터 γ\gamma와 β\beta는 tt와 cc의 임베딩 벡터의 합에서 회귀된다. 차원별 스케일링 파라미터 α\alpha 또한 회귀되고 DiT 블록 내의 모든 residual connection에 즉시 prior로 적용된다.
4.
transformer 디코더는 노이즈 예측과 출력 대각 공분산 예측을 출력한다.
트랜스포머 아키텍쳐는 쉽게 확장할 수 있는 것으로 알려져 있다. 이것은 더 많은 컴퓨팅에 따라 성능이 확장되고 실험에 따르면 더 큰 DiT 모델이 더 컴퓨팅 효율적이기 때문에 DiT의 가장 큰 장점 중 하나이다.

Quick Summary

•
장점: 추적 가능성과 유연성은 제너레이티브 모델링에서 상충되는 두 가지 목표이다. 추적 가능한 모델은 분석적으로 평가할 수 있고 가우스 또는 라플라스 등을 통해 저렴하게 데이터를 맞출 수 있지만, 풍부한 데이터 세트의 구조를 쉽게 설명할 수 없다. 유연한 모델은 데이터의 임의의 구조에 맞출 수 있지만, 이러한 모델을 평가, 학습 또는 샘플링하는 데는 일반적으로 비용이 많이 든다. 확산 모델은 분석적으로 추적 가능하고 유연하다.
•
단점: 확산 모델은 샘플을 생성하기 위해 긴 확산 단계의 마르코프 체인에 의존하므로 시간과 컴퓨팅 비용이 상당히 많이 들 수 있다. 프로세스를 훨씬 빠르게 만드는 새로운 방법이 제안되었지만, 샘플링은 여전히 GAN보다 느리다.
Made with