이 블로그 포스트에서 연구자로써 (un)conditional image/audio/video 생성을 위한 Denoising Diffusion Probabilistic Model(DDPM, diffusion models, score-based generative models 또는 단순히 autoencoder라고도 함)을 사용하여 놀라운 결과를 얻을 수 있었던 사례를 살핀다. 이 글을 쓰는 작성 시점에 인기 있는 예제는 OpenAI의 GLIDE와 DALL-E 2, Heidelberg 대학의 Latent Diffusion과 Google Brain의 ImageGen이다.
여기서는 (Ho et al., 2020)의 원본 DDPM 논문을 살펴보고, original TensorFlow 구현에 기반한 Phil Wang의 구현을 바탕으로 PyTorch에서 단계별로 구현을 한다. 생성 모델링에 대한 diffusion의 아이디어는 (Sohl-Dickstein et al., 2015)에 의해 소개되었음에 유의하라. 그러나 (Song et al., 2019) (스탠포드 대학)과 (Ho et al., 2020)(구글 브레인)이 이 접근 방식을 독립적으로 개선하기까지 시간이 걸렸다.
diffusion models에 대해 여러 관점이 존재함에 유의하라. 여기서 이산 시간 관점(latent variable model) 관점을 사용하지만 다른 관점도 확인해 보라.
그럼 시작하자.
우선 필요한 라이브러리들을 설치하고 import 한다.
!pip install -q -U einops datasets matplotlib tqdm
import math
from inspect import isfunction
from functools import partial
%matplotlib inline
import matplotlib.pyplot as plt
from tqdm.auto import tqdm
from einops import rearrange, reduce
from einops.layers.torch import Rearrange
import torch
from torch import nn, einsum
import torch.nn.functional as F
Python
복사
What is a diffusion model?
(denoising) diffusion model은 Normalizing Flows, GANs 또는 VAEs 같은 다른 생성 모델과 비교하면 복잡하지 않다. 이들 모델은 모두 어떤 단순한 분포에서 노이즈를 데이터 샘플로 변환한다. 신경망이 순수 노이즈에서 시작하여 점진적으로 denoise 데이터를 학습하는 경우가 여기에 해당한다.
이미지에 대해 더 상세히 설명하면, 2 단계 프로세스로 구성 된다.
•
고정된 (또는 predefined) forward diffusion process 를 선택하여, 이미지가 순수 노이즈가 될 때까지 점진적으로 가우시안 노이즈를 추가한다.
•
reverse denoising diffusion process 를 학습한다. 여기서 신경망은 순수 노이즈에서 시작하여 실제 이미지에 도달할 때까지 이미지를 점점 denoise 하도록 학습된다.
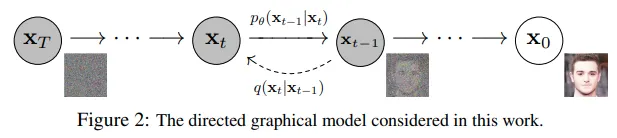
로 인덱싱되는 forward와 reverse process 모두 유한 time steps (DDPM 저자들은 을 사용함) 동안 발생한다. 데이터 분포에서 실제 이미지 를 샘플하는 에서 시작하면(이미지넷에서 고양이 이미지라 가정) forward process 샘플은 각 time step 에서 가우시안 분포에서 약간의 노이즈를 샘플하고 이전 time step의 이미지에 추가한다. 충분히 큰 와 각 time step에서 노이즈를 추가하기 위한 잘 작동하는 스케쥴이 주어지면 점진적 프로세스를 통해 에서 isotropic 가우시안 분포를 얻는다.
In more mathematical form
이것을 더 형식적으로 작성한다. 궁극적으로 우리는 신경망이 최적화하기를 원하는 다루기 용이한 손실 함수가 필요하다.
를 실제 이미지라고 부르는 실제 데이터 분포라고 하자. 이 분포에서 샘플하여 이미지 를 얻을 수 있다. 알려진 분산 스케쥴 을 따라 각 시간 단계 에서 가우시안 노이즈를 추가하는 forward diffusion 프로세스 을 다음과 같이 정의한다.
가우시안 분포가 2가지 파라미터에 의해 정의되는 것을 떠올려라 평균 와 분산 . 기본적으로 시간 단계 에서 각 새로운 (약간 더 노이즈) 이미지는 과 의 conditional 가우시안 분포에서 뽑힌다. 이것은 를 샘플링한 다음 을 설정하여 수행할 수 있다.
는 각 시간 단계 (따라서 아래첨자)에서 일정하지 않다. 실제로 선형, 2차, 코사인 등일 수 있는 소위 ‘분산 스케쥴’을 정의한다. 더 자세히 살펴보겠다. (약간 학습률 스케쥴과 유사하다.)
따라서 에서 시작하여 로 끝난다. 여기서 는 스케쥴을 적절히 설정한 경우 순수 가우시안 노이즈이다.
conditional 분포 을 알면 reverse 프로세스를 실행할 수 있다. 어떤 랜덤 가우시안 노이즈 를 샘플링한 다음 그것을 점진적으로 denoise 하여 최종적으로 실제 데이터 분포 에서 샘플한다.
그러나 을 모른다. 이 조건부 확률을 계산하기 위해 모든 가능한 이미지의 분포를 알아야 하기 때문에 계산이 까다롭다. 따라서 신경망을 활용하여 이 조건부 확률 분포를 근사할 것이다. 이것을 라 부르고 여기서 신경망의 파라미터 는 gradient descent에 의해 업데이트 된다.
이제 backward 프로세스의 (conditional) 확률 분포를 표현하는 신경망이 필요하다. 이 reverse 프로세스가 가우시안이라고 가정하면 모든 가우시안 분포를 2가지 파라미터로 정의할 수 있다는 점을 떠올려라.
•
로 파라미터화 된 평균
•
로 파라미터화 된 분산
따라서 프로세르를 다음과 같이 파라미터화 할 수 있다.
여기서 평균과 분산은 또한 노이즈 레벨 에 의해 조건화 된다.
따라서 신경망은 평균과 분산을 학습/표현 해야 한다. 그러나 DDPM 저자는 분산을 고정하고 신경망이이 조건부 확률 분포의 평균 만 학습(표현)하도록 했다. 논문으로부터
우선 학습되지 않는 시간 종속 상수로 를 설정한다. 실험적으로 와 모두 유사한 결과를 갖는다.
이것은 이후에 Improved diffusion model 논문에서 개선되었다. 여기서 신경망은 평균 뿐만 아니라 이 backward 프로세스의 분산도 학습한다.
따라서 신경망이 이 조건부 확률 분포의 평균만 학습/표현하면 된다고 가정하고 진행한다.
Defining an objective function (by reparametrizing the mean)
backward 프로세스의 평균을 학습하기 위한 목적 함수를 유도하기 위해 저자들은 와 의 결합을 variational auto-encoder(VAE)로 볼 수 있다는 것을 관찰했다. 따라서 variational lower bound(ELBO)을 사용하여 ground truth 데이터 샘플 에 대한 negative log-likelihood를 최소화할 수 있다. (ELBO에 대한 자세한 내용은 VAE 논문 참조) 이 프로세스의 ELBO는 각 시간 단계 에서 손실의 합이라는 것이 밝혀 졌다. . forward 프로세스와 backward 프로세스의 구성에 의해 (을 제외하고) 손실의 각 항은 실제로 평균에 대한 L2 손실로 명시적으로 작성될 수 있는 2개 가우시안 분포 사이의 KL divergence이다.
Sohl-Dickstein et al에 의해 보여진대로 구성된 forward 프로세스 의 직접적인 결과는 을 조건으로 하는 모든 임의의 노이즈 레벨에서 (가우시안의 합은 가우시안이므로) 를 샘플할 수 있다는 것이다. 이것은 매우 편리하다. 를 샘플하기 위해 를 반복적으로 적용할 필요가 없다. 그 이유는 다음과 같다.
여기서 이고 . 이 등식을 ‘nice property’로 참조한다. 이것은 가우시안 노이즈를 샘플링 하고 그것을 적절하게 scale 하고 를 더하면 를 직접 샘플링 할 수 있다는 것을 의미한다. 는 알려진 분산 스케쥴의 함수이므로 미리 계산될 수 있다. 그러면 학습하는 동안 손실 함수 의 무작위 항을 최적화할 수 있다. (즉 학습하는 동안 무작위로 를 샘플링하고 를 최적화할 수 있음)
Ho et al이 보여준 이 속성의 또 다른 좋은 점은 손실을 구성하는 KL 항에서 노이즈 레벨 에 대해 (네트워크 를 통해) 신경망이 추가된 노이즈를 학습 (예측) 하도록 평균을 reparameterize 할 수 있다는 것이다. 이것은 신경망이 (직접적인) 평균 예측기가 아니라 노이즈 예측기가 된다는 것을 의미한다. 평균은 다음처럼 계산될 수 있다.
그러면 최종 목적 함수 는 다음과 같다. (가 주어진 임의의 time step 에 대해)
여기서 은 초기(실제, 오염되지 않은) 이미지이고 고정된 forward 프로세스에 의해 주어지는 직접 노이즈 레벨 샘플을 볼 수 있다. 은 time step 에서 샘플링된 순수 노이즈이고 는 신경망이다. 신경망은 실제와 예측된 가우시안 노이즈 사이의 단순 평균 제곱 에러(MSE)를 사용하여 최적화 된다.
학습 알고리즘은 이제 다음과 같다.
다시 말해
•
실제 알려지지 않은 복잡한 데이터 분포 에서 무작위 샘플 을 취한다.
•
과 사이에서 균등하게 노이즈 레벨 를 샘플링한다. (즉 무작위 time step)
•
가우시안 분포에서 어떤 노이즈를 샘플하고 레벨 에서 이 노이즈로 입력을 오염시킨다. (위에 정의된 nice property를 사용하여)
•
신경망은 오염된 이미지 (즉 알려진 스케쥴 에 기반하여 에 적용된 노이즈)에 기반하여 이 노이즈를 예측하도록 학습된다.
실제로는 stochastic gradient descent를 사용하여 신경망을 최적화 하므로 이 모든 작업은 배치 데이터에서 수행된다.
The neural network
신경망은 특정 time step에서 노으지가 있는 이미지를 입력 받아 예측된 noise를 반환해야 한다. 예측된 노이즈는 입력 이미지와 동일한 크기/해상도를 갖는 tensor이다. 따라서 기술적으로 신경망은 동일한 shape의 텐서를 입력하고 출력한다. 이것을 위해 어떤 유형의 신경망을 사용할 수 있는가?
여기서 일반적으로 사용되는 것은 Autoencoder와 매우 유사하다. ‘intro to deep learning’ 튜토리얼을 떠올려라. autoencoder는 encoder와 decoder 사이에 소위 ‘bottleneck’ 레이어를 갖는다. 인코더는 우선 이미지를 ‘병목’이라 부르는 더 작은 은닉 표현으로 인코딩 하고 그 다음 디코더는 그 은닉 잠재 표현에서 실제 이미지를 디코딩 한다. 이것은 신경망이 병목 레이어에서 가장 중요한 정보만 유지하도록 강제한다.
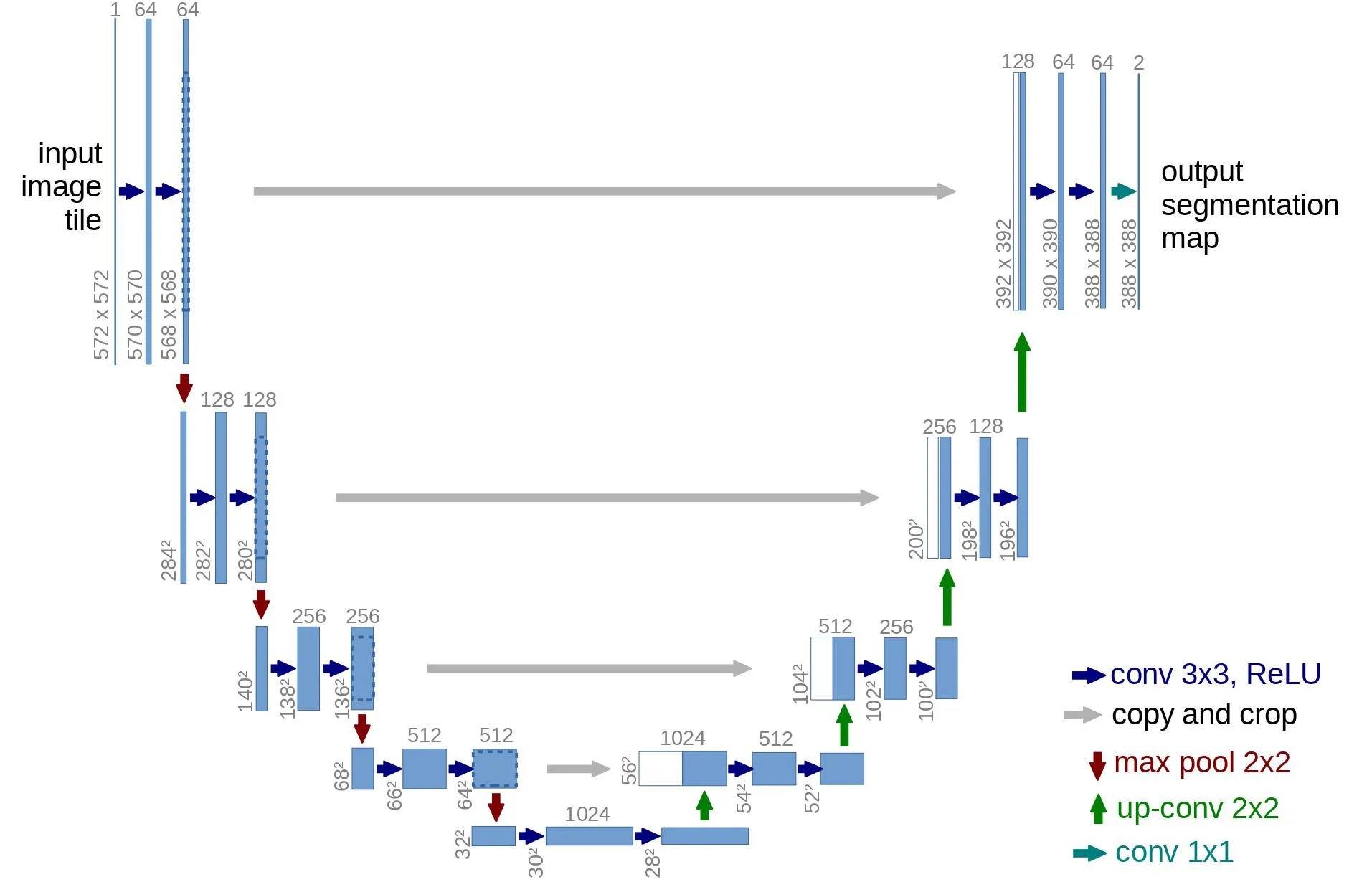
아키텍쳐 측면에서 DDPM 저자는 Ronneberger et al., 2015)에 의해 소개된 U-Net을 사용했다. (그 당시 의료 이미지 segmentation에 대해 최신 결과를 달성했음)
이 네트워크는 다른 autoencoder와 마찬가지로 네트워크가 가장 중요한 정보만 학습하도록 중간에 병목을 구성한다. 중요한 점은 인코더와 디코더 사이에 residual connection을 도입하여 gradient flow를 크게 개선했다는 점이다.
보시다시피 U-Net 모델은 우선 입력을 downsampling 하고(즉 공간 해상도 측면에서 입력을 더 작게 만든다) 그 후에 upsampling을 수행한다.
아래 이 네트워크를 단계별로 구현한다.
Network helpers
우선 신경망을 구현할 때 사용되는 helper 함수와 클래스를 정의한다. 중요한 것은 특정 함수의 출력에 입력을 추가하는 (즉 특정 함수에 residual connection을 추가하는) Residual 모듈을 정의하는 것이다.
또한 up과 downsampling 연산에 대한 별칭도 정의한다.
def exists(x):
return x is not None
def default(val, d):
if exists(val):
return val
return d() if isfunction(d) else d
def num_to_groups(num, divisor):
groups = num // divisor
remainder = num % divisor
arr = [divisor] * groups
if remainder > 0:
arr.append(remainder)
return arr
class Residual(nn.Module):
def __init__(self, fn):
super().__init__()
self.fn = fn
def forward(self, x, *args, **kwargs):
return self.fn(x, *args, **kwargs) + x
def Upsample(dim, dim_out=None):
return nn.Sequential(
nn.Upsample(scale_factor=2, mode="nearest"),
nn.Conv2d(dim, default(dim_out, dim), 3, padding=1),
)
def Downsample(dim, dim_out=None):
# No More Strided Convolutions or Pooling
return nn.Sequential(
Rearrange("b c (h p1) (w p2) -> b (c p1 p2) h w", p1=2, p2=2),
nn.Conv2d(dim * 4, default(dim_out, dim), 1),
)
Python
복사
Position embeddings
신경망의 파라미터가 시간(노이즈 레벨)에 걸쳐 공유되므로 저자들은 Transformer에서 영감 받은 sinusoidal position embedding을 이용하여 를 인코딩한다. 이것은 신경망이 배치의 각 이미지에 대해 특정 time step(노이즈 레벨)에서 작동하고 있는지 ‘알 수 있다’
SinuoidalPositionEmbeding 모듈은 (batch_size, 1)의 shape의 텐서를 입력(즉 배치에 포함된 여러 노이즈 이미지의 노이즈 레벨)으로 취하고, 이것을 position 임베딩의 차원 dim과 함께 (batch_size, dim) shape의 텐서로 변환한다. 그 다음 더 자세히 살펴보겠지만 이것은 각 residual block에 추가된다.
class SinusoidalPositionEmbeddings(nn.Module):
def __init__(self, dim):
super().__init__()
self.dim = dim
def forward(self, time):
device = time.device
half_dim = self.dim // 2
embeddings = math.log(10000) / (half_dim - 1)
embeddings = torch.exp(torch.arange(half_dim, device=device) * -embeddings)
embeddings = time[:, None] * embeddings[None, :]
embeddings = torch.cat((embeddings.sin(), embeddings.cos()), dim=-1)
return embeddings
Python
복사
ResNet block
다음으로 U-Net 모델의 핵심 building block을 정의한다. DDPM 저자들은 Wide ResNet block을 사용했지만 Phil Wang은 표준 convolutional 레이어를 ‘weighted standardized’ 버전으로 교체했다. 이것은 group normalization과 함께 더 잘 작동한다.
class WeightStandardizedConv2d(nn.Conv2d):
"""
https://arxiv.org/abs/1903.10520
weight standardization purportedly works synergistically with group normalization
"""
def forward(self, x):
eps = 1e-5 if x.dtype == torch.float32 else 1e-3
weight = self.weight
mean = reduce(weight, "o ... -> o 1 1 1", "mean")
var = reduce(weight, "o ... -> o 1 1 1", partial(torch.var, unbiased=False))
normalized_weight = (weight - mean) / (var + eps).rsqrt()
return F.conv2d(
x,
normalized_weight,
self.bias,
self.stride,
self.padding,
self.dilation,
self.groups,
)
class Block(nn.Module):
def __init__(self, dim, dim_out, groups=8):
super().__init__()
self.proj = WeightStandardizedConv2d(dim, dim_out, 3, padding=1)
self.norm = nn.GroupNorm(groups, dim_out)
self.act = nn.SiLU()
def forward(self, x, scale_shift=None):
x = self.proj(x)
x = self.norm(x)
if exists(scale_shift):
scale, shift = scale_shift
x = x * (scale + 1) + shift
x = self.act(x)
return x
class ResnetBlock(nn.Module):
"""https://arxiv.org/abs/1512.03385"""
def __init__(self, dim, dim_out, *, time_emb_dim=None, groups=8):
super().__init__()
self.mlp = (
nn.Sequential(nn.SiLU(), nn.Linear(time_emb_dim, dim_out * 2))
if exists(time_emb_dim)
else None
)
self.block1 = Block(dim, dim_out, groups=groups)
self.block2 = Block(dim_out, dim_out, groups=groups)
self.res_conv = nn.Conv2d(dim, dim_out, 1) if dim != dim_out else nn.Identity()
def forward(self, x, time_emb=None):
scale_shift = None
if exists(self.mlp) and exists(time_emb):
time_emb = self.mlp(time_emb)
time_emb = rearrange(time_emb, "b c -> b c 1 1")
scale_shift = time_emb.chunk(2, dim=1)
h = self.block1(x, scale_shift=scale_shift)
h = self.block2(h)
return h + self.res_conv(x)
Python
복사
Attention module
다음으로 attention module을 정의한다. DDPM 저자들은 이것을 convolution block 사이에 추가했다. attention은 유명한 Transformer 아키텍쳐의 빌딩 블록으로 NLP와 단밸질 접힘에 대한 vision 등 AI의 다양한 도메인에서 훌륭한 성공을 보여줬다. Phil Wang은 attention의 2가지 변종을 사용했다. 하나는 regular multi-head self-attention(Transformer에서 사용된)이고 다른 하나는 linear attention variant이다. 이것은 regular attention에서는 2차적인 시간과 메모리 요구 사항을 시퀀스 길이에 따라 선형으로 만든다.
class Attention(nn.Module):
def __init__(self, dim, heads=4, dim_head=32):
super().__init__()
self.scale = dim_head**-0.5
self.heads = heads
hidden_dim = dim_head * heads
self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)
self.to_out = nn.Conv2d(hidden_dim, dim, 1)
def forward(self, x):
b, c, h, w = x.shape
qkv = self.to_qkv(x).chunk(3, dim=1)
q, k, v = map(
lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
)
q = q * self.scale
sim = einsum("b h d i, b h d j -> b h i j", q, k)
sim = sim - sim.amax(dim=-1, keepdim=True).detach()
attn = sim.softmax(dim=-1)
out = einsum("b h i j, b h d j -> b h i d", attn, v)
out = rearrange(out, "b h (x y) d -> b (h d) x y", x=h, y=w)
return self.to_out(out)
class LinearAttention(nn.Module):
def __init__(self, dim, heads=4, dim_head=32):
super().__init__()
self.scale = dim_head**-0.5
self.heads = heads
hidden_dim = dim_head * heads
self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)
self.to_out = nn.Sequential(nn.Conv2d(hidden_dim, dim, 1),
nn.GroupNorm(1, dim))
def forward(self, x):
b, c, h, w = x.shape
qkv = self.to_qkv(x).chunk(3, dim=1)
q, k, v = map(
lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
)
q = q.softmax(dim=-2)
k = k.softmax(dim=-1)
q = q * self.scale
context = torch.einsum("b h d n, b h e n -> b h d e", k, v)
out = torch.einsum("b h d e, b h d n -> b h e n", context, q)
out = rearrange(out, "b h c (x y) -> b (h c) x y", h=self.heads, x=h, y=w)
return self.to_out(out)
Python
복사
Group normalization
DDPM 저자들은 U-Net의 convolutional/attention 레이어를 group normalization과 함께 교차한다. 아래에서는 attention 레이어 전에 groupnorm을 적용하는데 사용되는 PreNorm 클래스를 정의한다. Transformer에서는 normalization을 attention 전 또는 후에 적용하는 것에 대한 논쟁이 존재한다.
class PreNorm(nn.Module):
def __init__(self, dim, fn):
super().__init__()
self.fn = fn
self.norm = nn.GroupNorm(1, dim)
def forward(self, x):
x = self.norm(x)
return self.fn(x)
Python
복사
Conditional U-Net
이제 모든 빌딩 블록(position embedding, ResNet blocks, attention, group normalization)을 정의했으므로, 전체 신경망을 정의할 시간이다. 네트워크 의 작업이 noisy 이미지의 배치와 그들의 노이즈 레벨을 취하고 입력에 추가된 노이즈를 출력하는 것임을 떠올려라. 더 형식적으로
•
네트워크는 (batch_size, num_channels, height, width) shape의 noisy 이미지의 배치와 (batch_size, 1) shape의 노이즈 레벨의 배치를 입력으로 취하고 (batch_size, num_channels, height, width) shape의 tensor를 반환한다.
네트워크는 다음과 같이 구축된다.
•
우선 convolutional 레이어는 noisy 이미지의 배치에 적용되고 position embedding은 noise 레벨에 대해 계산된다.
•
다음으로 downsampling stage의 시퀀스가 적용된다. 각 downsampling 단계는 2개의 ResNet block + group norm + attention + residual connection + downsample 연산으로 구성된다.
•
네트워크의 중간에서 ResNet 블록이 다시 적용된다. attention과 함께 교차된다.
•
다음으로 upsampling 단계의 시퀀스가 적용된다. 각 upsampling 단계는 2개 ResNet block + group norm + attention + residual connection + upsampling 연산으로 구성된다.
•
마지막으로 ResNet block과 convolutional 레이어가 적용된다.
궁극적으로 신경망은 레고 블록처럼 layer를 쌓아 올린다.
class Unet(nn.Module):
def __init__(
self,
dim,
init_dim=None,
out_dim=None,
dim_mults=(1, 2, 4, 8),
channels=3,
self_condition=False,
resnet_block_groups=4,
):
super().__init__()
# determine dimensions
self.channels = channels
self.self_condition = self_condition
input_channels = channels * (2 if self_condition else 1)
init_dim = default(init_dim, dim)
self.init_conv = nn.Conv2d(input_channels, init_dim, 1, padding=0) # changed to 1 and 0 from 7,3
dims = [init_dim, *map(lambda m: dim * m, dim_mults)]
in_out = list(zip(dims[:-1], dims[1:]))
block_klass = partial(ResnetBlock, groups=resnet_block_groups)
# time embeddings
time_dim = dim * 4
self.time_mlp = nn.Sequential(
SinusoidalPositionEmbeddings(dim),
nn.Linear(dim, time_dim),
nn.GELU(),
nn.Linear(time_dim, time_dim),
)
# layers
self.downs = nn.ModuleList([])
self.ups = nn.ModuleList([])
num_resolutions = len(in_out)
for ind, (dim_in, dim_out) in enumerate(in_out):
is_last = ind >= (num_resolutions - 1)
self.downs.append(
nn.ModuleList(
[
block_klass(dim_in, dim_in, time_emb_dim=time_dim),
block_klass(dim_in, dim_in, time_emb_dim=time_dim),
Residual(PreNorm(dim_in, LinearAttention(dim_in))),
Downsample(dim_in, dim_out)
if not is_last
else nn.Conv2d(dim_in, dim_out, 3, padding=1),
]
)
)
mid_dim = dims[-1]
self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)
self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim)))
self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)
for ind, (dim_in, dim_out) in enumerate(reversed(in_out)):
is_last = ind == (len(in_out) - 1)
self.ups.append(
nn.ModuleList(
[
block_klass(dim_out + dim_in, dim_out, time_emb_dim=time_dim),
block_klass(dim_out + dim_in, dim_out, time_emb_dim=time_dim),
Residual(PreNorm(dim_out, LinearAttention(dim_out))),
Upsample(dim_out, dim_in)
if not is_last
else nn.Conv2d(dim_out, dim_in, 3, padding=1),
]
)
)
self.out_dim = default(out_dim, channels)
self.final_res_block = block_klass(dim * 2, dim, time_emb_dim=time_dim)
self.final_conv = nn.Conv2d(dim, self.out_dim, 1)
def forward(self, x, time, x_self_cond=None):
if self.self_condition:
x_self_cond = default(x_self_cond, lambda: torch.zeros_like(x))
x = torch.cat((x_self_cond, x), dim=1)
x = self.init_conv(x)
r = x.clone()
t = self.time_mlp(time)
h = []
for block1, block2, attn, downsample in self.downs:
x = block1(x, t)
h.append(x)
x = block2(x, t)
x = attn(x)
h.append(x)
x = downsample(x)
x = self.mid_block1(x, t)
x = self.mid_attn(x)
x = self.mid_block2(x, t)
for block1, block2, attn, upsample in self.ups:
x = torch.cat((x, h.pop()), dim=1)
x = block1(x, t)
x = torch.cat((x, h.pop()), dim=1)
x = block2(x, t)
x = attn(x)
x = upsample(x)
x = torch.cat((x, r), dim=1)
x = self.final_res_block(x, t)
return self.final_conv(x)
Python
복사
Defining the forward diffusion process
forward diffusion 프로세스는 time step 로 실제 분포에서 점진적으로 이미지에 노이즈를 추가한다. 이것은 분산 스케쥴을 따라 일어난다. 원래의 DDPM 저자는 선형 스케쥴을 사용했었다.
우리는 forward 프로세스 분산을 에서 까지 선형으로 일정하게 증가하도록 설정했다.
그러나 (Nichole et al., 2021)에서 cosine 스케쥴을 사용할 때 더 나은 결과를 얻을 수 있음이 드러났다.
아래 timestep에 대한 다양한 스케쥴을 정의한다. (나중에 하나 선택한다)
def cosine_beta_schedule(timesteps, s=0.008):
"""
cosine schedule as proposed in https://arxiv.org/abs/2102.09672
"""
steps = timesteps + 1
x = torch.linspace(0, timesteps, steps)
alphas_cumprod = torch.cos(((x / timesteps) + s) / (1 + s) * torch.pi * 0.5) ** 2
alphas_cumprod = alphas_cumprod / alphas_cumprod[0]
betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1])
return torch.clip(betas, 0.0001, 0.9999)
def linear_beta_schedule(timesteps):
beta_start = 0.0001
beta_end = 0.02
return torch.linspace(beta_start, beta_end, timesteps)
def quadratic_beta_schedule(timesteps):
beta_start = 0.0001
beta_end = 0.02
return torch.linspace(beta_start**0.5, beta_end**0.5, timesteps) ** 2
def sigmoid_beta_schedule(timesteps):
beta_start = 0.0001
beta_end = 0.02
betas = torch.linspace(-6, 6, timesteps)
return torch.sigmoid(betas) * (beta_end - beta_start) + beta_start
Python
복사
우선 time step에 대한 선형 스케쥴을 사용하고 분산의 누적 곱 과 같이 에서 필요한 다양한 변수를 정의한다. 아래의 각 변수는 1차원 텐서이며 에서 까지 값을 저장한다. 중요한 것은 extract function을 정의하여 인덱스의 배치에 대해 적절한 인덱스를 추출할 수 있다는 것이다.
timesteps = 300
# define beta schedule
betas = linear_beta_schedule(timesteps=timesteps)
# define alphas
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, axis=0)
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)
sqrt_recip_alphas = torch.sqrt(1.0 / alphas)
# calculations for diffusion q(x_t | x_{t-1}) and others
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)
sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)
# calculations for posterior q(x_{t-1} | x_t, x_0)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)
def extract(a, t, x_shape):
batch_size = t.shape[0]
out = a.gather(-1, t.cpu())
return out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device)
Python
복사
diffusion 프로세스의 각 time step에서 노이즈가 어떻게 추가되는지를 고양이 이미지를 이용하여 설명한다.
from PIL import Image
import requests
url = 'http://images.cocodataset.org/val2017/000000039769.jpg'
image = Image.open(requests.get(url, stream=True).raw) # PIL image of shape HWC
image
Python
복사
노이즈는 Pillow Image 대신 PyTorch Tensor에 추가된다. 우선 PIL 이미지에서 PyTorch 텐서로(노이즈를 추가할 수 있는 텐서)로 또는 그 반대로 이미지 변환을 정의한다.
이 변환은 꽤 간단하다. 우선 255로 나누어 이미지를 정규화한 다음 ( 범위에 놓이도록) 그 다음 범위에 놓이게 한다. DDPM 논문에서
이미지 데이터가 까지 선형적으로 스케일링된 의 정수로 구성된다고 가정한다. 이것은 신경망 reverse 프로세스가 표준 정규 prior 에서 시작하여 일관되게 스케일링된 입력에서 작동하도록 보장한다.
from torchvision.transforms import Compose, ToTensor, Lambda, ToPILImage, CenterCrop, Resize
image_size = 128
transform = Compose([
Resize(image_size),
CenterCrop(image_size),
ToTensor(), # turn into torch Tensor of shape CHW, divide by 255
Lambda(lambda t: (t * 2) - 1),
])
x_start = transform(image).unsqueeze(0)
x_start.shape
Python
복사
또한 안에 값을 포함하는 PyTorch 텐서를 PIL 이미지로 되돌리는 reverse 변환을 정의한다.
import numpy as np
reverse_transform = Compose([
Lambda(lambda t: (t + 1) / 2),
Lambda(lambda t: t.permute(1, 2, 0)), # CHW to HWC
Lambda(lambda t: t * 255.),
Lambda(lambda t: t.numpy().astype(np.uint8)),
ToPILImage(),
])
Python
복사
이제 논문에서와 같이 forward diffusion 프로세스를 정의할 수 있다.
# forward diffusion (using the nice property)
def q_sample(x_start, t, noise=None):
if noise is None:
noise = torch.randn_like(x_start)
sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape)
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x_start.shape
)
return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise
Python
복사
특정 time step에서 테스트 할 수 있다.
def get_noisy_image(x_start, t):
# add noise
x_noisy = q_sample(x_start, t=t)
# turn back into PIL image
noisy_image = reverse_transform(x_noisy.squeeze())
return noisy_image
Python
복사
# take time step
t = torch.tensor([40])
get_noisy_image(x_start, t)
Python
복사
다양한 time step에 대해 시각화할 수 있다.
import matplotlib.pyplot as plt
# use seed for reproducability
torch.manual_seed(0)
# source: https://pytorch.org/vision/stable/auto_examples/plot_transforms.html#sphx-glr-auto-examples-plot-transforms-py
def plot(imgs, with_orig=False, row_title=None, **imshow_kwargs):
if not isinstance(imgs[0], list):
# Make a 2d grid even if there's just 1 row
imgs = [imgs]
num_rows = len(imgs)
num_cols = len(imgs[0]) + with_orig
fig, axs = plt.subplots(figsize=(200,200), nrows=num_rows, ncols=num_cols, squeeze=False)
for row_idx, row in enumerate(imgs):
row = [image] + row if with_orig else row
for col_idx, img in enumerate(row):
ax = axs[row_idx, col_idx]
ax.imshow(np.asarray(img), **imshow_kwargs)
ax.set(xticklabels=[], yticklabels=[], xticks=[], yticks=[])
if with_orig:
axs[0, 0].set(title='Original image')
axs[0, 0].title.set_size(8)
if row_title is not None:
for row_idx in range(num_rows):
axs[row_idx, 0].set(ylabel=row_title[row_idx])
plt.tight_layout()
Python
복사
plot([get_noisy_image(x_start, torch.tensor([t])) for t in [0, 50, 100, 150, 199]])
Python
복사
이것은 모델이 주어지면 loss 함수를 다음처럼 정의할 수 있다는 뜻이다.
def p_losses(denoise_model, x_start, t, noise=None, loss_type="l1"):
if noise is None:
noise = torch.randn_like(x_start)
x_noisy = q_sample(x_start=x_start, t=t, noise=noise)
predicted_noise = denoise_model(x_noisy, t)
if loss_type == 'l1':
loss = F.l1_loss(noise, predicted_noise)
elif loss_type == 'l2':
loss = F.mse_loss(noise, predicted_noise)
elif loss_type == "huber":
loss = F.smooth_l1_loss(noise, predicted_noise)
else:
raise NotImplementedError()
return loss
Python
복사
denoise_model은 위에 정의된 U-Net이다. 실제와 예측된 노이즈 사이에 Huber loss를 사용한다.
Define a PyTorch Dataset + DataLoader
여기서 일반 PyTorch 데이터셋을 정의한다. 데이터셋은 단순히 Fashion-MNIST, CIFAR-10이나 ImageNet과 같은 실제 데이터셋의 이미지로 구성되며 으로 선형으로 스케일한다.
각 이미지는 같은 크기로 resize 된다. 흥미로운 부분은 이미지가 랜덤으로 수평으로 뒤집힌다는 것이다. 논문에서
CIFAR10에 대해 학습한느 동안 무작위로 수평 flip을 사용했다. flip 유무에 관계 없이 학습을 시도한 결과 flip이 샘플 품질을 약간 향상 시키는 것으로 나타났다.
여기서 Dataset library를 사용하여 hub에서 Fashion MNIST 데이터셋을 쉽게 로드할 수 있다. 이 데이터셋은 28x28의 동일한 해상도를 갖는 이미지로 구성되어 있다.
from datasets import load_dataset
# load dataset from the hub
dataset = load_dataset("fashion_mnist")
image_size = 28
channels = 1
batch_size = 128
Python
복사
다음으로 전체 데이터셋에 대해 on-the-fly(즉시) 적용할 함수를 정의한다. 이를 위해 with_transform 함수를 사용한다. 이 함수는 기본 이미지 전처리(무작위 수평 뒤집기, rescaling)을 적용하고 마지막으로 범위에 값을 놓는다.
from torchvision import transforms
from torch.utils.data import DataLoader
# define image transformations (e.g. using torchvision)
transform = Compose([
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Lambda(lambda t: (t * 2) - 1)
])
# define function
def transforms(examples):
examples["pixel_values"] = [transform(image.convert("L")) for image in examples["image"]]
del examples["image"]
return examples
transformed_dataset = dataset.with_transform(transforms).remove_columns("label")
# create dataloader
dataloader = DataLoader(transformed_dataset["train"], batch_size=batch_size, shuffle=True)
Python
복사
batch = next(iter(dataloader))
print(batch.keys())
Python
복사
Sampling
학습 하는 동안 (진행을 추적하는 측면에서) 모델에서 샘플하기 위한 코드를 아래 코드를 정의한다. 샘플링은 논문에서 Algorithm 2로 요약되어 있다.
diffusion 모델에서 새로운 이미지를 생성하는 것은 diffusion 프로세스를 reversing 하여 한다. 에서 시작하고 여기서 가우시안 분포에서 순수 노이즈를 샘플한다. 그 다음 신경망을 사용하여 학습된 조건부 확률을 사용하여 time step 가 될 때까지 점진적으로 denoise 한다. 위에 보인대로 노이즈 예측기를 사용하여 평균의 reparametrization에 연결하면 약간 덜 denoise 된 이미지 을 유도할 수 있다. 분산은 미리 알려져 있다는 것을 떠올려라.
이상적으로는 실제 데이터 분포에서 온 것처럼 보이는 이미지가 완성된다.
이것을 구현 코드는 아래 참조.
@torch.no_grad()
def p_sample(model, x, t, t_index):
betas_t = extract(betas, t, x.shape)
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x.shape
)
sqrt_recip_alphas_t = extract(sqrt_recip_alphas, t, x.shape)
# Equation 11 in the paper
# Use our model (noise predictor) to predict the mean
model_mean = sqrt_recip_alphas_t * (
x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t
)
if t_index == 0:
return model_mean
else:
posterior_variance_t = extract(posterior_variance, t, x.shape)
noise = torch.randn_like(x)
# Algorithm 2 line 4:
return model_mean + torch.sqrt(posterior_variance_t) * noise
# Algorithm 2 (including returning all images)
@torch.no_grad()
def p_sample_loop(model, shape):
device = next(model.parameters()).device
b = shape[0]
# start from pure noise (for each example in the batch)
img = torch.randn(shape, device=device)
imgs = []
for i in tqdm(reversed(range(0, timesteps)), desc='sampling loop time step', total=timesteps):
img = p_sample(model, img, torch.full((b,), i, device=device, dtype=torch.long), i)
imgs.append(img.cpu().numpy())
return imgs
@torch.no_grad()
def sample(model, image_size, batch_size=16, channels=3):
return p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))
Python
복사
위의 코드는 원본 구현의 단순화된 버전임에 유의하라. 이 단순화 버전이 clipping을 사용하는 더 복잡한 원본의 구현과 똑같이 잘 작동한다는 사실을 발견했다.
Train the model
다음으로 일반 PyTorch 방식으로 모델을 학습한다. 또한 위에 정의된 sample 메서드를 사용하여 주기적으로 생성된 이미지를 저장하는 로직을 추가한다.
from pathlib import Path
def num_to_groups(num, divisor):
groups = num // divisor
remainder = num % divisor
arr = [divisor] * groups
if remainder > 0:
arr.append(remainder)
return arr
results_folder = Path("./results")
results_folder.mkdir(exist_ok = True)
save_and_sample_every = 1000
Python
복사
아래에 모델을 정의하고 GPU로 이동한다. 또한 표준 optimizer(Adam)을 정의한다.
from torch.optim import Adam
device = "cuda" if torch.cuda.is_available() else "cpu"
model = Unet(
dim=image_size,
channels=channels,
dim_mults=(1, 2, 4,)
)
model.to(device)
optimizer = Adam(model.parameters(), lr=1e-3)
Python
복사
학습을 시작한다.
from torchvision.utils import save_image
epochs = 6
for epoch in range(epochs):
for step, batch in enumerate(dataloader):
optimizer.zero_grad()
batch_size = batch["pixel_values"].shape[0]
batch = batch["pixel_values"].to(device)
# Algorithm 1 line 3: sample t uniformally for every example in the batch
t = torch.randint(0, timesteps, (batch_size,), device=device).long()
loss = p_losses(model, batch, t, loss_type="huber")
if step % 100 == 0:
print("Loss:", loss.item())
loss.backward()
optimizer.step()
# save generated images
if step != 0 and step % save_and_sample_every == 0:
milestone = step // save_and_sample_every
batches = num_to_groups(4, batch_size)
all_images_list = list(map(lambda n: sample(model, batch_size=n, channels=channels), batches))
all_images = torch.cat(all_images_list, dim=0)
all_images = (all_images + 1) * 0.5
save_image(all_images, str(results_folder / f'sample-{milestone}.png'), nrow = 6)
Python
복사
Sampling (inference)
이 모델에서 샘플링하기 위해 위의 정의된 sample 함수를 사용할 수 있다.
# sample 64 images
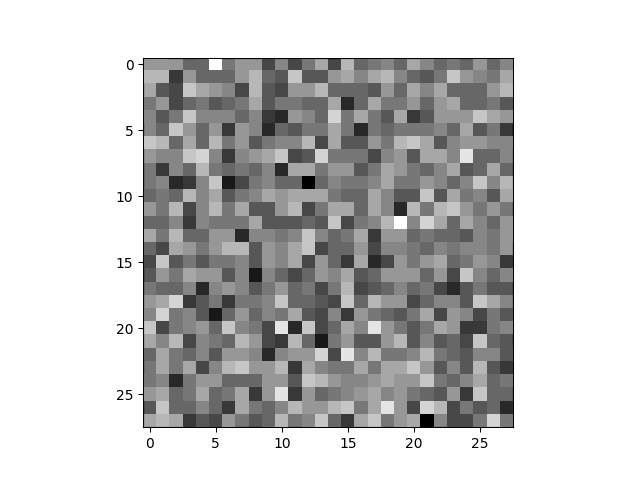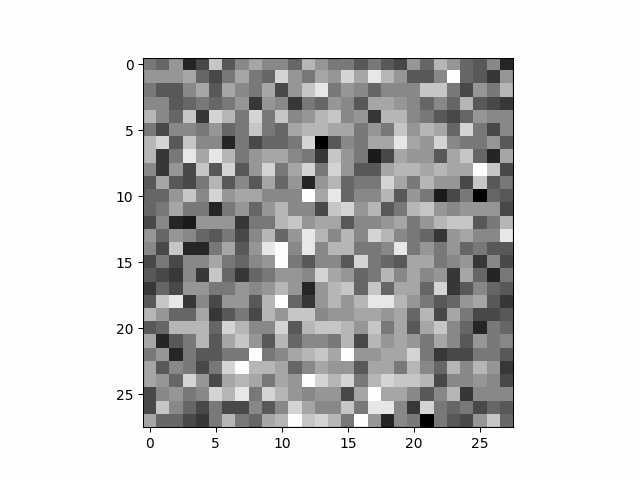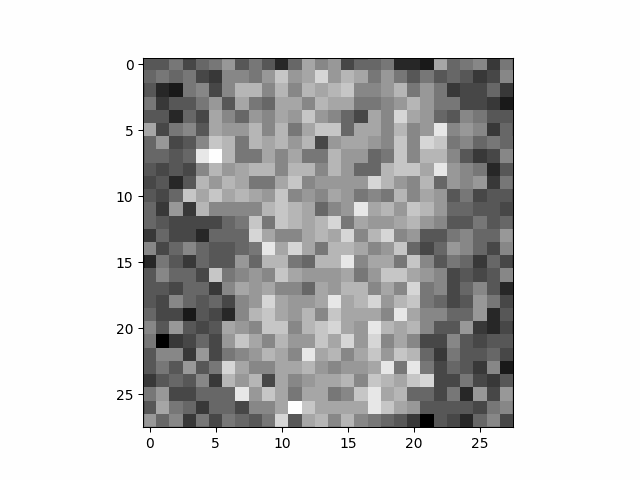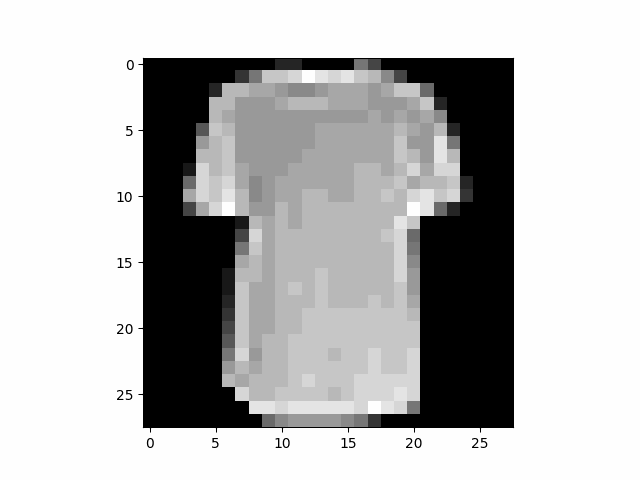
samples = sample(model, image_size=image_size, batch_size=64, channels=channels)
# show a random one
random_index = 5
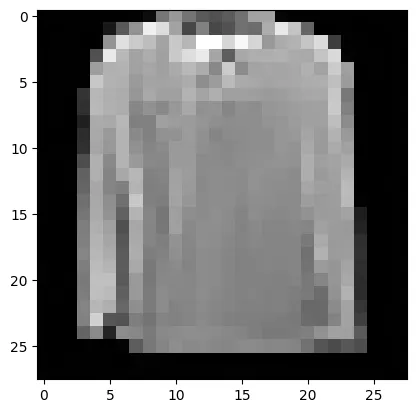
plt.imshow(samples[-1][random_index].reshape(image_size, image_size, channels), cmap="gray")
Python
복사
모델이 훌륭한 T-shirt를 생성할 능력이 있는 것으로 보인다. 학습한 데이터셋의 해상도가 매우 낮다는 점을 떠올려라(28x28)
또한 denoising 프로세스의 git를 만들 수도 있다.
import matplotlib.animation as animation
random_index = 53
fig = plt.figure()
ims = []
for i in range(timesteps):
im = plt.imshow(samples[i][random_index].reshape(image_size, image_size, channels), cmap="gray", animated=True)
ims.append([im])
animate = animation.ArtistAnimation(fig, ims, interval=50, blit=True, repeat_delay=1000)
animate.save('diffusion.gif')
plt.show()
Python
복사
Follow-up reads
DDPM 논문은 diffusion 모델이 (un)conditional 이미지 생성에 유망한 방향임을 보였다. 그 이후로 (엄청나게) 개선되었으며 특히 text-conditional 이미지 생성에 대해 주목할만 했다. 아래 중요한 (그러나 완전하지는 않은) follow-up 작업이 나열되어 있다.
•
•
•
•
•
•
Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding (ImageGen) (Saharia et al., 2022)
이것은 글이 작성된 시점인 2022년 6월 7일까지의 중요한 것만 포함되어 있다.
현재로써 diffusion 모델의 주된(아마도 유일한) 단점은 이미지를 생성하는데 여러 번의 forward pass가 필요하다는 것이다. (GAN 같은 생성 모델의 경우 그렇지 않음) 하지만 노이즈 제거 단계가 10 단계에 불과한 높은 fidelity 생성 연구가 진행 중이다.