Search
Duplicate

AI/ Paper/ Consistency Model

Consistency Models
Diffusion models have significantly advanced the fields of image, audio, and video generation, but they depend on an iterative sampling process that causes slow generation. To overcome this...
https://arxiv.org/abs/2303.01469

Abstract

Diffusion model은 이미지, 오디오, 비디오 생성 분야를 크게 발전 시켰지만 생성을 느리게 하는 원인인 반복 샘플링 절차에 의존한다. 이 한계를 극복하기 위해 우리는 consistency model을 제안한다. 이것은 노이즈를 데이터에 직접 매핑하여 높은 품질의 샘플을 생성하는 모델의 새로운 계열이다. 그것은 설계 상 빠른 one-step 생성을 지원하며 샘플 품질과 계산에 대한 tradeoff를 위해 multistep 샘플링을 허용한다. 또한 image inpainting, colorization, super-resolution 등의 zero-shot 데이터 편집을 지원하며 이런 작업에 대한 명시적 학습이 필요하지 않다. Consistency 모델은 pretrained diffusion 모델을 distiling 하거나 standalone 생성 모델로 학습될 수 있다. 광범위한 실험을 통해 우리는 consistency 모델이 기존 diffusion 모델 distilling 기법보다 우수한 성능을 보임을 입증했다. CIFAR-10에서 3.55, ImageNet 64x64에서 6.20의 최신 단계 생성 FID 기록을 달성했다. 독립적으로 학습된 consistency 모델은 기존의 one-step, non-adversarial 생성 모델보다 CIFAR-10, ImageNet 64x64, LSUN 256x256 등의 벤치마크에서 우수한 성능을 보이는 새로운 생성 모델 계열이다.

1 Introduction

Diffusion 모델은 score-based 생성 모델이라고도 불리며 이미지 생성, 오디오 합성과 비디오 생성을 포함하여 여러 영역에 걸쳐 unprecedented(전례 없는) 성공을 달성했다. diffusion 모델의 핵심 기능은 반복적 샘플링 프로세스을 통해 무작위 초기 벡터에서 노이즈를 제거한다는 것이다. 이 반복 프로세스는 계산과 샘플 퀄리티 사이의 유연한 trade-off를 제공한다. 더 많은 반복 계산을 수행할 수록 일반적으로 더 나은 품질의 샘플을 산출할 수 있다. 이것은 또한 image inpainting, colorization, stroke-guided image 편집, 전산화 단층 촬영, 자기공명영상 등 다양한 도전적인 inverse 문제를 해결할 수 있는 diffusion 모델의 zero-shot 데이터 편집 능력의 crux(핵심)이다. 그러나 GAN, VAE나 normalizing flow 같은 단일 단계 생성 모델과 비교하여 diffusion 모델의 반복적 생성 절차는 일반적으로 샘플 생성을 위해 10-2000배 더 많은 계산이 필요하다. 이것은 느린 추론과 제한된 실시간 응용을 갖는다.
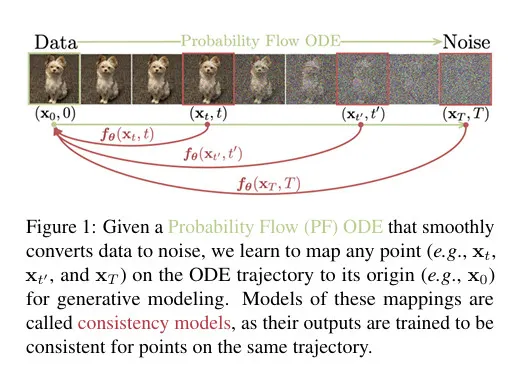
우리의 목표는 필요한 경우 계산 비용과 샘플 퀄리티에 대한 tradeoff가 가능하게 하고, zero-shot 데이터 편집 작업을 수행할 수 있는 반복적 샘플링의 중요한 장점을 희생하지 않으면서 효율적인 단일 단계 생성을 가능하게 하는 생성 모델을 만드는 것이다. 그림 1 참조. 우리는 연속 시간 diffusion 모델의 Probability Flow(PF) Ordinary Differential Equation (ODE)을 기반으로 한다. 이 궤적은 데이터 분포를 부드럽게 tractable 노이즈 분포로 전환한다. 우리는 임의의 시간 단계에서 궤적의 시작점에 매핑하는 모델을 학습할 것을 제안한다. 우리 모델의 주목할만한 속성은 self-consistency이다. 동일한 궤적 상의 점들은 동일한 초기 점으로 매핑 된다. 따라서 우리는 이러한 모델을 consistency model이라 부른다. consistency 모델을 통해 무작위 노이즈 벡터(ODE 궤적의 끝점, 예 그림 1의 xT\bold{x}_T)를 단일 네트워크 평가로 변환하여 데이터 샘플(ODE의 초기 포인트 궤적, 예 그림 1의 x1\bold{x}_1)을 생성할 수 있다. 중요한 점은 여러 시간 단계에서 consistency 모델의 출력을 chaining 하면 더 많은 계산 비용으로 샘플 품질을 개선하고 zero-shot 데이터 편집을 수행할 수 있다는 것이다. 이는 diffusion 모델의 반복적 샘플링과 유사하다.
consistency 모델을 학습하기 위해 self-consistency 속성을 강화하는데 기반한 두 가지 방법을 제안한다. 첫 번째 방법은 수치적 ODE solver와 pre-trained diffusion 모델을 사용하여 PF ODE 궤적 상의 인접한 점의 쌍을 생성하는 것이다. 이 쌍에 대한 모델의 출력 차이를 최소화하여 diffusion 모델을 효과적으로 consistency 모델로 distill 할 수 있고 이를 통해 단일 네트워크 평가를 사용하여 높은 품질의 샘플을 생성할 수 있다. 반면에 두 번째 방법은 pre-trained diffusion 모델을 제거하고 consistency 모델을 단독으로 학습한다. 이 접근은 consistency 모델을 독립적인 생성 모델로 만든다. 중요한 것은 어느 것도 adversarial 학습이 필요 하지 않고, 두 방법 모두 consistency 모델을 파라미터화 하기 위한 유연한 신경망의 사용을 허용하는 아키텍쳐에 작은 제약조건만 둔다는 것이다.
우리는 CIFAR-10, ImageNet 64x64, LSUN 256x256 등 여러 이미지 데이터셋에서 consistency 모델의 효율성을 입증한다. 경험적으로 distilling 접근으로 consistency 모델은 progressive distillation 같은 기존 diffusion 모델 distilling 방법 보다 다양한 데이터셋에서 few-step 생성 시 더 나은 성능을 보인다. CIFAR-10에서 consistency 모델은 one-step과 two-step 생성에 대해 각각 3.55와 2.93의 새로운 FID를 달성했다. ImageNet 64x64에서는 one-step과 two-step 네트워크 평가로 각각 6.20과 4.70의 기록적인 FID를 달성했다. 독립적인 생성 모델로 학습될 때, consistency 모델은 pretrained diffusion 모델에 대한 접근 없이도 progressive distilling의 one-step 샘플 품질과 동등하거나 그 이상의 성능을 낼 수 있다. 또한 다양한 데이터셋에 걸쳐 많은 GAN과 기존의 비적대적 단일 단계 생성 모델보다 우수한 성능을 보인다. 더불어 우리는 consistency 모델을 사용하여 image denoising, 보간, inpainting, colorization, super-resolution, stroke-guided image 편집 등 다양한 zero-shot 데이터 편집 작업을 수행할 수 있음을 보여준다.

2 Diffusion Models

Consistency 모델은 continuous-time diffusion model의 이론에 의해 크게 영향을 받았다. diffusion 모델은 데이터를 가우시안 교란을 통해 점차적으로 노이즈로 변환한 다음, 순차적인 denoising 단계를 통해 노이즈에서 샘플을 생성하는 방식으로 데이터를 생성 한다. pdata(x)p_\text{data}(\bold{x})를 데이터 분포라 표기하자. diffusion 모델은 Stochastic Differential Equation(SDE)를 사용하여 pdata(x)p_\text{data}(\bold{x})을 확산 시키는 것에서 시작한다.
dxt=μ(xt,t)dt+σ(t)dwt(1)d\bold{x}_t = \boldsymbol{\mu}(\bold{x}_t, t) dt + \sigma(t)d\bold{w}_t \tag{1}
여기서 t∈[0,T]t \in [0, T]이고 T>0T > 0은 고정된 상수이다. μ(⋅,⋅)\boldsymbol{\mu}(\cdot, \cdot)과 σ(⋅)\sigma(\cdot)은 각각 drift와 diffusion 계수이다. 그리고 {wt}t∈[0,T]\{\bold{w}_t\}_{t\in[0,T]}는 표준 Brownian motion을 표기한다. xt\bold{x}_t의 분포를 pt(x)p_t(\bold{x})라 표기하고 그 결과 p0(x)≡pdata(x)p_0(\bold{x}) \equiv p_\text{data}(\bold{x})가 된다. SDE의 주목할만한 특성은 Song et al(2021) 등이 Probability Flow(PF) ODE라 부른 Ordinary Differential Equation(ODE)이 존재한다는 것이다. 이 방정식의 tt에서 샘플된 솔루션의 궤적은 pt(x)p_t(\bold{x})를 따라 분포된다.
dxt=[μ(xt,t)−12σ(t)2∇log⁡pt(xt)]dt(2)d\bold{x}_t = \Big[ \boldsymbol{\mu}(\bold{x}_t, t) - {1\over2}\sigma(t)^2 \nabla \log p_t(\bold{x}_t) \Big] dt \tag{2}
여기서 ∇log⁡pt(x)\nabla \log p_t(\bold{x})는 pt(x)p_t(\bold{x})의 score 함수이다. 따라서 diffusion 모델은 score-based 생성 모델이라고도 한다.
일반적으로 방정식 1의 SDE는 pT(x)p_T(\bold{x})가 다루기 용이한 가우시안 분포 π(x)\pi(\bold{x})에 가까워지도록 설계된다. 여기서 Karras et al(2022)의 설정을 채택하여 μ(x,t)=0\boldsymbol{\mu}(\bold{x},t) = \bold{0}이고 σ(t)=2t\sigma(t) = \sqrt{2t}로 설정한다. 이 경우에 pt(x)=pdata(x)⊗N(0,t2I)p_t(\bold{x}) = p_\text{data}(\bold{x}) \otimes \mathcal{N}(\bold{0}, t^2\bold{I})이다. 여기서 ⊗\otimes는 convolution 연산이고 π(x)=N(0,T2I)\pi(\bold{x}) = \mathcal{N}(\bold{0},T^2\bold{I})이다. (π(x)\pi(\bold{x})는 xT\bold{x}_T의 샘플) 샘플링을 위해 우선 score 매칭을 통해 score 모델 sϕ(x,t)≈∇log⁡pt(x)s_{\boldsymbol{\phi}}(\bold{x}, t) \approx \nabla \log p_t(\bold{x})를 학습한 다음 방정식 2에 연결하여 다음 형식을 갖는 PF ODE의 경험적 추정을 얻는다.
dxtdt=−tsϕ(xt,t)(3){d\bold{x}_t \over dt} = -ts_\phi(\bold{x}_t, t) \tag{3}
방정식 3을 경험적 PF ODE라 부른다. 다음으로 경험적 PF ODE를 초기화하기 위해 x^T∼π=N(0,T2I)\hat{\bold{x}}_T \sim \pi = \mathcal{N}(\bold{0}, T^2\bold{I})를 샘플하고, Euler 또는 Heun 솔버 같은 임의의 수치적 ODE 솔버를 사용하여 시간을 거슬러가며 해 궤적 {x^t}t∈[0,T]\{\hat{\bold{x}}_t\}_{t \in [0, T]}을 구한다. 결과 x^0\hat{\bold{x}}_0는 데이터 분포 pdata(x)p_\text{data}(\bold{x})에서 근사 샘플로 볼 수 있다. 수치적 불안정성을 피하기 위해 일반적으로 t=ϵt = \epsilon에서 솔버를 멈춘다. 여기서 ϵ\epsilon은 작은 양의 상수이고 x^ϵ\hat{\bold{x}}_\epsilon을 근사 샘플로써 받아들인다. Karras et al(2022)을 따라 이미지 픽셀 값을 [−1,1][-1, 1]로 rescale하고 T=80,ϵ=0.002T = 80, \epsilon = 0.002로 설정한다.
Diffusion 모델은 느린 샘플링 속도가 병목이다. 분명히 ODE를 사용한 샘플링은 계산 비용이 많이 드는 score 모델 sϕ(x,t)s_{\boldsymbol{\phi}}(\bold{x}, t)의 반복적 평가가 필요하다. 빠른 샘플링을 위한 기존 방법에는 더 빠른 수치적 ODE 솔버와 distillation 기법 등이 있다. 그러나 ODE 솔버는 경쟁력 있는 샘플을 생성하기 위해 여전히 10 단계 이상의 평가가 필요하다. Luhman(2021)이나 Zheng et al(2022) 같은 대부분 distillation 방법은 distillation을 위해 diffusion 모델 prior에서 대규모 데이터셋에서 샘플을 수집해야 하는데 이 자체로 계산 비용이 많이 든다. 우리가 아는 한 이런 단점이 없는 유일한 distilling 접근은 progressive distillation(PD)이다. 우리는 실험에서 consistency 모델과 광범위하게 비교했다.

3 Consistency Models

우리는 consistency 모델을 제안한다. 이것은 샘플 품질과 계산 비용과 zero-shot 데이터 편집 사이의 tradeoff에 대한 반복적 생성을 허용하면서 설계의 핵심으로 단일 단계 생성을 지원하는 새로운 유형의 모델이다. Consistency 모델은 distillation 모드나 isolation 모드를 사용하여 학습될 수 있다. 전자의 경우 consistency 모델은 pre-trained diffusion 모델의 지식을 단일 단계 샘플러에 distill 한다. zero-shot 이미지 편집 응용을 허용하면서 샘플 품질 면에서 다른 distillation을 크게 개선한다. 후자의 경우에 consistency 모델은 pre-trained diffusion 모델에 의존하지 않고 단독으로 학습된다. 이것은 생성 모델의 독립적인 새로운 클래스을 만든다.
아래에서 consistency 모델의 정의, 파라미터화, 샘플링에 대해 소개한다. 추가로 zero-shot 데이터 편집에 대한 그것의 응용에 대해 간략히 소개한다.
Definition.
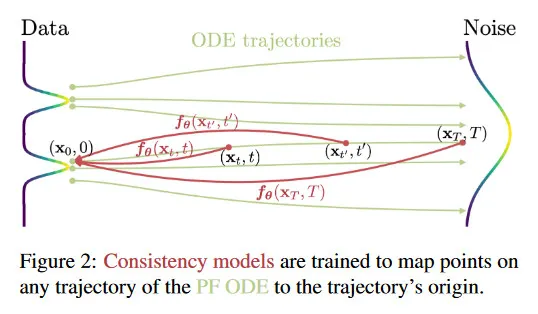
방정식 2에서 PF ODE의 해 궤적 {xt}t∈[0,T]\{\bold{x}_t\}_{t \in [0, T]}이 주어지면 consistency 함수를 f:(xt,t)↦xcf : (\bold{x}_t, t) \mapsto \bold{x}_c로 정의할 수 있다. consistency 함수는 self-consistency의 속성을 갖는다. 즉 동일한 PF ODE 궤적에 속하는 (xt,t)(\bold{x}_t, t)의 임의의 쌍에 대해 그 출력이 일관 된다. 모든 t,t′∈[ϵ,T]t, t' \in [\epsilon, T]에 대한 f(xt,t)=f(xt′,t′)f(\bold{x}_t,t) = f(\bold{x}_{t'}, t'). 그림 2 참조. consistency 모델 fθf_{\boldsymbol{\theta}}의 목표는 self-consistency 속성을 강제하는 학습으로 데이터에서 이 consistency 함수 ff를 추정하는 것이다. (상세한 내용은 섹션 4와 5 참조). 유사한 정의가 neural ODEs(Chen et al., 2018)의 맥락에서 neural flow(Bilos et al., 2021)에 대해 사용되었음에 참고하라. 그러나 neural flow와 달리 consistency 모델은 가역일 필요가 없다.
Parameterization.
임의의 consistency 함수 f(⋅,⋅)f(\cdot, \cdot)에 대해 f(xϵ,ϵ)=xϵf(\bold{x}_\epsilon, \epsilon) = \bold{x}_\epsilon가 성립한다. 즉 f(⋅,ϵ)f(\cdot, \epsilon)은 identity 함수이다. (여기서 ϵ\epsilon는 noise가 아니라 시간 축의 초기 시점을 말함) 이 제약조건을 boundary condition이라 부른다. 모든 consistency 모델은 이 boundary condition을 만족해야 하는데, 이는 consistency 모델의 성공적인 학습에서 결정적인 역할을 수행한다. 또한 이 boundary condition은 consistency 모델에 대한 가장 confining(제한적인) 아키텍쳐적 제약조건이다. 심층 신경망에 기반한 consistency 모델의 경우, 이 boundary condition을 거의 무료로 구현할 수 있는 2가지 방법을 논의한다. 출력의 차원이 x\bold{x}와 동일한 자유로운 형식의 심층 신경망 Fθ(x,t)F_{\boldsymbol{\theta}}(\bold{x},t)를 가졌다고 가정하자. 첫 번째 방법은 단순히 consistency 모델을 다음과 같이 파라미터화하는 것이다.
fθ(x,t)={xt=ϵFθ(x,t)t∈(ϵ,T](4)f_{\boldsymbol{\theta}}(\bold{x},t) = \begin{cases} \bold{x} & t = \epsilon \\ F_{\boldsymbol{\theta}}(\bold{x},t) & t \in (\epsilon, T] \end{cases} \tag{4}
두 번째 방법은 skip connection을 사용하여 consistency 모델을 파라미터화 하는 것이다. 즉
fθ(x,t)=cskip(t)x+cout(t)Fθ(x,t)(5)f_{\boldsymbol{\theta}}(\bold{x},t) = c_\text{skip}(t) \bold{x} + c_\text{out}(t)F_{\boldsymbol{\theta}}(\bold{x},t) \tag{5}
여기서 cskip(t)c_\text{skip}(t)와 cout(t)c_\text{out}(t)는 cskip(ϵ)=1c_\text{skip}(\epsilon) = 1이고 cskip(ϵ)=0c_\text{skip}(\epsilon) = 0와 같은 미분 가능한 함수이다. 이 방법으로 consistency 모델은 Fθ(x,t),cskip(t),cout(t)F_{\boldsymbol{\theta}}(\bold{x}, t), c_\text{skip}(t), c_\text{out}(t)가 모두 미분가능하면 t=ϵt = \epsilon에서 미분가능하다. 이것은 continuous-time consistency 모델을 학습하는 것에 결정적이다.(부록 B.1과 B.2). 방정식 5에서 파라미터화는 많은 성공적인 diffusion 모델(Karras et al 2022; Balaji et al., 2022)과 강한 유사성을 보이므로, consistency 모델을 구축하기 위해 강력한 diffusion 모델 아키텍쳐를 쉽게 빌려올 수 있다. 따라서 모든 실험에서 두 번째 파라미터화를 따른다.
Sampling.
잘 학습된 consistency 모델 fθ(⋅,⋅)f_{\boldsymbol{\theta}}(\cdot, \cdot)과 함께 초기 분포 x^T∼N(0,T2I)\hat{\bold{x}}_T \sim \mathcal{N}(\bold{0}, T^2\bold{I})에서 샘플링한 다음 x^ϵ=fθ(x^T,T)\hat{\bold{x}}_\epsilon = f_{\boldsymbol{\theta}}(\hat{\bold{x}}_T,T)에 대한 consistency 모델 평가로 샘플을 생성할 수 있다. 이것은 consistency 모델을 통한 하나의 forward pass만 필요하므로 single step로 샘플을 생성할 수 있다. 중요한 것은 denoising과 noise 삽입을 반복하여 consistency 모델을 여러 번 평가함으로써 샘플 품질 개선 할 수도 있다는 것이다. 알고리즘 1에서 요약한대로 이 multi-step 샘플링 절차를 통해 계산비용과 샘플 품질에 간의 유연한 tradeoff가 가능하다. 또한 zero-shot 데이터 편집에도 중요한 응용이 있다. 실제로 알고리즘 1의 {τ1,τ2,...,τN−1}\{ \tau_1, \tau_2, ..., \tau_{N-1}\} time points을 greedy 알고리즘을 사용하여 발견했는데, 여기서 time points은 ternary(삼진) 검색을 사용하여 알고리즘 1에서 얻어진 샘플들의 FID를 최적화하는 방식으로 한 번에 하나씩 pinpointed(지정) 된다. 이것은 prior time point가 주어지면 FID는 다음 time point의 unimodal 함수라는 가정을 한다. 우리의 실험적으로 이 가정이 성립함을 발견했고, 더 나은 탐색은 향후 과제로 남겨두었다.
Algorithm 1: Multistep Consistency Sampling
Input: Consistency model fθ(⋅,⋅)f_{\boldsymbol{\theta}}(\cdot, \cdot), time point의 시퀀스 τ1>τ2>...>τN−1\tau_1 > \tau_2 > ... > \tau_{N-1}, 초기 노이즈 x^T\hat{\bold{x}}_T
1.
x←fθ(x^T,T)\bold{x} \leftarrow f_{\boldsymbol{\theta}}(\hat{\bold{x}}_T, T)
2.
for n=1n = 1 to N−1N-1 do
a.
sample z∼N(0,I)\bold{z} \sim \mathcal{N}(\bold{0}, \bold{I})
b.
x^τn←x+τn2−ϵ2z\hat{\bold{x}}_{\tau_n} \leftarrow \bold{x} + \sqrt{\tau_n^2 - \epsilon^2}\bold{z}
c.
x←fθ(x^τn,τn)\bold{x} \leftarrow f_{\boldsymbol{\theta}}(\hat{\bold{x}}_{\tau_n}, \tau_n)
3.
output x\bold{x}
Zero-Shot Data Editing.
diffusion 모델과 유사하게 consistency 모델은 zero-shot에서 다양한 데이터 편집과 manipulation 응용을 허용한다. 이러한 작업을 수행하기 위한 명시적인 학습이 필요하지 않다. 예컨대 consistency 모델은 가우시안 노이즈 벡터에서 데이터 샘플로의 one-to-one 매핑을 정의한다. GANs이나 VAEs, normalizing flow 같은 latent 변수 모델과 유사하게 consistency 모델은 latent space(그림 11)을 traversing(가로지르며) 샘플 사이를 쉽게 보간할 수 있다. consistency 모델은 t∈[ϵ,T]t \in [\epsilon, T]에서 노이즈가 있는 임의의 noisy 입력 xt\bold{x}_t에서 xϵ\bold{x}_{\epsilon}을 복구하도록 학습되므로 다양한 노이즈 레벨에 대해 denoising을 수행할 수 있다(그림 12). 게다가 알고리즘 1의 multistep 생성 절차는 diffusion 모델의 iterative replacement 절차와 유사한 방식으로 zero-shot에서 특정 inverse 문제를 해결하는데 유용하다. 이를 통해 inpainting(그림 10), colorization(그림 8), super-resolution(그림 6b)와 SDEdit(Meng et al., 2021)의 stroke-guided image editing(그림 13) 등과 같은 이미지 편집의 맥락에서 많은 응용을 허용한다. 섹션 6.3에서 우리는 다양한 zero-shot 이미지 편집 작업에 대한 consistency 모델의 능력을 경험적으로 시연한다.

4 Training Consistency Models via Distillation

pre-trained score 모델 sϕ(x,t)s_{\boldsymbol{\phi}}(\bold{x},t)을 distilling 하는 것에 기반한 consistency 모델을 학습하는 첫 번째 방법을 제시한다. 우리의 논의는 score 모델 sϕ(x,t)s_{\boldsymbol{\phi}}(\bold{x},t)을 PF ODE로 연결하여 얻은 방정식 3의 경험적 PF ODE를 중심으로 한다. time horizon [ϵ,T][\epsilon, T]를 N−1N-1개의 부분 구간으로 이산화하여 t1=ϵ<t2<...<tN=Tt_1 = \epsilon < t_2 < ... < t_N = T의 boundary를 갖는 것을 고려하자. 실제로 우리는 Karras et al(2022)를 따라 ti=(ϵ1/ρ+(i−1)/(N−1)(T1/ρ−ϵ1/ρ))ρt_i = (\epsilon^{1/\rho} + (i-1)/(N-1)(T^{1/\rho}-\epsilon^{1/\rho}))^\rho의 공식을 사용하여 boundary를 결정한다(여기서 ρ=7\rho = 7). NN이 충분히 클 때, 수치적 ODE solver의 한 단계 이산화를 실행하여 xtn+1\bold{x}_{t_{n+1}}에서 xtn\bold{x}_{t_n}의 정확한 추정치를 얻을 수 있다. x^tnϕ\hat{\bold{x}}_{t_n}^{\boldsymbol{\phi}}라 표기되는 이 추정은 다음과 같이 정의된다.
x^tnϕ:=xtn+1+(tn−tn+1)Φ(xtn+1,tn+1;ϕ)(6)\hat{\bold{x}}_{t_n}^{\boldsymbol{\phi}} := \bold{x}_{t_{n+1}} + (t_n - t_{n+1})\Phi(\bold{x}_{t_{n+1}},t_{n+1};\boldsymbol{\phi}) \tag{6}
여기서 Φ(...;ϕ)\Phi(...;\boldsymbol{\phi})는 경험적 PF ODE에 적용된 한 단계 ODE solver의 업데이트 함수를 나타낸다. 예를 들어 Euler solver를 사용할 때 다음의 업데이트 규칙에 해당하는 Φ(x,t;ϕ)=tsϕ(x,t)\Phi(\bold{x},t;\boldsymbol{\phi}) = ts_{\boldsymbol{\phi}}(\bold{x},t)를 갖는다.
x^tnϕ:=xtn+1−(tn−tn+1)tn+1sϕ(xtn+1,tn+1)\hat{\bold{x}}_{t_n}^{\boldsymbol{\phi}} := \bold{x}_{t_{n+1}} -(t_n - t_{n+1})t_{n+1}s_{\boldsymbol{\phi}}(\bold{x}_{t_{n+1}},t_{n+1})
단순성을 위해 이 작업에서 한 단계 ODE solver만 고려한다. multi-step ODE solver로 일반화는 것은 간단하며 이것은 향후 작업으로 남겨둔다.
방정식 2의 PF ODE와 방정식 1의 SDE 사이의 연결 때문에(섹션 2), 우선 x∼pdata\bold{x} \sim p_\text{data}를 샘플링한 다음 x\bold{x}에 가우시안 노이즈를 추가하여 ODE 궤적의 분포를 따라 샘플할 수 있다. 구체적으로 데이터 포인트 x\bold{x}가 주어지면, 데이터셋에서 x\bold{x}를 샘플링하고, x\bold{x}를 이용해서 SDE N(x,tn+12I)\mathcal{N}(\bold{x}, t_{n+1}^2\bold{I})의 transition density에서 xtn+1\bold{x}_{t_{n+1}}을 샘플링한 다음, 방정식 6을 따라 xtn+1\bold{x}_{t_{n+1}}의 수치적 ODE solver의 이산화 한 단계를 사용하여 x^tnϕ\hat{\bold{x}}_{t_n}^{\boldsymbol{\phi}}를 계산하여 PF ODE 궤적 상의 인접한 데이터 포인트 쌍 (x^tnϕ,xtn+1)(\hat{\bold{x}}_{t_n}^{\boldsymbol{\phi}}, \bold{x}_{t_{n+1}})을 효율적으로 생성할 수 있다. 그 다음 쌍 (x^tnϕ,xtn+1)(\hat{\bold{x}}_{t_n}^{\boldsymbol{\phi}}, \bold{x}_{t_{n+1}})에 대한 출력 차이를 최소화여 consistency 모델을 학습 시킨다. 이를 통해 consistency 모델을 학습하기 위한 다음의 consistency distillation loss를 유도할 수 있다.
Definition 1.
consistency distillation loss는 다음과 같이 정의된다.
LCDN(θ,θ−;ϕ):=E[λ(tn)d(fθ(xtn+1,tn+1),fθ−(x^tnϕ,tn))](7)\mathcal{L}_\text{CD}^N(\boldsymbol{\theta}, \boldsymbol{\theta}^-;\boldsymbol{\phi}) := \mathbb{E}[\lambda(t_n)d(f_{\boldsymbol{\theta}}(\bold{x}_{t_{n+1}},t_{n+1}), f_{\boldsymbol{\theta}^-}(\hat{\bold{x}}_{t_n}^{\boldsymbol{\phi}},t_n))] \tag{7}
여기서 기대는 x∼pdata\bold{x} \sim p_\text{data}에 관해 취해지고 n∼U⟦1,N−1⟧n \sim \mathcal{U}\llbracket1, N-1 \rrbracket이고 xtn+1∼N(x;tn+12I)\bold{x}_{t_{n+1}} \sim \mathcal{N}(\bold{x}; t_{n+1}^2\bold{I})이다. 여기서 U⟦1,N−1⟧\mathcal{U}\llbracket1, N-1 \rrbracket는 {1,2,..,N−1}\{1,2,..,N-1\}에 대한 균등 분포를 표기한다. λ(⋅)∈R+\lambda(\cdot) \in \mathbb{R}^+은 positive weighting 함수이고, x^tnϕ\hat{\bold{x}}_{t_n}^{\boldsymbol{\phi}}는 방정식 6에 의해 주어진다. θ−\boldsymbol{\theta}^-는 최적화 과정에서 θ\boldsymbol{\theta}의 과거 값의 이동 평균을 나타내고 d(⋅,⋅)d(\cdot, \cdot)은 ∀x,y:d(x,y)⩾0\forall \bold{x}, \bold{y} : d(\bold{x}, \bold{y}) \geqslant 0이고 d(x,y)=0d(\bold{x}, \bold{y}) = 0이면 x=y\bold{x} = \bold{y}이고 iff을 만족하는 metric 함수이다.
달리 명시하지 않는 한, 이 논문에서 정의 1의 표기를 채택하고 E[⋅]\mathbb{E}[\cdot]을 모든 확률 변수에 대한 기대로 표기한다. 우리의 실험에서 ℓ2\ell_2 거리 d(x,y)=∥x−y∥22d(\bold{x}, \bold{y}) = \|\bold{x} - \bold{y}\|_2^2와 ℓ1\ell_1 거리 d(x,y)=∥x−y∥1d(\bold{x}, \bold{y}) = \|\bold{x} - \bold{y}\|_1과 Learned Perceptual Image Patch Similarity(LPIPS, Zhang et al(2018))을 고려한다. 모든 작업과 데이터셋에 걸쳐 λ(tn)≡1\lambda(t_n) \equiv 1이 가장 잘 수행한다는 것을 발견했다. 실제로 stochastic gradient descent로 모델 파라미터 θ\boldsymbol{\theta}에 대해 목적을 최소화하며 exponential moving average(EMA)를 사용하여 θ−\boldsymbol{\theta}^-를 업데이트 한다. 즉 decay rate 0⩽μ<10 \leqslant \mu < 1 일 때, 각 최적화 단계 이후에 다음 업데이트를 수행한다.
θ−←stopgrad(μθ−+(1−μ)θ)(8)\boldsymbol{\theta}^- \leftarrow \text{stopgrad}(\mu\boldsymbol{\theta}^- + (1-\mu)\boldsymbol{\theta}) \tag{8}
전체 학습 절차는 알고리즘 2에 요약되어 있다. deep reinforcement learning과 momentum based contrastive learning의 관례를 따라 fθ−f_{\boldsymbol{\theta}^-}를 target network로 fθf_{\boldsymbol{\theta}}를 online network로 사용한다. 간단하게 θ−=θ\boldsymbol{\theta}^- = \boldsymbol{\theta}를 설정하는 것과 비교하여 EMA 업데이트와 방정식 8의 stopgrad 연산이 학습 절차를 매우 안정화시키고 consistency 모델의 최종 성능을 개선하는 것을 발견했다.
Algorithm 2: Consistency Distillation (CD)
Input: 데이터셋 D\mathcal{D}, 초기 모델 파라미터 θ\boldsymbol{\theta}, learning rate η\eta, ODE solver Φ(⋅,⋅;ϕ),d(⋅,⋅),λ(⋅)\Phi(\cdot, \cdot;\boldsymbol{\phi}), d(\cdot, \cdot), \lambda(\cdot)과 μ\mu
1.
θ−←θ\boldsymbol{\theta}^- \leftarrow \boldsymbol{\theta}
2.
수렴할 때까지 반복
a.
x∼D\bold{x} \sim \mathcal{D}과 n∼U⟦1,N−1⟧n \sim \mathcal{U}\llbracket1, N-1\rrbracket 샘플
b.
xtn+1∼N(x;tn+12I)\bold{x}_{t_{n+1}} \sim \mathcal{N}(\bold{x};t_{n+1}^2 \bold{I}) 샘플
c.
x^tnϕ←xtn+1+(tn−tn+1)Φ(xtn+1,tn+1;ϕ)\hat{\bold{x}}_{t_n}^{\boldsymbol{\phi}} \leftarrow \bold{x}_{t_{n+1}} + (t_n - t_{n+1}) \Phi (\bold{x}_{t_{n+1}},t_{n+1};\boldsymbol{\phi})
d.
L(θ,θ−;ϕ)←λ(tn)d(fθ(xtn+1,tn+1),fθ−(x^tnϕ,tn))\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\theta}^-;\boldsymbol{\phi}) \leftarrow \lambda(t_n)d(f_{\boldsymbol{\theta}}(\bold{x}_{t_{n+1}}, t_{n+1}), f_{\boldsymbol{\theta}^-}(\hat{\bold{x}}_{t_n}^{\boldsymbol{\phi}},t_n))
e.
θ←−η∇θL(θ,θ−;ϕ)\boldsymbol{\theta} \leftarrow - \eta \nabla_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta}, \boldsymbol{\theta}^-;\boldsymbol{\phi})
f.
θ−←stopgrad(μθ−+(1−μ)θ)\boldsymbol{\theta}^- \leftarrow \text{stopgrad}(\mu\boldsymbol{\theta}^- + (1-\mu)\boldsymbol{\theta})
아래 asymptotic analysis에 기반하여 consistency distillation에 대한 이론적 정당화를 제시한다.
Theorem 1.
방정식 3의 경험적 PF ODE의 consistency 함수를 Δt:=max⁡n∈⟦1,N−1⟧{∣tn+1−tn∣}\Delta t := \max_{n \in \llbracket 1, N-1 \rrbracket} \{|t_{n+1} - t_n|\}와 f(⋅,⋅;ϕ)f(\cdot, \cdot;\boldsymbol{\phi}) 라고 하자. fθf_{\boldsymbol{\theta}}가 Lipschitz condition을 만족한다고 가정하면, 모든 t∈[ϵ,T] t \in [\epsilon, T]과 x\bold{x}와 y\bold{y}에 대해 ∥fθ(x,t)−fθ(y,t)∥2⩽L∥x−y∥2\|f_{\boldsymbol{\theta}}(\bold{x},t) - f_{\boldsymbol{\theta}}(\bold{y},t)\|_2 \leqslant L\|\bold{x}-\bold{y}\|_2를 만족하는 L>0L > 0이 존재한다. 또한 모든 n∈⟦1,N−1⟧n \in \llbracket1, N-1\rrbracket에 대해 tn+1t_{n+1}에서 호출된 ODE solver의 local error가 p⩾1p \geqslant 1일 때 O((tn+1−tn)p+1)O((t_{n+1} - t_n)^{p+1})로 uniformly bounded라고 가정하자. 그러면 LCDN(θ,θ;ϕ)=0\mathcal{L}_\text{CD}^N(\boldsymbol{\theta},\boldsymbol{\theta};\boldsymbol{\phi}) = 0이면 다음이 성립한다.
sup⁡n,x∥fθ(x,tn)−f(x,tn;ϕ)∥2=O((Δt)p)\sup_{n,\bold{x}}\|f_{\boldsymbol{\theta}}(\bold{x},t_n) - f(\bold{x},t_n;\boldsymbol{\phi})\|_2 = O((\Delta t)^p)
Proof.
증명은 귀납법을 기반으로 하며 수치적 ODE solver(Suli & Mayers, 2003)에 대한 global error bounds의 고전적인 증명과 유사하다. 전체 증명은 Appendix A.2 참조.
θ−\boldsymbol{\theta}^-가 θ\boldsymbol{\theta}의 기록의 실행 평균이기 때문에 알고리즘 2의 최적화가 수렴할 때 θ−=θ\boldsymbol{\theta}^- = \boldsymbol{\theta}가 성립한다. 즉 target과 online consistency 모델은 궁극적으로 서로 일치한다. 추가적으로 consistency 모델이 zero consistency distillation loss를 달성하면 Theorem 1에 의해 어떤 regularity 조건 아래 ODE solver의 step size가 충분히 작다면 추정된 consistency 모델이 arbitrarily(임의로) 정확해질 수 있다는 것을 암시한다. 중요한 것은 boundary 조건 fθ(x,ϵ)≡xf_{\boldsymbol{\theta}}(\bold{x}, \epsilon) \equiv \bold{x}가 consistency 모델 학습에서 자명한 해 fθ(x,t)≡0f_{\boldsymbol{\theta}}(\bold{x},t) \equiv \bold{0}가 발생하는 것을 precludes(배제하다)는 것이다.
θ−=θ\boldsymbol{\theta}^- = \boldsymbol{\theta} 또는 θ−=stopgrad(θ)\boldsymbol{\theta}^- = \text{stopgrad}(\boldsymbol{\theta})인 경우, consistency distillation loss LCDN(θ,θ−;ϕ)\mathcal{L}_\text{CD}^N(\boldsymbol{\theta},\boldsymbol{\theta}^-;\boldsymbol{\phi})를 무한히 많은 time step (N→∞)(N \to \infty)로 확장할 수 있다. 결과 continuous-time loss 함수는 NN이나 time step {t1,t2,...,tN}\{t_1, t_2,...,t_N\}을 지정할 필요가 없다. 그럼에도 불구하고 야코비안-벡터 곱이 포함되어 있어 효율적인 구현을 위해 forward-mode 자동 미분이 필요한데, 이것은 일부 딥러닝 프레임워크에서 잘 지원되지 않을 수 있다. 이 continuous-time distillation loss 함수를 Theorem 3에서 5까지 제공하고 상세한 내용은 부록 B.1에서 제공한다.

5 Training Consistency Models in Isolation

Consistency 모델은 어떤 pre-trained diffusion 모델에 의존하지 않고 학습될 수 있다. 이것은 기존의 diffusion diffusion distillation 기법과 다르며, consistency 모델을 생성 모델의 새로운 독립 계열로 만든다.
consistency distillation(CD)에서 pre-trained score 모델 sϕ(x,t)s_{\boldsymbol{\phi}}(\bold{x},t)에 의존하여 ground truth score 함수 ∇log⁡pt(x)\nabla \log p_t(\bold{x})를 근사한다. 결과적으로 다음의 비편향 추정기(부록 A의 Lemma 1)을 활용하여 이 pre-trained score 모델을 피할 수 있음이 밝혀졌다.
∇log⁡pt(xt)=−E[xt−xt2∣xt]\nabla\log p_t(\bold{x}_t) = -\mathbb{E}\Big[{\bold{x}_t - \bold{x} \over t^2}\Big| \bold{x}_t \Big]
여기서 x∼pdata\bold{x} \sim p_\text{data}이고 xt∼N(x;t2I)\bold{x}_t \sim \mathcal{N}(\bold{x};t^2\bold{I})이다. 즉 x\bold{x}와 xt\bold{x}_t가 주어지면 −(xt−x)/t2-(\bold{x}_t - \bold{x})/t^2을 사용하여 ∇log⁡pt(xt)\nabla \log p_t(\bold{x}_t)을 추정할 수 있다.
비편향 추정치는 N→∞N \to \infty의 극한에서 Euler 방법을 ODE solver로 사용할 때 consistency distillation(CD)에서 pre-trained diffusion 모델을 교체하는데 suffices(충분하다). 다음 결과에 의해 정당화된다.
Theorem 2.
Δt:=max⁡n∈⟦1,N−1⟧{∣tn+1−tn∣}\Delta t := \max_{n \in \llbracket 1, N-1 \rrbracket} \{|t_{n+1} - t_n|\}라 하자. dd와 fθ−f_{\boldsymbol{\theta}^-}가 모두 2번 연속 미분가능하고 bounded 2차 도함수를 가지며, 가중치 함수 λ(⋅)\lambda(\cdot)가 bounded이고 E[∥∇log⁡ptn(xtn)∥22]<∞\mathbb{E}[\|\nabla \log p_{t_n}(\bold{x}_{t_n})\|_2^2] < \infty이다. 또한 Euler ODE solver를 사용하고 pre-trained score 모델이 ground truth와 일치한다고 가정하자. 즉 ∀t∈[ϵ,T]:sϕ(x,t)≡∇log⁡pt(x)\forall t \in [\epsilon, T] : s_{\boldsymbol{\phi}}(\bold{x},t) \equiv \nabla \log p_t(\bold{x}). 그러면
LCDN(θ,θ−;ϕ)=LCTN(θ,θ−)+o(Δt)(9)\mathcal{L}_\text{CD}^N(\boldsymbol{\theta},\boldsymbol{\theta}^-;\boldsymbol{\phi}) = \mathcal{L}_\text{CT}^N(\boldsymbol{\theta},\boldsymbol{\theta}^-) + o(\Delta t) \tag{9}
여기서 기대는 x∼pdata\bold{x} \sim p_\text{data}에 관해 취해지고 n∼U⟦1,N−1⟧n \sim \mathcal{U}\llbracket1, N-1\rrbracket이고 xtn+1∼N(x;tn+12I)\bold{x}_{t_{n+1}} \sim \mathcal{N}(\bold{x};t_{n+1}^2\bold{I})이다. LCTN(θ,θ−)\mathcal{L}_\text{CT}^N(\boldsymbol{\theta},\boldsymbol{\theta}^-)라 표기되는 consistency training(CT) 목적은 다음과 같이 정의된다.
E[λ(tn)d(fθ(x+tn+1z,tn+1),fθ−(x+tnz,tn))](10)\mathbb{E}[\lambda(t_n)d(f_{\boldsymbol{\theta}}(\bold{x} + t_{n+1}\bold{z},t_{n+1}),f_{\boldsymbol{\theta}^-}(\bold{x} + t_n\bold{z}, t_n))] \tag{10}
여기서 z∼N(0,I)\bold{z} \sim \mathcal{N}(\bold{0}, \bold{I})이다. 또한 inf⁡NLCDN(θ,θ−;ϕ)>0\inf_N \mathcal{L}_\text{CD}^N(\boldsymbol{\theta},\boldsymbol{\theta}^-;\boldsymbol{\phi}) > 0이면 LCTN(θ,θ−)⩾O(Δt)\mathcal{L}_\text{CT}^N(\boldsymbol{\theta},\boldsymbol{\theta}^-) \geqslant O(\Delta t)이다.
Proof.
증명은 테일러 급수 전개와 score 함수(Lemma 1)의 속성에 기반한다. 전체 증명은 부록 A.3에 제공한다.
방정식 10을 consistency training(CT) loss라 부른다. 중요한 점은 L(θ,θ−)\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\theta}^-)이 online 네트워크 fθf_{\boldsymbol{\theta}}와 target 네트워크 fθ−f_{\boldsymbol{\theta}^-}에만 의존하며 diffusion 모델 파라미터 ϕ\boldsymbol{\phi}에 대해 완전히 agnostic(무지)하다는 것이다. loss 함수 L(θ,θ−)⩾O(Δt)\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\theta}^-) \geqslant O(\Delta t)는 나머지 o(Δt)o(\Delta t) 보다 느린 비율로 감쇠하므로 N→∞N \to \infty와 Δt→0\Delta t \to 0로 감에 따라 방정식 9의 loss를 지배하게 된다.
실용적인 성능을 개선하기 위해 학습하는 동안 스케쥴 함수 N(⋅)N(\cdot)에 따라 NN을 점진적으로 증가시키는 것을 제안한다. 직관적으로 (그림 3d) NN이 작을 때 (즉 Δt\Delta t이 클 때) consistency training(CT) loss가 기본 consistency distillation(CD) loss(즉 방정식 9의 좌변)에 대해 ‘variance’은 작지만 ‘bias’은 크므로 학습 초기에 더 빠르게 수렴을 facilitates(촉진하다). on the contrary(반대로) NN이 클 때(즉 Δt\Delta t이 작을 때) ‘분산’은 더 크지만 ‘편향’은 적어서 학습의 후반부에 바람직하다. 최고의 성능을 위해 μ\mu 또한 스케쥴 함수 μ(⋅)\mu(\cdot)에 따라 NN과 함께 변환해야 함을 발견했다. consistency training(CT)의 전체 알고리즘은 알고리즘 3에 제공되며 실험에서 사용한 스케쥴 함수는 부록 C에 주어진다.
Algorithm 3: Consistency Training(CT)
Input: 데이터셋 D\mathcal{D}, 초기 모델 파라미터 θ\boldsymbol{\theta}, learning rate η\eta, step schedule N(⋅)N(\cdot), EMA decay rate schedule μ(⋅)\mu(\cdot), d(⋅,⋅)d(\cdot, \cdot), λ(⋅)\lambda(\cdot)
1.
θ−←θ\boldsymbol{\theta}^- \leftarrow \boldsymbol{\theta}이고 k←0k \leftarrow 0
2.
수렴할 때까지 반복
a.
x∼D\bold{x} \sim \mathcal{D}과 n∼U⟦1,N(k)−1⟧n \sim \mathcal{U}\llbracket1, N(k)-1\rrbracket 샘플
b.
z∼N(0,I)\bold{z} \sim \mathcal{N}(\bold{0}, \bold{I}) 샘플
c.
L(θ,θ−)←λ(tn)d(fθ(x+tn+1z,tn+1),fθ−(x+tnz,tn))\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\theta}^-) \leftarrow \lambda(t_n)d(f_{\boldsymbol{\theta}}(\bold{x} + t_{n+1}\bold{z}, t_{n+1}), f_{\boldsymbol{\theta}^-}(\bold{x}+t_n\bold{z},t_n))
d.
θ←θ−η∇θL(θ,θ−)\boldsymbol{\theta} \leftarrow \boldsymbol{\theta} - \eta \nabla_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta}, \boldsymbol{\theta}^-)
e.
θ−←stopgrad(μ(k)θ−+(1−μ(k))θ)\boldsymbol{\theta}^- \leftarrow \text{stopgrad}(\mu(k)\boldsymbol{\theta}^- + (1-\mu(k))\boldsymbol{\theta})
f.
k←k+1k \leftarrow k+1
consistency distillation(CD)과 유사하게 θ−=stopgrad(θ)\boldsymbol{\theta}^- = \text{stopgrad}(\boldsymbol{\theta})일 때 consistency training(CT) loss LCTN(θ,θ−)\mathcal{L}_\text{CT}^N(\boldsymbol{\theta}, \boldsymbol{\theta}^-)는 Theorem 6에서 나타난대로 연속 시간(즉 N→∞N \to \infty)으로 확장될 수 있다. 이 연속 시간 loss 함수는 NN이나 μ\mu에 대한 스케쥴 함수가 필요 하지 않지만 효율적인 구현을 위해 forward-mode 자동 미분가 필요하다. 이산 시간 CT loss와 달리 Theorem 2에서 Δt→0\Delta t \to 0을 효과적으로 취하므로 연속 시간 목적과 함께 관련된 바람직하지 않은 ‘편향’이 없다. 더 상세한 내용은 부록 B.2에 relegate(귀속 시키다)

6 Experiments

우리는 consistency distillation과 consistency training을 활용하여 CIFAR-10, ImageNet 64x64, LSUN Bredroom 256x256과 LSUN Cat 256x256 등의 실제 이미지 데이터셋에 대해 consistency 모델을 학습한다. 결과는 Frechet Inception Distance(FID, 낮을 수록 좋음), Inception Score(IS, 높을수록 좋음), Precision(높을수록 좋음)과 Recall(높을수록 좋음)에 따라 비교된다. 추가적인 실험 상세는 부록 C 참조.

6.1 Training Consistency Models

consistency distillation(CD)와 consistency training(CT)에 의해 학습된 consistency 모델의 성능에 대한 다양한 하이퍼파라미터의 효과를 이해하기 위해 CIFAR-10에 대한 일련의 실험을 수행했다. 우선 CD에서 메트릭 함수 d(⋅,⋅)d(\cdot, \cdot), ODE solver, 이산화 단계 수 NN의 영향에 초점을 맞추고, 그 다음 CT에서 스케쥴 함수 N(⋅)N(\cdot)과 μ(⋅)\mu(\cdot)의 효과를 investigate(조사하다).
CD에 대한 실험을 설정하기 위해, 제곱 ℓ2\ell_2 거리 d(x,y)=∥x−y∥22d(\bold{x}, \bold{y}) = \|\bold{x}-\bold{y}\|_2^2, ℓ1\ell_1 거리 d(x,y)=∥x−y∥1d(\bold{x}, \bold{y}) = \|\bold{x}-\bold{y}\|_1와 Learned Perceptual Image Patch Similarity(LPIPS)를 metric 함수로 고려한다. ODE sovler에 대해 Karras et al(2022)에 자세히 설명된 Euler의 forward 방법과 Heun’s 2차 방법을 비교한다. 이산화 단계 수 NN에 대해 N∈{9,12,18,36,50,60,80,120}N \in \{9, 12, 18, 36, 50, 60, 80, 120 \}을 비교한다. 실험에서 CD로 학습된 모든 consistency 모델은 해당 pre-trained diffusion 모델로 초기화 되는 반면 CT로 학습된 모델은 무작위로 초기화된다.
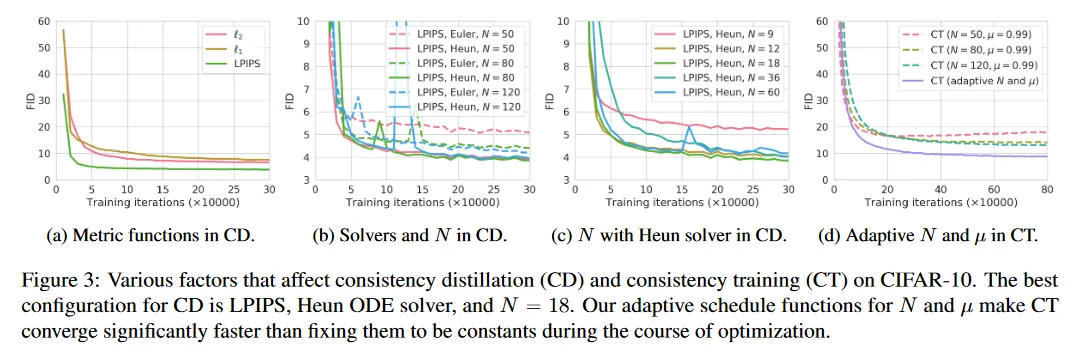
그림 3a에 나온 대로 CD에 대한 최적 메트릭은 LPIPS이다. 모든 학습 반복에 걸쳐 ℓ1\ell_1와 ℓ2\ell_2 보다 큰 폭 능가한다. 이것은 CIFAR-10에서 consistency 모델의 출력이 이미지이며, LPIPS가 자연 이미지 사이의 유사성을 측정을 위해 특별히 설계되었기 때문에 예상된 결과이다. 다음으로 CD에 가장 적합한 ODE solver와 이산화 단계 수 NN이 무엇인지 investigate(조사하다). 그림 3b와 3c에 보인대로 Heun ODE solver와 N=18N=18이 최고의 선택이다. 이는 diffusion 모델이 아니라 consistency 모델을 학습하는 것임에도 Karras et al(2022)의 추천과 일치한다(line). 게다가 그림 3b는 동일한 NN에 대해 Heun의 2차 solver가 Euler의 1차 sovler 보다 일관되게 능가함을 보인다. 이것은 고차 ODE solver에 의해 학습된 최적 consistency 모델이 동일한 NN에서 더 작은 추정 에러를 갖는다는 Theorm 1과 corroborates(부합하다). 그림 3c의 결과 또한 NN이 충분히 크면 CD의 성능이 NN에 insensitive(둔감하다)는 것을 보인다. 이러한 통찰을 바탕으로 별도의 언급이 없으면 이후 CD에 LPIPS와 Heun ODE solver를 사용한다. CD에서 NN은 CIFAR-10과 ImageNet 64x64에 대해 Karras et al(2022)의 제안을 따르며, 다른 데이터셋에 대해서는 별도로 조정한다. (자세한 내용은 부록 C 참조)
CD와 CT 사이의 강한 연관성 때문에 이 논문에서 CT 실험에서 throughout(내내) LPIPS를 채택했다. CD과 달리 CT에서 loss 함수가 특정 수치 ODE solver에 의존하지 않기 때문에 Heun의 2차 solver를 사용할 필요가 없다. 그림 3d에서 보이는 대로 CT의 수렴은 NN에 매우 민감하다. 작은 NN은 더 빠르게 수렴하지만 나쁜 샘플을 이끄는 반면 더 큰 NN은 느리게 수렴하지만, 수렴 시 샘플의 품질이 더 낫다. 이것은 섹션 5에서 분석와 일치하며, 수렴 속도와 샘플 품질 사이의 tradeoff에 균형을 잡기 위해 CT에서 NN과 μ\mu를 점진적으로 증가시키는 실용적 선택을 이끈다. 그림 3d에 보여진 대로 NN과 μ\mu의 적응형 스케쥴은 CT의 수렴 속도와 샘플 품질을 매우 개선한다. 우리 실험에서 다양한 해상도의 이미지에 대해 스케쥴 N(⋅)N(\cdot)과 μ(⋅)\mu(\cdot)을 별도로 조정했다. 자세한 내용은 부록 C 참조.

6.2 Few-Step Image Generation

Distillation.
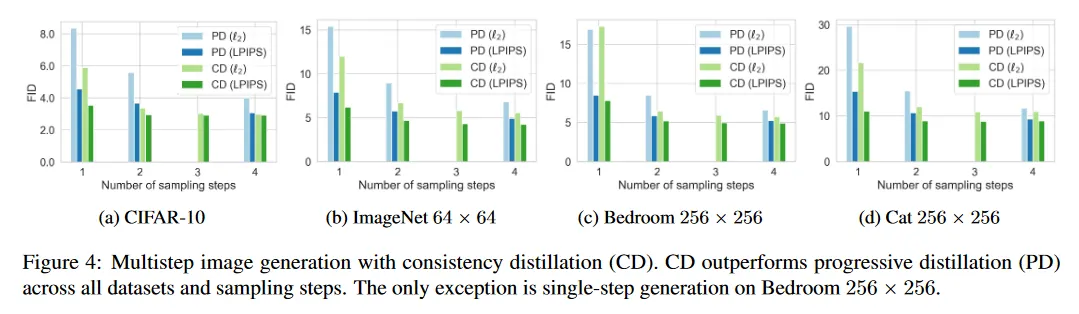
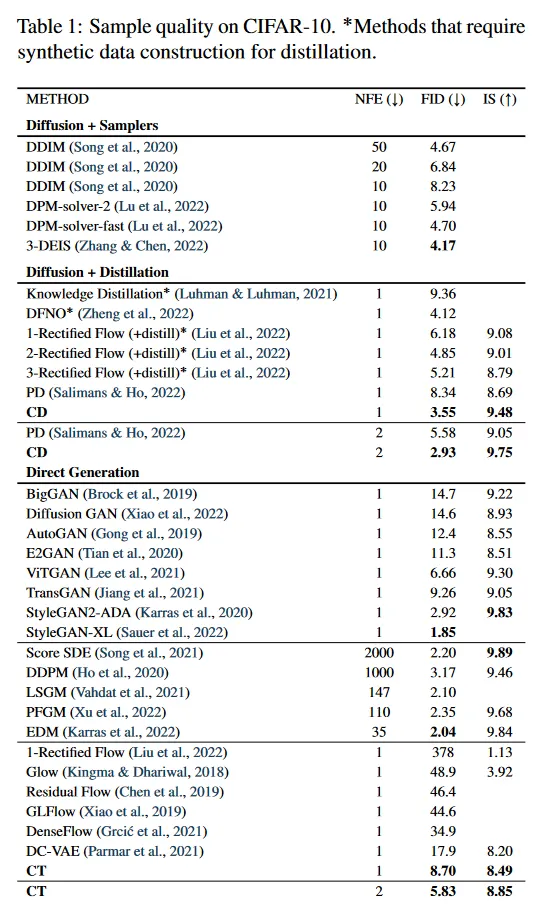
현재 문헌에서 우리의 consistency distillation(CD)과 가장 직접적으로 비교 가능한 접근은 progressive distillation(PD, Salimans & Ho(2022))이다. 둘 다 지금까지 distillation 이전에 합성 데이터를 구성하지 않는 유일한 distillation 접근이다. In stark contrast(극명한 대조를 이루며) knowledge distillation(Luhman 2021)과 DFNO(Zheng et al. 2022) 같은 다른 distillation 기법은 값비싼 수치적 ODE/SDE solver를 사용하여 diffusion 모델에서 numerous(수많은) 샘플을 생성하여 대규모 합성 데이터셋을 준비해야 한다. 우리는 CIFAR-10, ImageNet 64x64, LSUN 256x255에 대해 PD와 CD의 comprehensive(포괄적인) 비교를 수행한다. 결과는 그림 4 참조. 모든 방법은 in-house로 pre-trained 한 EDM 모델에서 distilling 된다. 원본 Salimans & Ho(2022) 논문의 제곱 ℓ2\ell_2 거리에 비해 LPIPS 거리를 사용하면 모든 샘플링 방법에서 PD가 일관되게 향상됨을 알 수 있다. PD와 CD 모두 더 많은 샘플링 단계를 취하면 더 개선된다. 우리는 Bedroom 256x256에서 단일 단계 생성의 경우 —ℓ2\ell_2를 사용한 CD가 ℓ2\ell_2를 사용한 PD에 약간 뒤쳐짐— 만 제외하고 모든 데이터셋, 샘플링 step, 메트릭 함수에 걸쳐 CD가 PD를 일관되게 능가함을 발견했다. 표 1에 보인대로 CD는 knowledge distillation(Luhman 2021)과 DFNO(Zheng et al. 2022) 같은 합성 데이터셋 구성을 필요로 하는 distillation 접근보다 뛰어난 성능을 보인다.
Direct Generation.
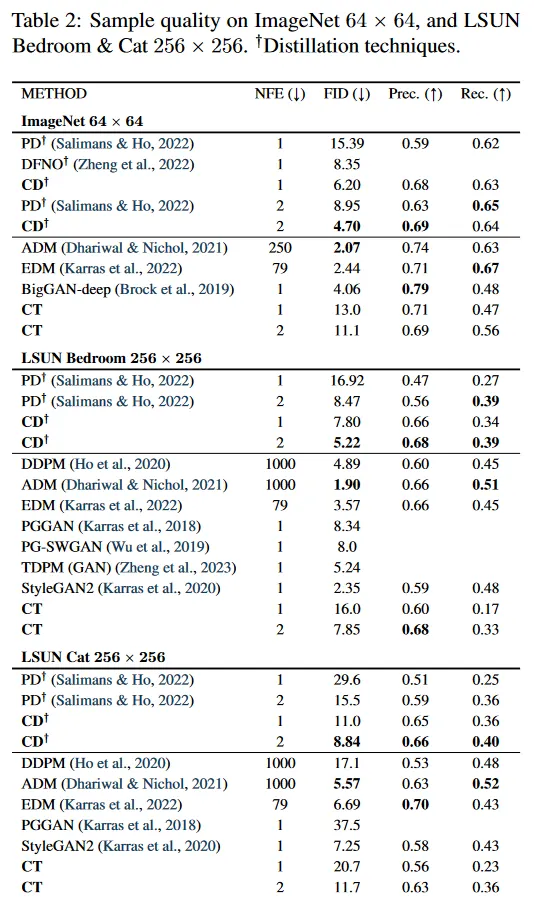
표 1과 2에서 one-step과 two-step 생성을 사용하여 consistency training(CT)의 샘플 품질을 다른 생성 모델과 비교한다. 참조를 위해 PD와 CD 결과도 포함한다. 두 표 모두 Salimans & Ho(2022)의 원본 논문에서 사용된 기본 설정인 ℓ2\ell_2 메트릭 함수에서 얻어진 PD 결과를 리포트한다. 공정한 비교를 위해 PD와 CD가 동일한 EDM 모델에서 distill 되도록 한다. 표 1과 2에서 CT가 CIFAR-10에서 기존의 single-step과 non-adversarial 생성 모델인 VAE와 normalizing flow을 큰 폭으로 능가함을 관찰할 수 있다. 게다가 CT는 distillation에 의존하지 않고도 PD의 one-step 샘플과 비교 가능한 품질을 달성한다. 그림 5에서 EDM 샘플(상단), single-step CT 샘플(중간), two-step CT 샘플(gkeks)에 제공한다. 부록 E에서 CD와 CT 모두에 대한 추가적인 샘플을 그림 14에서 21까지 보인다. 중요한 것은 동일한 초기 노이즈 벡터에서 얻은 모든 샘플이 CT와 EDM 모델이 서로 독립적으로 학습되었음에도 불구하고 상당한 구조적 유사성을 공유한다는 것이다. 이는 EDM과 달리 CT가 mode 붕괴에 덜 시달린다는 것을 나타낸다.

6.3 Zero-Shot Image Editing

diffusion 모델과 유사하게 consistency 모델은 알고리즘 1의 multi-step 샘플링 단계를 수정해서 zero-shot 이미지 편집을 허용한다. consistency distillation을 사용하여 LSUN bedroom 데이터셋에 학습된 consistency 모델을 사용하여 이 능력을 시연한다. 그림 6a 참조. 이런 consistency 모델이 colorization 작업에 학습된 적이 없음에도 테스트 시간에 gray-scale bedroom 이미지를 colorize 할 수 있음을 보인다. 그림 6b에서 동일한 consistency 모델이 저해상도 입력에서 고해상도 이미지를 생성할 수 있음을 보인다. 그림 6c에서 추가적으로 diffusion 모델의 SDEdit(Meng et al. 2021)과 같이 인간에 의해 생성된 stroke 입력에 기반하여 이미지를 생성할 수 있음을 보인다. 다시 한번, 이 편집 능력은 zero-shot으로 모델이 stroke 입력에 대해 학습된 적이 없다. 부록 D에서 inpainting(그림 10), 보간(그림 11), denoising(그림 12)에 대한 consistency 모델의 zero-shot 능력을 시연하며, colorization(그림 8), super-resolution(그림 9), stroke-guided 이미지 생성(그림 13)에 대한 더 많은 예시를 보인다.

7 Conclusion

consistency 모델에 대해 소개했다. 이것은 one-step과 few-step 생성을 지원하도록 특별히 설계된 생성 모델의 유형이다. 경험적으로 consistency distillation 방법이 여러 이미지 벤치마크와 작은 샘플링 반복에서 기존의 diffusion 모델에 대한 distillation 기법을 능가함을 보였다. 게다가 standalone 생성 모델로써 consistency 모델은 GAN을 제외하고 기존 single-step 생성 모델 보다 더 나은 샘플을 생성한다. diffusion 모델과 유사하게 inpainting, colorization, super-resolution, denoising, interpolation, stroke-guided iamge 생성 같은 zero-shot 이미지 편집 응용을 허용한다.
또한 consistency 모델은 deep Q-learning(Mnih et al., 2015)와 momentum-based contrastive learning(Grill et al., 2020) 등과 같은 다른 분야에서 사용된 기법과 striking(놀라운) 유사성을 공유한다. 이것은 이 다양한 영역 사이에 아이디어와 방법을 cross-pollination(전파)할 수 있는 흥미로운 prospect(전망)을 제공한다.
Made with