Abstract
우리는 self-supervised image representation learning에 대한 새로운 접근인 Bootstrap Your Own Latent(BYOL)을 소개한다. BYOL은 상호작용하며 학습하는 2개의 신경망, online과 target 네트워크에 의존한다. 이미지의 증강된 view에서, 우리는 online 네트워크를 동일한 이미지의 다르게 증강된 view 하에 target 네트워크 representation를 예측하도록 학습한다. 동시에 target 네트워크는 online 네트워크의 slow-moving average를 사용하여 업데이트한다. negative pair에 의존하는 최첨단 모델에 비해 BYOL은 그러한 것 없이 최첨단 성능을 달성했다. BYOL은 ResNet-50 아키텍쳐를 사용하여 ImageNet에서 linear evaluation으로 74.3%라는 top-1 분류 정확도와 더 큰 ResNet에서 79.6%의 정확도를 달성한다. 우리는 BYOL이 transfer와 semi-supervised 벤치마크 모두에서 현재 최첨단 성능과 동등하거나 더 낫다는 것을 보인다. 우리의 구현과 pre-trained 모델은 GitHub에 제공된다.
1 Introduction
좋은 이미지 representation을 학습하는 것은 computer vision에서 핵심 도전이다. 이는 downstream 작업에서 효율적인 학습을 가능하게 하기 때문이다. 이런 representation을 학습하기 위해 많은 다양한 학습 접근이 제안되었고 일반적으로 visual pretext 작업에 의존한다. 그들 사이에서 최첨단 contrastive 방법들은 동일한 이미지의 다양한 증강된 뷰(positive pair)의 representation 사이의 거리를 줄이고, 다른 이미지에서 증강된 뷰(negative pair)의 representation 사이의 거리를 증가시키도록 학습된다. 이러한 방법은 대형 배치 크기, memory bank 또는 커스터마이징된 mining 전략에 의존하여 negative pair를 조심스럽게 다뤄야 한다. 또한 이들의 성능은 이미지 증강의 선택에 결정적으로 의존한다.
이 논문에서 우리는 이미지 representation의 self-supervised learning을 위한 새로운 알고리즘인 Bootstrap Your Own Latent(BYOL)을 소개한다. BYOL은 negative pair 없이 최첨단 contrastive 방법보다 더 높은 성능을 달성한다. 이것은 네트워크의 출력을 반복적으로 bootstrap하여 향상된 representation의 목표로 사용한다. 게다가 BYOL은 contrastive 방법 보다 이미지 증강의 선택에 더 견고하다. 우리는 negative pair에 의존하지 않는 것이 이 개선된 견고성의 주요 원인 중 하나라고 추정한다. 이전의 bootstrapping에 기반한 방법들은 pseudo-label, cluster indices 또는 handful of label을 사용했지만, 우리는 representation을 직접적으로 bootstrap하는 방법을 제안한다. 특히 BYOL은 online과 target 네트워크라 불리는 2가지 신경망을 사용하여 서로 상호작용하며 학습한다. 이미지의 증강된 뷰에서 시작하여, BYOL은 online 네트워크가 동일한 이미지의 또 다른 증강된 뷰에 대한 target 네트워크의 representation를 예측하도록 학습한다. 이러한 모든 이미지에 대한 동일한 벡터를 출력하는 목적이 붕괴된 해를 허용하지만, 우리는 BYOL이 그러한 해에 수렴하지 않는다는 것을 실험적으로 보인다. 우리는 (i) online 네트워크에 predictor를 추가하고 (ii) online 파라미터의 slow-moving average를 target 네트워크로 사용하는 것이 online projection에 더 많은 정보를 인코딩하도록 장려하고 붕괴된 해를 피하도록 유도한다고 가설을 세운다.
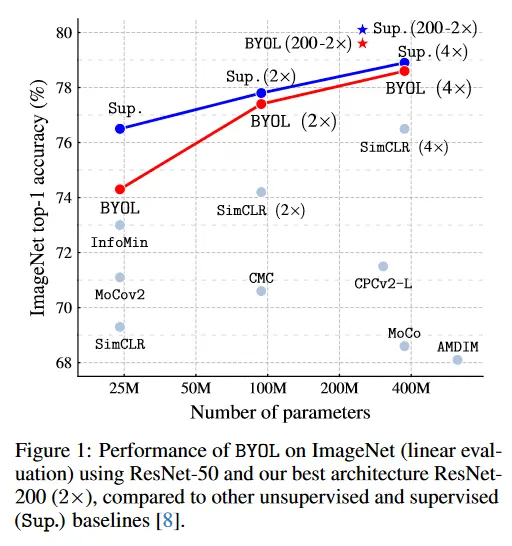
우리는 ResNet 아키텍쳐를 사용하여 BYOL이 학습한 representation을 ImageNet과 다른 vision 벤치마크에서 평가한다. ImageNet에서 linear 평가 프로토콜 하에 BYOL은 표준 ResNet-50에서 74.3%의 최상위 정확도, 더 큰 ResNet에서 79.6%의 최상위 정확도를 달성한다(그림 1). semi-supervised와 transfer 설정에서 우리는 현재 최첨단과 동등하거나 앞서는 결과를 얻는다. 우리의 기여는 다음과 같다. (i) negative pair를 사용하지 않고 ImageNet에서 linear evaluation 프로토콜 하에 최첨단 결과를 달성하는 self-supervised representation learning 방법인 BYOL을 소개한다(섹션 3). (ii) 학습된 representation이 semi-supervised와 transfer 벤치마크에서 최첨단을 능가하는 것을 보인다(섹션 4). (iii) BYOL이 contrastive 대응 모델과 비교하여 배치 크기와 이미지 증가의 집합의 변화에 더 강건함을 보인다(섹션 5). 특히 BYOL은 이미지 증강으로 random crop만 사용할 때, 강력한 contrastive baseline인 SimCLR 보다 훨씬 적은 성능 손실을 겪는다.
2 Related work
representation learning을 위한 대부분 unsupervised 방법은 generative 또는 discriminative로 구별할 수 있다. 생성적 접근은 데이터와 latent embedding에 대한 분포를 구축하고 학습된 embedding을 이미지 representation으로 사용한다. 이러한 접근의 대부분은 이미지의 auto-encoding 또는 adversarial learning에 의존하여 데이터와 representation을 함께 모델링한다. 생성적 방법은 일반적으로 픽셀 공간에서 직접 동작하지만 이것은 계산적으로 비싸고 이미지 생성을 위해 필요한 high level detail이 representation learning을 위해 불필요할 수 있다.
판별 방법 중에서 contrastive 방법은 현재 self-supervised learning에서 최첨단 성능을 달성한다. contrastive 접근은 동일한 이미지의 다른 뷰의 representation(positive pairs)을 가깝게 가져오고, 다른 이미지에서 뷰의 representation(negative pairs)을 멀리 떨어뜨려서 비용이 비싼 픽셀 공간에서의 생성 단계를 피한다. contrastive 방법은 각 예제를 많은 다른 여러 예제들과 비교해야 잘 작동하므로 negative 쌍을 사용하는 것이 필요한지에 대한 의문을 불러일으킨다.
DeepCluster[17]는 이 질문에 부분적으로 답한다. 이 방법은 이전 버전의 representation을 bootstrapping을 사용하여 다음 representation에 대한 target을 생성하고 데이터 포인트를 클러스터링하여 새로운 representation에 대한 classification target으로 각 샘플의 cluster index를 사용한다. 이는 negative 쌍의 사용을 피하지만 비용이 많이 드는 클러스터링 단계를 요구하고 자명한 해로 붕괴하는 것을 피하기 위해 특별한 조치를 필요로 한다.
일부 self-supervised 방법은 contrastive를 사용하지 않지만 representation을 학습하기 위해 보조의 수작업 예측 작업에 의존한다. 특히 relative patch prediction, colorizing gray-scale image, image in-painting, image jigsaw puzzle, image super-resolution, geometric transformation 등이 유용한 것으로 나타났다. 그러나 적절한 아키텍쳐를 사용하더라도, 이러한 방법은 contrastive 방법에 의해 성능이 앞지르고 있다.
우리의 접근은 강화학습(RL)을 위한 self-supervised representation learning 기법인 Prediction of Bootstrapped Latent(PBL, [49])와 유사한 점이 있다. PBL은 agent의 history representation과 미래 관찰의 encoding을 결합하여 학습한다. 관찰 인코딩은 에이전트의 representation을 학습하기 위한 taget으로 사용되고, 에이전트의 representation을 관찰 인코딩을 학습하는 target으로 사용된다. PBL과 달리 BYOL은 target를 제공하기 위해 slow-moving average를 사용하고, 두 번째 네트워크를 필요로 하지 않는다.
online network에 안정적인 target을 생성하기 위해 slow-moving average target network를 사용하는 것의 아이디어는 deep RL에서 영감 받았다. target network는 Bellman 방정식에 의해 제공된 bootstrapping 업데이트를 안정화하여 BYOL의 bootstrap 메커니즘을 안정화하는데 매력적인 방법이다. 대부분의 RL 방법이 고정된 target 네크워크를 사용하는 반면 BYOL은 target representation의 변화를 smoother 하기 위해 이전 네트워크의 weighted moving average를 사용한다.
semi-supervised 설정에서 unsupervised loss을 소수의 라벨에 대한 classification loss과 결합하여 학습을 안정화 한다. 이러한 방법 중 mean teacher(MT)는teacher라 불리는 slow-moving average 네트워크를 사용하여, student라 불리는 online network를 위한 target을 생성한다. teacher와 student 의 softmax 예측 사이의 일관성 loss이 classification loss에 추가된다. 반면 [20]은 semi-supervised learning 경우에서 MT의 효과성을 시연했다. 섹션 5에서 우리는 classification loss를 제거하면 유사한 접근이 붕괴되는 것을 보인다. 반면 BYOL은 online 네트워크의 위에 추가적인 predictor를 도입하여 붕괴를 방지한다.
마지막으로 self-supervised learning에서 MoCo는 slow-moving average network(momentum encoder)를 사용하여 memory bank에서 가져온 negative 쌍의 일관된 representation을 유지한다. 대신 BYOL은 bootstrap 단계를 안정화 하기 위한 수단으로 moving average network를 사용하여 prediction target을 생성한다. 우리는 섹션 5에서 이러한 안정화 효과가 기존 contrastive 방법들도 개선할 수 있음을 보인다.
3 Method
섹션 3.1에서 상세한 내용을 설명하기 전에 그 동기를 제기하는 것에서 시작한다. 많은 성공적인 self-supervised learning 접근은 [63]에서 도입된 cross-view prediction framework 위에 구축된다. 일반적으로 이러한 접근은 동일한 이미지의 서로 다른 뷰(예: 다양한 무작위 crop)를 예측하여 representation을 학습한다. 이런 접근은 예측 문제를 representation 공간에서 직접적으로 cast 한다. 이미지의 증강된 뷰의 representation이 동일한 이미지의 또 다른 증강된 뷰의 representation을 예측할 수 있어야 한다. 그러나 representation 공간에서 직접 예측하는 것은 붕괴된 representation을 이끈다. 예컨대 뷰에 걸쳐 일정한 representation은 항상 자기 자신을 완전히 예측할 수 있다. contrastive 방법은 예측 문제를 판별 문제로 재형식화 하여 해결한다. 증강된 뷰의 representation에서 다른 증강된 뷰의 representation과 다른 이미지의 증강된 뷰의 representation를 판별하도록 학습한다. 대부분의 경우에 이것은 붕괴된 representation을 찾는 것을 학습하는 것을 방지한다. 그러나 이러한 판별 접근은 일반적으로 각 증강된 뷰의 representation을 여러 negative 예제와 비교해야 하며, 이를 통해 판별 작업을 도전적으로 만드는 충분히 가까운 예제를 찾아야 한다. 이 작업에서 우리는 이러한 negative 예제가 붕괴를 방지하면서 높은 성능을 유지하는데 없어서는 안되는지 여부를 찾는 것을 목표로 했다.
붕괴를 막기 위한 간단한 솔루션은 고정된 무작위 초기화 네트워크를 사용하여 예측 target을 생성하는 것이다. 이것은 붕괴를 피하지만, 실험적으로 좋은 representation을 발생시키지 않는다. 그럼에도 불구하고 이 절차를 통해 얻어진 representation이 초기의 고정된 representation 보다 훨씬 낫다는 점은 흥미롭다. 우리의 ablation 연구(섹션 5)에서, 우리는 고정된 무작위 초기화된 네트워크를 예측함으로써 이 절차를 적용했고, ImageNet의 linear 평가 프로토콜에서 18.8% 최상위 정확도(Table 5a)를 달성했다. 반면 무작위로 초기화된 네트워크 만으로는 1.4%에 불과하다. 이 실험적 발견이 BYOL에 핵심 동기이다. target이 부르는 주어진 representation에서, online이라 부르는 새로운 잠재적으로 향상된 representation을 예측하여 학습할 수 있다. 그 후 이 절차를 반복하여 후속 online network를 추가 학습을 위한 새로운 target 네트워크로 사용하여 점점 더 높은 품질의 representation을 구축할 수 있을 것으로 기대할 수 있다. 실제로 BYOL은 이러한 bootstrapping 절차를 일반화하여 representation을 반복적으로 정제하지만, 고정된 체크 포인트 대신 online 네트워크의 slowly moving exponential average를 target 네트워크로 사용한다.
3.1 Description of BYOL
BYOL의 목표는 이후 downstream 작업을 위해 사용될 수 있는 representation 를 학습하는 것이다. 이전에 설명한 것과 같이 BYOL은 학습에 online과 target 네트워크라는 2개의 신경망을 사용한다. . online 네트워크는 가중치 의 집합으로 정의되고, encoder , projector , predictor 의 3개의 단계로 구성된다. 그림 2와 8 참조. target 네트워크는 online 네트워크와 동일한 아키텍쳐를 갖지만 다른 가중치 집합 를 사용한다. target 네트워크는 online network를 학습하기 위한 regression target을 제공하고 그것의 파라미터 는 online parameter 의 exponential moving average이다. 더 정확하게 target decay rate 이 주어지면, 각 학습 단계 이후에 우리는 다음의 업데이트를 수행한다.
이미지의 집합 와 에서 균등하게 샘플링된 이미지 , 2개의 이미지 증강 분포 와 가 주어지면, BYOL은 와 에 이미지 증강을 각각 적용하여 에서 두 개의 증강된 뷰 와 를 생성한다. . 처음 증강된 뷰 에서 online 네트워크는 representation 와 projection 를 출력한다. target 네트워크는 두 번째 증강된 뷰 에서 와 target projection 를 출력한다. 그 다음 에 대한 예측 를 출력하고 와 를 모두 와 로 -normalize 한다. 이 predictor는 오직 online branch에만 적용되므로 online과 target 파이프 라인 사이의 아키텍쳐는 비대칭이 된다. 마지막으로 normalized 예측과 target projection 사이의 mean squared error를 다음과 같이 정의한다.
방정식 2에서 loss 를 대칭으로 만들기 위해, 를 online network에, 를 target network에 각각 공급하여 를 계산한다. 각 학습 단계에서 우리는 stochastic 최적화를 수행하여 를 는 말고 에 대해서만 최소화한다. 그림 2에서 stop-gradient에 의해 나타난다. BYOL의 다이나믹스는 다음과 같이 요약된다.
여기서 optimizer는 optimizer이고 는 learning rate이다.
학습의 끝에서 우리는 [9]와 같이 encoder 만 유지한다. 다른 방법과 비교할 때, 우리는 최종 representation 에서 추론 시 가중치의 수만 고려한다. 전체 학습 절차는 부록 A 참조. JAX와 Haiku 라이브러리에 기반한 python pseudo-code는 부록 J 에서 제공된다.
3.2 Intuitions on BYOL’s behavior
BYOL이 을 에 대해 최적화하는 동안 붕괴를 방지하기 위한 명시적 항(negative 예제 같은)을 사용하지 않으므로, 에 관한 이 loss의 최소로 수렴할 것처럼 보일 수 있다.(예: 붕괴된 상수 representation). 그러나 BYOL의 target 파라미터 업데이트는 의 방향으로 이루어지지 않는다. 더 일반적으로 우리는 에 대해 BYOL의 다이나믹스가 어떤 loss 의 gradient descent라고 가정할 수 없다. 이것은 GAN과 유사하다. 여기서 discriminator와 generator 파라미터 모두에 관해 동시에 최소화되는 loss가 없다. 그러므로 BYOL의 파라미터가 의 최소로 수렴할 이유가 prior에 없다.
BYOL의 다이나믹스가 여전히 바람직하지 않은 평형 상태를 허용하지만, 우리의 실험에서 이런 평형 상태로 수렴하는 것을 관찰하지 못했다. 또한 BYOL의 predictor가 최적이라고 가정할 때, 즉
우리는 바람직하지 않은 평형 상태가 불안정할 것이라 가정한다. 실제로 이 최적 predictor 경우에 BYOL의 에 대한 업데이트는 기대적으로 기대 조건부 분산의 gradient를 따른다. (자세한 내용은 부록 H 참조)
여기서 는 의 -번째 feature
임의의 확률 변수 에 대하여 임에 유의하라. 를 target projection, 를 현재 online projection, 를 학습 다이나믹스의 stochasticities에 의해 online projection의 위에 도입된 추가 가변성이라 하자. online projection에서 정보를 순수하게 폐기하는 것은 조건부 분산을 감소시킬 수 없다.
특히 BYOL은 에서 상수 feature를 피한다. 임의의 상수 와 확률 변수 와 에 대해 이기 때문이다. 따라서 우리는 이러한 붕괴된 상수 평형 상태가 불안정하다고 가정한다. 흥미롭게도 에 관해 를 최소화하려고 하면, 상수 로 붕괴될 것이다. 대신 BYOL은 online projection이 포착한 가변성을 target projection으로 통합하여 를 에 더 가깝게 만든다.
게다가 online 파라미터 를 target 파라미터 로 hard-copy를 수행하는 것만으로도 새로운 가변성의 소스를 전파하는데 충분하다. 그러나 target 네트워크에서 갑작스런 변화는 최적 predictor의 가정을 깨뜨릴 수 있으며, 이 경우에 BYOL의 loss이 조건부 분산에 가까워지리라는 보장이 없다. 우리는 BYOL의 moving averaged target 네트워크의 주요 역할이 학습 중 predictor의 근접 최적성을 보장하는 것이라 가정한다. 이러한 해석의 실험적 근거는 섹션 5와 부록 I에서 제공한다.
3.3 Implementation details
Image augmentations
BYOL은 SimCLR[8]과 같은 이미지 증강의 집합을 사용한다. 우선 이미지에서 무작위 패치를 선택하고 이를 224x224로 resize하고 무작위 horizontal flip을 적용한다. 그 다음 color distortion이 적용되는데, brightness, contrast, saturation, hue adjustment와 option으로 grayscale conversion으로 구성된다. 마지막으로 가우시안 블러와 solarization이 패치에 적용된다. 이미지 증강에 대한 추가 세부사항은 부록 B 참조.
Architecture
우리는 기본 파라메트릭 encoder 와 로써 50개 레이어와 post-activation을 갖춘 convolutional residual network(ResNet-50(1x)v1)을 사용한다. 또한 [67, 48, 8]에서와 같이 더 깊고(50, 101, 152, 200 레이어) 더 넓은(1x에서 4x까지) ResNet을 사용한다. 구체적으로 representation 는 최종 average pooling 레이어의 출력에 해당하며, 이 레이어의 feature 차원은 2048이다(1x의 width인 경우). SimCLR에서와 같이 representation 는 MLP 에 의해 더 작은 공간으로 projected 되고 target projection 도 유사하다. 이 MLP는 출력 크기가 4096인 linear 레이어, batch normalization, ReLU와 256 차원 출력을 갖는 최종 linear 레이어로 구성된다. SimCLR과 달리, 이 MLP의 출력에는 bath normalized이 적용되지 않는다. predictor 는 와 동일한 아키텍쳐를 사용한다.
Optimization
우리는 LARS optimizer를 사용하며, 코사인 decay learning rate 스케쥴을 1000 epoch에 걸쳐 restart가 없이 적용하고 초기 10 epoch의 warm-up period를 갖는다. base learning rate를 로 설정하고 batch 크기에 따라 선형으로 스케일링한다(LearningRate = 0.2 x BatchSize / 256). 게다가 global weight decay 파라미터를 으로 설정하며, LARS 조정과 weight decay 모두에서 bias와 batch normalization을 제외한다. target 네트워크의 경우, exponential moving average 파라미터 는 에서 시작하여 학습하는 동안 1까지 증가된다. 구체적으로 로 설정한다. 여기서 는 현재 학습 단계이고 는 최대 학습 단계 수이다. 우리는 512개의 cloud TPU v3 코어에 대해 분산된 4096 배치 크기를 사용한다. 이 설정으로 ResNet-50(x1)에서 약 8시간 학습한다. 모든 하이퍼파라미터는 부록 J에 요약된다. 배치 크기가 512인 경우 추가 하이퍼파라미터 설정은 부록 G에서 제공된다.
4 Experimental evaluation
우리는 BYOL의 representaion의 성능을 ImageNet ILSVRC-2012 데이터셋 학습 집합에서 self-supervised pretraining 한 후에 평가한다. 우선 ImageNet(IN)에 대해 linear 평가와 semi-supervised 설정 성능을 평가한 다음, classification, segmentation, object detection과 depth estimation을 포함한 다른 데이터셋과 작업에서 전이 능력을 측정한다. 비교를 위해 ImageNet 학습 집합의 라벨을 사용하여 학습된 representation에 대한 점수도 리포트한다. 부록 E에서 Places365-Standard 데이터셋에서 pretraining representation을 사용하여 이 평가 프로토콜을 재현하여 BYOL의 일반화 능력을 평가한다.
Linear evaluation on ImageNet
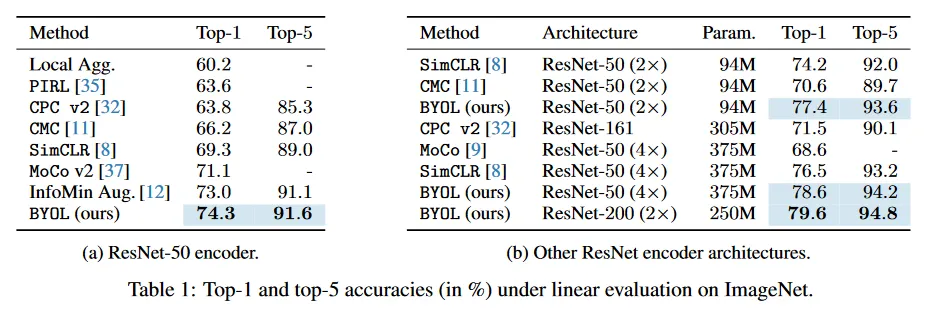
먼저 [48, 74, 41, 10, 8]과 부록 C.1에서 설명된 절차를 따라 frozen representation의 상단에 선형 classifier를 학습하여 BYOL의 representation을 평가한다. 우리는 Table 1에서 test set에서 top-1과 top-5 정확도를 %로 리포트한다. 표준 ResNet-50(x1)으로 BYOL은 74.3%의 top-1 정확도(91.6%의 top-5 정확도)를 달성했으며, 이는 이전 self-supervised 최첨단 보다 각각 1.3%(0.5%) 개선된 결과이다. 이것은 [8]의 supervised baseline인 76.5%와의 격차를 줄였지만, 여전히 더 강력한 [75]의 78.9% supervised baseline 아래에 놓인다. 더 깊고 더 넓은 아키텍쳐에서 BYOL은 일관되게 이전의 최첨단 성능을 능가하며(부록 C.2) 최고 79.6%의 top-1 정확도의 성능을 달성하여 이전의 self-supervised 접근보다 더 높은 랭킹을 기록했다. ResNet-50(4x)에서 BYOL은 78.6%을 달성했으며, 이는 동일한 아키텍쳐에 대한 [8]의 최고의 supervised baseline인 78.9%와 유사하다.
Semi-supervised training on ImageNet
다음으로 ImageNet의 train set의 작은 부분 집합을 사용하여 BYOL의 representation을 classification 작업에 fine-tuning 할 때의 성능을 평가한다. 이번에는 라벨 정보를 사용한다. 우리는 부록 C.1에서 자세히 설명한 [74, 76, 8, 32]의 semi-supervised 프로토콜을 따르고 [8]과 같은 ImageNet 라벨 학습 데이터의 1%와 10%의 고정된 분할을 사용한다. test set에서 top-1과 top-5 정확도를 Table 2에 리포트한다. BYOL은 다양한 아키텍쳐에서 일관적되게 이전 접근을 능가한다. 추가로 부록 C.1에서 자세히 설명된 대로 BYOL은 ImageNet 라벨의 100%를 사용하여 fine-tuning 할 때 ResNet-50으로 77.7%의 top-1 정확도를 달성한다.
Transfer to other classification tasks
우리는 ImageNet(IN)에 대해 학습된 feature가 일반적이고 여러 이미지 도메인에서 유용한지 또는 ImageNet 특화된 것인지 여부를 평가하기 위해 다른 classification 데이터셋에서 representation을 평가한다. 우리는 [8, 74]에서 사용된 동일한 classification 작업 집합에서 linear 평가와 fine-tuning을 수행하며 부록 D에 상세히 설명된 평가 프로토콜을 조심히 따른다. 성능은 각 벤치마크에 대한 표준 메트릭을 사용하여 리포트 되고 하이퍼파라미터 선택 후에 held-out test set에서 결과를 제공한다. linear 평가와 fine-tuning에 대한 결과는 Table 3에 리포트한다. BYOL은 모든 벤치마크에서 SimCLR을 능가하며, 12개 벤치마크 중 7개에서 supervised-IN baseline을 능가하고 나머지 5개의 벤치마크에서도 약간의 성능 차이만 보인다. BYOL의 representation은 CIFAR와 같은 작은 이미지, SUN397 또는 VOC2007와 같은 풍경, DTD와 같은 텍스쳐로 전이될 수 있다.
Transfer to other vision tasks
우리는 우리의 representation이 classification를 넘어 일반화되는지 평가하기 위해 semantic segmentation, object detection, depth estimation 등 computer vision 실무자에게 중요한 다양한 작업에서 평가한다.
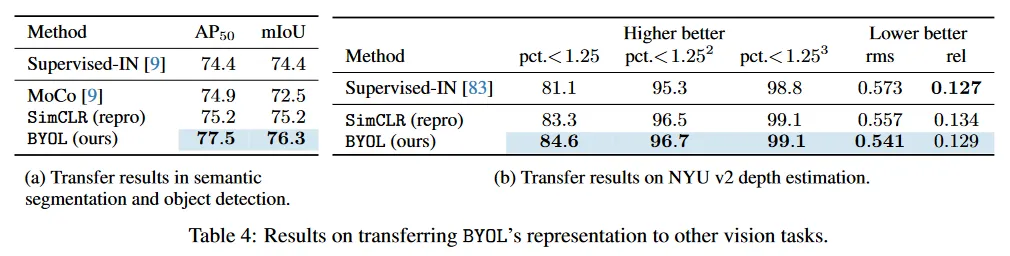
우선 부록 D.4에서 자세히 설명된 대로, VOC2012 semantic segmentation 작업에서 BYOL을 평가한다. 여기서 목표는 이미지에서 각 픽셀을 분류하는 것이다. 결과는 Table 4a에 리포트된다. BYOL은 supervised-IN baseline(+1.9 mIoU)와 SimCLR(+1.1 mIoU)를 모두 능가한다.
유사하게 우리는 Faster R-CNN 아키텍쳐를 사용하여 부록 D.5에 설명된 대로 object detection에서 평가를 수행하며, trainval2007에서 fine-tuning하고 test2007에서 표준 을 사용하여 결과를 리포트 한다. BYOL은 Supervised-IN baseline(+3.1 )과 SimCLR(+2.3 ) 보다 매우 낫다.
마지막으로 우리는 NYU v2 데이터셋에서 depth 추정을 평가한다. 여기서 단일 RGB 이미지가 주어질 때 장면의 depth map을 추정한다. Depth 예측은 네트워크가 geometry를 얼마나 잘 나타내느냐와 그 정보가 픽셀 정확도로 얼마나 잘 지역화 될 수 있느냐를 측정한다. 이 설정은 [83]에 기반하고 상세한 내용은 부록 D.6 참조. 우리는 일반적으로 사용되는 654개 이미지의 test 부분집합에서 평가하고 relative (rel) error, root mean squared (rms) error, percent of pixels(pct) 등 여러 일반적인 메트릭을 사용하여 결과를 Table 4b에 리포트 한다. 여기서 error 는 threshold 이하이고 여기서 는 예측된 dpeth이고, 는 ground truth depth이다. BYOL은 각 메트릭에 대해 다른 방법보다 우수하거나 동등한 성능을 보인다. 예컨대 chanllenging 측정치는 supervised와 SimCLR baseline과 비교하여 각각 점과 점 개선된다.
5 Building intuitions with ablations
우리는 BYOL의 동작과 성능의 직관을 제공하기 위해 ablation을 제시한다. 재현성을 위해 각 파라미터 설정을 3가지 seed로 실행하고 평균 성능을 리포트한다. 또한 성능 차이가 0.25보다 클 때, 최고와 최악 실행 사이의 절반 차이를 리포트한다. 이전 작업이 ablation을 100 epoch에서 수행했지만 우리는 100 epoch에서 상대적인 개선이 더 긴 학습 기간 동안 항상 유지되지 않는다는 점에 주목한다. 이러한 이유로, 우리는 64개 TPU v3 core에 대해 300 epoch에 대한 ablation을 실행하며 이것은 1000 epoch의 baseline 학습과 비교하여 일관성 있는 결과를 산출한다. 이 섹션에서 모든 실험에서 우리는 SimCLR과 같이 초기 learning rate를 0.3으로, 배치 크기를 4096, weight decay를 으로 설정한다. 기본 target decay rate 은 로 설정한다. 이 섹션에서는 부록 C.1에서 설명된 linear 평가 프로토콜하에 ImageNet에서 top-1 정확도로 결과를 리포트한다.
Batch size
contrastive 방법 중에서 미니배치에서 negative 예제를 뽑는 것들은 배치 크기가 줄어들 때 성능을 저하를 겪는다. BYOL은 negative 예제를 사용하지 않기 때문에, 더 작은 배치 크기에 더 견고할 것으로 기대한다. 이 가설을 실험적으로 검증하기 위해, 우리는 BYOL과 SimCLR을 각각 배치 크기를 128에서 4096까지 변화시키며 학습한다. 다른 하이퍼파라미터를 재조정하는 것을 피하기 위해, 우리는 배치 사이즈를 배 축소할 때 online 네트워크를 업데이트하기 전에 연이은 단계에 동안 gradient를 평균화한다. target 네트워크는 online 네트워크가 업데이트 이후에 매 단계마다 한 번 업데이트되며, 우리의 단계를 병렬로 누적한다.
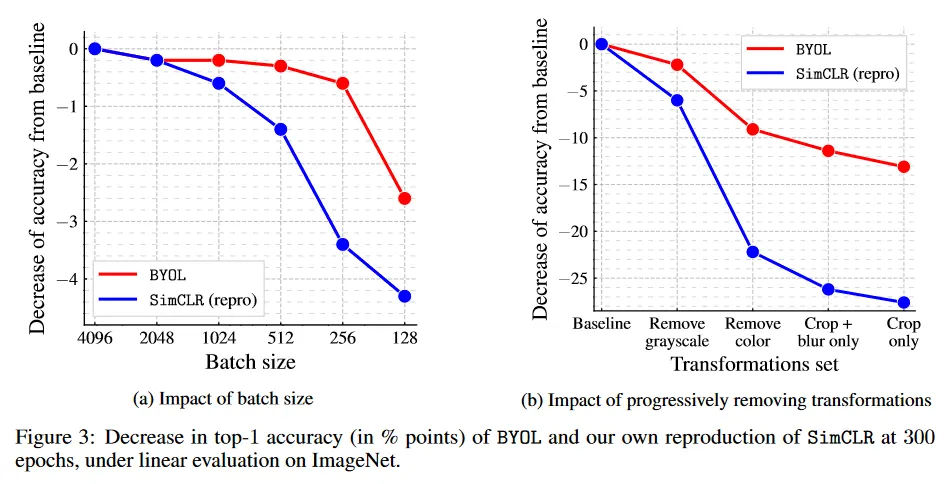
그림 3a에서 보이는대로 SimCLR의 성능은 배치크기와 함께 빠르게 악화되는데, 이는 negative 예제의 수가 감소했기 때문일 가능성이 높다. 반면에 BYOL의 성능은 배치 크기가 256에서 4096까지 넓은 범위에서 안정적으로 유지되며 encoder에서 batch normalization 레이어 때문에 더 작은 값에서만 성능이 떨어진다.
Image augmentations
contrastive 방법은 이미지 증강의 선택에 민감하다. 예컨대 SimCLR은 이미지 증강에서 color distortion을 제거하면 잘 동작하지 않는다. 이에 대한 설명으로, SimCLR은 동일한 이미지의 crop부분들이 대부분 color histogram을 공유하는 것으로 보인다. 동시에 color histogram은 이미지 별로 다르다. 그러므로 contrastive 작업은 이미지 증강으로써 무작위 crop만 사용할 경우 color histogram만 초점에 맞추어 대부분의 문제를 해결할 수 있다. 결과적으로 representation은 color histogram 이상의 정보를 유지하는 것에 인센티브가 없다. 이것을 방지하기 위해 SimCLR은 이미지 증강의 집합에 color distortion을 추가한다. 대신 BYOL은 online network가 target representation에 의해 포착된 임의의 정보를 유지하는데 인센티브를 제공하여 예측을 개선한다. 그러므로 동일한 이미지의 증강된 뷰가 동일한 color histogram을 공유하더라도 BYOL은 여전히 추가적인 feature를 representation에 유지하도록 인센티브를 받는다. 이러한 이유로, 우리는 BYOL이 contrastive 모델보다 이미지 증강의 선택에 더 견고하리라 믿는다.
그림 3b에 제시된 결과는 이러한 가설을 지지한다. 이미지 증강의 집합에서 color distortion을 제거할 때 BYOL의 성능은 SimCLR의 성능에 비해 덜 영향 받는다(BYOL에서는 -9.1점, SimCLR에서는 -22.2 점수). 증강이 단순히 무작위 crop으로 축소될 때도 BYOL은 여전히 좋은 성능을 보인다(59.4% 즉, 72.5%에서 -13.1점), 반면 SimCLR은 1/3 이상 나쁘다(40.3%, 즉 67.9%에서 -27.6점). 추가적인 ablation은 부록 F3에 리포트한다.
Bootstrapping
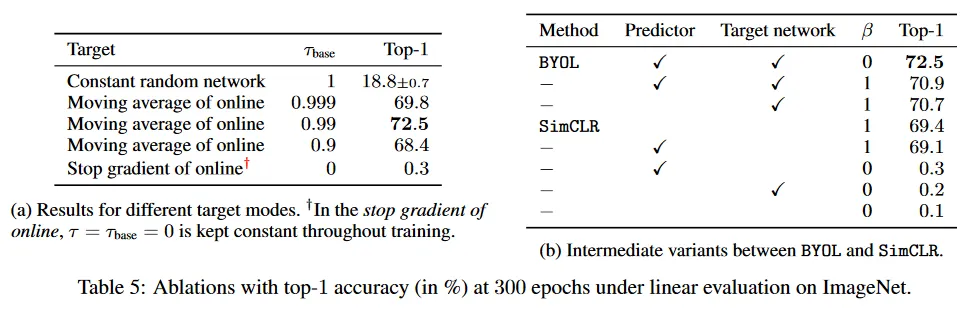
BYOL은 online network의 가중치의 지수 이동 평균을 사용하여 target 네트워크의 projected representation을 예측을 위한 target으로 사용한다. 이 방법에서 target 네트워크의 가중치는 online 네트워크의 가중치 보다 지연되고 더 안정적인 버전을 나타낸다. target decay rate가 1일 때, target 네트워크는 업데이트 되지 않고, 초기화에 해당하는 상수값으로 유지된다. target decay rate가 0인 경우, target network는 각 단계에서 online 네트워크로 즉시 업데이트된다. target이 너무 자주 업데이트하는 것과 너무 느리게 업데이트되는 것 사이의 trade-off가 존재한다. 이에 대해 Table 5a 참조. target network를 즉각적으로 업데이트하는 것()은 학습을 불안정하게 만들고, 빈곤한 성능을 산출한다. 반면 target을 업데이트하지 않는 것()은 학습을 안정적으로 만들지만 반복적인 개선을 방지하여 최종 representation의 품질이 낮아진다. decay rate이 0.9와 0.999 사이의 모든 값은 300 epoch에서 top-1 정확도 68.4% 이상의 성능을 산출한다.
Ablation to contrastive methods
이 하위 섹션에서 우리는 SimCLR과 BYOL을 동일한 형식화으로 재구성하여 BYOL이 SimCLR 보다 개선된 부분을 더 잘 이해하려 한다. InfoNCE 목적(부록 F.4)을 확장한 다음의 목적을 고려하자.
여기서 은 고정된 온도이고 은 가중치 계수이고, 는 배치 크기이고, 와 는 증강된 뷰의 배치이다. 여기서 각 배치 인덱스 에 대해 와 는 동일한 이미지에서 증강된 뷰이다. 실수값을 갖는 함수 는 증강된 뷰 사이의 쌍별 유사성을 정량화 한다. 임의의 증강된 뷰 에 대해 와 로 표기한다. 와 가 주어질 때, 우리는 normalized dot product를 고려한다.
사소한 세부사항까지(부록 F.5) (predictor 없음), (target 네트워크 없음)와 를 설정하면 SimCLR loss를 복구할 수 있다. predictor와 target 네트워크를 사용할 때, 즉 와 로 설정하고 일 때, BYOL loss를 복구한다. target 네트워크, predictor와 계수 의 영향을 평가하기 위해, 이것들에 대한 ablation을 수행한다. 결과는 Table 5b에 제시되며, 더 상세한 내용은 부록 F.4 참조.
negative 예제 없이(즉 ) 수행을 잘하는 변종은 bootstrap target network와 predictor를 모두 사용하는 BYOL 뿐이다. 온도 파라미터를 재조정하지 않고 BYOL의 loss에 negative 쌍을 추가하면 성능이 저하된다. 부록 F.4에서 온도를 적절히 조정하면 negative 쌍을 다시 추가하더라도 BYOL의 성능에 일치함을 보인다.
SimCLR에 간단히 target 네트워크를 추가하는 것만으로도 이미 성능이 개선된다(+1.6점). 이것은 MoCo에서 target 네트워크가 더 많은 negative 예제를 제공하기 위해 사용된 것에 대해 새로운 통찰을 제공한다. 여기서는 동일한 수의 negative 예제의 사용하는 경우에도 단순히 안정화 효과를 위해 target 네트워크는 사용하는 것이 유익하다는 것을 보인다. 마지막으로 predictor를 포함하도록 의 아키텍쳐를 수정하는 것이 SimCLR의 성능에 미미한 영향을 미친다는 것을 관찰했다.
Network hyperparameters
부록 F에서 다른 네트워크 파라미터들이 BYOL의 성능에 어떤 영향을 줄 수 있는 탐구한다. 여러 weight decay, learning rate과 projector/encoder 아키텍쳐를 반복적으로 실험하여, 작은 하이퍼파라미터를 변경이 최종 점수에 큰 영향을 미치지 않는다는 것을 관찰했다. 우리는 BYOL이나 SimCLR 모두에서 weight decay를 제거하면 네트워크가 발산하여, self-supervised 설정에서 weight regularization의 필요성을 강조한다. 또한 네트워크 초기화에서 scaling factor를 변경해도 성능에 영향을 주지 않는 것을 발견한다.(72% top-1 정확도 보다 높음)
Relationship with Mean Teacher
또 다른 semi-supervised 접근인 Mean Teacher(MT)는 적은 라벨에 대한 supervised loss를 추가적인 consistency loss과 결합한다. [20]에서 이 consistency loss가 student 네트워크의 logit과 teacher라 불리는 student 네트워크의 시간적으로 평균화된 버전 사이의 거리로 정의된다. BYOL에서 predictor를 제거하면 classification loss이 없는 MT의 unsupervised 버전이 되며, 원래의 아키텍쳐 노이즈(예: dropout) 대신 이미지 증강을 사용하게 된다. 그러나 BYOL의 변종은 붕괴하며(Table 5의 7행) 이것은 unsupervised 시나리오에서 추가적인 predictor가 붕괴를 방지하는데 핵심이라는 것을 시사한다.
Importance of a near-optimal predictor
Table 5b는 이미 predictor와 target 네트워크를 결합하는 것의 효과를 보인다. representation은 둘중 하나라도 제거될 때 붕괴한다. 우리는 추가로 최적에 가까운 predictor를 만들어서 target 네트워크를 제거하고도 붕괴를 방지할 수 있음을 발견한다. 이는 (i) 현재 배치에서 linear regression를 사용하여 최적의 linear predictor를 얻은 후 네트워크를 통해 에러를 역전파 하기(52.5% top-1 정확도), 또는 (ii) predictor의 learning rate를 증가시키는 것(66.5% top-1)으로 가능하다. 반면에 target network 없이 projector와 predictor learning rate를 모두 증가시키는 것은 빈곤한 결과를 산출한다(top-1에서 약 25%). 더 자세한 내용은 부록 I 참조. 이것은 predictor를 항상 최적에 가깝게 유지하는 것이 붕괴를 방지하는데 중요하다는 것을 나타낸다. 이것은 BYOL의 target 네트워크의 역할 중 하나이다.
6 Conclusion
우리는 image representation의 self-supervised learning을 위한 새로운 알고리즘인 BYOL을 소개한다. BYOL은 negative pair 없이 이전 버전의 출력을 예측하여 representation을 학습한다. 우리는 BYOL이 다양한 벤치마크에서 최첨단 결과를 달성함을 보인다. 특히 ResNet-50(1x)를 사용하여 ImageNet에서 linear 평가 프토토콜 하에 BYOL은 최첨단을 달성하고, self-supervised 방법과 [8]의 supervised learning baseline 사이의 대부분의 차이를 해소했다. ResNet-200(2x)를 사용하여 BYOL은 79.6%의 top-1 정확도를 달성한다. 이것은 이전의 최첨단 (76.8%)를 개선하면서도 30% 더 적은 파라미터를 사용한다.
그럼에도 불구하고 BYOL은 여전히 vision 응용에 특화된 기존 이미지 증강 집합에 의존한다. BYOL을 다른 모달(예: 오디오, 비디오, 텍스트 등)에 일반화하려면, 각각에 대해 적합한 유사한 증강 방법을 찾아야한다. 이러한 증강을 설계하는 것은 상당한 노력과 전문성을 필요로 한다. 그러므로 이러한 증강을 자동으로 탐색하는 것은 BYOL을 다른 모달로 일반화하는데 중요한 다음 단계가 될 것이다.
A Algorithm
Algorithm 1: BYOL: Bootstrap Your Own Latent
입력:
- 이미지 집합과 변환 분포
- 초기 online 파라미터, encoder, projector, predictor
- 초기 target 파라미터, target encoder, target projector
optimizer - optimizer, loss gradient를 사용하여 online 파라미터를 업데이트
- optimization step의 총 수와 배치 크기
- target network 업데이트 스케쥴과 learning rate 스케쥴
1.
for to do
a.
- 개 이미지의 샘플 배치
b.
for do
i.
- 이미지 변환 샘플링
ii.
and - projection 계산
iii.
and - target projection 계산
iv.
- 에 대한 loss 계산
c.
end
d.
- 에 관한 total loss gradient 계산
e.
- online 파라미터 업데이트
f.
- target 파라미터 업데이트
2.
end
출력: encoder
H Details on Equation 5 in Section 3.2
이 섹션에서 BYOL의 업데이트가 왜 섹션 3.2의 방정식 5와 관련되어 있는지 분명히 한다.
가 다음처럼 정의된다는 것을 떠올려라.
그리고 암시적으로 와 에 의존한다. 그러므로 단순히 라 표기하는 대신 라고 표기해야 한다. 단순성을 위해 임의의 파라미터 와 와 입력 에 대한 최적의 predictor 출력 를 라 표기한다.
BYOL은 방정식 5의 gradient를 따라 online 파라미터를 업데이트 하지만, 체인룰을 적용할 때 의 3번째 인수 에 관해 gradient만 고려한다. 이를 다시 작성하면
이 수량의 에 관한 gradient는 다음과 같다.
여기서 와 는 각각 첫 번째와 마지막 인수에 관한 의 gradient이다. envelope 정리를 사용하고 predictor의 최적성 조건 덕분에 항 이다. 그러므로 남은 항 은 gradient가 predictor의 입력을 통해서만 역전파된다. 이는 BYOL이 따르는 방향을 정확하게 일치한다.