프로그래밍/ 알고리즘의 복잡도

알고리즘의 복잡도

시간 복잡도

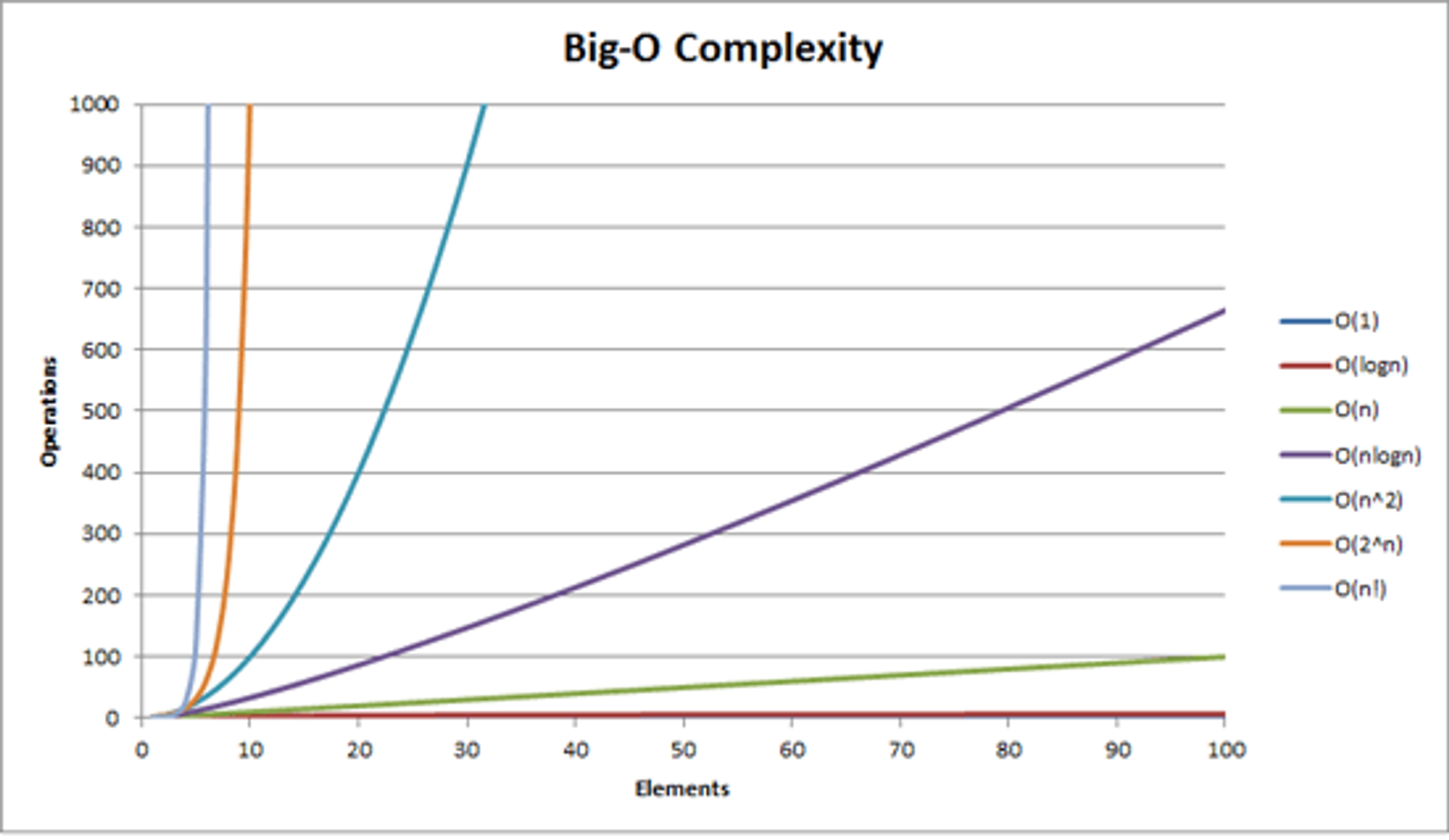
알고리즘의 수행 시간을 분석하는 것. 알고리즘을 구성하는 함수에 따른 수행 시간은 아래와 같다.

http://stackoverflow.com/questions/7830727/n-log-n-is-on

시간 복잡도의 표기는 여러개가 있지만, 기본적인 것 3개만 정리한다.

O (빅오)

알고리즘 시간의 하한선을 나타내는 표기법. 알고리즘 수행 시간이 아무리 빨라도 비교 함수에 비해 같거나 빠르다.

표기는 대문자 O 다음의 괄호안에 비교하는 함수를 넣는다. ex)

O(g(n)), O(n), O(n^{2}), O(\log n), O(n \log n)...

Ω (오메가)

알고리즘 시간의 상한선을 나타내는 표기법. 알고리즘 수행 시간이 아무리 빨라도 비교 함수에 비해 같거나 느리다.

표기는 Ω(오메가) 다음의 괄호안에 비교하는 함수를 넣는다. ex)

\Omega(g(n)), \Omega(n), \Omega(n^{2}), \Omega(\log n), \Omega(n \log n)...

Θ (세타)

알고리즘 시간의 상한-하한 범위선을 나타내는 표기법. 빅오와 오메가의 교집합을 의미한다.

\Theta(g(n)) = O(g(n)) \cap \Omega(g(n))

표기는 Θ(세타) 다음의 괄호안에 비교하는 함수를 넣는다. ex)

\Theta(g(n)), \Theta(n), \Theta(n^{2}), \Theta(\log n), \Theta(n \log n)...

공간 복잡도

알고리즘이 사용하는 메모리의 양을 분석하는 것.

알고리즘의 복잡도 분석

시간 복잡도 함수

시간 복잡도는 알고리즘의 절대적인 실행 시간을 나타내는 것이 아니라 알고리즘을 이루고 있는 연산들이 몇 번이나 실행되는지를 숫자로 표시한 것이다. 연산에는 산술 연산, 대입 연산, 비교 연산, 이동 연산 등이 포함되는데 복잡도 분석에서 이들 연산의 실행 횟수를 사용한다.

만일 동일한 조건에서 동일한 일을 하는데 알고리즘 A는 20번의 연산이 필요하고 알고리즘 B는 100번의 연산이 필요하다면 알고리즘 A가 더 효율적이라고 할 수 있다.

만일

n^{2}

을 구하는 문제에 대해 다음과 같은 알고리즘들이 있다면 각각의 실행 시간은 다음과 같다.

Show All

알고리즘

연산 횟수

sum = n*n

for i = 1 to n do sum = sum + n

2n

알고리즘 C

Open

for i = 1 to n do for j = 1 to n do sum = sum + 1

2n^{2}

엄밀하게 따지면 곱셈 연산이 덧셈 연산보다 수행 시간이 더 걸리지만 알고리즘 분석에서는 연산 횟수를 더 중요하게 보기 때문에 무시한다.