Search
Duplicate

AI/ f-divergence

ff-divergence

다음과 같이 정의되는 ff-divergence는 두 확률 분포를 밀도 비율의 측면에서 r(x)=p(x)/q(x)r(\bold{x}) = p(\bold{x})/q(\bold{x}) 비교한다. ff-divergence는 ϕ\phi-divergence라고도 불린다.
Df(p∥q)=∫q(x)f(p(x)q(x))dxD_f(p\|q) = \int q(\bold{x}) f \left({p(\bold{x}) \over q(\bold{x})} \right) d\bold{x}
여기서 f:R+→Rf : \mathbb{R}_+ \to \mathbb{R}은 f(1)=0f(1) = 0을 만족하는 볼록 함수이다. Jensen의 부등식로부터 Df(p∥q)≥0D_f(p\|q) \ge 0을 따르고 Df(p∥p)=0D_f(p\|p) =0이다. 따라서 DfD_f는 유효 다이버전스이다.

KL divergence

f(r)=rlog⁡(r)f(r) = r\log(r)를 사용해서 ff-divergence를 계산하면 Kullback-Leibler divergence가 된다.
DKL(p∥q)=∫p(x)log⁡p(x)q(x)dxD_{KL}(p\|q) = \int p(\bold{x}) \log {p(\bold{x}) \over q(\bold{x})} d\bold{x}

Alpha divergence

f(x)=41−α2(1−x1+α2)f(x) = {4 \over 1-\alpha^2}(1 - x^{{1+\alpha \over 2}})인 ff-divergence는 다음과 같은 alpha divergence가 된다. 여기서 α≠±1\alpha \ne \pm 1이다.
DαA(p∥q)≜41−α2(1−∫p(x)(1+α)/2q(x)(1−α)/2dx)D_\alpha^A(p\|q) \triangleq {4 \over 1-\alpha^2}\left(1 - \int p(\bold{x})^{(1+\alpha)/2} q(\bold{x})^{(1-\alpha)/2}d\bold{x} \right)
다른 일반적인 파라미터화는 다음과 같이 Minka가 사용한 것이다.
DαM(p∥q)=1α(1−α)(1−∫p(x)αq(x)1−αdx)D_\alpha^M(p\|q) = {1 \over \alpha(1-\alpha)}\left(1 - \int p(\bold{x})^\alpha q(\bold{x})^{1-\alpha}d\bold{x} \right)
이것은 Dα′A=DαMD_{\alpha'}^A = D_\alpha^M을 사용하여 Amari의 표기법으로 변환할 수 있다. 여기서 α′=2α−1\alpha' = 2\alpha-1
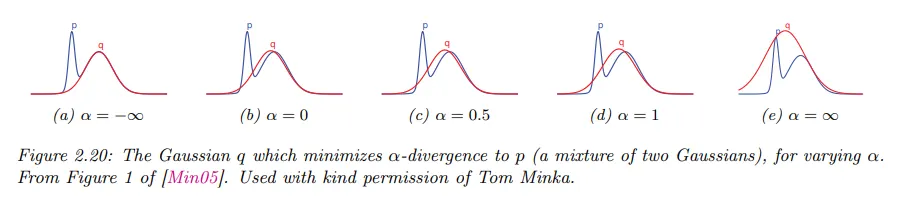
아래 그림에서 α→−∞\alpha \to -\infty에 따라 qq는 pp의 한 mode와 일치하는 것을 선호하는 반면, α→∞\alpha \to \infty이면 qq는 pp의 모든 부분을 커버하는 것을 선호한다는 것을 볼 수 있다. 더 정확하게 α→0\alpha \to 0이면 alpha divergence는 DKL(q∥p)D_{KL}(q\|p)가 되는 경향이 있고 α→1\alpha \to 1이 되면 alpha divergence는 DKL(p∥q)D_{KL}(p\|q)가 되는 경향이 있다. 또한 α=0.5\alpha=0.5에서 alpha divergence는 Hellinger 거리와 같아진다.

Hellinger distance

(squared) Hellinger distance는 다음과 같이 정의된다.
DH2(p∥q)≜12∫(p(x)12−q(x)12)2dx=1−∫p(x)q(x)dxD_H^2(p\|q) \triangleq {1\over2}\int\left(p(\bold{x})^{1\over2} - q(\bold{x})^{1\over2} \right)^2 d\bold{x} = 1 - \int \sqrt{p(\bold{x})q(\bold{x})}d\bold{x}
이것은 대칭이고 음이 아니고 삼각 부등식을 만족하기 때문에 유효한 거리 메트릭이다.
이것이 f(r)=(r−1)2f(r) = (\sqrt{r}-1)^2인 ff-divergence와 (상수 인자까지) 동등함을 볼 수 있다.
∫dx q(x)(p12(x)q12(x)−1)2=∫dx q(x)(p12(x)−q12(x)q12(x))2=∫dx(p12(x)−q12(x))2\begin{aligned} \int d\bold{x}\ q(\bold{x}) \left({p^{1\over2}(\bold{x}) \over q^{1\over2}(\bold{x})}-1 \right)^2 &= \int d\bold{x}\ q(\bold{x}) \left({p^{1\over2}(\bold{x}) - q^{1\over2}(\bold{x}) \over q^{1\over2}(\bold{x})}\right)^2 \\&= \int d\bold{x} \left(p^{1\over2}(\bold{x}) - q^{1\over2}(\bold{x}) \right)^2 \end{aligned}

Chi-squared distance

chi-squared distance χ2\chi^2은 다음처럼 정의된다.
χ2(p,q)≜12∫(q(x)−p(x))2q(x)dx\chi^2(p,q) \triangleq {1\over2}\int{(q(\bold{x})-p(\bold{x}))^2 \over q(\bold{x})}d\bold{x}
이것이 f(r)=(r−1)2f(r) = (r-1)^2인 ff-divergence와 (상수 인자까지) 동등함을 볼 수 있다.
∫dx q(x)(p(x)q(x)−1)2=∫dx q(x)(p(x)−q(x)q(x))2=∫dx1q(x)(p(x)−q(x))2\begin{aligned} \int d\bold{x}\ q(\bold{x}) \left({p(\bold{x}) \over q(\bold{x})}-1 \right)^2 &= \int d\bold{x}\ q(\bold{x}) \left({p(\bold{x}) - q(\bold{x}) \over q(\bold{x})}\right)^2 \\&= \int d\bold{x}{1 \over q(\bold{x})} \left(p(\bold{x}) - q(\bold{x}) \right)^2 \end{aligned}

참고

Made with