Search
Duplicate

Computer Vision/ 9. Optical and Scene Flow

web.stanford.edu
https://web.stanford.edu/class/cs231a/course_notes/09-optical-flow.pdf

1 Overview

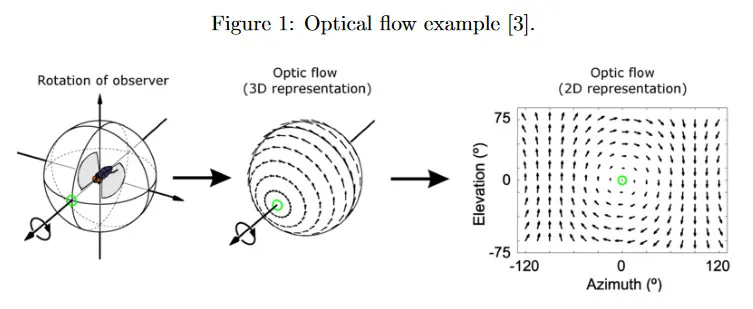
비디오가 주어지면 optical flow는 카메라(관찰자)와 장면(객체, surface, edges) 사이의 상대 움직임으로 인한 각 픽셀의 apparent(겉보기) 움직임을 설명하는 2d 벡터 장으로 정의된다. 카메라 또는 장면 또는 둘 다 움직일 수 있다. 그림 1은 반시계 방향으로 회전하는 파리를 보인다(파리의 시점에서). 장면이 정적이더라도 apparent 움직임의 2d optical flow는 원점을 중심으로 반대 방향(시계 방향) 의 회전을 나타낸다.

1.1 Motion field

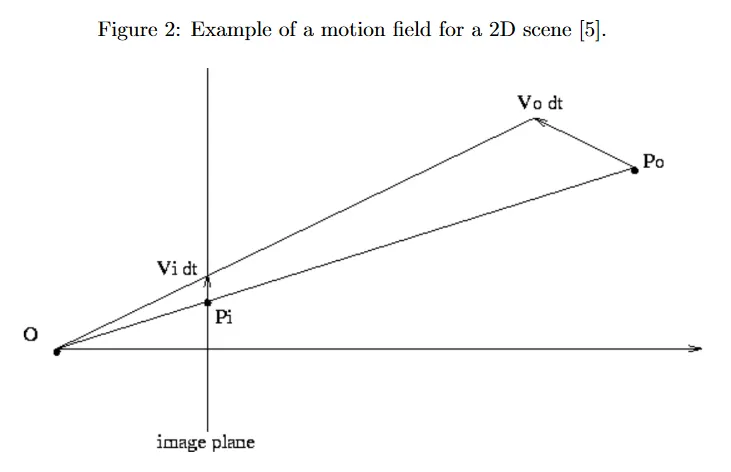
optical flow을 motion field와 혼동해서는 안된다. motion field는 관찰자의 이미지 평면에 대한 장면 내 점들의 3d motion vector를 설명하는 2d vector field를 의미한다. 그림 2는 간단한 2d 경우에서 motion field를 보인다(3d 장면을 top-down 관점에서 본다고 상상해 보라). 2d 객체 점 Po\bold{P}_o는 관찰자 OO가 보는 이미지 평면의 1d 점 Pi\bold{P}_i로 투영된다. 객체 점 Po\bold{P}_o가 Vo⋅dt\bold{V}_o \cdot dt(motion vector라 부른다)만큼 이동하면, 해당하는 투영된 1d 점은 Vi⋅dt\bold{V}_i \cdot dt 만큼 움직인다. 여기서 1d motion field는 이미지 평면에 위치한 모든 ii에 대한 모든 속도 값 Vi\bold{V}_i로 구성된다.
3d 장면을 일반화하여 픽셀 (x,y)(x, y)에 대한 motion field는 다음과 같이 주어진다.
(uv)=(dxdtdydt)=Mx′(1)\begin{pmatrix} u \\ v \end{pmatrix} = \begin{pmatrix} {dx \over dt} \\ {dy \over dt} \end{pmatrix} = \bold{Mx}' \tag{1}
여기서 x′=[dxdt,dydt,dzdt]⊤\bold{x}' = [{dx \over dt}, {dy \over dt}, {dz \over dt}]^\top는 3d 점의 motion을 나타내고 M∈R2×3\bold{M} \in \mathbb{R}^{2 \times 3}은 3d 점 위치 관점에 대한 픽셀 displacement(변위)의 편도함수를 포함한다.
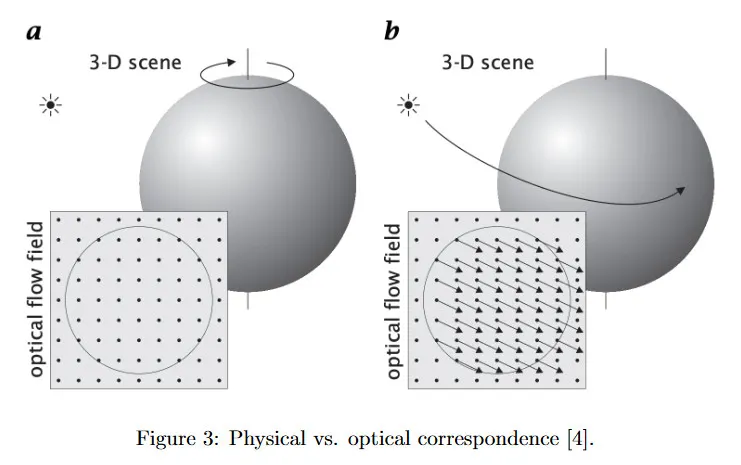
motion field는 이미지 평면에 투영된 3d motion의 이상적인 2d representation이다. 이것은 직접적으로 관찰할 수 없는 ‘ground truth’이고, 우리는 video와 같은 noisy 관찰에서만 optical flow(apparent motion)을 추정할 수 있다. optical flow는 항상 motion field와 동일하지 않다는 점이 중요하다. 예컨대 고정된 조명 소스를 갖고 균일하게 회전하는 구는 optical flow가 없지만 non-zero motion field를 갖는다. 반면 고정된 구에 조명이 그 주위를 움직이는 경우 non-zero optical flow이지만 zero motion field이다. 이 두 경우는 그림 3 참조.

2 Computing the optical flow

video를 시간에 걸쳐 포착된 프레임의 정렬된 시퀀스로 정의할 수 있다. 공간과 시간 모두의 함수인 I(x,y,t)I(x, y, t)는 시간 tt에서 프레임에서 픽셀 (x,y)(x, y)의 강도를 나타낸다. dense optical flow에서 각 시간 tt와 각 픽셀 (x,y)(x, y)에 대해 x-축과 y-축 모두에서 픽셀의 apparent 속도 u(x,y,t)=ΔxΔtu(x, y, t) = {\Delta x \over \Delta t}와 v(x,y,t)=ΔyΔtv(x, y, t) = {\Delta y \over \Delta t}를 각각 계산하기를 원한다. 각 픽셀에 대한 optical flow vector는 u=[u,v]⊤\bold{u} = [u, v]^\top로 주어진다.
이후 섹션에서 Lucas-Kanade 방법을 설명한다. 이것은 least-squares를 사용하여 u\bold{u}개의 서로 다른 픽셀 패치를 독립적으로 해결하기 위한 semi-local 접근을 사용한다.
brightness constancy assumption에서 우리는 동일 객체에 대한 이미지 평면에서 apparent 강도가 서로 다른 프레임에 걸쳐 변경되지 않는다고 가정할 수 있다. 이것은 시간 tt에서 t+Δtt + \Delta t 사이의 xx와 yy 방향에서 Δx\Delta x와 Δy\Delta y로 움직이는 픽셀에 대한 방정식 2에 의해 표현된다.
I(x,y,t)=I(x+Δx,y+Δy,t+Δt)(2)I(x,y,t) = I(x + \Delta x, y + \Delta y, t + \Delta t) \tag{2}
한가지 일반적인 단순화 방법은 Δt=1\Delta t = 1 (연속 프레임)을 사용하는 것이다. 이 경우 속도는 변위 u=Δxu = \Delta x와 v=Δyv = \Delta y에 동등하다. 그 다음 강의 슬라이드에서와 같이 I(x,y,t)=I(x+u,y+u,t+1)I(x, y, t) = I(x + u, y+u, t+1)을 얻을 수 있다.
다음으로 small motion assumption을 통해 프레임 간 움직임 (Δx,Δy)(\Delta x, \Delta y) —원문에는 (Δt,Δy)(\Delta t, \Delta y)로 나오는데 오타로 보임— 이 작다고 가정한다. 이를 통해 II를 1차 테일러 급수 전개를 사용하여 선형화 할 수 있다. 방정식 3에 의해 설명된다.
I(x+Δx,y+Δy,t+Δt)=I(x,y,t)+∂I∂xΔx+∂I∂yΔy+∂I∂tΔt+...≈I(x,y,t)+∂I∂xΔx+∂I∂yΔy+∂I∂tΔt(3)\begin{aligned} I(x + \Delta x,y + \Delta y, t + \Delta t) &= I(x, y, t) + {\partial I \over \partial x}\Delta x + {\partial I \over \partial y}\Delta y + {\partial I \over \partial t} \Delta t + ... \\ &\approx I(x, y, t) + {\partial I \over \partial x} \Delta x + {\partial I \over \partial y}\Delta y + {\partial I \over \partial t} \Delta t \end{aligned} \tag{3}
여기서 …는 테일러 급수 전개에서 고차 항을 나타내며 다음 줄에서 잘라낸다. 방정식 3에서 결과를 방정식 2로 교체하여 optical flow 제약 방정식에 도달한다.
0=∂I∂xΔx+∂I∂yΔy+∂I∂tΔt=∂I∂xΔxΔt+∂I∂yΔyΔt+∂I∂t=Ixu+Iyv+It(4)\begin{aligned} 0 &= {\partial I \over \partial x} \Delta x + {\partial I \over \partial y} \Delta y + {\partial I \over \partial t} \Delta t \\ &= {\partial I \over \partial x}{\Delta x \over \Delta t} + {\partial I \over \partial y}{\Delta y \over \Delta t} + {\partial I \over \partial t} \\ &= I_x u + I_y v + I_t \end{aligned} \tag{4}
Ix,Iy,ItI_x, I_y, I_t는 두 개의 공간 도함수와 시간 도함수의 축약할 수 있다.
−It=Ixu+Iyv=∇I⊤u=∇I⋅u⃗(5)\begin{aligned} -I_t &= I_xu + I_y v \\ &= \nabla I^\top \bold{u} \\ &= \nabla I \cdot \vec{\bold{u}} \end{aligned} \tag{5}
우리는 이것을 Ax=b\bold{Ax} = \bold{b} 형식의 선형 시스템으로 인식한다. ∇I=[Ix,Iy]⊤∈R2×1\nabla I = [I_x, I_y]^\top \in \mathbb{R}^{2\times 1}는 강도의 공간적 gradient를 나타내고 u⃗∈R2×1\vec{\bold{u}} \in \mathbb{R}^{2 \times 1}는 해결하기를 원하는 flow vector이다.
그러나 ∇I\nabla I가 fat maxtrix이기 때문에, 2개의 미지수 u,vu, v에 대한 단일 제약 방정식을 갖는 under-constrained 시스템이다. 이 제약은 우리에게 2개의 자유도에서 1개만 취한다. (u,v)(u,v) 해의 집합은 반드시 방정식 5에 의해 주어진 선을 따라 놓여야 한다. 그림 4 참조. 구체적으로 optical flow 제약은 u\bold{u}의 성분 중 공간적 gradient ∇I\nabla I의 방향을 따라 있는 normal flow만 제공할 수 있다. 그림 5는 예제 이미지의 xx와 yy 방향에서 공간적 이미지 gradient를 시각화한다. 높은 gradient 크기가 이미지의 edge에 해당하는 것을 볼 수 있다.
두 벡터 a\bold{a}와 b\bold{b} 사이의 dot product가 a⋅b=∥a∥∥b∥cos⁡(θ)\bold{a}\cdot \bold{b} = \|\bold{a}\|\|\bold{b}\| \cos(\theta)임을 떠올려라. 여기서 θ\theta는 두 벡터 사이의 각도이다. 그 다음 양변을 ∥b∥\|\bold{b}\|로 나누어 b\bold{b}에 대한 a\bold{a}의 projection을 얻을 수 있다. 그림 6 참조.
따라서 방정식 6은 optical flow 제약이 u\bold{u}를 ∇I\nabla I에 투영한 값을 제공하는 것을 보인다. 이것은 normal flow이다.
∇I∥∇I∥⋅u=−It∥∇I∥(6){\nabla I \over \|\nabla I\|} \cdot \bold{u} = {- I_t \over \| \nabla I\|} \tag{6}
그림 4는 u\bold{u}에 대한 해 공간을 그린다. 그러나 우리는 이 위에 이미지 공간도 시각화 할 수 있다. normal flow(해 공간)은 주어진 픽셀에서 이미지 강도의 spatial gradient 방향과 동일하다. 해 집합(선)은 spatial gradient에 대해 orthogonal이므로 이미지 공간에서 edge와 동일한 방향을 갖는다.
따라서 ∇I\nabla I 방향(normal flow)에서 u\bold{u}의 성분을 알지만, edge를 따라 u\bold{u}의 성분은 모른다. 이것은 해 집합으로 표현되며, 이 성분이 가질 수 있는 모든 가능한 값을 보인다.
u\bold{u}에 대한 가능한 값을 찾기 위해, 우선 normal flow의 크기와 동등한 거리만큼 spatial gradient 방향으로 이동한 다음, edge의 방향으로 임의의 (알 수 없는) 거리만큼 이동할 수 있다. 이것은 하나의 자유도를 나타낸다.
edge 방향에서 픽셀 움직임의 크기를 알수 없는 이슈는 ‘aperture problem’이라 한다. 그림 7 참조. 파란 사각형은 불투명이고 중앙에 작은 aperture를 형성하는 사각형 구멍이 있다. 밝은 회색 사각형은 움직이는 객체이다. 왼쪽에서 회색 사각형은 파란 사각형의 앞에 있다. 오른쪽에서 회색 사각형은 파란 사각형 뒤에 있다. 두 경우 모두 사각형은 아래와 오른쪽으로 동시에 움직인다. 빨간 화살표는 두 경우에서 인지된 움직임의 방향을 지시한다. 왼쪽 첫 번째 경우에서 사각형이 파란 사각형에 의해 블록되지 않으므로 우리는 실제 움직임의 방향을 인식할 수 있다. 그러나 오른쪽의 경우에 사각형은 파란 사각형 뒤에 있고 따라서 차폐 된다. 사각형의 움직임은 왼쪽과 오른쪽 동일한 방향이지만, 오른쪽으로의 움직임만 인지된다. 이는 이전에 도출한 내용과 일치한다. 우리는 사각형이 spatial gradient의 방향(여기서 x-축)으로 얼마나 움직였는지 알지만, 이미지 edge의 방향(여기서 y-축)에서 얼마나 움직였는지는 모른다.
이 문제를 완화하기 위해 spatial smoothness assumption을 사용할 수 있다. 이웃 점들은 장면에서 동일한 surface에 속하므로 동일한 optical flow u\bold{u}를 공유한다. 현재 픽셀 주위에 N×NN \times N 이웃을 정의하면, N2N^2 픽셀 각각에 대해 제약조건 ∇I(pi)⊤u=−It(pi)\nabla I(\bold{p}_i)^\top \bold{u} = -I_t(\bold{p}_i) 을 얻을 수 있다. 여기서 pi=[xi,yi]⊤p_i = [x_i, y_i]^\top은 ii-번째 픽셀의 위치이다. N2>2N^2 > 2를 가정하면 다음의 방정식 시스템을 가질 수 있다.
Au=b(Ix(p1)Iy(p1)⋮⋮Ix(pN2)Iy(pN2))(uv)=−(It(p1)⋮It(pN2))(7)\begin{aligned} \bold{Au} &= \bold{b} \\ \begin{pmatrix} I_x(\bold{p}_1) & I_y(\bold{p}_1) \\ \vdots & \vdots \\ I_x(\bold{p}_{N^2}) & I_y(\bold{p}_{N^2}) \end{pmatrix}\begin{pmatrix} u \\ v \end{pmatrix} &= - \begin{pmatrix} I_t(\bold{p}_1) \\ \vdots \\ I_t(\bold{p}_{N^2}) \end{pmatrix} \end{aligned} \tag{7}
그러면 방정식 7의 양변에 A⊤\bold{A}^\top을 곱하여 이 over-determined system의 least-suqares 해인 uls=(A⊤A)−1A⊤b\bold{u}_{ls} = (\bold{A}^\top\bold{A})^{-1}\bold{A}^\top\bold{b}를 찾기 위해 에러 ∥Au−b∥\|\bold{Au} - \bold{b}\|를 최소화한다. 다음의 normal equations을 검토하여 이 시스템의 해 가능성을 고려한다.
A⊤Au=A⊤b(∑Ix2∑IxIy∑IxIy∑Iy2)u=−(∑IxIt∑IyIt)(8)\begin{aligned} \bold{A}^\top\bold{Au} &= \bold{A}^\top\bold{b} \\ \begin{pmatrix} \sum I_x^2 & \sum I_x I_y \\ \sum I_x I_y & \sum I_y^2 \end{pmatrix}\bold{u} &= - \begin{pmatrix} \sum I_x I_t \\ \sum I_y I_t \end{pmatrix} \end{aligned} \tag{8}
합은 이웃 내 각 픽셀에 대해 이루어진다. 시스템이 해를 가지려면, A⊤A\bold{A}^\top \bold{A}가 noise의 존재로 인해 작지 않아야 한다. 예컨대 low-texture region은 작은 gradient 크기를 가지며, 이는 작은 eigenvalue와 쉽게 붕괴되는 u\bold{u} 값을 초래한다. 또한 A⊤A\bold{A}^\top \bold{A}는 잘 조건화되어야 하며, 이는 시스템이 측정된 에러에 견고해야 함을 의미한다. 왜냐하면 A⊤b\bold{A}^\top \bold{b}가 이미지 강도 데이터에서 계산된 모든 gradient에 의존하기 때문이다. 예컨대 edge에서 모든 큰 gradient는 동일한 방향을 가리키게 되어, 하나의 eigenvalue이 다른 것보다 훨씬 커지게 된다(큰 조건 수). u\bold{u}를 명확하게 해결할 수 있는 좋은 region은 방향적으로 다양한 spatial 구조를 가진 highly textured 영역이다. 이러한 영역에서는 다양한 방향으로 큰 gradient을 가지게 되어 잘 조건화된 A⊤A\bold{A}^\top \bold{A}를 얻는다.
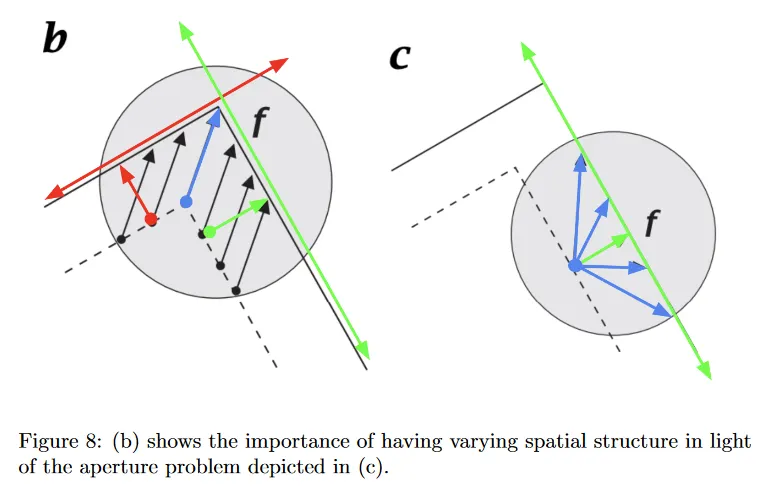
방향적으로 다양한 구조가 u\bold{u}를 해결하는데 어떻게 도움이 되는지 더 직관적으로 보기 위해 그림 8을 고려하자. 여기에 2가지 경우가 존재한다. 회색 원은 최적화하고 있는 픽셀 이웃을 나타낸다. 점선은 이전 time step의 객체를 나타내고, 실선은 현새 time step의 객체를 나타낸다. 이것은 객체의 실제 움직임을 묘사한다. (c)에서 aperture problem이 다시 발생하는 것을 볼 수 있다. 우리는 단일 normal flow vector(녹색)을 가지고 있어서 제약선(역시 녹색)을 따라 u\bold{u}에 대한 수많은 가능한 해(파란색)가 존재한다. 그러나 (b)에서 코너의 형태의 방향적으로 다양한 spatial 구조 가지고 있으며, 이는 서로 다른 방향의 두 edge로 볼 수 있다. 이제 두 개의 normal flow vector와 두 개의 제약 선(하나는 빨간색, 다른 하나는 녹색)을 갖는다. 두 제약선을 모두 만족하는 flow vector u\bold{u}에 대한 가능한 해가 하나만 존재하며 파란색으로 보여진다. 따라서 다양한 spatial 구조를 포함할 가능성을 높이기 위해 이웃 크기 NN을 늘리도록 유도된다. 그러나 이것에는 tradeoff가 있다. 다른 surface에 속하는 픽셀을 포함하기 위해 motion boundary를 넘을 수 있으며 따라서 u\bold{u}가 전체 이웃에 걸쳐 일정하지 않을 가능성이 점점 더 커진다.
실제로 전통적 공식의 Lucas-Kanade는 큰 camera motion, occlusion과 앞서 말한 가정의 집합의 위반으로 인해 견고하지 않다.
Made with