Search
Duplicate

AI/ Retrieval Augmented Generation(RAG)

Retrieval Augmented Generation(RAG)

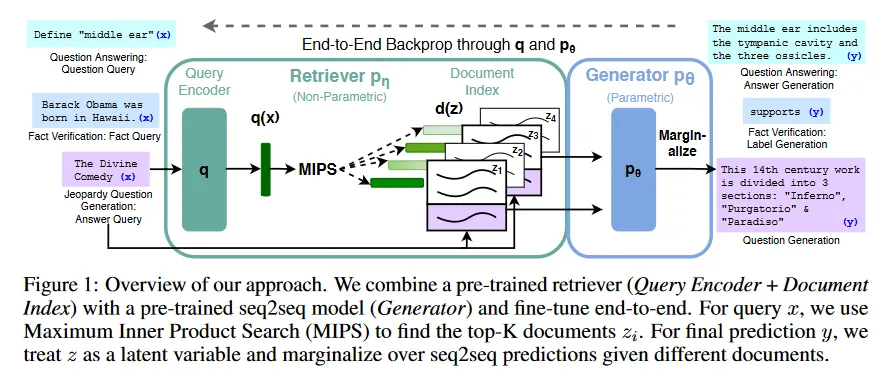
Retrieval Augmented Generation은 간단히 말해 LLM에 검색 기능을 붙인 형식이라 할 수 있다. 보다 구체적으로 전체 모델은 Retriever(검색기) pη(z∣x)p_\eta(z|x), Generator(생성기) pθ(yi∣x,z,y1:i−1)p_\theta(y_i|x, z,y_{1:i-1}), Vector DB로 구성되며, 사용자가 query를 날리면, 해당 query를 검색기를 이용하여 encoding한 후에, 그 결과를 이용하여 Vector DB에서 관련 있는 document를 검색하고, 해당 문서의 내용을 조건으로 Generator가 답변을 생성한다.
이러한 방식은 세상의 지식이 변경될 때마다 LLM을 업데이트할 필요 없이, Vector DB만 업데이트하면 항상 최신 정보를 업데이트 할 수 있다는 장점과 명확한 출처를 바탕으로 hallucination을 최소화할 수 있다는 장점이 있다. —일반적으로 hallucination은 모델이 잘 모르는 영역에 대해 답변할 때 주로 발생한다고 한다.

Model

RAG 논문의 저자들은 RAG를 2가지 방식으로 시도했는데, 하나는 RAG-Sequence Model이고, 다른 하나는 RAG-Token Model이다.
RAG-Sequence 모델은 검색된 상위 kk개 문서별로 전체 시퀀스를 생성한 후에 최종적으로 그 결과를 합하는 방식이다. 이는 다음 형식으로 정의된다. (여기서 pη(z∣x)p_\eta(z|x)는 검색기이고 pθ(yi∣x,z,y1:i−1)p_\theta(y_i|x, z,y_{1:i-1})는 생성기)
pRAG-Sequence(y∣x)≈∑z∈top-k(p(⋅∣x))pη(z∣x)pθ(y∣x,z)=∑z∈top-k(p(⋅∣x))pη(z∣x)∏iNpθ(yi∣x,z,y1:i−1)\begin{aligned} p_\text{RAG-Sequence}(y|x) &\approx \sum_{z \in \text{top-k}(p(\cdot|x))} p_\eta(z|x)p_\theta(y|x,z) \\&= \sum_{z \in \text{top-k}(p(\cdot|x))} p_\eta(z|x)\prod_i^N p_\theta(y_i|x,z,y_{1:i-1}) \end{aligned}
RAG-Token 모델은 검색된 상위 kk개 문서에 대해 각 토큰을 생성할 때마다 각기 다른 문서를 참고하여 전체 시퀀스를 생성하는 방식이다. 이는 다음의 형식으로 정의된다.
pRAG-Token(y∣x)≈∏iN∑z∈top-k(p(⋅∣x))pη(z∣x)pθ(yi∣x,z,y1:i−1)p_\text{RAG-Token}(y|x) \approx \prod_i^N \sum_{z\in\text{top-k}(p(\cdot|x))} p_\eta(z|x)p_\theta(y_i|x,z,y_{1:i-1})
RAG-Sequence는 각 문서별로 시퀀스를 생성한 후에 결과를 합치므로, 한 번만 시퀀스를 생성하는 RAG-Token에 비해 계산 효율성이 떨어지지만, RAG-Sequence는 각 문서에 독립적인 시퀀스를 생성하기 때문에 더 높은 품질을 갖는다.

Retriever

RAG의 검색기 pη(z∣x)p_\eta(z|x)는 Dense Passage Retriever(DPR)에 기반한다. bi-encoder 아키텍쳐를 따르는 DPR은 query와 document를 각각 임베딩하여 텍스트 검색을 수행한다. RAG에서 임베딩에는 BERT를 사용하여 검색기를 다음과 같이 정의한다.
pη(z∣x)∝exp⁡(d(z)⊤q(x))d(z)=BERTd(z)q(x)=BERTq(x)\begin{aligned} p_\eta(z|x) &\propto \exp(\bold{d}(z)^\top\bold{q}(x)) \\ \bold{d}(z) &= \text{BERT}_d(z) \\ \bold{q}(x) &= \text{BERT}_q(x) \end{aligned}
여기서 d(z)\bold{d}(z)는 BERTBASE\text{BERT}_\text{BASE} document encoder에 의해 생성된 문서의 dense 표현이고, q(x)\bold{q}(x)는 또한 BERTBASE\text{BERT}_\text{BASE}에 기반한 query encoder에 의해 생성된 query 표현이다.
top-k(pη(⋅∣x))\text{top-k}(p_\eta(\cdot|x)), 즉 prior 확률 pη(z∣x)p_\eta(z|x)가 가장 높은 kk개 문서 zz의 목록을 계산하는 것은 Maximum Inner Product Search(MIPS) 문제이다. MIPS는 대규모 데이터베이스에서 특정 쿼리 벡터와 가장 높은 내적(inner product)를 갖는 벡터를 찾는 문제로 추천 시스템이나 정보 검색, 컴퓨터 비전, 기계 학습 등에서 중요하게 사용된다. 고차원 공간에서 정확한 내적 계산을 하는 것은 큰 비용이 들지만, 효율적인 근사 방법을 사용하여 sub-linear 시간에서 해결될 수 있다.
RAG에서는 pre-trained bi-encoder를 사용하여 검색기를 초기화하고 document index를 구축한다. RAG에 이러한 document index를 non-parametric memory라 부른다. RAG를 최신 지식으로 업데이트 하는 것은 바로 이 document index를 업데이트하여 가능하다.

Generator

생성기 pθ(yi∣x,z,y1:i−1)p_\theta(y_i|x,z,y_{1:i-1})는 임의의 encoder-decoder를 사용하여 모델링 될 수 있다. RAG 논문 저자들은 BART를 사용했다.
RAG에서 생성기 파라미터 θ\theta를 parametric memory라고 부른다.

Training

RAG의 학습은 직접적인 supervision 없이 검색기와 생성기를 결합 한 후 입력-출력 쌍 (xj,yj)(x_j, y_j)을 이용하여 target의 negative marginal log-likelihood ∑j−log⁡p(yj∣xj)\sum_j -\log p(y_j|x_j)를 최소화하는 형태로 이루어진다.
학습하는 동안 document encoder BERTd\text{BERT}_\text{d}를 업데이트하는 것은 document index를 주기적으로 업데이트 해야 하므로 비용이 많이 든다. RAG 논문 저자들은 이 단계가 강력한 성능에 필수적이지 않다고 판단해서 document encoder와 index를 고정하고 query encoder BERTq\text{BERT}_\text{q}와 BART\text{BART} 생성기만 fine-tuning했다.

Decoding

테스트 시간에 arg max⁡yp(y∣x)\argmax_y p(y|x)를 근사하기 위해 RAG-Sequence와 RAG-Token은 다른 방법을 사용한다.
RAG-Token 모델은 전이 확률을 갖는 표준 auto-regressive seq2seq 생성기로 pθ′(yi∣x,y1:i−1)=∑z∈top-k(p(⋅∣x))pη(zi∣x)pθ(yi∣x,zi,y1:i−1)p_\theta'(y_i|x,y_{1:i-1}) = \sum_{z\in\text{top-k}(p(\cdot|x))} p_\eta(z_i|x)p_\theta(y_i|x,z_i,y_{1:i-1})를 디코딩하기 위해 pθ′(yi∣x,y1:i−1)p_\theta'(y_i|x, y_{1:i-1})을 표준 beam decoder에 연결할 수 있다.
RAG-Sequence는 likelihood p(y∣x)p(y|x)를 전통적인 토큰별 likelihood로 분해할 수 없기 때문에 단일 beam search로 해결할 수 없고, 대신 각 문서 zz에 대해 beam search를 실행하고 pθ(yi∣x,z,y1:i−1)p_\theta(y_i|x,z,y_{1:i-1})를 사용하여 각 가설에 점수를 매긴다. 이렇게 하면 모든 문서의 beam에서 나타나지 않을 수 있는 가설의 집합 YY가 생성되고, 가설 yy의 확률을 추정하기 위해 yy가 beam에 나타나지 않는 각 문서 zz에 대해 추가적인 forward pass를 실행하고, 생성기 확률에 pη(z∣x)p_\eta(z|x)를 곱한 다음 marginal를 위해 beam 전체에 걸쳐 확률을 합산한다. 논문 저자들은 이 방법은 ‘Thorough Decoding’이라 부른다.
Thorough Decoding은 출력 시퀀스가 길어지면 ∣Y∣|Y|가 커져 많은 forward pass가 필요하기 때문에 더 효율적인 decoding을 위해 yy가 x,zix, z_i에서 beam search 동안 생성되지 않는 경우 pθ(y∣x,zi)≈0p_\theta(y|x,z_i) \approx 0라는 추가 근사를 만들 수 있다. 이렇게 하면 후보 집합 YY가 생성된 후 추가적인 forward pass를 실행할 필요가 없다. 저자들은 이 절차를 ‘Fast Decoding’이라 부른다.

참고

Made with