Search
Duplicate

AI/ Article/ Flow-based Deep Generative Models

Flow-based Deep Generative Models
So far, I’ve written about two types of generative models, GAN and VAE. Neither of them explicitly learns the probability density function of real data, $p(\mathbf{x})$ (where $\mathbf{x} \in \mathcal{D}$) — because it is really hard! Taking the generative model with latent variables as an example, $p(\mathbf{x}) = \int p(\mathbf{x}\vert\mathbf{z})p(\mathbf{z})d\mathbf{z}$ can hardly be calculated as it is intractable to go through all possible values of the latent code $\mathbf{z}$.
https://lilianweng.github.io/posts/2018-10-13-flow-models/
지금까지 작성한 생성 모델 GAN과 VAE는 모두 실제 데이터 p(x) (x∈D)p(\bold{x}) \ (\bold{x} \in \mathcal{D})의 확률 밀도 함수를 명시적으로 학습할 수 없었다. 왜냐하면 매우 어렵기 때문이다. p(x)=∫p(x∣z)p(z)dzp(\bold{x}) = \int p(\bold{x}|\bold{z})p(\bold{z})d\bold{z} 와 같은 잠재 변수를 갖는 생성 모델을 예로 들면, 잠재 코드 z\bold{z}의 가능한 값을 모두 살펴보는 것이 어렵기 때문에 계산이 매우 까다롭다.
Flow 기반 deep 생성 모델은 밀도 추정에 대한 강력한 통계적 툴인 normalizing flows의 도움으로 이 어려운 문제를 정복한다. p(x)p(\bold{x})의 좋은 추정을 통해 많은 downstream 작업을 효율적으로 완료할 수 있다. —관찰되지 않았지만 실제 새로운 데이터 포인트를 샘플링하는 것(데이터 생성), 미래 이벤트의 드문 것을 예측하는 것(밀도 추정), 잠재 변수 추론, 물완전한 데이터 샘플 채우기 등.

Types of Generative Models

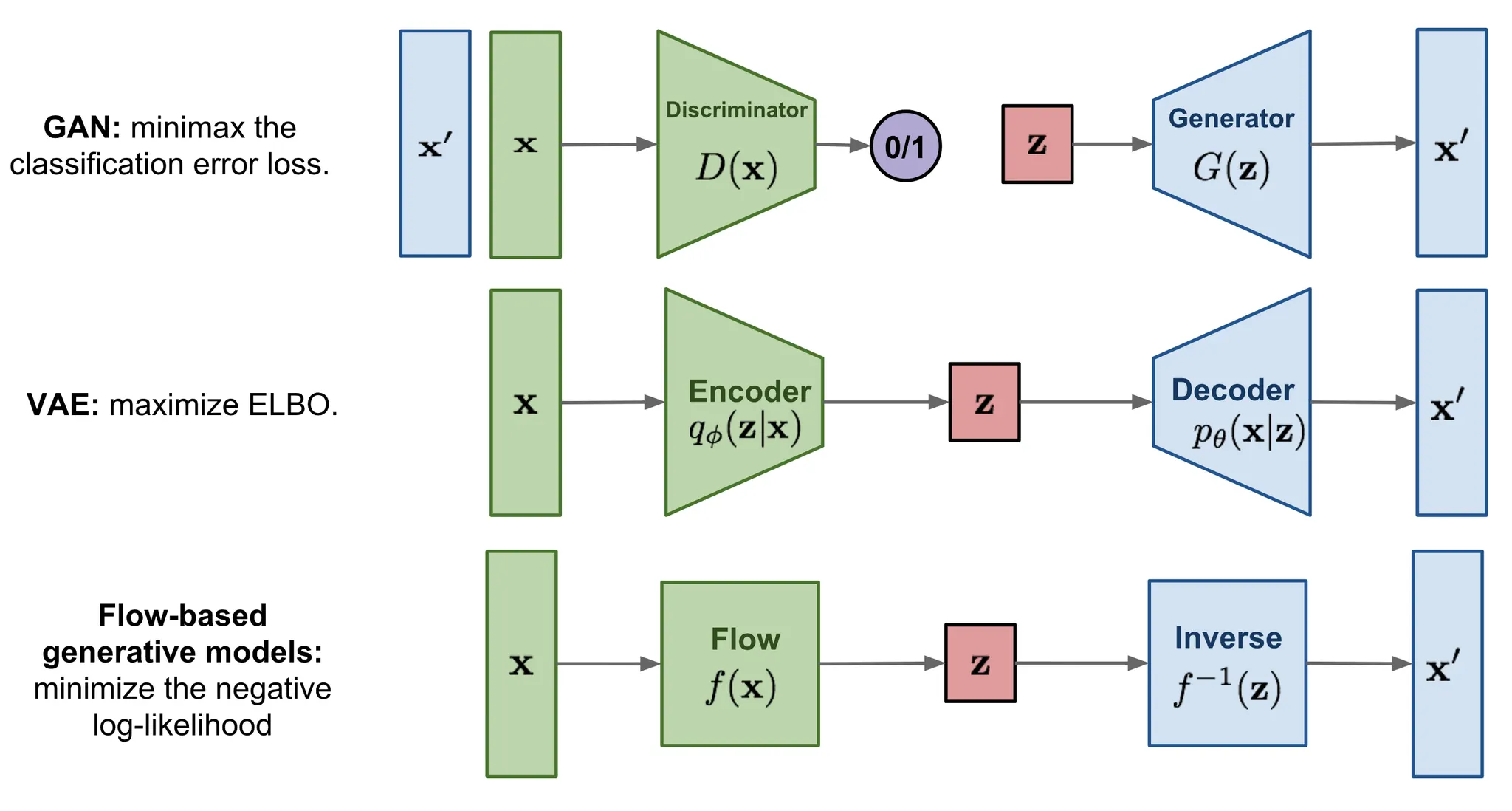
여기서 빠르게 GAN, VAE, flow 기반 생성 모델의 차이를 요약한다.
1.
GAN은 비지도 학습 문제인 데이터 생성을 지도 학습 문제로 모델링하는 영리한 해법을 제공한다. 판별 모델은 생성 모델에 의해 생성된 가짜 샘플에서 실제 데이터를 구분하는 것을 학습한다. 두 모델은 minimax 게임을 플레이 하면서 학습된다.
2.
VAE는 Evidence Lower Bound(ELBO)를 최대화하여 데이터의 log-likelihood를 암시적으로 최적화 한다.
3.
Flow 기반 모델은 가역 변환의 시퀀스로 구성된다. 다른 두 개와 달리 데이터 분포 p(x)p(\bold{x})를 명시적으로 학습하므로 손실 함수는 단순히 음의 log-likelihood이다.

Linear Algebra Basics Recap

flow 기반 모델로 들어가기 전에 2가지 핵심 개념을 이해해야 한다. 야코비안 행렬식과 change of variable rule이다.

Jacobian Matrix and Determinant

nn-차원 입력 벡터 x\bold{x}를 mm-차원 출력 벡터에 매핑하는 함수 f:Rn↦Rm\bold{f} : \mathbb{R}^n \mapsto \mathbb{R}^m이 주어지면 이 함수의 1차 편도함수의 행렬을 Jacobian matrix J\bold{J}라 하고 여기서 i번째 행과 j번째 열의 항목은 Jij=∂fi∂xj\bold{J}_{ij} = {\partial f_i \over \partial x_j}가 된다.
J=[∂f1∂x1…∂f1∂xn⋮⋱⋮∂fm∂x1…∂fm∂xn]\mathbf{J} = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \dots & \frac{\partial f_1}{\partial x_n} \\[6pt] \vdots & \ddots & \vdots \\[6pt] \frac{\partial f_m}{\partial x_1} & \dots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}
행렬식은 정사각 행렬의 모든 요소의 함수로 계산된 1개의 실수이다. 행렬식은 오직 정사각 행렬에만 존재함에 유의하라. 행렬식의 절대값은 ‘행렬의 곱셈이 공간을 얼마나 확장하거나 축소하는지’를 나타내는 척도로 생각할 수 있다.
n×nn \times n 행렬 M\bold{M}의 행렬식은 다음과 같다.
det⁡M=det⁡[a11a12…a1na21a22…a2n⋮⋮⋮an1an2…ann]=∑j1j2…jn(−1)τ(j1j2…jn)a1j1a2j2…anjn\det M = \det \begin{bmatrix}a_{11} & a_{12} & \dots & a_{1n} \\a_{21} & a_{22} & \dots & a_{2n} \\\vdots & \vdots & & \vdots \\a_{n1} & a_{n2} & \dots & a_{nn} \\\end{bmatrix} = \sum_{j_1 j_2 \dots j_n} (-1)^{\tau(j_1 j_2 \dots j_n)} a_{1j_1} a_{2j_2} \dots a_{nj_n}
여기서 합산 j1j2...jnj_1j_2...j_n 아래 첨자는 집합 {1,2,...,n}\{1,2,..., n\}의 모든 순열(permutation)이므로 총 n!n!의 항목이 존재한다. τ(.)\tau(.)은 순열의 signature를 지시한다.
정사각행렬 M\bold{M}의 행렬식은 그것이 가역인지 아닌지를 결정한다. det⁡(M)=0\det(\bold{M}) = 0이면 M\bold{M}은 가역이 아니다. (선형 종속 행이나 열을 갖는 singular 행렬이거나 행이나 열이 모두 0이다.) 반면 det⁡(M)≠0\det(\bold{M}) \ne 0이면 M\bold{M}은 가역이다.
곱의 행렬식은 행렬식의 곱과 동등하다. det⁡(AB)=det⁡(A)det⁡(B)\det(\bold{AB}) = \det(\bold{A})\det(\bold{B})

Change of Variable Theorem

확률 밀도 추정의 맥락에서 change of variable theorem을 구체적으로 리뷰하자. 단일 변수 경우에서 시작한다.
확률 변수 zz가 주어지고 그것의 확률 밀도 함수 z∼π(z)z \sim \pi(z)가 알려지면, 1-1 매핑 함수 x=f(z)x = f(z)를 사용하여 새로운 확률 변수를 구성하기를 원한다. 함수 ff는 가역이므로 z=f−1(x)z = f^{-1}(x)이다. 이제 질문은 새로운 변수 p(x)p(x)의 알려지지 않은 확률 밀도 함수를 어떻게 추론할 수 있을까? 이다.
∫p(x)dx=∫π(z)dz=1   ; Definition of probability distribution.p(x)=π(z)∣dzdx∣=π(f−1(x))∣df−1dx∣=π(f−1(x))∣(f−1)′(x)∣\begin{aligned}& \int p(x)dx = \int \pi(z)dz = 1 \scriptstyle{\text{   ; Definition of probability distribution.}}\\& p(x) = \pi(z) \left\vert\frac{dz}{dx}\right\vert = \pi(f^{-1}(x)) \left\vert\frac{d f^{-1}}{dx}\right\vert = \pi(f^{-1}(x)) \vert (f^{-1})'(x) \vert\end{aligned}
(∫p(x)dx=∫π(z)dz=1\int p(x)dx = \int \pi(z)dz = 1는 정의에 의해 주어진 것이고, 위 식을 xx로 미분하면 p(x)=π(z)∣dzdx∣p(x) = \pi(z)|{dz \over dx}|가 됨. 또한 z=f−1(x)z = f^{-1}(x)로 정의했으므로 그 이후로 식이 전개 됨)
정의에 의해 적분 ∫π(z)dz\int \pi(z)dz는 극소의 너비 Δz\Delta z의 사각형의 무한 수의 합이다. 위치 zz에서 이런 사각형의 가장 높이는 밀도 함수 π(z)\pi(z)의 값이다. 변수를 교체하면 z=f−1(x)z = f^{-1}(x)는 ΔzΔx=(f−1(x))′{\Delta z \over \Delta x} = (f^{-1}(x))'과 Δz=(f−1(x))′Δx\Delta z = (f^{-1}(x))'\Delta x를 산출한다. 여기서 ∣(f−1(x))′∣|(f^{-1}(x))'|는 변수 zz와 xx의 서로 다른 두 좌표에서 각각 정의되는 사각형의 면적 사이의 비율을 나타낸다.
다변량 버전도 유사한 형식을 갖는다.
z∼π(z),x=f(z),z=f−1(x)p(x) =π(z)∣det⁡dzdx∣  =π(f−1(x))∣det⁡df−1dx∣\begin{aligned}\mathbf{z} &\sim \pi(\mathbf{z}), \mathbf{x} = f(\mathbf{z}), \mathbf{z} = f^{-1}(\mathbf{x}) \\p(\mathbf{x}) &= \pi(\mathbf{z}) \left\vert \det \dfrac{d \mathbf{z}}{d \mathbf{x}} \right\vert  = \pi(f^{-1}(\mathbf{x})) \left\vert \det \dfrac{d f^{-1}}{d \mathbf{x}} \right\vert\end{aligned}
여기서 det⁡∂f∂z\det {\partial \bold{f} \over \partial \bold{z}}는 함수 f\bold{f}의 야코비안 행렬식이다.

What is Normalizing Flows?

좋은 밀도 추정은 머신러닝 문제에서 직접적인 적용을 할 수 있지만 매우 어렵다. 예컨대 딥러닝 모델에서 역전파를 실행해야 하기 때문에 임베딩된 확률 분포(예: posterior p(z∣x)p(\bold{z}|\bold{x}))는 도함수를 쉽고 효율적으로 계산할 수 있을만큼 간단할 것으로 예상된다. 이것이 대부분의 현실세계 분포가 가우시안 보다 더 복잡한데도 가우시안 분포가 잠재 변수 모델에서 자주 사용되는 이유이다.
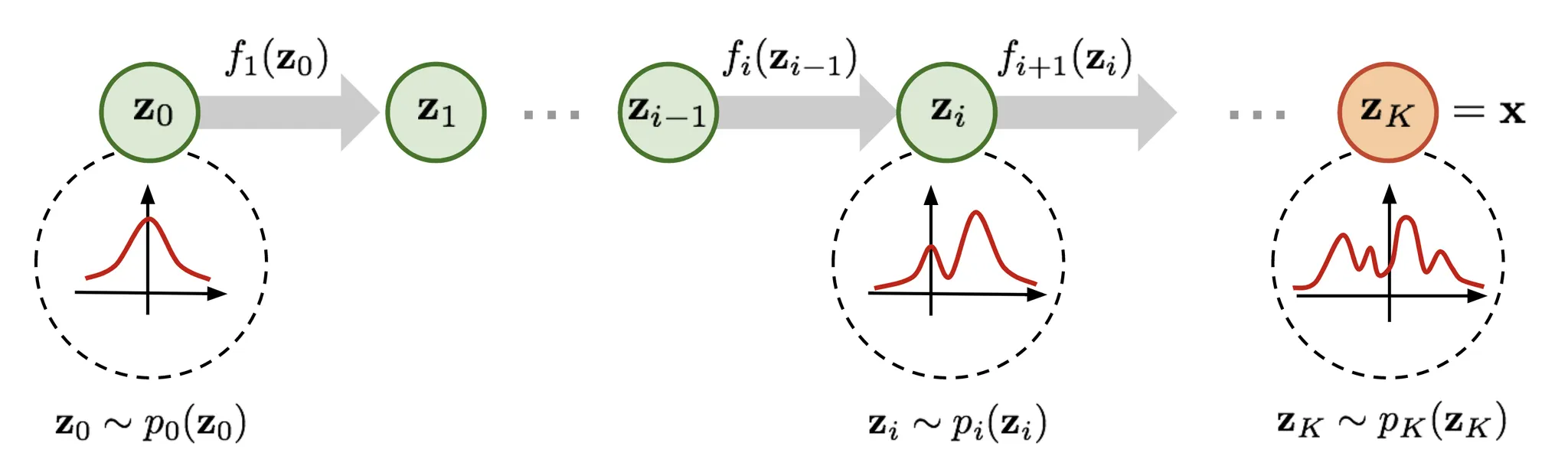
여기서 더 우수하고 강력한 분포 근사를 위해 Normalizing Flow(NF) 모델이 등장한다. normalizing flow 모델은 일련의 가역 변환 함수를 적용하여 단순한 분포를 복잡한 것으로 변환한다. 일련의 변환 과정을 거쳐 change of variables 정리에 따라 변수를 새로운 변수로 반복적으로 대체하고 최종 목표 변수의 확률 분포를 얻는다.
zi−1∼pi−1(zi−1)zi=fi(zi−1), thus zi−1=fi−1(zi)pi(zi) =pi−1(fi−1(zi))∣det⁡dfi−1dzi∣\begin{aligned}\mathbf{z}_{i-1} &\sim p_{i-1}(\mathbf{z}_{i-1}) \\\mathbf{z}_i &= f_i(\mathbf{z}_{i-1})\text{, thus }\mathbf{z}_{i-1} = f_i^{-1}(\mathbf{z}_i) \\p_i(\mathbf{z}_i) &= p_{i-1}(f_i^{-1}(\mathbf{z}_i)) \left\vert \det\dfrac{d f_i^{-1}}{d \mathbf{z}_i} \right\vert\end{aligned}
(zi=fi(zi−1)\bold{z}_i = f_i(\bold{z}_{i-1})이므로 zi−1=fi−1(zi)\bold{z}_{i-1} = f_i^{-1}(\bold{z}_{i})가 성립하고 위와 같이 계산 가능함. 다만 fi≠fi−1f_i \ne f_{i-1}이므로 함수를 chain 형식으로 엮어서 반복 계산해서 단순한 분포에서 복잡한 분포로 바꾼다. 이 부분은 diffusion model에서도 유사하게 사용됨)
그 다음 방정식을 zi\bold{z}_i의 함수로 변환하여 기본 분포를 추론할 수 있다.
pi(zi) =pi−1(fi−1(zi))∣det⁡dfi−1dzi∣=pi−1(zi−1)∣det⁡(dfidzi−1)−1∣; According to the inverse func theorem.=pi−1(zi−1)∣det⁡dfidzi−1∣−1; According to a property of Jacobians of invertible func.log⁡pi(zi)=log⁡pi−1(zi−1)−log⁡∣det⁡dfidzi−1∣\begin{aligned}p_i(\mathbf{z}_i) &= p_{i-1}(f_i^{-1}(\mathbf{z}_i)) \left\vert \det\dfrac{d f_i^{-1}}{d \mathbf{z}_i} \right\vert \\&= p_{i-1}(\mathbf{z}_{i-1}) \left\vert \det \color{red}{\Big(\dfrac{d f_i}{d\mathbf{z}_{i-1}}\Big)^{-1}} \right\vert & \scriptstyle{\text{; According to the inverse func theorem.}} \\&= p_{i-1}(\mathbf{z}_{i-1}) \color{red}{\left\vert \det \dfrac{d f_i}{d\mathbf{z}_{i-1}} \right\vert^{-1}} & \scriptstyle{\text{; According to a property of Jacobians of invertible func.}} \\\log p_i(\mathbf{z}_i) &= \log p_{i-1}(\mathbf{z}_{i-1}) - \log \left\vert \det \dfrac{d f_i}{d\mathbf{z}_{i-1}} \right\vert\end{aligned}
(*) ‘역 함수 정리’에 대한 참고. y=f(x)y = f(x)이면 x=f−1(y)x = f^{-1}(y)이므로 다음이 성립한다.
df−1(y)dy=dxdy=(dydx)−1=(df(x)dx)−1\dfrac{df^{-1}(y)}{dy} = \dfrac{dx}{dy} = \left(\dfrac{dy}{dx}\right)^{-1} = \left(\dfrac{df(x)}{dx}\right)^{-1}
(*) ‘역 함수의 야코비안’에 대한 참고. 가역 행렬의 역함수의 행렬식은 행렬식의 역이다. det⁡(M−1)=(det⁡(M))−1\det(\bold{M}^{-1}) = (\det(\bold{M}))^{-1} 왜냐하면
det⁡(M)det⁡(M−1)=det⁡(M⋅M−1)=det⁡(I)=1\det(\bold{M})\det(\bold{M}^{-1}) = \det(\bold{M} \cdot \bold{M}^{-1}) = \det(\bold{I}) = 1
이러한 확률 밀도 함수의 체인이 주어지면 연속(consecutive) 변수 쌍 사이의 관계를 알 수 있다. 초기 분포 z0\bold{z}_0을 추적할 때까지 출력 x\bold{x}의 방정식을 단계별로 확장할 수 있다.
x=zK=fK∘fK−1∘⋯∘f1(z0)log⁡p(x)=log⁡πK(zK) =log⁡πK−1(zK−1)−log⁡∣det⁡dfKdzK−1∣=log⁡πK−2(zK−2)−log⁡∣det⁡dfK−1dzK−2∣−log⁡∣det⁡dfKdzK−1∣=…=log⁡π0(z0)−∑i=1Klog⁡∣det⁡dfidzi−1∣\begin{aligned}\mathbf{x} = \mathbf{z}_K &= f_K \circ f_{K-1} \circ \dots \circ f_1 (\mathbf{z}_0) \\\log p(\mathbf{x}) = \log \pi_K(\mathbf{z}_K) &= \log \pi_{K-1}(\mathbf{z}_{K-1}) - \log\left\vert\det\dfrac{d f_K}{d \mathbf{z}_{K-1}}\right\vert \\&= \log \pi_{K-2}(\mathbf{z}_{K-2}) - \log\left\vert\det\dfrac{d f_{K-1}}{d\mathbf{z}_{K-2}}\right\vert - \log\left\vert\det\dfrac{d f_K}{d\mathbf{z}_{K-1}}\right\vert \\&= \dots \\&= \log \pi_0(\mathbf{z}_0) - \sum_{i=1}^K \log\left\vert\det\dfrac{d f_i}{d\mathbf{z}_{i-1}}\right\vert\end{aligned}
확률 변수 zi=fi(zi−1)\mathbf{z}_i = f_i(\mathbf{z}_{i-1})가 통과하는 경로가 flow이고 연속(successive) 분포 πi\pi_i에 의해 형성된 전체 체인을 normalizing flow라고 부른다. 방정식에서 계산에 필요한 변환 함수 fif_i는 두 가지 속성을 만족해야 한다.
1.
쉽게 가역이어야 한다.
2.
야코비안 행렬식을 쉽게 계산할 수 있어야 한다.

Models with Normalizing Flows

우리의 도구 상자에서 normalizing flow를 사용하면, 입력 데이터 log⁡p(x)\log p(\bold{x})의 정확한 log likelihood는 다루기 용이해진다. 결과적으로 flow 기반 생성 모델의 학습 기준은 학습 데이터셋 D\mathcal{D}에 대한 negative log likelihood(NLL)이다.
L(D)=−1∣D∣∑x∈Dlog⁡p(x)\mathcal{L}(\mathcal{D}) = - \frac{1}{\vert\mathcal{D}\vert}\sum_{\mathbf{x} \in \mathcal{D}} \log p(\mathbf{x})

RealNVP

RealNVP(Real-valued Non-Volume Preserving) 모델은 가역 전단사(bijective) 변환 함수의 시퀀스를 stacking 하여 normalizing flow를 구현한다. affine coupling layer라 불리는 각 전단사 f:x↦yf : \bold{x} \mapsto \bold{y}에서 입력 차원은 두 부분으로 분할된다.
•
첫 dd 차원은 동일하게 유지된다.
•
두 번째 부분 d+1d+1에서 DD 차원은 affine 변환(scale-and-shift)를 거치며, scale과 shift 파라미터는 모두 처음 dd 차원의 함수이다.
y1:d=x1:d yd+1:D=xd+1:D⊙exp⁡(s(x1:d))+t(x1:d)\begin{aligned}\mathbf{y}_{1:d} &= \mathbf{x}_{1:d} \\ \mathbf{y}_{d+1:D} &= \mathbf{x}_{d+1:D} \odot \exp({s(\mathbf{x}_{1:d})}) + t(\mathbf{x}_{1:d})\end{aligned}
여기서 s(.)s(.)과 t(.)t(.)는 scale과 transition 함수이고 모두 Rd↦RD−d\mathbb{R}^d \mapsto \mathbb{R}^{D-d}에 매핑된다. ⊙\odot 연산자는 요소별 곱이다.
이제 이 변환이 flow 변환에 대한 두 가지 기본 속성을 만족하는지 체크하자.
조건 1: 가역이어야 함.
그렇다 그리고 이것은 꽤 간단하다.
{y1:d=x1:d yd+1:D=xd+1:D⊙exp⁡(s(x1:d))+t(x1:d)⇔ {x1:d=y1:d xd+1:D=(yd+1:D−t(y1:d))⊙exp⁡(−s(y1:d))\begin{cases}\mathbf{y}_{1:d} &= \mathbf{x}_{1:d} \\ \mathbf{y}_{d+1:D} &= \mathbf{x}_{d+1:D} \odot \exp({s(\mathbf{x}_{1:d})}) + t(\mathbf{x}_{1:d})\end{cases}\Leftrightarrow \begin{cases}\mathbf{x}_{1:d} &= \mathbf{y}_{1:d} \\ \mathbf{x}_{d+1:D} &= (\mathbf{y}_{d+1:D} - t(\mathbf{y}_{1:d})) \odot \exp(-s(\mathbf{y}_{1:d}))\end{cases}
조건 2: 야코비안 행렬식이 쉽게 계산할 수 있어야 함.
그렇다. 이 변환의 야코비안 행렬과 행렬식을 얻는 것은 어렵지 않다. 야코비안은 하삼각 행렬이다.
J= [ Id0d×(D−d) ∂yd+1:D∂x1:ddiag(exp⁡(s(x1:d)))]\mathbf{J} = \begin{bmatrix}  \mathbb{I}_d & \mathbf{0}_{d\times(D-d)} \\[5pt]  \frac{\partial \mathbf{y}_{d+1:D}}{\partial \mathbf{x}_{1:d}} & \text{diag}(\exp(s(\mathbf{x}_{1:d})))\end{bmatrix}
따라서 행렬식은 단순히 대각항의 곱이다.
det⁡(J) =∏j=1D−dexp⁡(s(x1:d))j=exp⁡(∑j=1D−ds(x1:d)j)\det(\mathbf{J}) = \prod_{j=1}^{D-d}\exp(s(\mathbf{x}_{1:d}))_j= \exp(\sum_{j=1}^{D-d} s(\mathbf{x}_{1:d})_j)
지금까지 affine coupling layer는 normalizing flow를 구성하는데 완벽해 보인다.
더 좋은 점은 (1) f−1\bold{f}^{-1}를 계산하는데 s\bold{s}나 t\bold{t}의 역을 계산할 필요가 없고 (2) 야코비안 행렬식을 계산하는데 s\bold{s}나 t\bold{t}의 야코비안을 계산이 포함하지 않기 때문에, 이러한 함수는 임의로 복잡해질 수 있다는 것이다. 즉 s\bold{s}와 t\bold{t} 모두 심층 신경망에 의해 모델링될 수 있다.
하나의 affine coupling layer에서 어떤 차원(channels)은 변하지 않는다. 모든 입력이 변경될 수 있는지 확인하기 위해 모델은 각 레이어의 순서를 반대로 바꾸어 다양한 구성 요소가 변경되지 않은 상태로 유지되도록 한다. 이러한 교대 패턴에 따라 한 변환 레이어에서 동일하게 유지되는 단위 집합은 항상 다음 변환 레이어에서 수정된다. batch normalization은 매우 깊은 coupling 레이어 스택이 있는 모델을 훈련하는데 도움이 되는 것으로 나타났다.
게다가 RealNVP는 multi-scale 아키텍쳐에서 보다 효율적인 모델을 구축할 수 있다. multi-scale 아키텍쳐는 체커보드 패턴 마스킹, squeezing 연산 및 채널별 마스킹을 포함하여 normal affine 레이어에 여러 샘플링 작업을 적용한다.

NICE

NICE(Non-linear Independent Component Estimation) 모델은 RealNVP의 전신이다. NICE의 변환은 additive coupling layer로 알려진 scale 항이 없는 affine coupling layer이다.
{y1:d=x1:d yd+1:D=xd+1:D+m(x1:d)⇔ {x1:d=y1:d xd+1:D=yd+1:D−m(y1:d)\begin{cases}\mathbf{y}_{1:d} &= \mathbf{x}_{1:d} \\ \mathbf{y}_{d+1:D} &= \mathbf{x}_{d+1:D} + m(\mathbf{x}_{1:d})\end{cases}\Leftrightarrow \begin{cases}\mathbf{x}_{1:d} &= \mathbf{y}_{1:d} \\ \mathbf{x}_{d+1:D} &= \mathbf{y}_{d+1:D} - m(\mathbf{y}_{1:d})\end{cases}

Glow

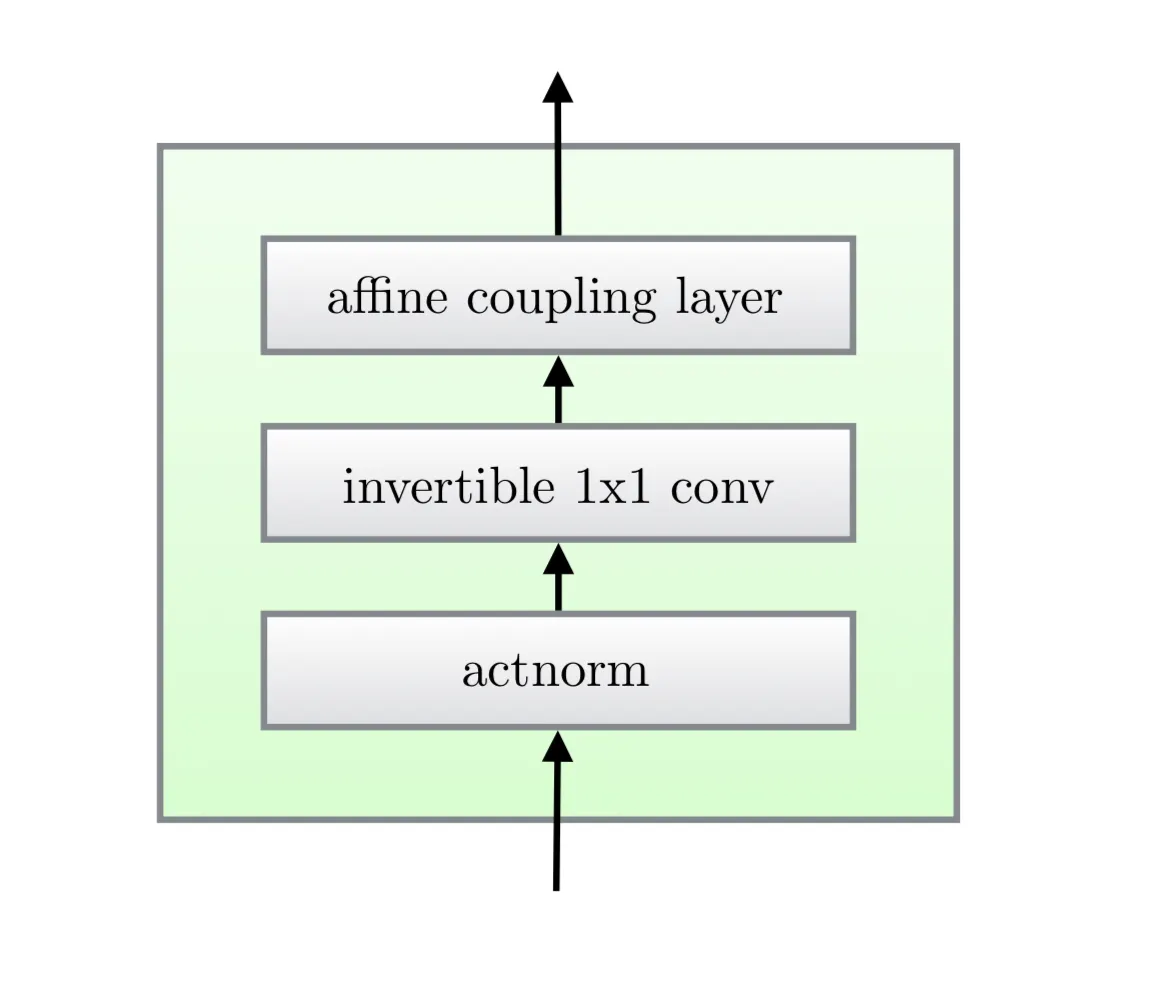
Glow 모델은 이전의 reversible 생성 모델인 NICE와 RealNVP를 확장하고 채널 순서의 역 순열 연산을 가역적 1x1 convolution으로 대체하여 아키텍쳐를 단순화한다.
(이하 Glow 상세 내용 생략)

Models with Autoregressive Flows

autoregressive 제약 조건은 시퀀셜 데이터 x=[x1,...,xD]\bold{x} = [x_1, ..., x_D]를 모델링하는 방법이다. 각 출력은 과거에 관찰된 데이터에만 의존하고 미래에 대해서는 의존하지 않는다. 즉 xix_i를 관찰할 확률은 x1,...,xi−1x_1,...,x_{i-1}에 조건화되고 이러한 조건부 확률의 곱은 전체 시퀀스를 관찰할 확률을 제공한다.
p(x)=∏i=1Dp(xi∣x1,…,xi−1)=∏i=1Dp(xi∣x1:i−1)p(\mathbf{x}) = \prod_{i=1}^{D} p(x_i\vert x_1, \dots, x_{i-1}) = \prod_{i=1}^{D} p(x_i\vert x_{1:i-1})
조건부 밀도를 어떻게 모델링하느냐는 당신의 선택이다. 이것은 x1:i−1x_{1:i-1}의 함수로써 계산된 평균과 표준편차를 갖는 단변량 가우시안이거나 x1:i−1x_{1:i-1}를 입력으로 사용하는 다층 신경망일 수 있다.
normalizing flow의 flow 변환이 autoregressive model로써 구성되는 경우 —벡터 변수의 각 차원은 이전 차원에 조건화 됨— autoregressive flow라고 한다.

MADE

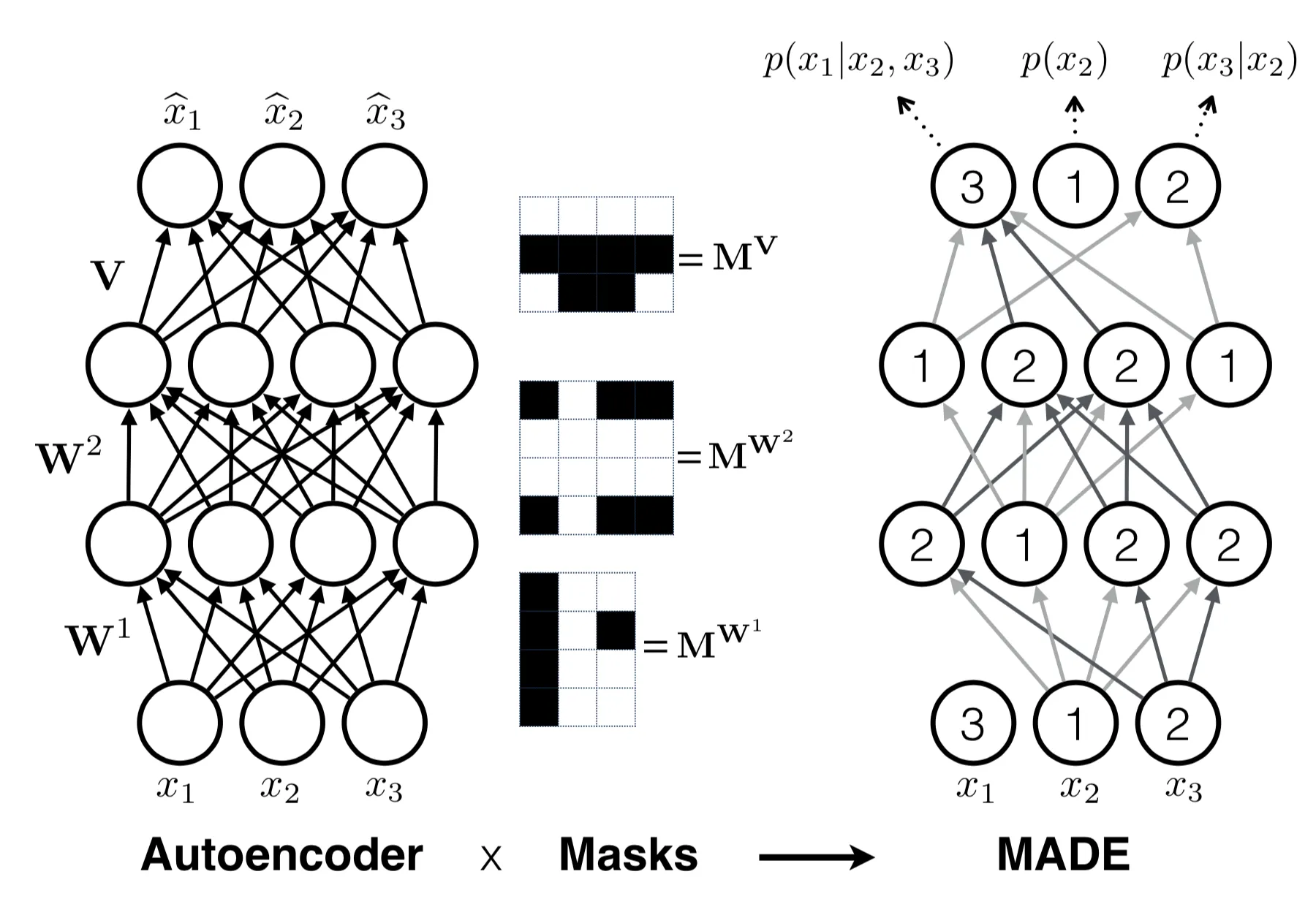
MADE(Masked Autoencoder for Distribution Estimation)은 Autoencoder에서 autoregressive 속성을 효율적으로 적용하기 위해 특별히 설계된 아키텍쳐이다. 조건부 확률을 예측하기 위해 autoencoder를 사용할 때 autoencoder에 서로 다른 관찰 창의 입력을 D번 공급하는 대신 MADE는 이진 마스크 행렬을 곱하여 특정 숨겨진 단위의 기여도를 제거함으로써 각 입력 차원이 단일 패스에서 주어진 순서에 따라 이전 차원에서만 재구성되도록 한다.
다층 fully-connected 신경망에서 가중치 행렬 W1,…,WL\mathbf{W}^1, \dots, \mathbf{W}^L을 가진 LL개의 은닉 레이어와 가중치 행렬 V\bold{V}을 가진 출력 레이어가 있다고 가정하면 출력 x^\hat{\bold{x}}는 각 차원 x^i=p(xi∣x1:i−1)\hat{x}_i = p(x_i\vert x_{1:i-1})을 갖는다.
마스크가 없는 경우 레이어를 통한 계산은 다음과 같다.
h0=xhl=activationl(Wlhl−1+bl)x^=σ(VhL+c)\begin{aligned}\mathbf{h}^0 &= \mathbf{x} \\\mathbf{h}^l &= \text{activation}^l(\mathbf{W}^l\mathbf{h}^{l-1} + \mathbf{b}^l) \\\hat{\mathbf{x}} &= \sigma(\mathbf{V}\mathbf{h}^L + \mathbf{c})\end{aligned}
레이어 간의 연결성을 zero out 하려면 모든 가중치 행렬에 이진 마스크 행렬을 요소 단위로 곱하면 된다. 각 은닉 노드에는 11에서 D−1D-1 사이의 임의의 ‘연결된 정수’가 할당되며 ll-번째 레이어에서 kk-번째 단위로 할당된 값은 mklm_k^l로 표시된다. 이진 마스크 행렬은 두 레이어에 있는 두 노드의 값을 요소별로 비교하여 결정된다.
hl=activationl((Wl⊙MWl)hl−1+bl)x^=σ((V⊙MV)hL+c)Mk′,kWl =1mk′l≥mkl−1 ={  1,if mk′l≥mkl−1  0,otherwiseMd,kV =1d≥mkL ={  1,if d>mkL  0,otherwise\begin{aligned}\mathbf{h}^l &= \text{activation}^l((\mathbf{W}^l \color{red}{\odot \mathbf{M}^{\mathbf{W}^l}}) \mathbf{h}^{l-1} + \mathbf{b}^l) \\\hat{\mathbf{x}} &= \sigma((\mathbf{V} \color{red}{\odot \mathbf{M}^{\mathbf{V}}}) \mathbf{h}^L + \mathbf{c}) \\M^{\mathbf{W}^l}_{k', k} &= \mathbf{1}_{m^l_{k'} \geq m^{l-1}_k} = \begin{cases}    1, & \text{if } m^l_{k'} \geq m^{l-1}_k\\    0, & \text{otherwise}\end{cases} \\M^{\mathbf{V}}_{d, k} &= \mathbf{1}_{d \geq m^L_k} = \begin{cases}    1, & \text{if } d > m^L_k\\    0, & \text{otherwise}\end{cases}\end{aligned}
현재 레이어의 유닛은 이전 레이어의 숫자가 같거나 작은 다른 유닛에만 연결할 수 있으며 이러한 유형의 종속성은 네트워크를 통해 출력 레이어까지 쉽게 전파된다. 모든 단위와 레이어에 숫자가 할당되면 입력 차원의 순서가 고정되고, 그에 따라 조건부 확률이 생성된다. 아래 그림 참조. 모든 은닉 유닛이 어떤 경로를 통해 입력 및 출력 레이어에 연결되어 있는지 확인 하기 위해 최소 연결 정수인 min⁡k’mk’l−1\min_{k’} m_{k’}^{l-1} 보다 크거나 같도록 mklm^l_k를 샘플링한다.
MADE 학습은 다음과 같은 방법으로 더 촉진할 수 있다.
•
순서에 구애받지 않는 학습: 입력 차원을 섞어 MADE가 임의의 순서를 모델링할 수 있도록 하고, 런타임에 autoregressive 모델의 앙상블을 생성할 수 있다.
•
연결성 무관 학습: 모델이 특정 연결성 패턴 제약 조건에 묶이지 않도록 각 학습 미니배치에 대해 mklm_k^l을 다시 샘플링한다.

PixelRNN

(생략)

WaveNet

(생략)

Masked Autoregressive Flow

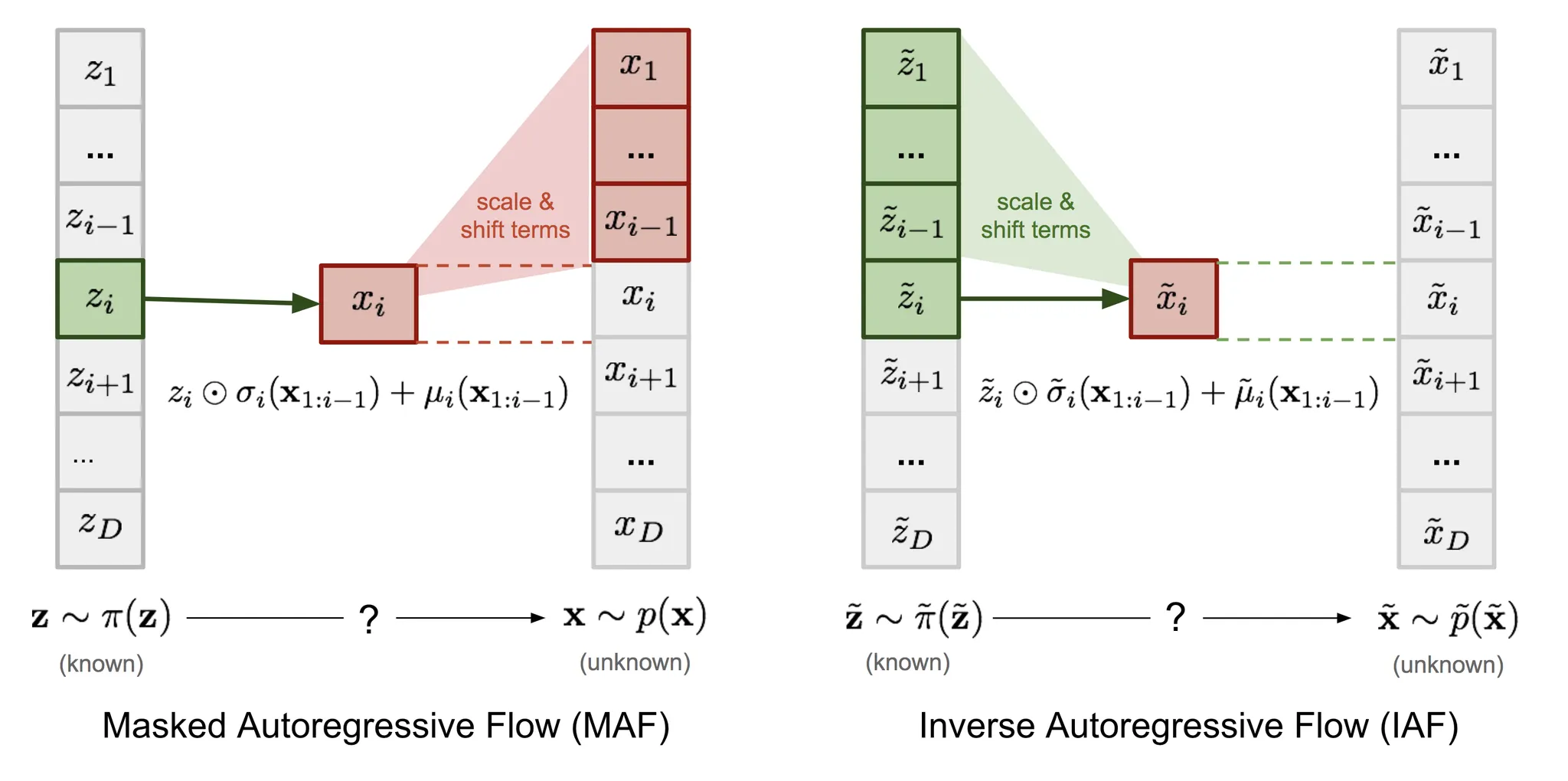
Masked Autoregressive Flow(MAF)는 normalizing flows의 한 유형이다. 여기서 변환 레이어는 autoregressive neural network로 구축된다. MAF는 이후에 소개할 Inverse Autoregressive Flow(IAF)와 유사하다. MAF와 IAF 사이의 관계에 대한 더 많은 논의는 이후 섹션에서 한다.
2개 확률 변수 z∼π(z)\mathbf{z} \sim \pi(\mathbf{z})와 x∼p(x)\mathbf{x} \sim p(\mathbf{x})가 주어지고 확률 밀도 함수 π(z)\pi(\mathbf{z})가 알려지면 MAF는 p(x)p(\mathbf{x})를 학습하는데 초점을 맞춘다. MAF는 과거 차원 x1:i−1\mathbf{x}_{1:i-1}에 조건화 되여 각 xix_i를 생성한다.
정확히 말하면 조건부 확률은 z\mathbf{z}의 affine 변환이고 여기서 scale과 shift 항은 x\mathbf{x}의 관찰된 부분의 함수이다.
•
데이터 생성, 새로운 x\mathbf{x}를 생성한다.
xi∼p(xi∣x1:i−1)=zi⊙σi(x1:i−1)+μi(x1:i−1), where z∼π(z)x_i \sim p(x_i\vert\mathbf{x}_{1:i-1}) = z_i \odot \sigma_i(\mathbf{x}_{1:i-1}) + \mu_i(\mathbf{x}_{1:i-1})\text{, where }\mathbf{z} \sim \pi(\mathbf{z})
•
알려진 x\mathbf{x}가 주어질 때 밀도 추정
p(x)=∏i=1Dp(xi∣x1:i−1)p(\mathbf{x}) = \prod_{i=1}^D p(x_i\vert\mathbf{x}_{1:i-1})
생성 절차는 순차적이기 때문에 설계 상 느리다. 반면 밀도 추정은 MADE와 같은 아키텍쳐를 사용하여 네트워크를 한 번만 통과하면 된다. 변환 함수는 가역과 야코비안 행렬식이 계산하기 쉽다는게 자명하다.

Inverse Autoregressive Flow

Inverse Autoregressive flow(IAF)는 MAF와 유사하게 target 변수의 조건부 확률도 autoregressive 모델로 모델링하지만 reversed flow를 사용하여 더 효율적인 샘플링 절차를 달성한다.
우선 MAF에서 affine 변환의 역을 한다.
zi=xi−μi(x1:i−1)σi(x1:i−1)=−μi(x1:i−1)σi(x1:i−1)+xi⊙1σi(x1:i−1)z_i = \frac{x_i - \mu_i(\mathbf{x}_{1:i-1})}{\sigma_i(\mathbf{x}_{1:i-1})} = -\frac{\mu_i(\mathbf{x}_{1:i-1})}{\sigma_i(\mathbf{x}_{1:i-1})} + x_i \odot \frac{1}{\sigma_i(\mathbf{x}_{1:i-1})}
만일 다음이라 하면
x~=z, p~(.)=π(.), x~∼p~(x~)z~=x, π~(.)=p(.), z~∼π~(z~)μ~i(z~1:i−1)=μ~i(x1:i−1)=−μi(x1:i−1)σi(x1:i−1)σ~(z~1:i−1)=σ~(x1:i−1)=1σi(x1:i−1)\begin{aligned}& \tilde{\mathbf{x}} = \mathbf{z}\text{, }\tilde{p}(.) = \pi(.)\text{, }\tilde{\mathbf{x}} \sim \tilde{p}(\tilde{\mathbf{x}}) \\& \tilde{\mathbf{z}} = \mathbf{x} \text{, }\tilde{\pi}(.) = p(.)\text{, }\tilde{\mathbf{z}} \sim \tilde{\pi}(\tilde{\mathbf{z}})\\& \tilde{\mu}_i(\tilde{\mathbf{z}}_{1:i-1}) = \tilde{\mu}_i(\mathbf{x}_{1:i-1}) = -\frac{\mu_i(\mathbf{x}_{1:i-1})}{\sigma_i(\mathbf{x}_{1:i-1})} \\& \tilde{\sigma}(\tilde{\mathbf{z}}_{1:i-1}) = \tilde{\sigma}(\mathbf{x}_{1:i-1}) = \frac{1}{\sigma_i(\mathbf{x}_{1:i-1})}\end{aligned}
그러면 다음을 얻는다.
x~i∼p(x~i∣z~1:i)=z~i⊙σ~i(z~1:i−1)+μ~i(z~1:i−1), where z~∼π~(z~)\tilde{x}_i \sim p(\tilde{x}_i\vert\tilde{\mathbf{z}}_{1:i}) = \tilde{z}_i \odot \tilde{\sigma}_i(\tilde{\mathbf{z}}_{1:i-1}) + \tilde{\mu}_i(\tilde{\mathbf{z}}_{1:i-1})\text{, where }\tilde{\mathbf{z}} \sim \tilde{\pi}(\tilde{\mathbf{z}})
IAF는 π~(z~)\tilde{\pi}(\tilde{\mathbf{z}})가 알려졌다는 가정하에 x~\tilde{\mathbf{x}}의 확률 밀도 함수를 추정하려고 한다. inverse flow도 MAF와 마찬가지로 autoregressive affine 변환이지만 scale과 shift 항은 알려진 분포 π~(z~)\tilde{\pi}(\tilde{\mathbf{z}})에서 관측된 변수의 autoregressive 함수이다. 아래 그림에서 MAF와 IAF를 비교하라.
개별 요소 x~i\tilde{x}_i의 계산은 서로 의존하지 않으므로 쉽게 병렬화 할 수 있다. (MADE를 사용하면 한 번만 통과). 알려진 x~\tilde{\mathbf{x}}에 대한 밀도 추정은 z~i=(x~i−μ~i(z~1:i−1))/σ~i(z~1:i−1)\tilde{z}_i = (\tilde{x}_i - \tilde{\mu}_i(\tilde{\mathbf{z}}_{1:i-1})) / \tilde{\sigma}_i(\tilde{\mathbf{z}}_{1:i-1}), 즉 D번의 순차적인 순서로 z~i\tilde{z}_i를 구해야 하므로 효율적이지 않다.
MAF
IAF
Base 분포
z∼π(z)\mathbf{z}\sim\pi(\mathbf{z})
z~∼π~(z~)\tilde{\mathbf{z}}\sim\tilde{\pi}(\tilde{\mathbf{z}})
Target 분포
x∼p(x)\mathbf{x}\sim p(\mathbf{x})
x~∼p~(x~)\tilde{\mathbf{x}}\sim\tilde{p}(\tilde{\mathbf{x}})
모델
xi=zi⊙σi(x1:i−1)+μi(x1:i−1)x_i = z_i \odot \sigma_i(\mathbf{x}_{1:i-1}) + \mu_i(\mathbf{x}_{1:i-1})
x~i=z~i⊙σ~i(z~1:i−1)+μ~i(z~1:i−1)\tilde{x}_i = \tilde{z}_i \odot \tilde{\sigma}_i(\tilde{\mathbf{z}}_{1:i-1}) + \tilde{\mu}_i(\tilde{\mathbf{z}}_{1:i-1})
데이터 생성
Sequential; slow
One pass; fast
밀도 추정
One pass; fast
Sequential; slow

VAE + Flows

Variational Autoencoder(VAE)에서 posterior p(z∣x)p(\bold{z}|\bold{x})를 단순한 가우시안 대신 더 복잡한 분포로 모델링하려는 경우, 더 나은 밀도 근사를 위해 직관적으로 normalizing flow를 사용하여 기본 가우시안으로 변환할 수 있다. 그러면 encoder는 입력 x\bold{x}의 함수인 scale과 shift 항 (μi,σi)(\mu_i, \sigma_i) 집합을 예측한다.
Made with