Search
Duplicate

AI/ Recurrent Neural Network(RNN)

Recurrent Neural Network(RNN)

Recurrent Neural Network(RNN)은 시퀀스의 입력 공간에서 시퀀스의 출력 공간으로 stateful 한 방법으로 매핑하는 모델이다. 이것은 출력의 예측 yt\bold{y}_t이 입력 xt\bold{x}_t에만 의존하는게 아니라 시퀀스가 진행되면서 시간에 대해 업데이트 되는 시스템의 은닉 상태 ht\bold{h}_t에도 의존한다는 것을 의미한다.
관찰과 은닉 상태 존재하고 그것들이 시퀀스에 따라 변하기 때문에 RNN은 Hidden Markov Model(HMM)이나 State-Space Model(SSM)의 변형으로 생각할 수 있다. RNN은 입력과 관찰의 형식에 따라 다양항 모델 형식을 갖는데, 크게 Sequence Generation(Vec2Seq), Sequence Classification(Seq2Vec), Sequence Translation(Seq2Seq)의 형식으로 구분할 수 있다.

Vec2Seq (sequence generation)

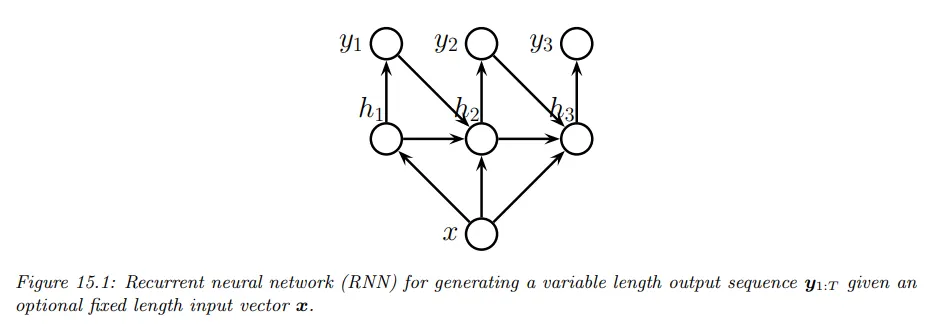
RNN 중 vector to sequence 형식을 sequence generation이라 한다. 하나의 입력 벡터에서 은닉 상태를 업데이트하고 은닉 상태에서 출력 벡터를 생성한다. 그 후 다음 시퀀스에서 입력과 이전 출력 벡터를 이용해서 은닉 상태를 업데이트 하고 새로운 출력 벡터를 생성하고 반복한다. 아래 그림 참조.
해당하는 모델은 다음과 같이 주어진다.
p(y1:T∣x)=∑h1:Tp(y1:T,h1:T∣x)=∑h1:T∏t=1Tp(yt∣ht)p(ht∣ht−1,yt−1,x)p(\bold{y}_{1:T}|\bold{x}) = \sum_{\bold{h}_{1:T}} p(\bold{y}_{1:T}, \bold{h}_{1:T}|\bold{x}) = \sum_{\bold{h}_{1:T}} \prod_{t=1}^{T} p(\bold{y}_t|\bold{h}_t)p(\bold{h}_t|\bold{h}_{t-1},\bold{y}_{t-1},\bold{x})
출력 분포는 일반적으로 다음과 같이 주어진다.
p(yt∣ht)=Cat(yt∣softmax(Whyht+by))p(\bold{y}_t|\bold{h}_t) = \text{Cat}(\bold{y}_t|\text{softmax}(\bold{W}_{hy}\bold{h}_t + \bold{b}_y))

Seq2Vec (sequence classification)

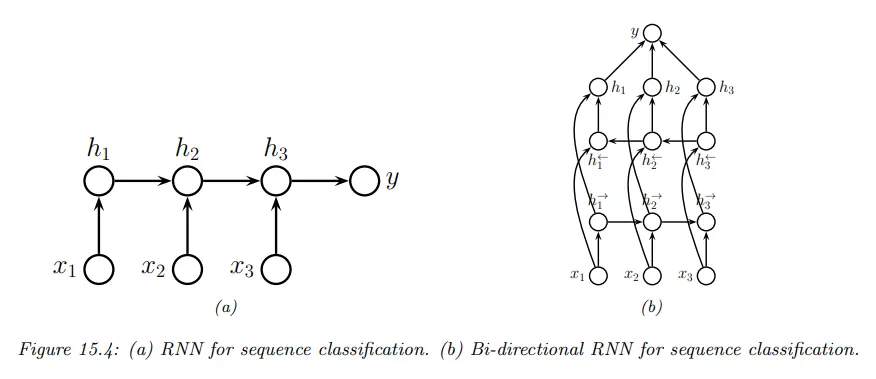
RNN 중 sequence to vector 형식을 sequence classification이라 한다. 가변 길이의 입력 시퀀스에서 순차적으로 은닉 상태를 업데이트 하고 모든 시퀀스가 입력되면 하나의 출력 벡터를 생성한다. 아래 그림 왼쪽 참조.
해당하는 모델은 다음과 같이 주어진다.
p(y∣x1:T)=Cat(y∣softmax(WhT))p(y|\bold{x}_{1:T}) = \text{Cat}(y|\text{softmax}(\bold{Wh}_T))
이러한 형식에 대해 은닉 상태를 과거와 미래의 맥락에 의존하게 만들면 더 좋은 결과를 얻을 수 있다. 이것을 하기 위해 2개의 RNN을 만들고 하나는 forward 방향으로 은닉 상태를 재귀적으로 계산하고, 다른 하나는 backward 방향으로 은닉 상태를 재귀적으로 계산한다. 이것은 bidirectional RNN이라고 한다. 위 그림 오른쪽 참조.

Seq2Seq (sequence translation)

RNN 중 sequence to sequence 형식을 sequence translation이라 한다. 이것은 입력과 출력이 정렬되어 있는 경우와 정렬되지 않은 경우로 구분할 수 있다.

Aligned case

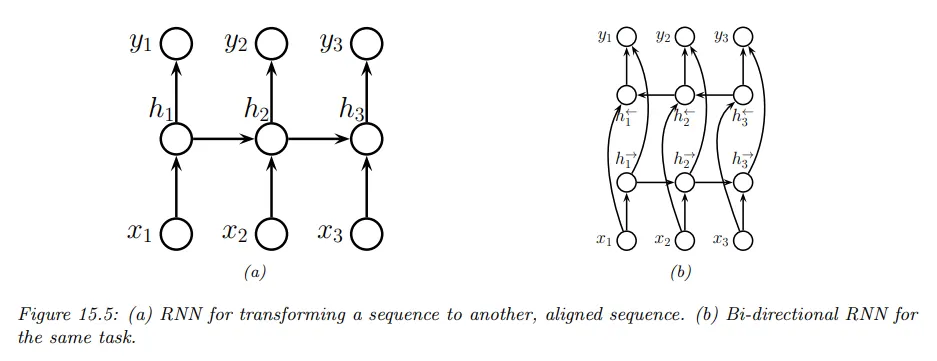
seq2seq의 정렬된 경우의 형식은 가변 길이 입력 시퀀스에서 순차적으로 은닉 상태를 업데이트하고 해당 시점 은닉 벡터에서 출력을 생성한다. 이것은 위치당 하나의 라벨을 예측하기 때문에 밀도 시퀀스 라벨링(dense sequence labeling)으로 생각할 수 있다. 아래 그림 왼쪽 참조.
해당하는 모델은 다음과 같이 주어진다. 여기서 h1=f(h0,x1)=f0(x1)\bold{h}_1 = f(\bold{h}_0, \bold{x}_1) = f_0(\bold{x}_1)을 초기 상태로 정의한다.
p(y1:T∣x1:T)=∑h1:T∏t=1Tp(yt∣ht)I(ht=f(ht−1,xt))p(\bold{y}_{1:T}|\bold{x}_{1:T}) = \sum_{\bold{h}_{1:T}} \prod_{t=1}^T p(\bold{y}_t|\bold{h}_t)\mathbb{I}(\bold{h}_t = f(\bold{h}_{t-1}, \bold{x}_t))
Seq2Vec의 bidirectional RNN을 이 형식에 적용할 수 있다. 위 그림 오른쪽 참조.
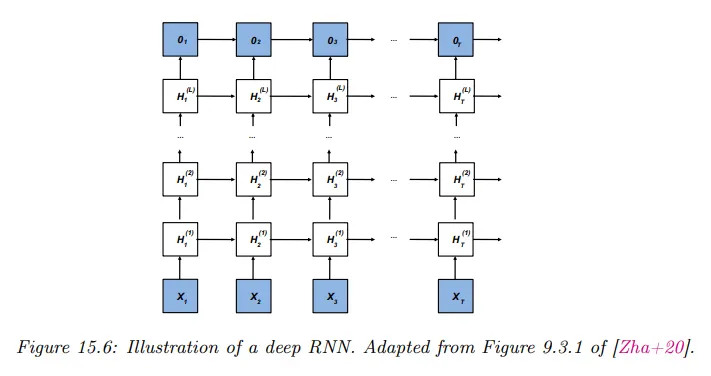
또한 각각의 상단에 여러 은닉 체인을 쌓아서 더 비싼 모델을 만들 수 있다. 아래 그림 참조.

Unaligned case

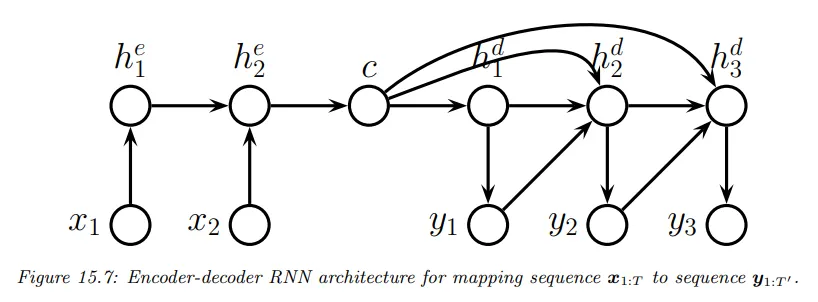
seq2seq의 정렬되지 않은 경우의 형식은 seq2vec 처럼 가변 길이 입력 시퀀스에서 순차적으로 은닉 상태를 업데이트하고, 모든 시퀀스가 입력된 후에 마지막 상태를 이용하여 컨텍스트 벡터 c=fe(x1:T)\bold{c} = f_e(\bold{x}_{1:T})를 생성한 다음 이것과 출력 벡터를 이용해서 출력 시퀀스 y1:T′=fd(c)\bold{y}_{1:T'} = f_d(\bold{c})를 순차적으로 생성한다. 아래 그림 참조.
입력 시퀀스를 받는 은닉 상태와 출력 시퀀스를 생성하는 은닉 상태는 별도의 것으로 각각 encoder, decoder라 한다. 이러한 구조를 encoder-decoder 아키텍쳐라고 하고 기계 번역에 응용 된다.

Backpropagation through time

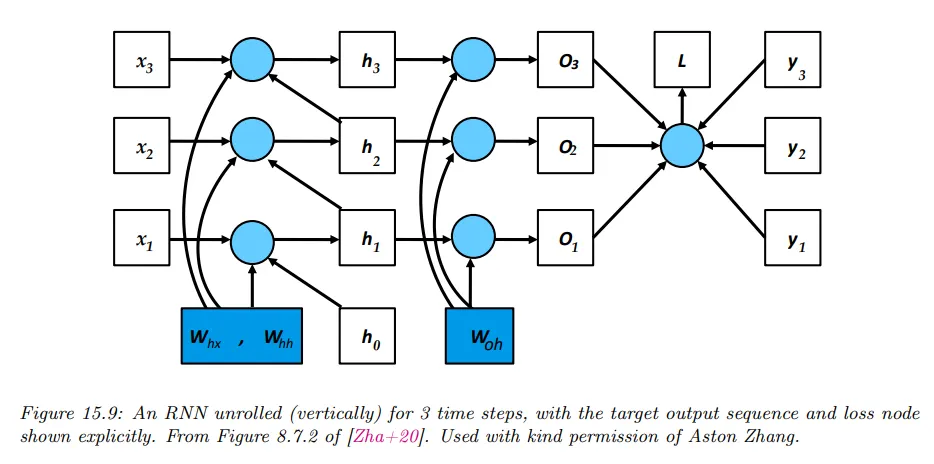
RNN은 sequence 형식이기 때문에 손실의 gradient를 계산하기 위해 아래 그림과 같이 계산 그래프를 펼치고 역전파 알고리즘을 적용한다. 이것을 backpropagation through time(BPTT)라고 부른다.
더 정확하게 다음의 모델을 고려한다. 여기서 ot\bold{o}_t는 출력 logit이고 표기의 단순성을 위해 바이어스 항은 제외했다.
ht=Whxxt+Whhht−1ot=Whoht\begin{aligned} \bold{h}_t &= \bold{W}_{hx}\bold{x}_t + \bold{W}_{hh} \bold{h}_{t-1} \\ \bold{o}_t &= \bold{W}_{ho}\bold{h}_t \end{aligned}
vanila RNN은 시퀀스가 길어지면 vanishing gradient 또는 exploding gradient가 발생할 수 있다. 이에 대한 다양한 해결책이 도입되었는데 LSTM(Long-Short Term Memory)이 그 중 하나이다.

참고

Made with