•
Representation Learning은 CLIP이 끝판을 찍음. 그래서 그 다음으로 Generative Model 쪽으로 관심이 넘어 감.
•
Supervised Learning은 데이터에 대해 Label이 존재함. 그래서 input을 label로 approximation을 하는게 목표.
•
Unsupervised Learning은 데이터만 있고 Label이 없음. 거기서 hidden structure를 학습하는게 목표.
•
generative model은 Unsupervised Learning에 가까움.
◦
현실 데이터에 대해 어떤 확률 분포를 추정함.
◦
그리고 그 분포를 이용해서 데이터를 생성하는게 생성 모델링.
•
생성은 Explicit 방법과 Implicit 방법이 있음.
◦
(Explicit의 현재 대표적인게 diffusion model이고, Implicit의 대표가 GAN)
•
생성 모델링의 예
◦
super-resolution, colorization 등
◦
과학쪽에서는 문제를 잘 푸는게 아니라, 문제를 푸는 과정에서 인사이트를 얻기 위함.
•
생성 모델의 Explicit, Implicit 구분
•
Explicit 모델은 이미지가 주어졌을 때 그 이미지의 확률 분포를 구함.
•
이미지의 픽셀들의 순서를 일단 정함.
•
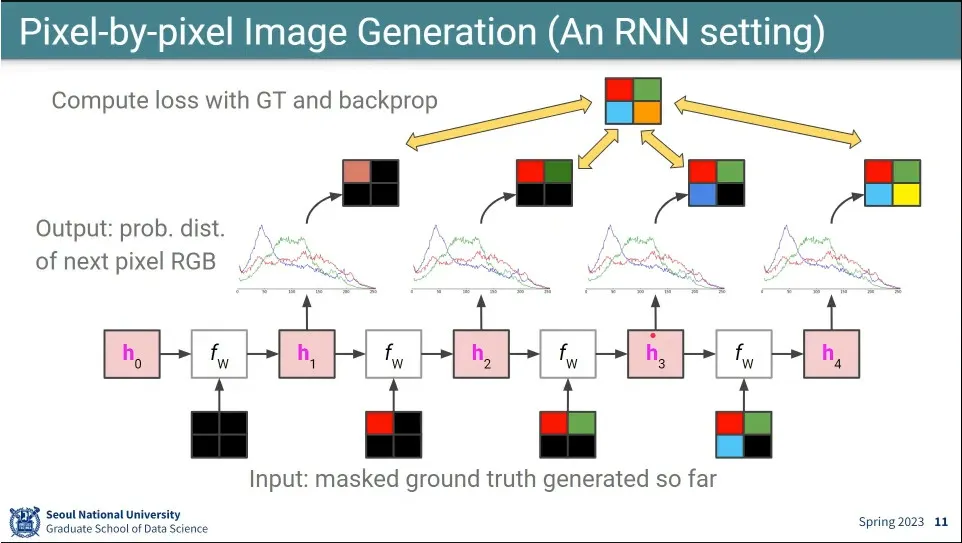
이미지가 주어지면 그 분포를 만들고, 그 분포를 통해 새로 그려져야 할 pixel을 결정함.
◦
그렇게 결정된 pixel을 다시 분포에 넣고 그 다음 pixel을 예측함. auto-regressive.
•
이번 픽셀의 확률 분포를 예측하기 위해 이전 픽셀들의 값을 이용함.
◦
그것을 3채널에 대해 수행함.
•
이런 방법은 엄청 느림
•
RNN에서 했던 것처럼 pixel을 채워 나감.
•
식은 LSTM과 동일한데, convolution 연산을 하기 때문에 ConvLSTM과 같음
•
기본 흐름
•
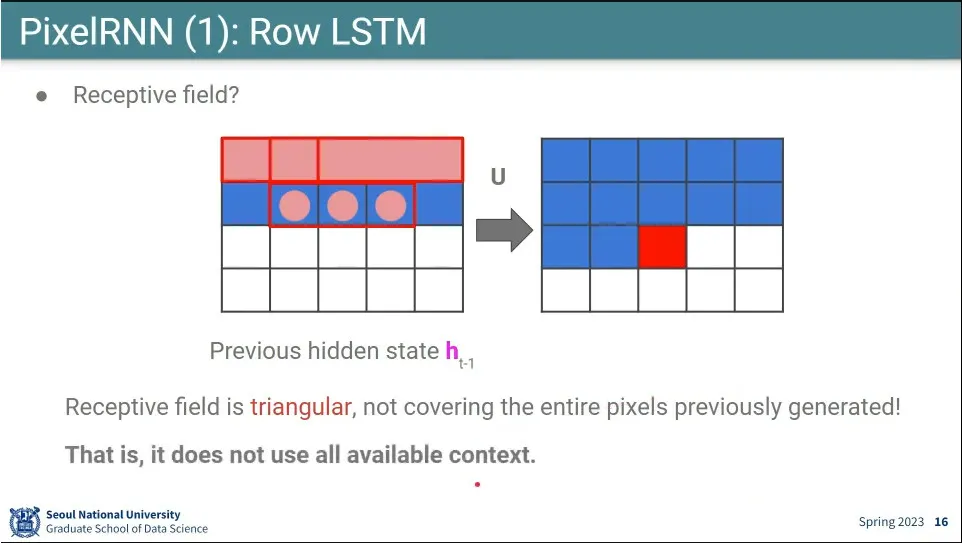
윗줄의 3칸만 보고 현재 픽셀을 결정하면 결국 위로 삼각형으로 생긴 영역만 보고 현재 픽셀을 결정하게 되는데, 이러면 사각 영역이 생기는 문제가 발생함.
•
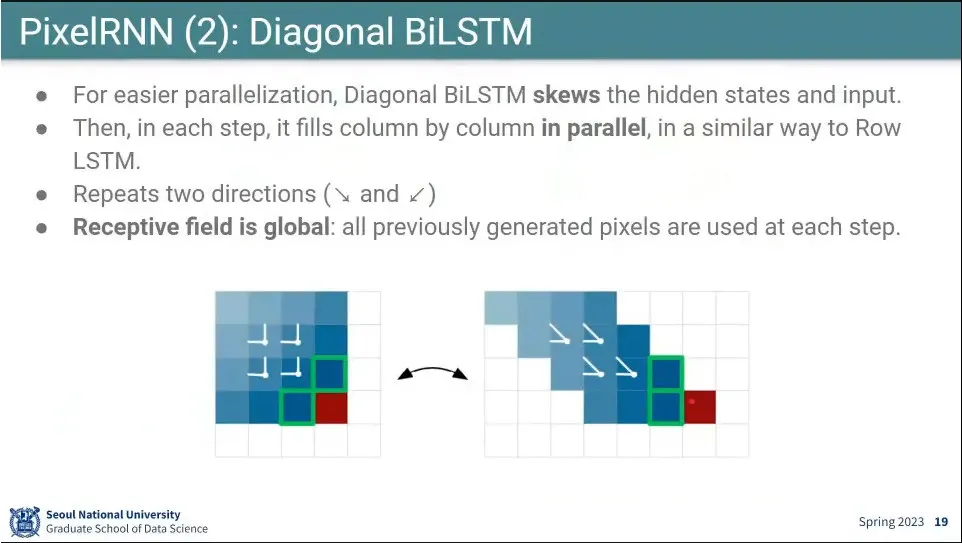
그 문제를 해결하기 위해 대각선 방향을 보는 버전이 나옴.
•
위 줄의 3칸을 보는게 아니라, 대각선 방향으로 참고함.
•
계산 성능을 위해 이미지를 기울인 후에 1x1 conv를 써서 계산 함.
•
추가로 대각선을 왼쪽 위에서 오른쪽 아래로 내려가는 방향과 오른쪽 위에서 왼쪽 아래로 내려가는 2가지 방향으로 돌림.
•
그 다음으로 나온게 (사실 3개가 한 논문에 나옴) convolution을 이용해서 픽셀을 생성함.
◦
이때 아직 안 만들어진 영역은 참고가 안되므로 masking해서 돌림.
•
inference는 순차적으로 해야하지만, training은 parallel로 처리 가능. 그래서 기존 pixel rnn보다 pixel cnn이 더 빠름.
•
mask를 씌울 때 처음 input에 대해서는 현재 생성해야 하는 pixel을 보면 안되므로 가리는데, conv를 여러층 쌓으면 그 위층에서는 현재 pixel 위치의 것을 봐도 됨. 그래서 mask가 2개가 쓰임.
•
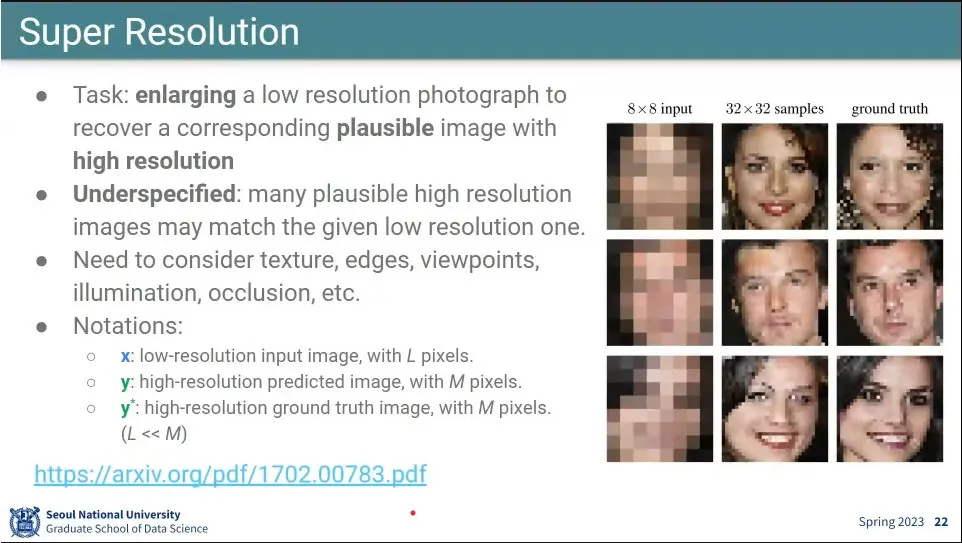
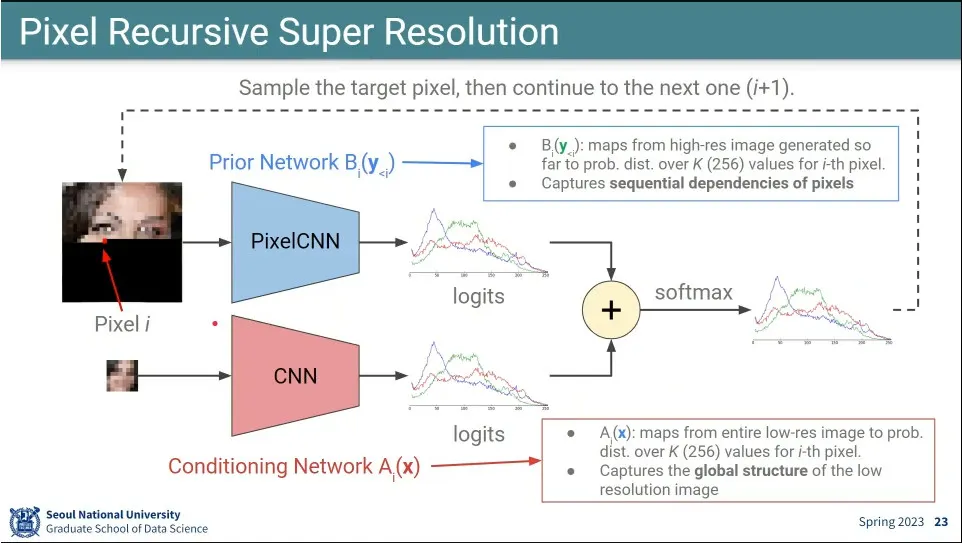
pixel cnn으로 Super Resolution이 가능함
•
픽셀을 생성하는 pixel cnn과, 저해상도를 고해상도로 올리는 cnn 모델 2개를 두고 그 둘을 합쳐서 최종 결과를 만듦.
•
A, B 모델의 합에 softmax를 씌워서 확률 분포를 정의 함.
•
loss는 그 분포에 대해 cross-entropy를 사용.
•
확률 분포에서 sampling 해서 사용하기 때문에 inference 할 때마다 조금씩 다른 결과가 나옴.
•
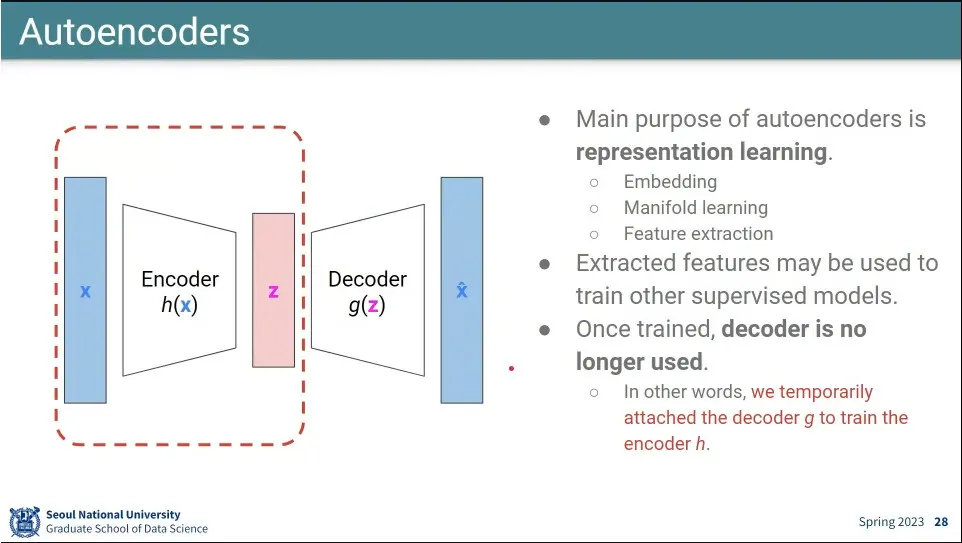
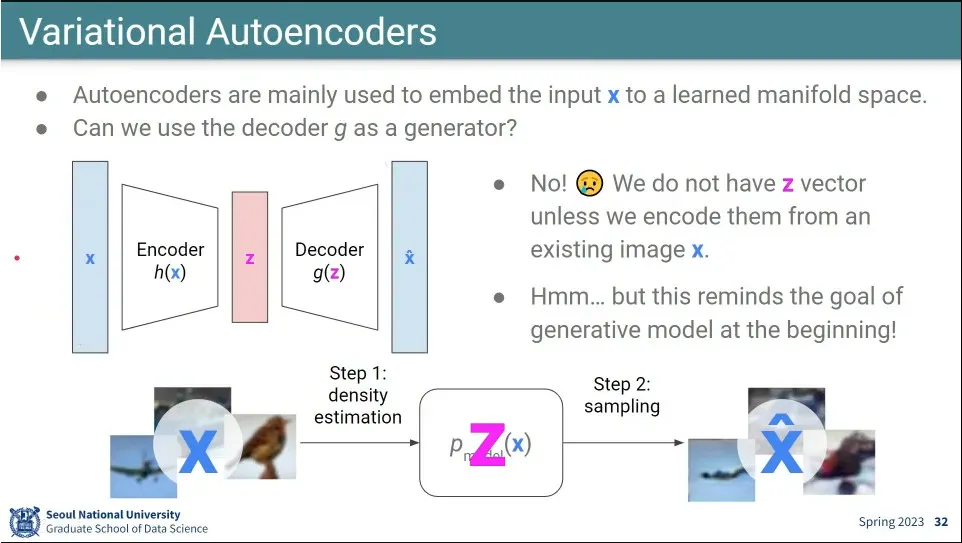
Autoencoder는 저차원 공간으로 압축 시켰다가 다시 원래로 복원하면서, 이미지를 원본과 똑같이 복원하기 위해 핵심적인 feature를 배우게 하는게 목표
◦
이것은 어느 도메인에든 사용 가능.
◦
Autoencoder는 Variational Auto Encoder를 이해하기 위해 설명. 이거 자체는 생성 모델이 아님.
•
loss는 squared loss를 줌.
•
Autoencoder는 z로 압축하는게 중요하고 복원하는 것은 별로 중요하지 않기 때문에 Encoder 부분이 중요함.
•
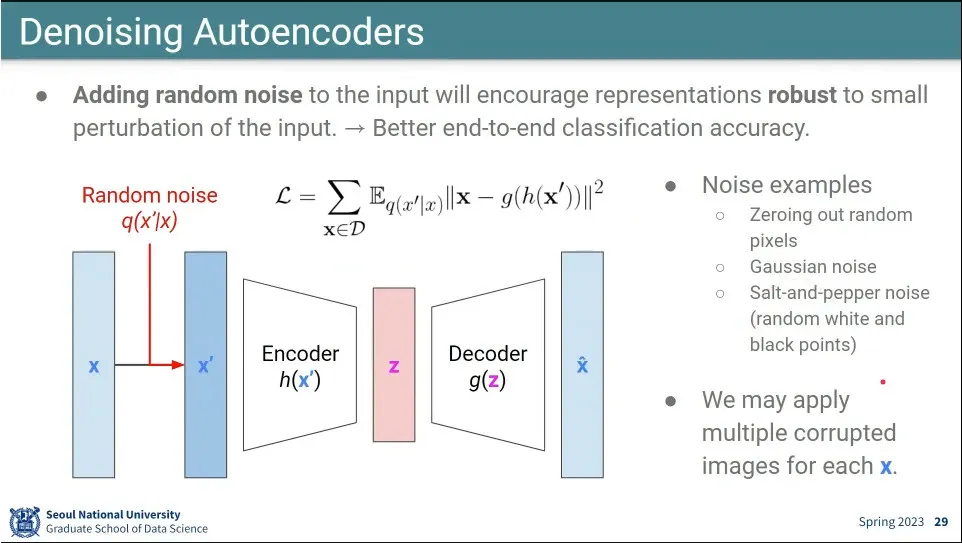
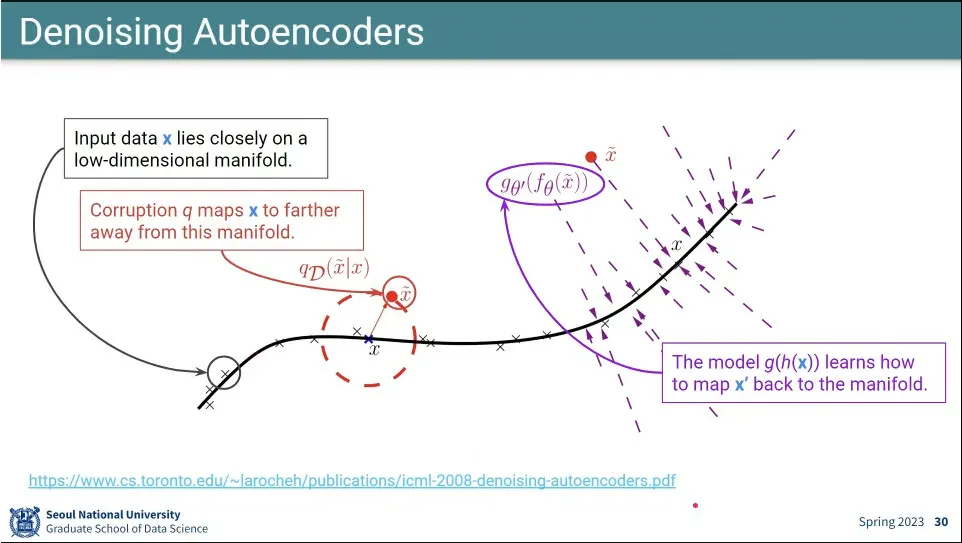
Autoencoder의 변형으로 input에 noise를 준 후 원본으로 복원시키는 것이 있는데, 이게 Denoising Autoencoder.
◦
이러면 좀 더 잘 된다고 함.
•
랜덤하게 noise를 주면 denoising 과정도 같이 배우게 됨.
•
Autoencoder를 이용해서 생성 모델로 쓰려고 했는데, 그걸로는 잘 안 됨.
•
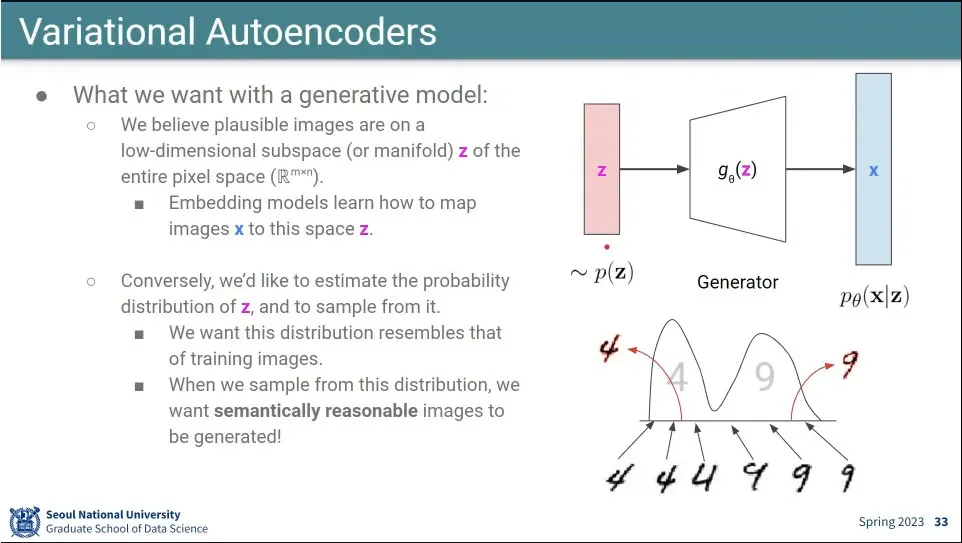
확률 분포를 잘 만들어 주면 될 것 같아서, z가 어떤 확률 분포를 모사하도록 만들어주자는게 Variational Autoencoder의 아이디어
◦
(VAE에 쓰인 수학은 이후 diffusion model에까지 이어지기 때문에 잘 이해해야 함)
•
이미지는 z에 대해 generator를 통과시켜 만들 수 있으므로, 이 세상의 모든 이미지를 z의 확률 분포와 generator 확률 분포를 곱해서 적분하면 만들 수 있다는게 첫 번째 가정.
◦
•
그런데 모든 현실의 모든 이미지들을 가질 수 없으므로, 우리가 가진 샘플들의 합으로 p(x)를 approximate 한다.
◦
•
그리고 그 합을 기대값으로 표현할 수 있음.
◦
•
확률 분포의 모든 곱을 Likelihood로 정의할 수 있음.
◦
◦
모든 샘플이 iid 라고 가정하고 곱하면 likelihood가 됨.
•
maximum likelihood를 구하기 위해 likelihood 함수에 log를 씌워서 변형 시킴.
◦
◦
log를 곱 안으로 넣으면 sum으로 바뀐다.
•
가 정규 분포를 따른다는 가정을 하고
◦
그 분포를 정규 분포 식에 넣어서 풀면 위 식이 됨.
▪
◦
최종적으로 이식을 maximize 하려면 이 값이 minimize 되어야 함.
◦
그런데 여기서 는 만들어내는 이미지이고 실제 존재하는 이미지인데, 이 식은 이 둘 사이에 squared loss를 구하는 것이 됨.
◦
문제는 이미지에 대해서 squared loss는 오른쪽 아래 이미지와 같이 잘 동작 하지 않음
•
결국 first try는 실패 함.
•
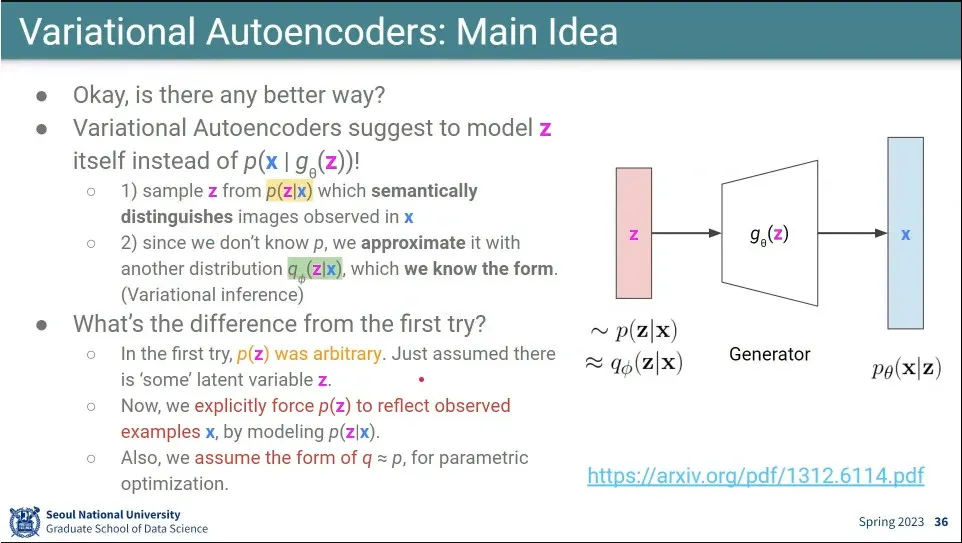
first try에서 가 정규 분포이기만 하면 된다고 했었다가 실패해서 아래 설정을 추가 함
◦
가 아니라 을 사용함. 실제 데이터가 주어졌을 때 정규 분포에서 어떻게 존재해야 하는지를 따라가게 함.
◦
문제는 를 모르기 때문에 이 분포를 모사할 라는 분포를 따로 만듦. 실제 학습 시킬 분포는 가 됨.
•
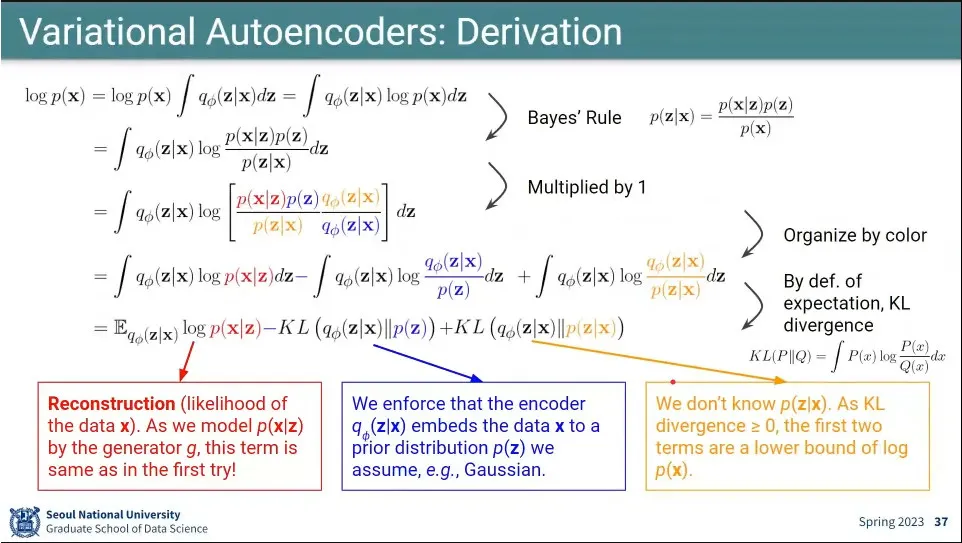
데이터 분포 에서 출발
◦
거기에 1을 곱하는데 를 곱해서 로 만듦
▪
어떤 확률 분포든 전체 합은 1이 되기 때문
◦
를 적분 안쪽으로 집어 넣어서 로 만듦
◦
베이지안을 써서 식을 부분을 바꿔서 로 만듦
◦
거기에 다시 1을 곱하는데 를 곱해서 식을 로 만듦
◦
log 안쪽에 있는 것을 각각 분배해서 쓰면 아래와 같이 분리 됨
▪
◦
여기서 는 기대값 가 됨
▪
에 대한 확률 분포 을 따르는 의 기댓값.
◦
여기서 는 KL-다이버전스의 정의를 따라 가 됨
◦
여기서 는 KL-다이버전스의 정의를 따라 가 됨
•
최종적으로 만들어진 식을 maximize 하는게 목표인데
◦
그러려면 맨 앞의 식이 커져야 함. 이거는 first try의 과 같음.
◦
두 번째 식은 마이너스가 붙어 있으므로 minimize 되어야 하고, 와 가 가까워 져야 함.
▪
이때 는 encoder의 결과이고 이 결과가 어떤 정규 분포 에 가깝게 만들어줘야 함. —정규 분포가 되도록 만들어줘야 함.
◦
세 번째 식은 부산물로 우리가 알 수 있는 값이 아님. 이게 VAE의 한계
•
최종식을 loss 함수로 만들면 위와 같다.
◦
앞선 식의 3번째는 control이 안되니까 빼고 나머지 2개로 loss 함수를 만듦. minimize하기 위해 앞에 마이너스를 붙임
•
이 식을 optimize 하면 generator가 만들어짐.
•
generator를 갖기 위해 앞에 encoder를 붙임.
◦
encoder는 확률 분포 를 만들어 줌
•
학습이 다 되면 encoder를 떼고 decoder만 쓴다.
•
에 그냥 데이터를 떼려 박는게 아니라 확률 분포를 모사하도록 학습 시켰기 때문에 생성 모델이 잘 동작함.
•
encoder는 가우시안 분포로 의 평균과 분산을 배워야 함.
◦
그렇게 만든 가우시안 분포로 를 샘플링 해주고 그걸로 generation을 하면 generation이 된다.
•
input image는 input의 크기를 이용해서 one-hot encoding 함.
◦
실제 해당되는 pixel은 1이고 나머지는 0인 값을 가짐
•
loss 함수의 앞쪽 텀은 generator가 만든 이미지가 실제 이미지와 같아지도록 학습시키는데 cross entropy를 써 줌.
•
loss 함수의 뒷쪽 텀은 2개의 가우시안 분포가 가까워지도록 하는데, 이게 regularization 처럼 작동 함.
•
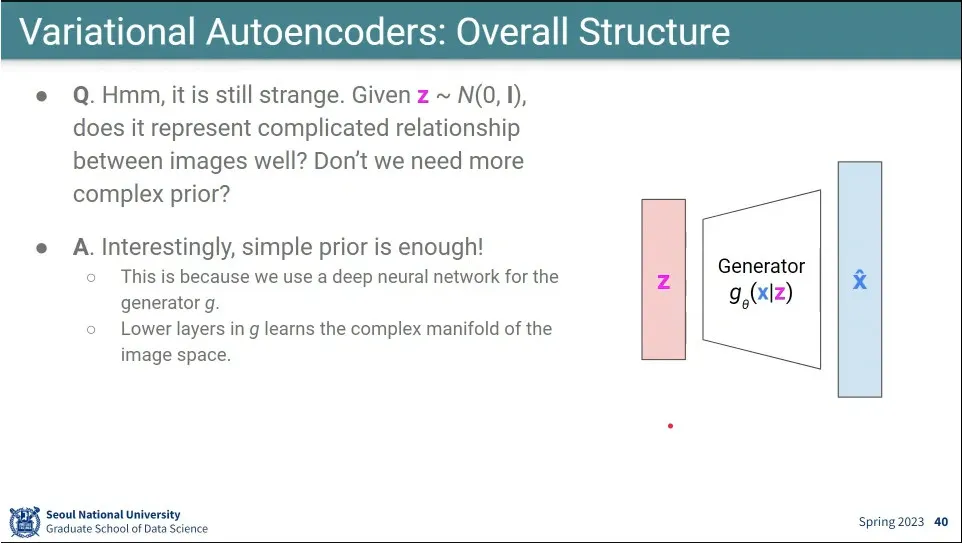
z만으로 복잡한 이미지 관계를 표현할 수 있을까? → 실제로 잘 됨.
◦
Generator가 처리해 주는 것으로 추측.
•
사례
◦
해석 가능한 결과가 나옴.
•
Generative 모델을 수학적으로 만든 모델
•
해석 가능한 latent space가 나오고, 다른 task에 쓰는데 유용하다는 장점이 있음.
•
approximate 텀이 있어서 성능이 떨어질 수 있음.
•
GAN보다 이미지 퀄리티가 좋지 않음.