•
이전에 들었던 유사한 부분이 많기 때문에 간략히 정리. 상세 내용은 아래 페이지 참조
•
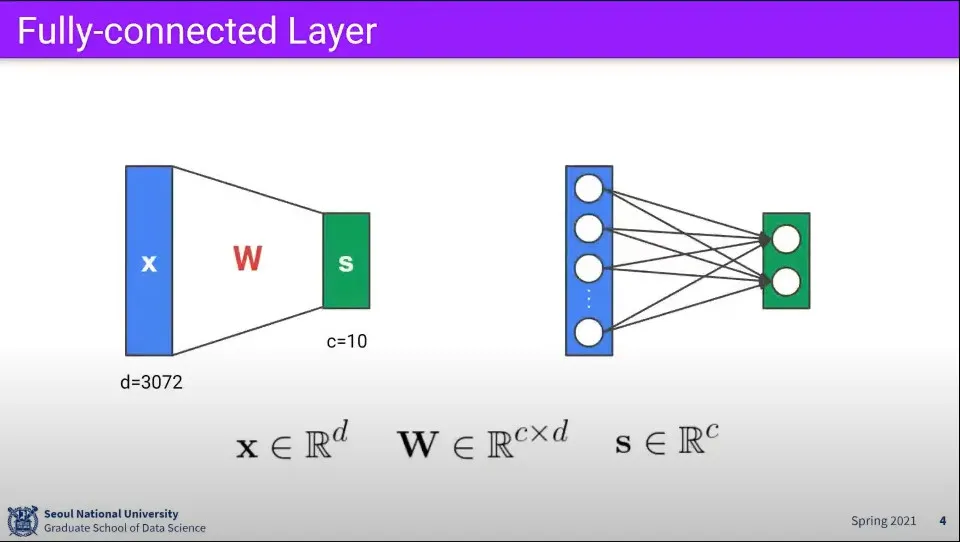
지금까지 본 것은 Fully-connected Layer
•
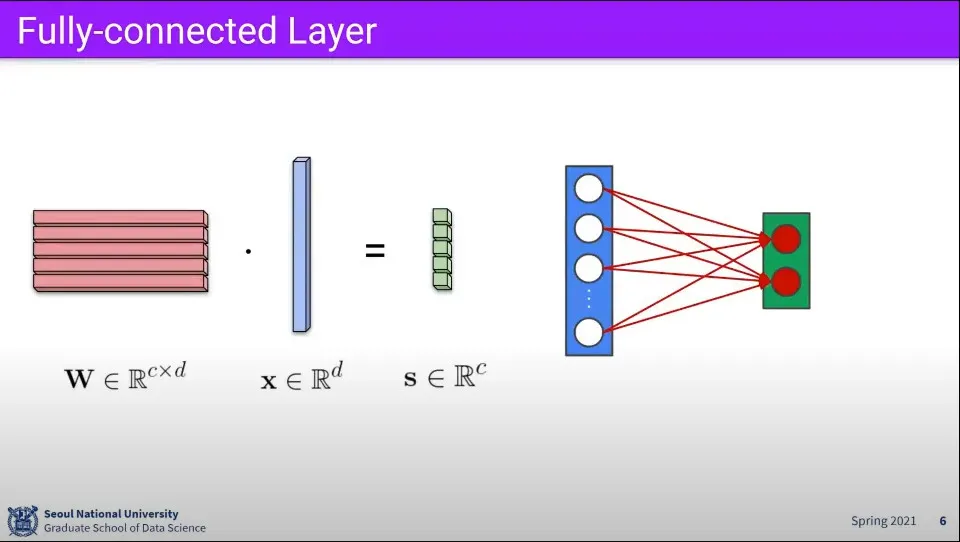
Fully-connected에서 연산은 위와 같다.
•
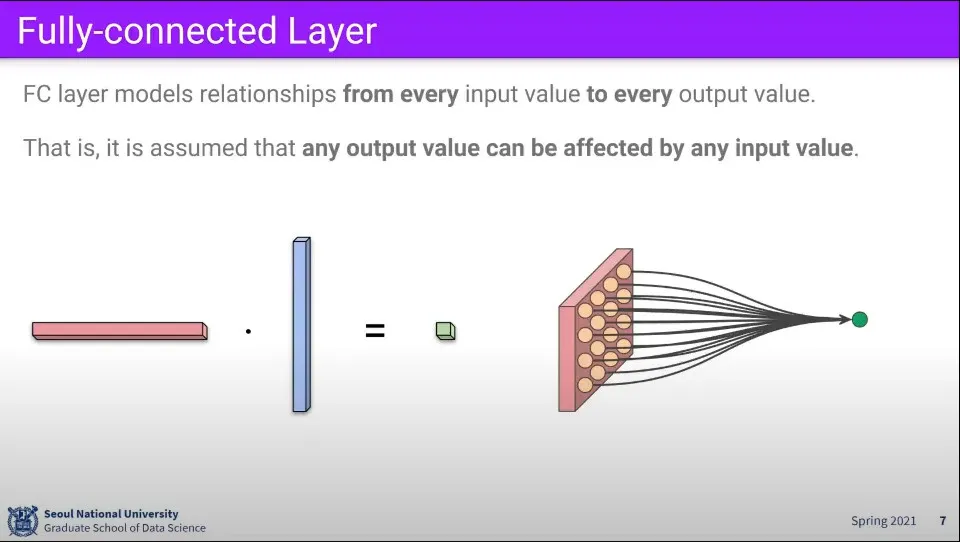
이것은 사실 위와 같이 생각할 수 있다. 이미지의 각 픽셀들의 모여서 하나의 결과를 만듦
•
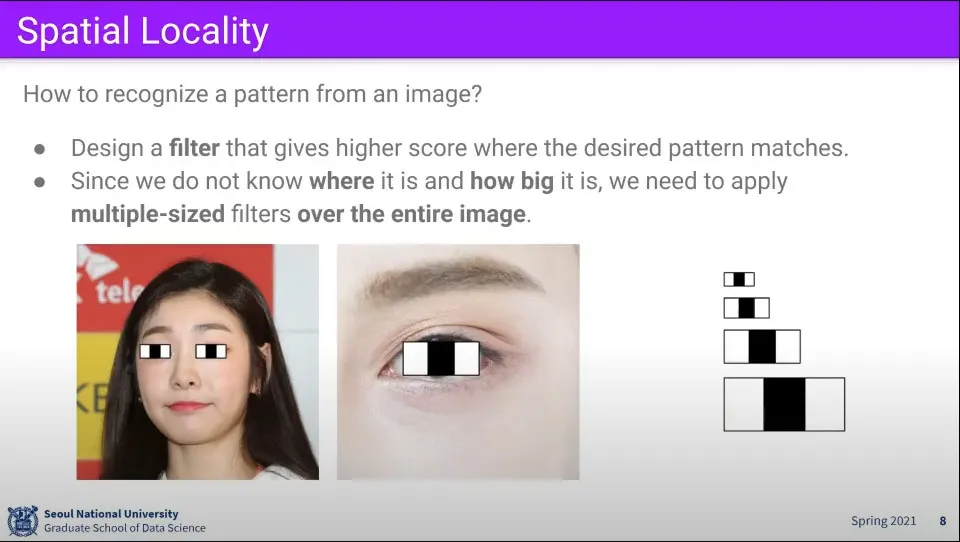
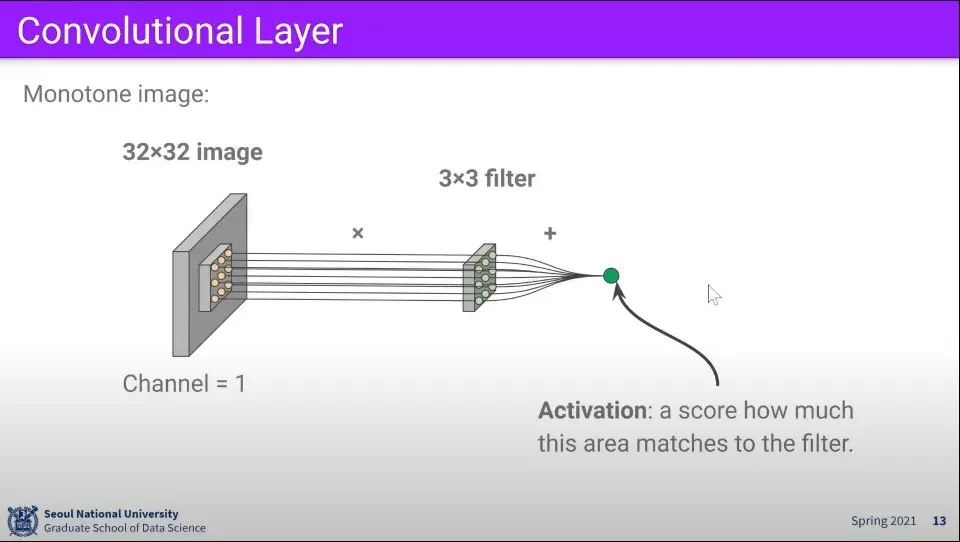
이미지에서 눈을 인식하려고 한다면, 눈에 해당하는 어떠한 필터가 있고, 그것을 이미지 내에서 찾는 것으로 생각 할 수 있다.
•
이를 위한 코드는 위와 같이 생각할 수 있다.
◦
필터를 이미지 위에서 한 칸씩 돌면서 매칭되는 것을 찾음
•
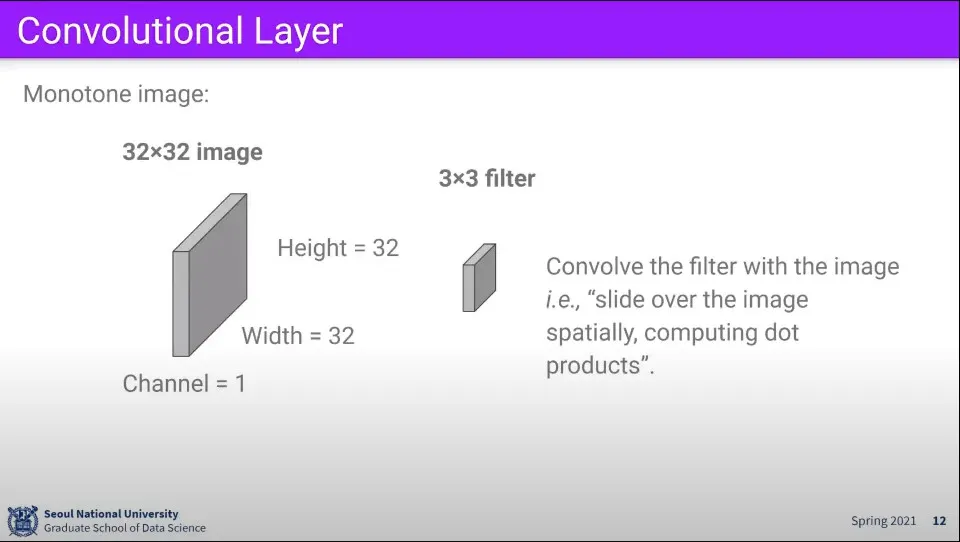
Convolution Layer는 filter와 이미지를 계산해서 결과를 구하는 것
•
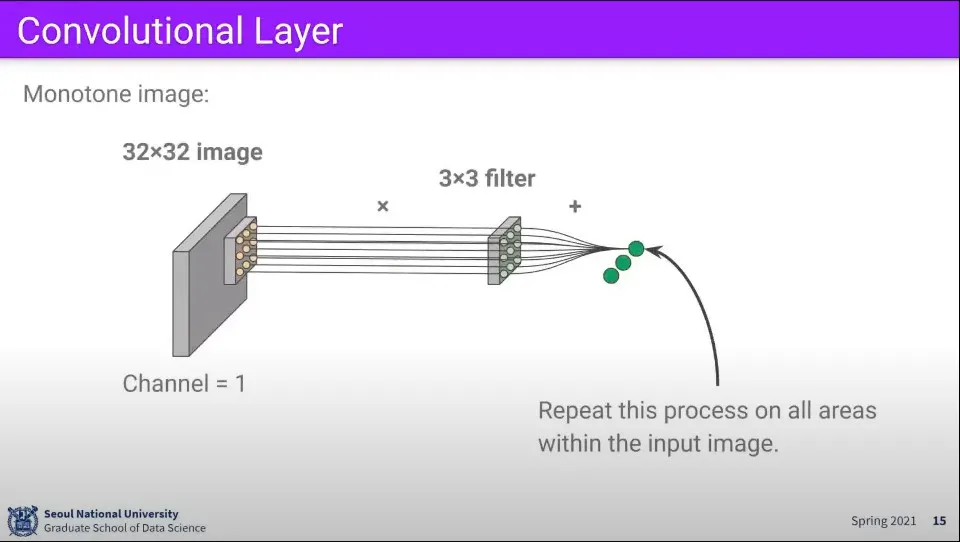
이미지 위에서 한 칸씩 움직이면서 계산을 하면 위와 같이 결과를 구할 수 있다.
•
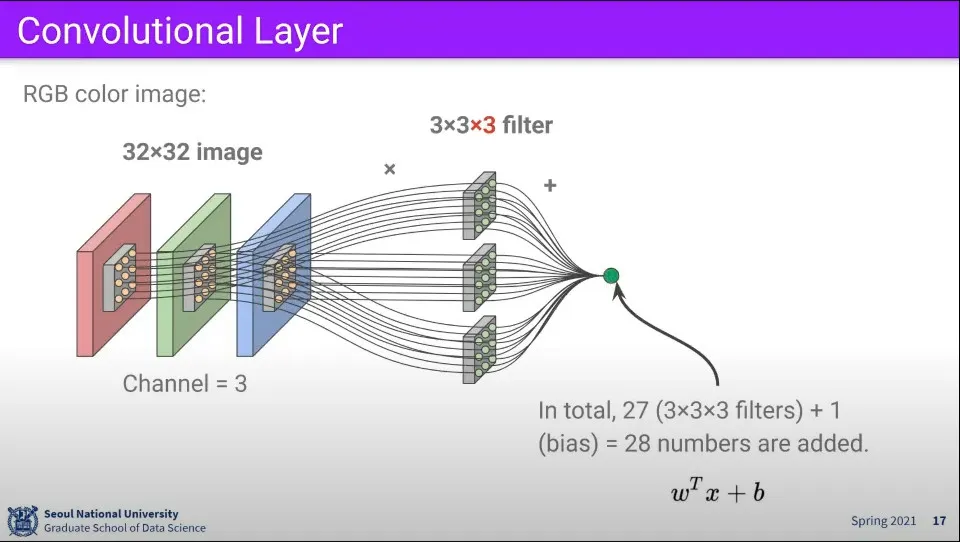
만일 RGB 3개의 채널이 있다면 필터도 3개를 사용하면 된다.
•
각 채널별로 필터와 곱해서 결과를 구한다.
•
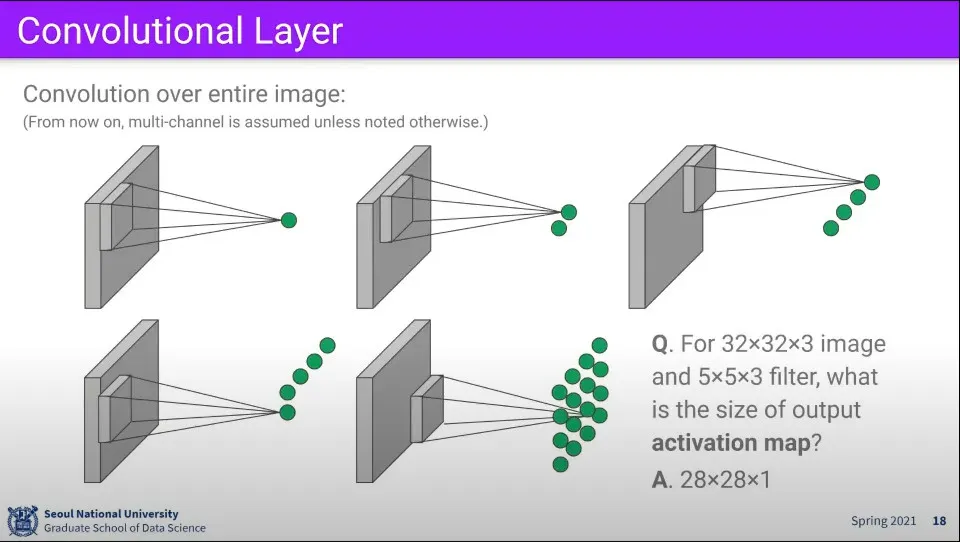
필터를 이미지 위에서 한칸씩 움직이면서 계산을 하면 위와 같은 결과를 얻을 수 있다.
◦
32x32x3 이미지에 5x5x3 필터를 이용하면 28x28x1 크기의 결과를 얻을 수 있다.
•
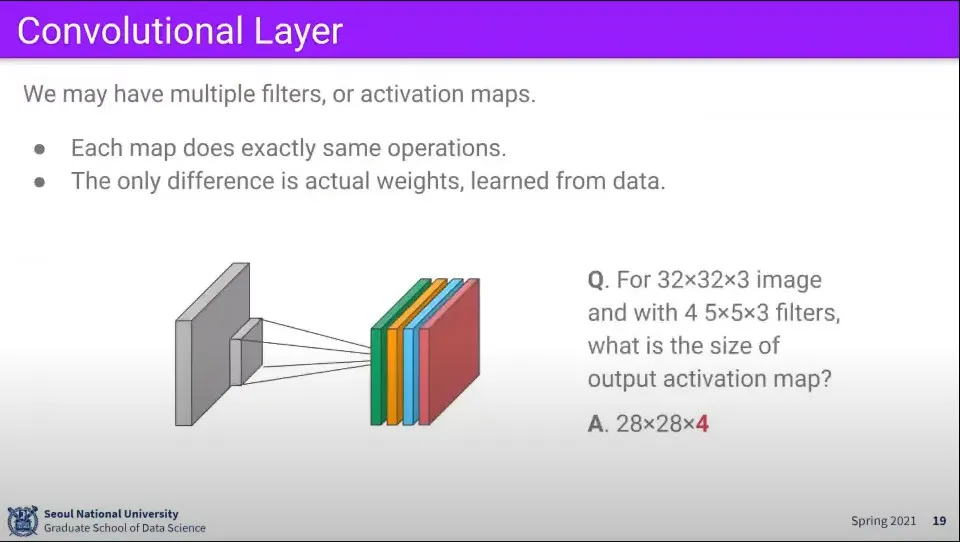
만일 인식하고자 하는 클래스가 여러개라면 마찬가지로 그 개수만큼 연산을 해주면 된다.
◦
위와 같은 조건에서 filter가 4개였다면 최종 결과는 28x28x4의 크기가 된다.’
•
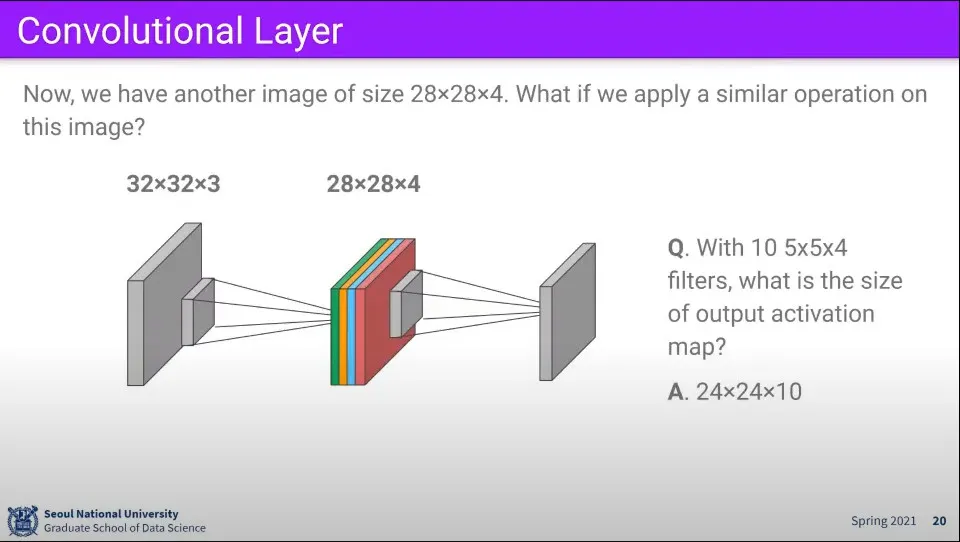
그렇게 만든 filter에 대해 다시 filter를 적용해서 연산할 수 있다.
◦
28x28x4의 filter에 대해 5x5x4 필터 10개를 다시 적용하면 그 결과는 24x24x10의 크기가 된다.
•
filter에 대해 filter를 적용하는 것은 Low-level feature로부터 더 상위 level의 feature를 뽑고, 거기서 다시 더 상위 level의 feature를 뽑기 위함이다. 이것이 반복되는 것이 deep learning이다.
•
위와 같은 방법에서 문제가 되는 부분이 있다.
◦
filter를 계속 쓰면 activation map의 크기는 점점 작아지는데 나중에 가면 이미지가 사라질 수도 있다.
◦
이미지 해상도가 높을 때 연산량이 너무 많다.
•
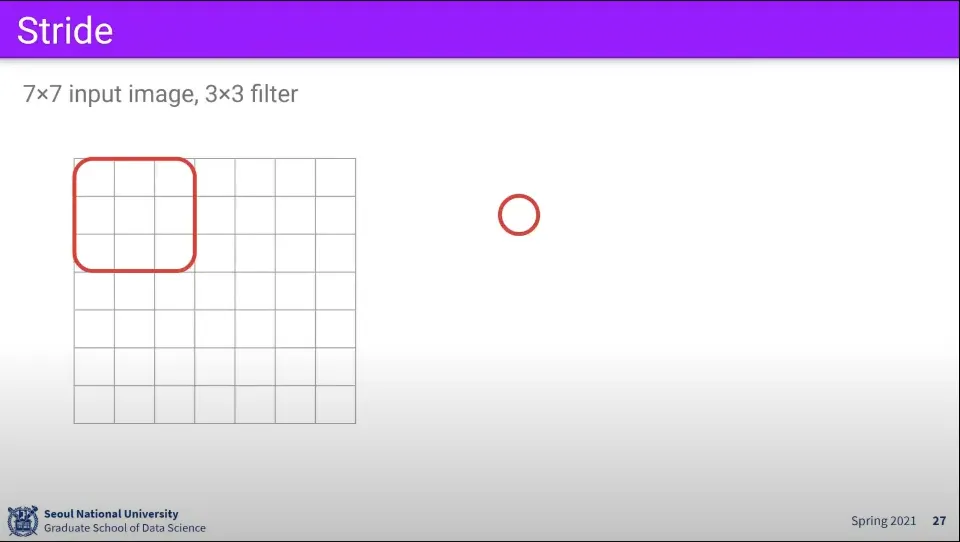
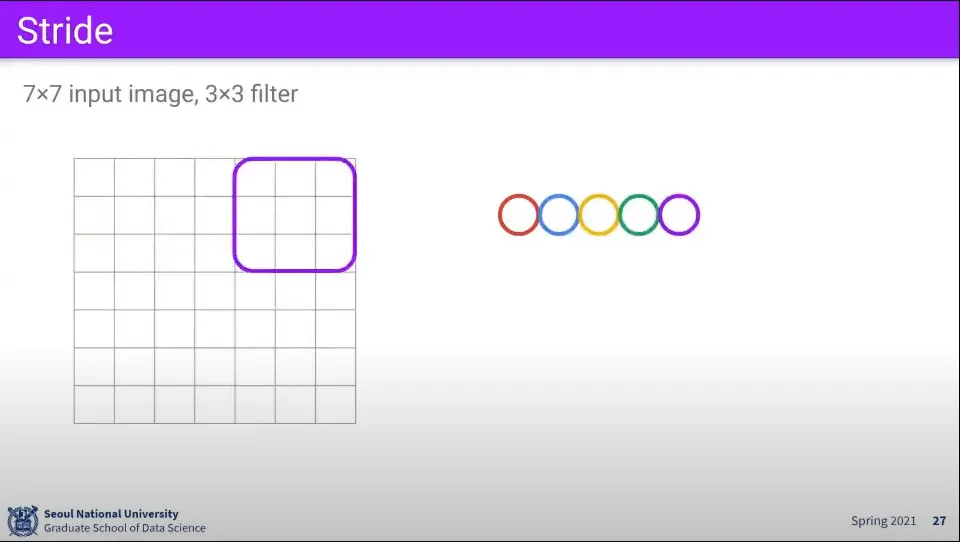
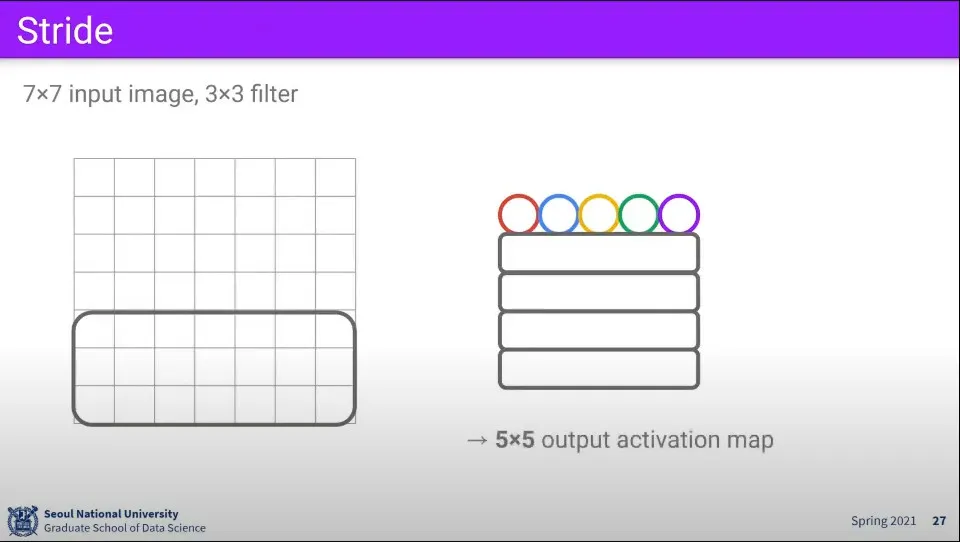
7x7 이미지에 대해 3x3 filter를 적용하면 위와 같이 계산되어 최종적으로 5x5 크기의 activation map이 만들어진다.
•
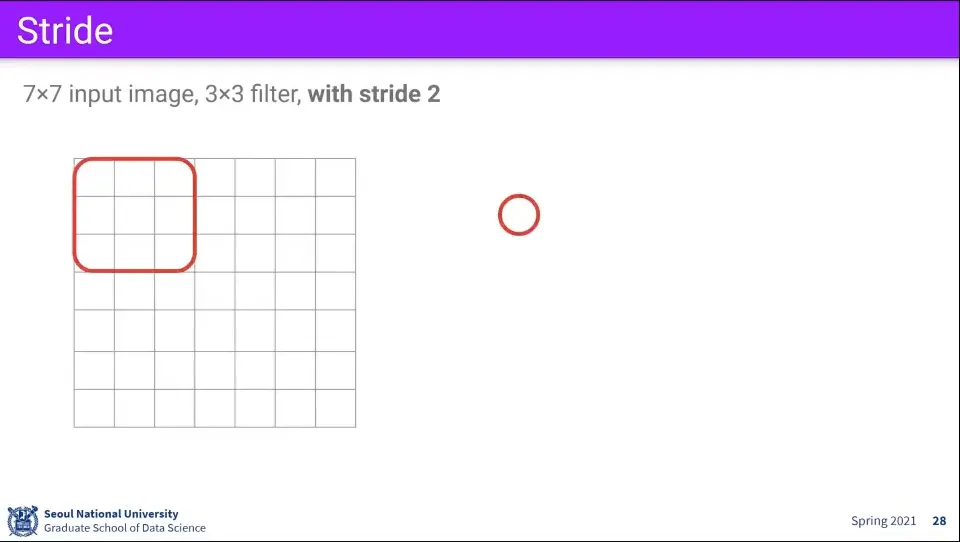
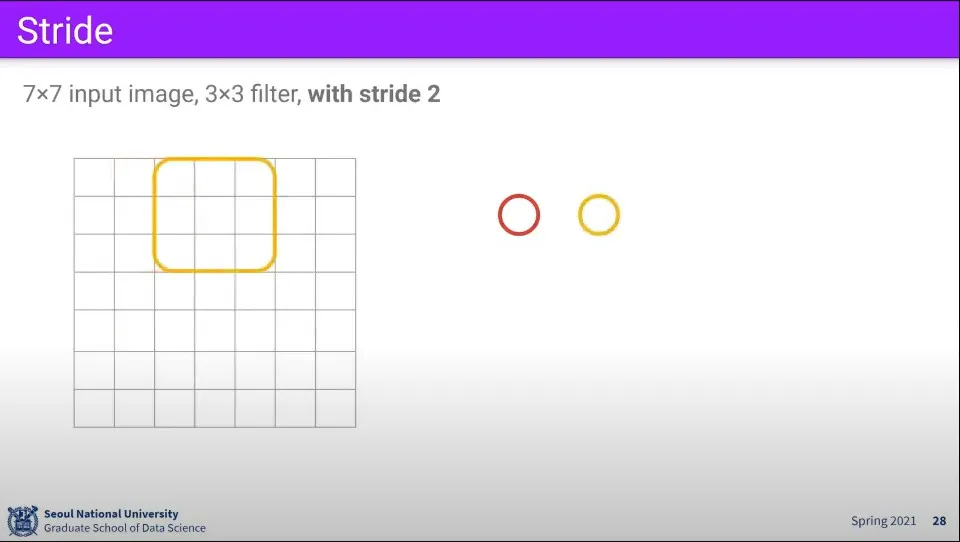
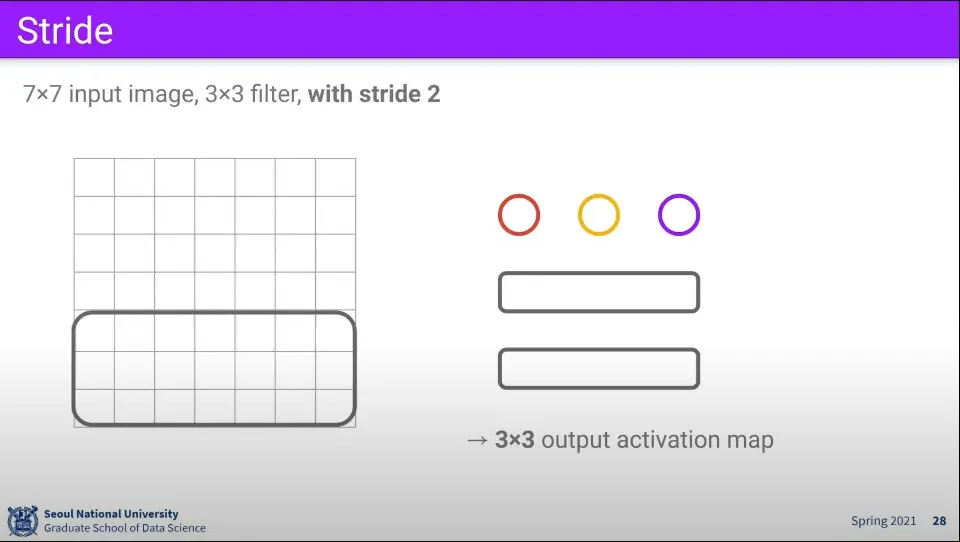
같은 조건에 대해 만일 filter를 1칸씩 움직이지 않고 2칸씩 움직인다면 최종 결과는 3x3 크기가 된다.
◦
이때 filter가 움직이는 크기를 stride라고 한다.
•
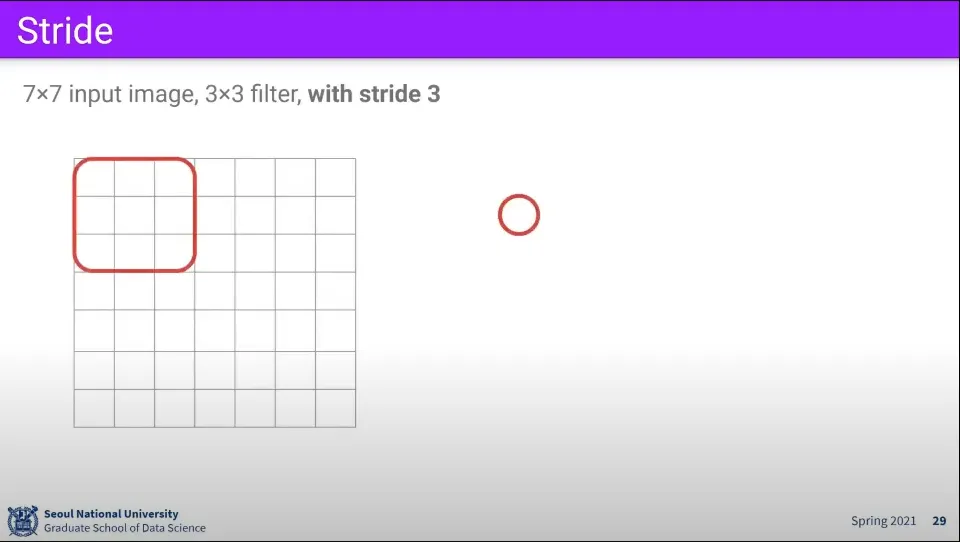
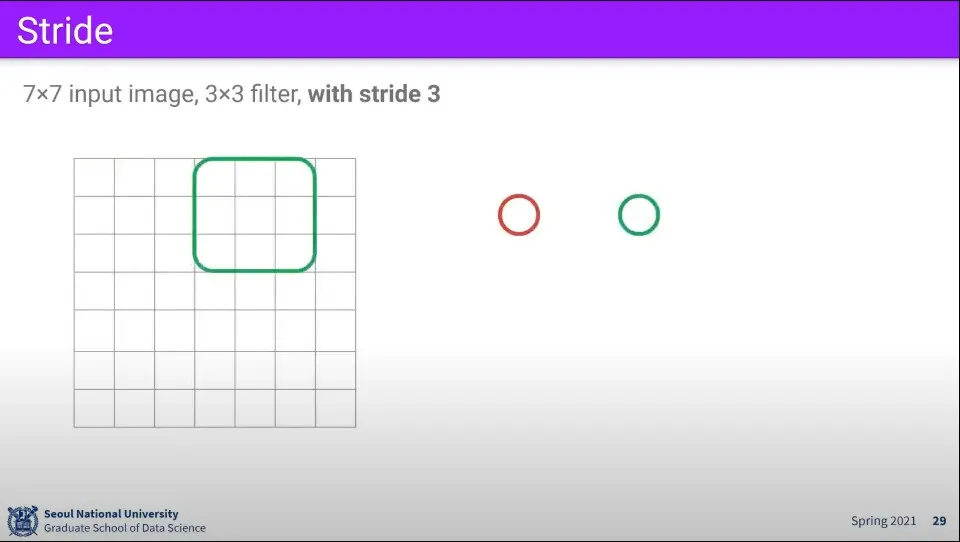
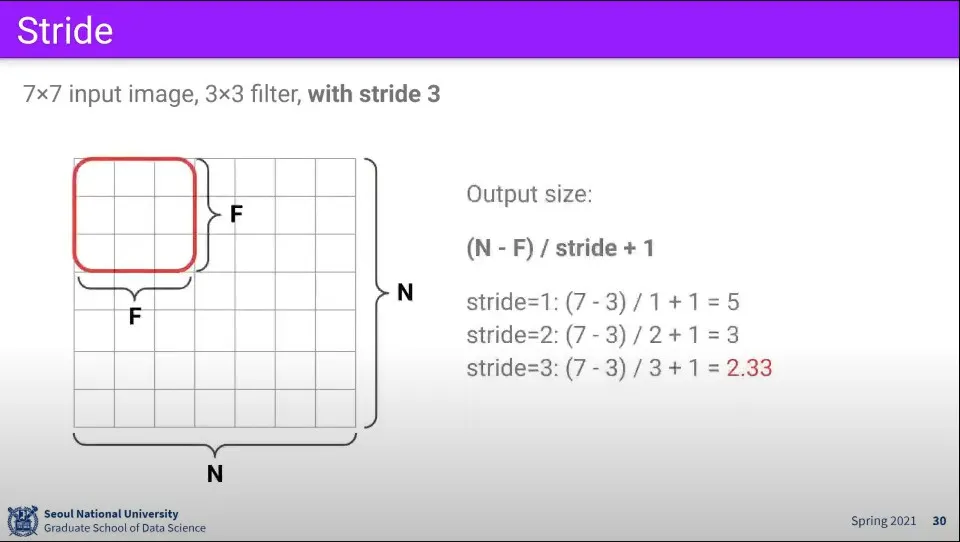
그런데 만일 같은 상황에서 stride를 3으로 올리면 어떻게 될까? 이 경우 더 움직일 수 없는 상황이 발생한다.
•
이것이 안 되는 이유는 위와 같이 3칸씩 움직일 때 자연수로 떨어지지 않기 때문이다.
•
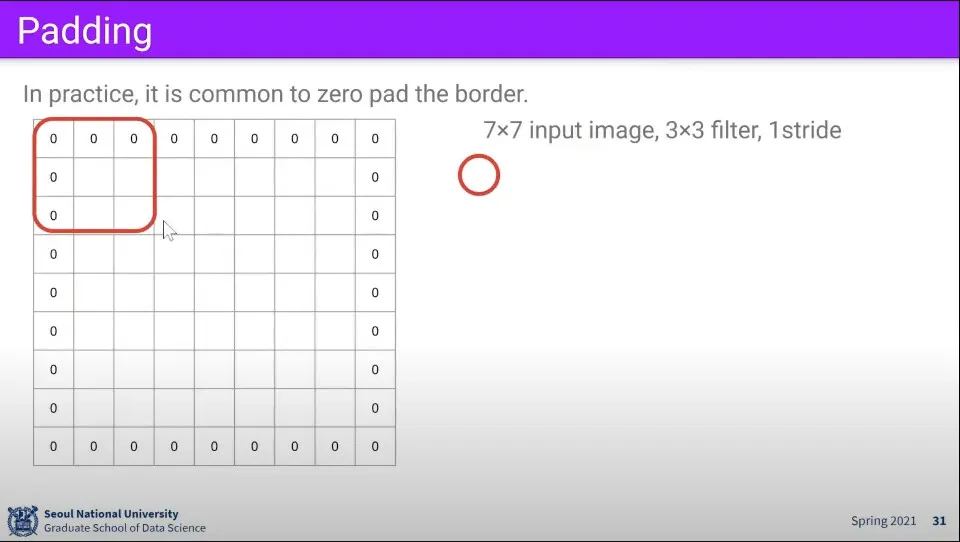
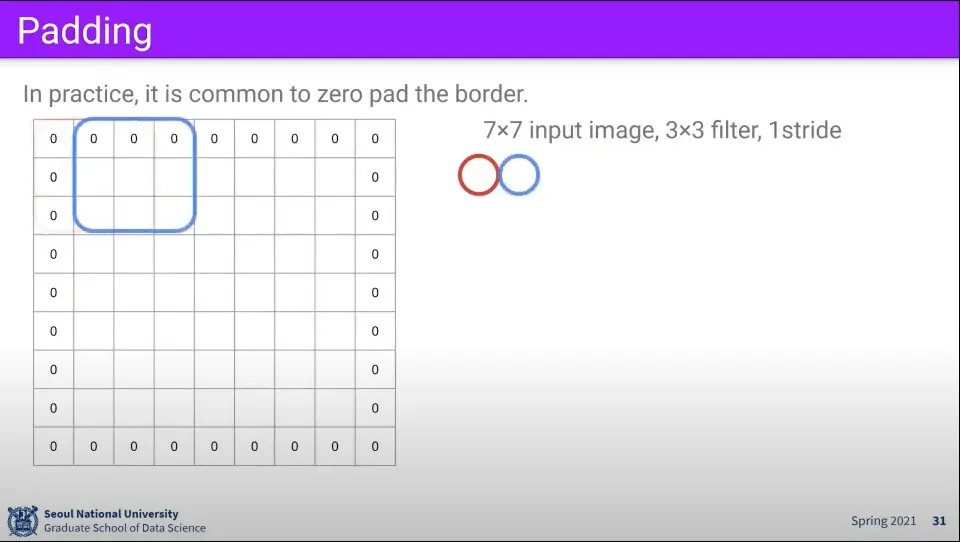
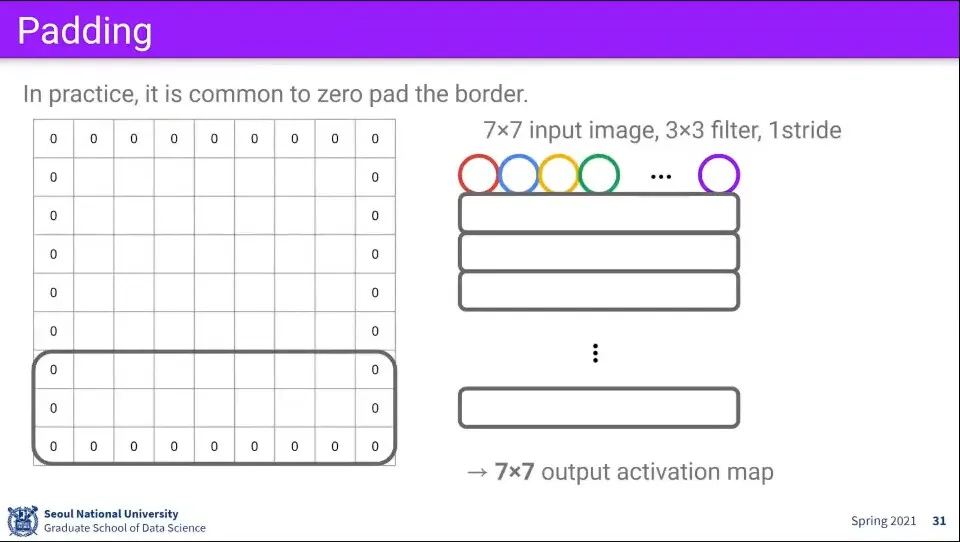
만일 이런 상황에서 이미지 바깥으로 0으로 채워서 1줄씩 추가해주면 결과가 위와 같이 만들어진다.
◦
이때 이미지 바깥으로 0으로 채우는 것을 padding이라고 한다.
◦
이것을 이용하면 stride가 안 맞는 문제를 해결할 수 있다.
•
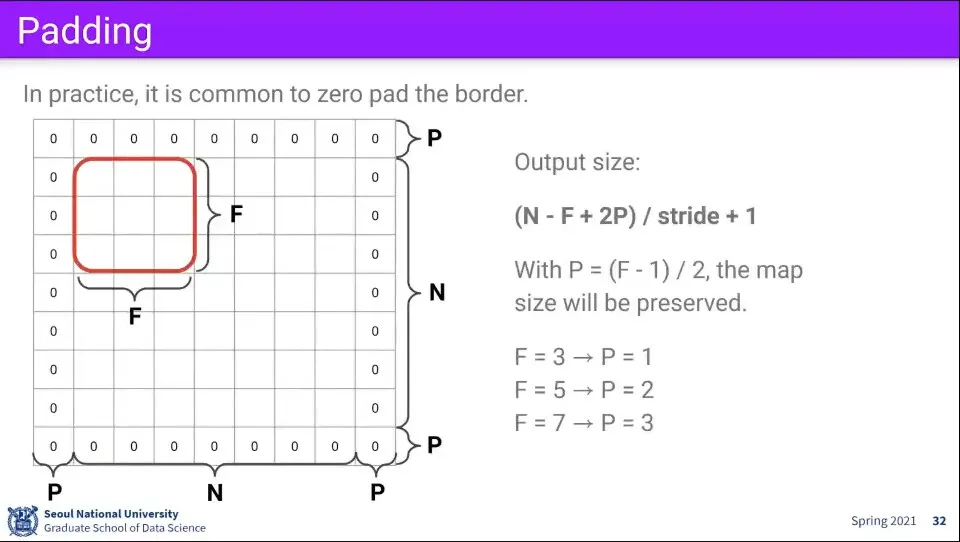
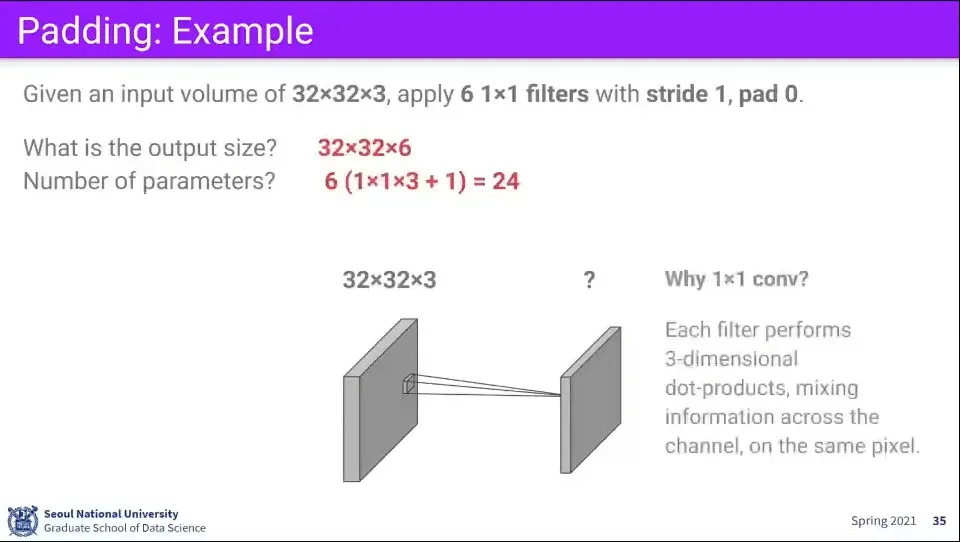
padding을 고려해서 output을 계산하는 공식을 위와 같이 정리할 수 있다.
•
패딩을 이용하면 filter에 의해 output 크기가 줄어드는 문제를 해결할 수 있다.
•
추가로 stride를 이용하면 연산량도 줄일 수 있다.
•
위와 같은 조건에서 Convolution 맵의 파라미터 수는 760개가 되는데 이것은 fully-connected일 때 3100만개의 파라미터에 비해 훨씬 적은 수의 연산량을 가질 수 있다.
•
만일 Filter의 크기를 1x1으로 사용한다면 어떻게 될까? 이 경우 전체 이미지의 차원을 조정하는 효과가 발생한다.
◦
공간적인 정보는 건드리지 않고 차원만 수정하고 싶을 때 이것을 사용한다.
•
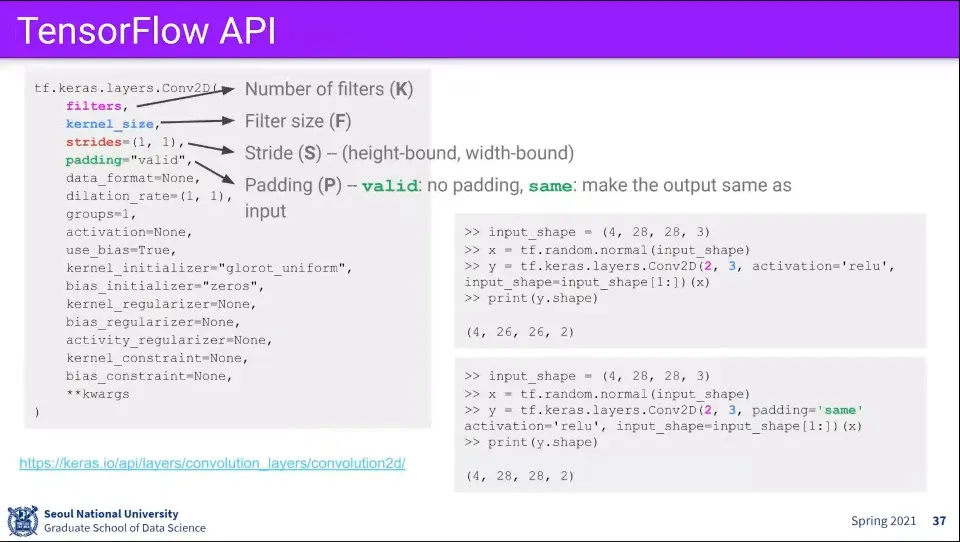
Convolution Layer의 파라미터들은 위와 같다.
◦
Filter의 개수
◦
Filter의 크기
◦
Stride 크기
◦
Padding 크기
•
이 파라미터들을 이용하면 output의 크기(W, H)와 파라미터 수를 위와 같이 계산할 수 있다.
•
텐서플로에서의 Conv Layer 예시
•
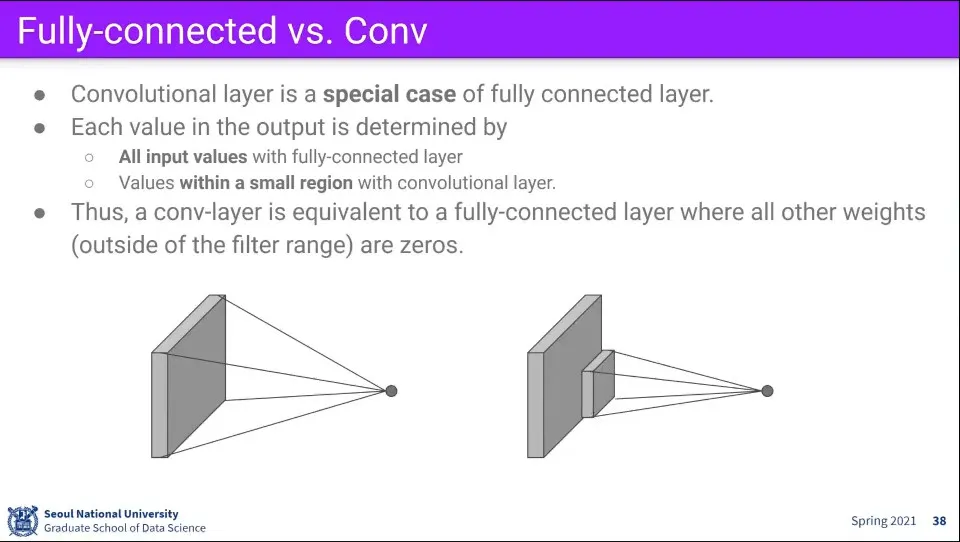
Fully-connected의 특수한 케이스가 Conv 레이어이다.
◦
또한 Conv 레이어의 특수한 케이스가 Fully-connected 레이어가 될 수 있음
•
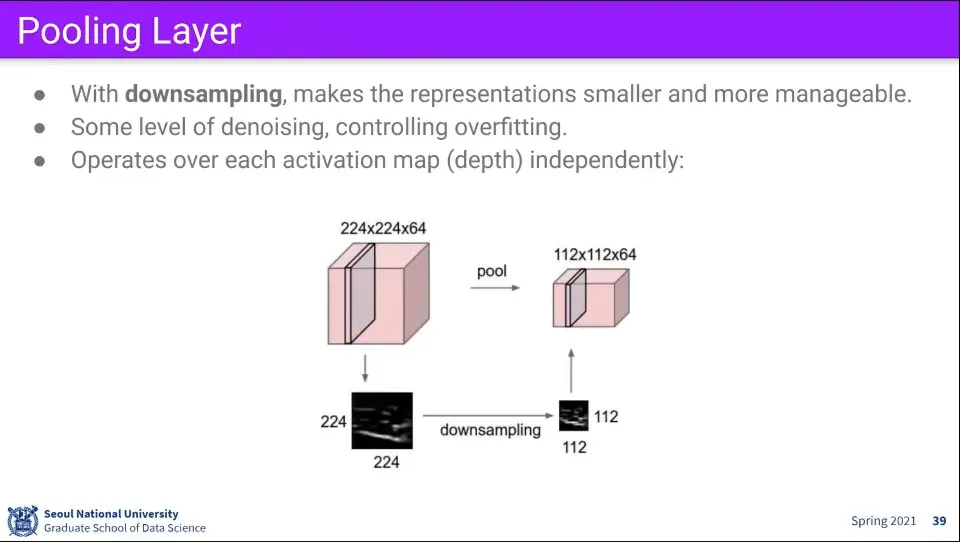
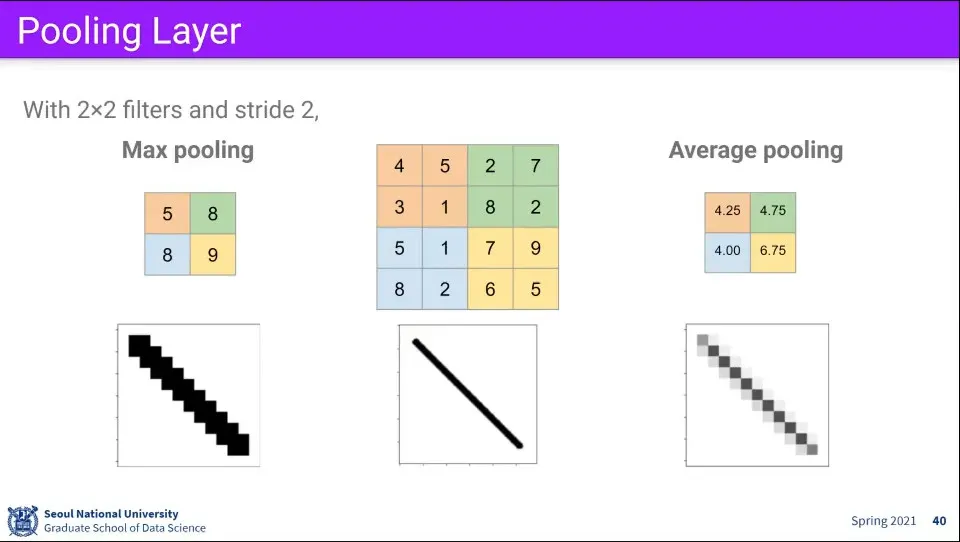
Pooling layer는 이미지를 downsampling 하는 레이어이다.
•
픽셀 레벨에서는 노이즈가 있기도 하고 픽셀 몇 개 정도는 학습에 큰 영향을 주지 않고, 사이즈를 줄이면 연산량도 줄일 수 있고, overfitting이 발생하는 것을 방지하는 효과도 있다.
•
Pooling layer는 Max 값을 취하는 방식이나 Average 값을 취하는 방식이 있다.
•
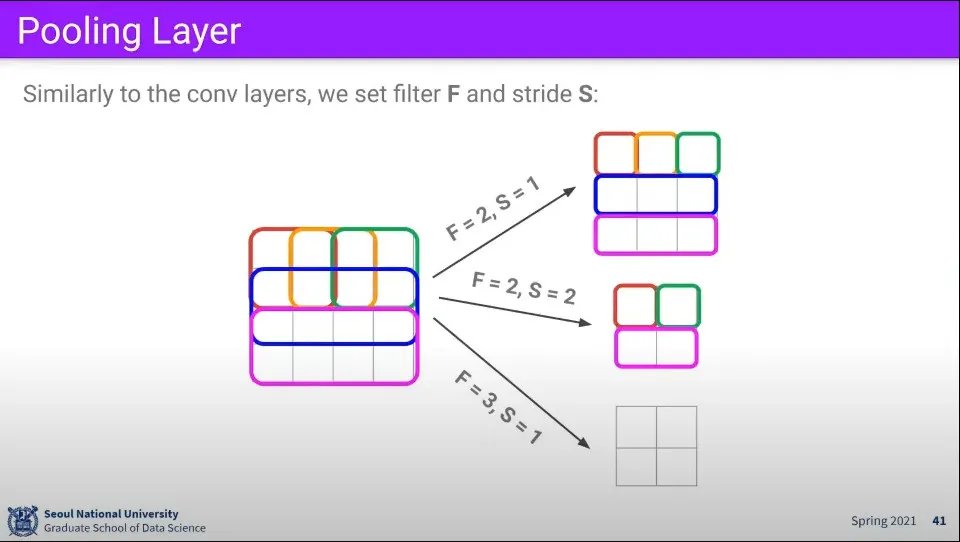
Pooling 레이어에서 Filter의 크기와 Stride 크기를 조절해서 결과를 조절할 수 있다.
•
Pooling 레이어의 파라미터를 이용해서 output의 크기를 계산할 수 있다.
•
Pooling 레이어는 이미지 크기를 조절하는 것이므로 학습은 이루어지지 않는다.
•
최근 경향은 Pooling Layer를 쓰지 않아도 된다는 쪽으로 가고 있음. Conv Layer의 파라미터만 잘 설계해도 같거나 더 좋은 효과를 얻을 수 있음