1 Introduction
카메라는 computer vision에서 가장 필수적인 도구 중 하나이다. 이것은 우리를 둘러싼 세계를 기록할 수 있고 그 결과물인 사진을 다양한 응용을 위해 사용할 수 있는 메커니즘이다. 따라서 입문 computer vision에서 우리가 물어야 할 한 가지 질문은 이것이다. ‘카메라를 어떻게 모델링할 수 있는가?’
2 Pinhole cameras
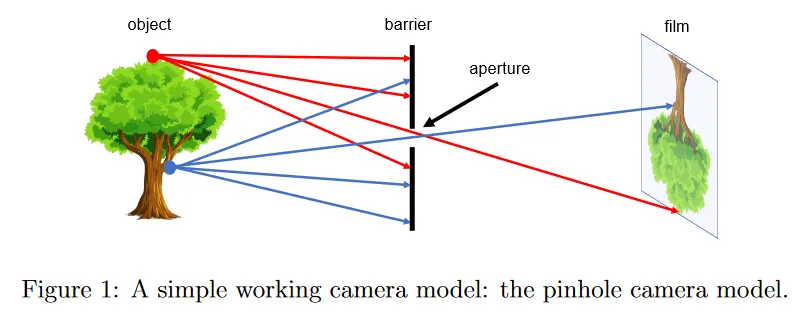
3d 공간에서 객체나 장면의 이미지를 기록할 수 있는 간단한 카메라 시스템을 설계해 보자. 이 카메라 시스템은 3d 객체와 photographic 필름 또는 센서 사이의 작은 aperture(구멍)이 있는 barrier를 두어 설계할 수 있다. 그림 1과 같이 3d 객체의 각 점에서 바깥 방향으로 여러 light ray를 방출한다. barrier가 없다면 필름의 모든 점에 3d 객체의 모든 점에서 방출된 light ray이 영향을 미칠 것이다. 그러나 이 barrier 때문에 이러한 light ray 중 단 하나 (또는 적은)만 구멍을 통과하여 필름을 때린다. 그러므로 3d 객체의 점과 필름 사이에 one-to-one 매핑을 설정할 수 있다. 그 결과 필름에는 이 매핑을 통해 3d 객체의 ‘image’가 노출된다. 이러한 간단한 모델을 pinhole camera model이라 한다.
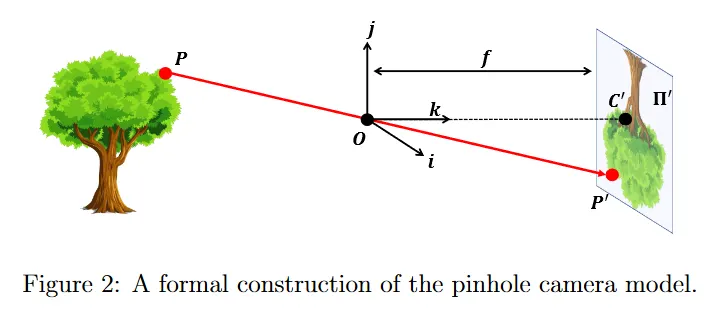
pinhole 카메라의 더 형식적인 구성은 그림 2에 나와 있다. 이 구성에서 필름은 일반적으로 image 또는 retinal(망막) plane이라고 불린다. 구멍은 pinhole 또는 카메라의 중심을 의미한다. 이미지 평면과 pinhole 사이의 거리를 focal(초점) length 라고 한다. 때때로 retinal plane이 와 3d 객체 사이에 로부터 거리 에 놓이기도 한다. 이 경우에 이것을 virtual image 또는 virtual retinal plane이라 부른다. 이미지 평면에서 투영된 객체와 virtual image plane에서 객체의 이미지는 scale (similarity) transformation을 제외하면 identical이다.
이제 어떻게 pinhole 카메라를 사용할 수 있을까? 을 pinhole 카메라에 보이는 어떤 3d 객체의 점이라고 하자. 는 이미지 평면 에 map 또는 project 되어 점 가 된다. 유사하게 pinhole 자체도 이미지 평면에 투영되어 새로운 점 가 생긴다.
여기서 pinhole 를 중심으로 좌표계 을 정의할 수 있다. 이때 축 가 이미지 평면에 perpendicular(수직)이고 평면을 향한다. 이 좌표계를 종종 camera reference system 또는 camera coordinate system이라 부른다. 와 에 의해 정의되는 직선을 카메라 시스템의 optical axis라고 한다.
점 가 이미지 평면 에 대한 3d 점 의 projection에서 유도된다는 점을 떠올려라. 그러므로 3d 점 와 이미지 평면 점 사이의 관계를 유도할 수 있으면 3d 세계가 pinhole 카메라에 의해 얻어진 이미지에 어떻게 imprints(각인) 되는지 이해할 수 있다. 삼각형 이 와 와 에 의해 형성된 삼각형이 유사함에 주목하라. 그러므로 삼각형의 유사도 법칙을 사용하여 다음을 발견할 수 있다.
이 pinhole 모델에서 우리가 하는 하나의 큰 가정은 구멍이 단일 점이라는 것이다. 그러나 대부분의 현실세계에서 구멍이 무한히 작다고 가정할 수 없다. 따라서 구멍의 크기를 변경하면 어떻게 될까?
구멍 크기가 증가하면 barrier를 통과하는 light ray의 수도 증가한다. 더 많은 light ray가 통과하면 필름에 대한 각 점에 3d 공간에서 여러 점에서 온 light ray에 의해 영향 받아 이미지가 blurring 된다. 구멍을 가능한 작게 만들고 싶겠지만, 구멍 크기가 더 작아지면 통과하는 light ray의 수가 줄어들어 이미지가 crisper(선명)하지만 어두워 진다. 그러므로 우리는 pinhole 공식에서 제기되는 근본적인 문제에 도달했다. ‘crisp(선명)하고 bright 이미지를 촬영할 수 있는 카메라를 개발할 수 있는가?’
3 Cameras and lenses
현대 카메라에서는 빛을 focus 또는 disperse(분산) 할 수 있는 장치인 lens를 사용하여 crispness와 brightness 사이의 충돌을 mitigated(완화)할 수 있다. pinhole 대신 properly(적절한) 위치와 크기의 렌즈를 사용하면 다음 속성을 만족한다.
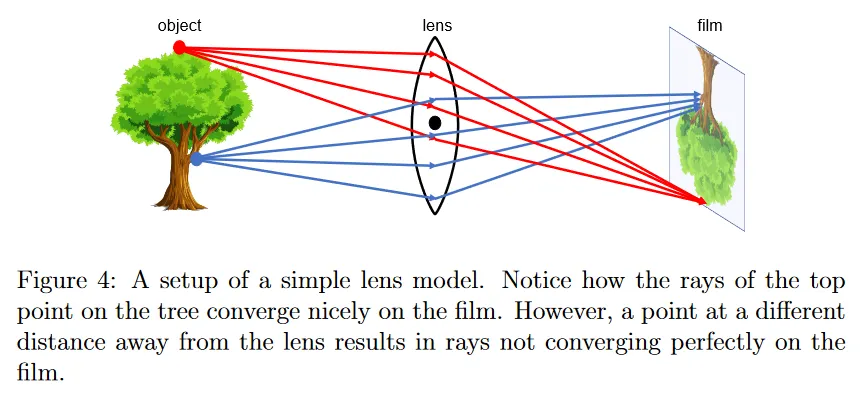
어떤 점 에서 방출되는 모든 light ray는 렌즈에 의해 refracted(굴절)되어 이미지 평면에서 단일 점 에 수렴한다. 따라서 작은 구멍 때문에 대부분의 light ray가 차단되는 문제가 제거된다(그림 4). 그러나 이 속성은 모든 3d 점이 아니라 어떤 특정한 점 에 대해서만 성립하는 것에 유의하라. 보다 이미지 평면에서 더 멀거나 가까운 또 다른 점 를 생각해 보면, 이미지 평면에 투영된 의 이미지는 blurred 또는 focus out일 수 있다. 따라서 렌즈는 객체가 ‘in focus’인 특정한 거리를 갖는다. 이 속성은 또한 photography와 computer graphics에서 depth of field라는 개념과 연관된다. 이것은 카메라가 깨끗한 이미지를 얻을 수 있는 유효 범위를 나타낸다.
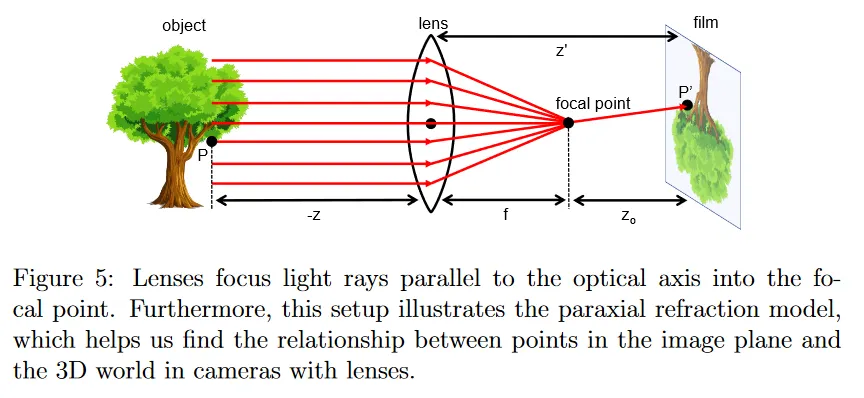
카메라 렌즈는 또 다른 흥미로운 속성을 갖는다. optical axis에서 평행으로 이동하는 모든 light ray가 focal point라 하는 하나의 점에 모인다(그림 5). focal point와 렌즈의 중심 사이의 거리를 일반적으로 focal length 라고 한다.
게다가 렌즈의 중심을 통과하는 light ray는 deviated(굴절)되지 않는 한다. 따라서 3d 공간의 점 와 이미지 평면에서 해당하는 점 사이의 관계를 pinhole 모델과 유사하게 구성할 수 있다.
이 모델에 대한 유도는 이 수업의 범위를 벗어난다. 그러나 pinhole 모델에서 인 반면 lens-based 모델에서 임에 유의하라. 또한 이 유도가 paraxial(근축) 또는 ‘thin lens’ 가정의 이점을 취하기 때문에 이것을 paraxial refraction model이라 한다.
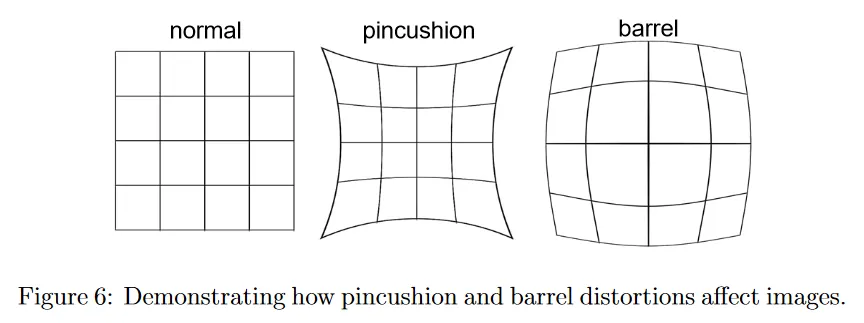
paraxial refraction 모델이 thin lens 가정을 사용하여 근사하기 때문에 많은 aberration(수차)가 발생할 수 있다. 가장 일반적인 것은 radial distortion(왜곡)이라 하는데, optical axis에서의 거리에 따라 image magnification(배율)을 감소하거나 증가하게 만든다. 우리는 magnification이 증가할 때, pincushion distortion으로 분류하고 magnification이 감소할 때 barrel distortion이라 분류한다. Radial distortion은 렌즈의 서로 다른 점이 서로 다른 focal length를 갖는다는 사실에 의해 발생한다.
4 Going to digital image space
이 섹션에서 3d 공간에서 우리가 알고 있는 디지털 이미지로의 투영을 모델링할 때 고려해야 하는 파라미터의 세부사항을 논의한다. 모든 결과는 pinhole 모델을 사용하여 유도되지만 paraxial refraction 모델에 대해서도 유지된다.
앞서 논의한 것처럼 3d 공간에서 점 는 이미지 평면 의 2d 점 으로 매핑 (또는 투영) 될 수 있다. 이 매핑을 projective transformation이라 부른다. 그러나 3d 점의 이미지 평면 투영하는 것은 실제 디지털 이미지에 직접적으로 대응하지 않는데, 그 이유는 다음과 같다. 첫째, 디지털 이미지에서 점은 일반적으로 이미지 평면과 다른 reference system(기준계)를 사용한다. 둘째, 디지털 이미지는 이산 픽셀로 나뉘지만, 이미지 평면 상의 점은 연속이다. 마지막으로 물리적 센서에 의해 왜곡과 같은 비선형성이 매핑에 대한 도입될 수 있다. 이러한 차이를 고려하기 위해 3d 세계의 임의의 점을 픽셀 좌표에 매핑하는 몇 가지 추가적인 변환을 소개한다.
4.1 The Camera Matrix Model and Homogeneous Coordinates
4.1.1 Introduction to the Camera Matrix Model
카메라 행렬 모델은 월드 점 가 이미지 좌표 에 어떻게 매핑되는데 영향을 미치는 중요한 파라미터의 집합을 설명한다. 이름에서 알 수 있듯이 이러한 파라미터들은 행렬 형태로 표현된다. 우선 이런 파라미터 중 일부를 소개한다.
첫 번째 파라미터 와 는 이미지 평면과 디지털 이미지 좌표 사이의 translation(평행이동) 차이를 설명한다. 이미지 평면 좌표의 원점 는 축은 이미지 평면과 교차하는 이미지 중심에 있는 반면, 디지털 이미지 좌표의 원점은 일반적으로 이미지의 왼쪽 아래 모서리에 있다. 따라서 이미지 평면의 2d 점과 이미지의 2d 점은 translation vector 만큼 offset 된다. 이 좌표 체계의 변환을 수용하기 위해 다음과 같이 매핑한다.
두 번째로 고려해야 할 효과는 디지털 이미지의 점은 픽셀로 표현되지만 이미지 평면의 점은 물리적 측정 단위(예: centimeters)로 표현된다는 것이다. 이 단위의 변화를 수용하기 위해 우리는 2가지 새로운 파라미터 와 을 도입한다. 이 파라미터들의 단위는 과 같은 것이되며, 이미지 평면의 2개 축에서 단위의 변화에 해당한다. 와 이 다를 수 있는 이유는 픽셀의 aspect ratio(종횡비)가 1로 보장되지 않기 때문이다. 만일 인 경우 카메라가 square pixels을 가졌다고 말한다. 우리는 이전 매핑을 다음처럼 조정한다.
에서 이 투영을 나타내는 더 좋은 방법은 없는가? 투영이 선형 변환이면 행렬과 입력 벡터(이 경우에 )의 곱으로 나타낼 수 있다 . 그러나 방정식 4에서 볼 수 있듯이 이 투영 는 입력 파라미터(즉 중 하나를 나누는 연산이 있기 때문에 선형이 아니다. 그럼에도 불구하고 이 투영을 행렬-벡터 곱으로 표현하면 향후 유도에서 유용하다. 비선형임에도 우리의 변환을 행렬-벡터 곱으로 표현할 수 있을까? homogeneous 좌표계가 해법이다.
4.1.2 Homogeneous Coordinates
이 문제를 해결하는 한 가지 방법은 좌표계를 변환하는 것이다. 예컨대 새로운 좌표계를 도입하여 임의의 점 를 로 표현한다. 유사하게 임의의 점 는 이 된다. 이 증강된 공간을 homogeneous coordinated system이라 부른다. 이전에 보인 유클리드 벡터 을 homogeneous 좌표계로 변환하라면 간단히 새로운 차원에 을 추가하여 로 만들면 된다. 벡터와 그것의 homogeneous 좌표가 같은 값을 갖는 경우는 마지막 좌표가 1일 때 뿐이다. 따라서 임의의 homogeneous 좌표계 에서 유클리디안 좌표로 변환하면 가 된다. homogeneous 좌표계를 사용하여 다음과 같이 공식화 할 수 있다.
달리 명시되지 않는 한 이후로 homogeneous 좌표계에서 작업한다고 가정한다. 인덱스를 제외하므로 임의의 점 또는 이 homogeneous 좌표계로 표현된다고 가정할 수 있다. 방정식 5에서 볼 수 있듯이 3d 공간의 한 점과 그 이미지 좌표계 사이의 관계를 행렬 벡터 관계로 표현할 수 있다.
이 변환을 다음과 같이 좀 더 분해할 수 있다.
행렬 를 종종 camera matrix라고 부른다.
4.1.3 The Complete Camera Matrix Model
카메라 행렬 에는 카메라의 특성과 모델을 설명하는 중요한 파라미터 일부가 포함되어 있다. 여기에는 위에서 논의한 와 가 포함된다.
현재 이 공식에서 빠진 두 가지 파라미터는 skewness(기울기)와 distortion(왜곡)이다.
카메라 좌표계가 skewed여서 두 축 사이의 각도가 90도 보다 약간 더 크거나 작으면 이미지가 skewed라고 한다. 대부분의 카메라는 zero-skew이지만, sensor manufacturing 에러 때문에 약간의 skewness가 발생할 수 있다. skewness를 고려한 새로운 카메라 행렬 유도는 이 수업의 범위를 벗어나지만, 아래와 같이 제시할 수 있다.
우리가 이 수업에서 소개하는 대부분의 방법은 distortion 효과를 무시하므로 우리가 다루는 카메라 행렬 에는 5가지 자유도가 있다. 2개는 focal length이고, 2개는 offset이고, 1개는 skewness이다. 이 파라미터들은 총칭하여 intrinsic parameter라고 한다. 그들은 특정 카메라에 고유하고 본질적인 것으로 카메라 manufacturing 같은 필수 속성과 관련이 있다.
4.2 Extrinsic Parameters
지금까지 3d 카메라 reference system의 점 를 카메라의 intrinsic 파라미터를 행렬 형태로 표현하여 2d 이미지 평면의 점 에 매핑하는 방법을 설명했다. 그렇다면 3d 세계에 관한 정보가 다른 좌표계로 주어진다면 어떻게 해야 할까? 그렇다면 world reference system의 점을 camera reference system으로 변환하는 추가 변환이 필요하다. 이 변환은 rotation matrix 과 translation vector 로 표현된다. 따라서 world reference system 가 주어지면 카메라 좌표계를 다음처럼 계산할 수 있다.
이것을 방정식 7에서 대입하고 단순화하면 다음과 같다.
이 파라미터 과 가 외부에 있고 카메라에 의존하지 않기 때문에 extrinsic parameters라고 한다.
이로써 임의의 월드 reference system에서 3d 점 를 이미지 평면으로 매핑하는 과정이 완성된다. 요약하자면 전체 투영 행렬 이 위에서 소개한 2가지 유형의 파라미터, 즉 intrinsic과 extrinsic 파라미터로 구성된다. 카메라 행렬 에 포함된 모든 파라미터들은 카메라의 유형이 변화함에 따라 변하는 intrinsic 파라미터이고, extrinsic 파라미터는 카메라가 제작 방식과 무관한 회전과 평행이동을 포함한다. 전체적으로 투영 행렬 이 11개의 자유도를 가지는 것을 볼 수 있다. 5개는 intrinsic 카메라 행렬에서 오고, 3개는 extrinsic rotation에서 오고, 3개는 extrinsic translation에서 온다.
5 Camera Calibration
실제 3d 세계에서 디지털 이미지로의 변환을 정확히 알기 위해서는 카메라의 intrinsic 파라미터에 대한 많은 사전 지식이 필요 하다. 임의의 카메라가 주어지면 이러한 파라미터에 접근할 수도 있고 안 할 수도 있다. 그러나 카메라가 촬영한 이미지에는 접근할 수 있다. 따라서 이미지에서 이러한 파라미터를 deduce(추론하는) 방법을 찾을 수 있는가? extrinsic과 intrinsic 카메라 파라미터를 추정하는 문제를 camera calibration이라 한다.
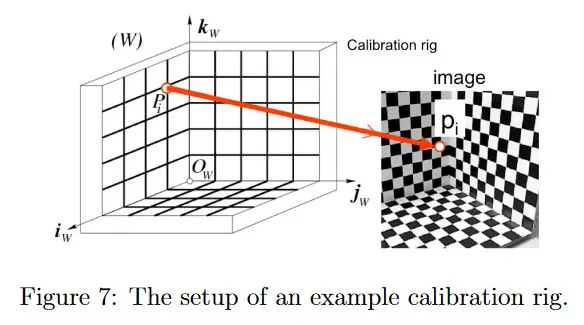
구체적으로 방정식 10에서 intrinsic 카메라 행렬 와 extrinsic 파라미터 을 구하는 방식으로 이를 수행한다. 이 문제를 그림 7과 같은 calibration rig(도구)의 맥락에서 설명할 수 있다. rig은 일반적으로 알려진 차원을 갖는 단순한 패턴(예: 체커보드)로 구성된다. 또한 rig은 원점 와 축 으로 world reference frame을 정의한다. rig의 알려진 패턴으로부터 world reference frame에서 알려진 점 을 얻을 수 있다. 카메라로 촬영한 이미지에서 이러한 점들을 찾으면 이미지 상의 대응점 을 얻는다.
개 대응점에서 선형 방정식을 설정한다. 각 대응점 와 행이 인 카메라 행렬 에 대해 다음과 같이 한다.
위의 방정식에서 볼 수 있듯이 각 대응점은 에 포함된 미지수 파라미터를 구하기 위한 2가지 방정식, 즉 2가지 제약 조건을 제공한다. 앞서 카메라 행렬에는 11개 미지수 파라미터가 있다고 했다. 이는 이것을 해결하기 위해 최소 6개 대응점이 필요하다는 의미이다. 그러나 현실에서 측정은 종종 noisy 하기 때문에 더 많은 대응점을 사용한다. 이것을 명시적으로 보기 위해 과 를 와 연관시키는 한 쌍의 방정식을 유도할 수 있다.
이 대응점들의 개가 주어지면 전체 선형 방정식은 다음이 된다.
이것은 행렬-벡터 곱 형식으로 다음처럼 형식화 될 수 있다.
일 때 우리의 homogeneous 선형 시스템은 over-determined이다. 이런 시스템에서 은 항상 자명한 해가 된다. 게다가 다른 non-zero 해 이 존재하면 에 대해 도 해가 된다. 따라서 해를 구체화하기 위해 위해 다음의 최소화 문제를 풀어야 한다.
이 최소화 문제를 해결하기 위해 간단히 singular value decomposition(SVD)를 사용한다. 이라 하면 위의 최소화 문제에 대한 해는 을 의 마지막 열로 설정하는 것이다. 이 해에 대한 유도는 이 수업의 범위를 벗어나므로, 상세 내용은 Hartley & Zisserman의 592-593 페이지 섹션 5.3를 참조하라.
벡터 을 행렬 으로 재형식화한 후, 이제 extrinsic과 intrinsic 파라미터를 명시적으로 해결하고자 한다. SVD로 구한 이 최대 규모로 알려져 있다는 것을 알고 있다. 즉 실제 카메라 행렬의 값이 의 스칼라 곱임을 의미한다.
여기서 과 은 의 3개 행이다. scaling 파라미터로 나누어 다음을 얻는다.
intrinsic에 대해 풀어서 다음을 얻는다.
extrinsic는 다음과 같다.
우리는 유도를 클래스 연습 문제로 남긴다. 또는 Forsyth & Ponce 교재의 섹션 1.3.1을 참조하라.
calibration 절차를 마친 후에 degenerate 사례를 주의해야 한다. 개의 대응점의 집합이 모두 이 작업에 해당하지 않음에 유의하라. 예컨대 점 가 동일 평면 상에 놓이면 시스템을 해결할 수 없다. 이러한 해결 불가능한 점들의 설정을 degenerate configuration이라 한다. 더 일반적으로 degenerate configuration은 점들이 2개의 quadric surface의 교차 커브 상에 놓인다. 이것이 수업의 범위를 벗어나지만 Forsyth & Ponce 교재의 섹션 1.3에서 더 많은 내용을 볼 수 있다.
6 Handling Distortion in Camera Calibration
지금까지 어떠한 distortion도 없는 이상적인 렌즈를 사용하여 작업했다. 그러나 이전에 본 것처럼 현실 렌즈는 rectilinear projection(직교 투영)에서 deviate(벗어날) 수 있으며 이를 처리하기 위해 더 발전된 방법이 필요하다. 이 섹션에서 distortion을 다루는 간략한 소개를 제공한다.
종종 distortion은 radially symmetric인데, 이는 렌즈가 물리적으로 대칭이기 때문이다. 우리는 radial distortion을 isotropic transformation으로 모델링한다.
이것을 이전과 같이 방정식의 시스템으로 재작성하여 다음을 얻을 수 있다.
그러나 이 시스템은 더는 선형이 아니므로 비선형 최적화 기법을 사용해야 한다. 이것은 Forsyth & Ponce의 섹션 22.2에서 커버된다. 특정한 가정을 하면 calibration 문제의 비선형 최적화를 단순화할 수 있다. radial distortion에서 두 좌표계 와 사이의 비율이 영향을 받지 않는다는 것에 유의하라. 이 비율을 다음처럼 계산할 수 있다.
개 대응점이 가능하다고 가정하여 선형 방정식 시스템을 다음처럼 설정할 수 있다.
이전과 유사하게 이것을 SVD를 통해 해결할 수 있는 행렬-벡터 곱으로 제공할 수 있다.
과 가 추정되면 는 와 의 비선형 함수로 표현될 수 있다. 이것은 원래의 것보다 복잡성이 훨씬 단순한 비선형 최적화 문제를 해결하면 된다.
7 Appendix A: Rigid Transformations
기본적인 rigid 변환에는 rotation, translation, scaling이 있다. 이 부록에서는 이 수업에서 일반적인 유형인 3d 경우에 대해 커버한다.
3d 공간에서 점을 회전하는 것은 3개 좌표 축 주위로 회전시키는 것으로 표현할 수 있다. 좌표 축을 중심으로 회전할 때 일반적인 관례는 반시계 방향으로 회전하는 것이다. rotation을 직관적으로 생각하는 한 가지 방법은 각 자유도 대해 얼마나 회전하는지를 보는 것인데, 이를 Euler angles이라 한다. 그러나 이 방법은 특정 구성에서 회전에 대한 자유도를 잃게 되는 singularities 또는 gimbal lock을 발생시킨다.
이것을 방지하는 한 가지 방법은 rotation 행렬을 사용하는 것이다. 이것은 회전을 더 일반적인으로 표현하는 방식이다. rotation 행렬은 행렬식이 1인 정사각 직교 행렬이다. rotation 행렬 과 벡터 가 주어지면 결과 벡터 를 다음처럼 계산할 수 있다.
rotation 행렬이 행렬의 매우 일반적인 표현이기 때문에 각 축을 중심으로 하는 회전 를 다음처럼 표현할 수 있다.
행렬 곱의 관계 때문에 행렬곱 에 따라 회전은 처음에 z축을 따라 회전한 후, y축, 그 다음 x축으로 회전하여 얻을 수 있다.
translation 또는 displacement(변위)는 특정한 방향으로의 이동으로 설명된다. 3d 공간에서 우리는 3개의 값을 갖는 translation 벡터 를 정의한다. 3개 축의 각각에서 displacement로 로 표기 된다. 따라서 어떤 포인트 가 주어지면 에 의해 어떤 다른 포인트 로 평행이동 된다. 이것을 다음처럼 작성할 수 있다.
행렬 형식에서 translation은 homogeneous 좌표를 사용하여 작성될 수 있다. translation 행렬을 다음처럼 구성하면
그러면 는 와 동등함을 볼 수 있다.
우리 rotation 행렬 곱과 translation을 결합하기 원하면 homogeneous 좌표계를 사용하는 것이 이득이다. 벡터 를 로 회전한 다음 로 평행 이동한 결과 벡터 를 다음처럼 작성할 수 있다.
마지막으로 어떤 양 에 의해 특정한 방향으로 벡터를 scale 하기를 원하면 다음의 scaling matrix을 구성할 수 있다.
그러므로 벡터를 scale 한 다음 rotate 하고 translate 하면 최종 변환 행렬은 다음이 된다.
이러한 유형의 변환 모두가 affine transformation의 예임에 유의하라. 의 마지막 행이 이 아닐 때 projective transformation이 발생하는 것을 떠올려라.
8 Appendix B: Different Camera Models
이제 weak perspective model이라 알려진 간단한 모델을 설명한다. weak perspective 모델에서 점은 우선 orthogonal projection을 사용하여 reference 평면에 투영된 후 projective transformation을 사용하여 이미지 평면에 투영된다.
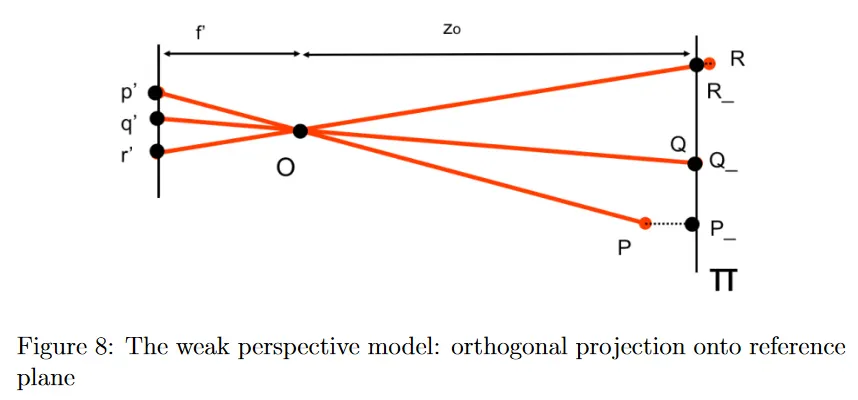
그림 8에서 보여지는대로 카메라의 중심에서 거리 만큼 떨어진 reference 평면 가 주어지면, 점 은 우선 orthogonal projection을 사용하여 평면 에 투영되어 점 을 생성한다. 이것은 카메라에서의 depth deviation가 평면까지의 거리에 비해 작을 때 합리적인 근사이다.
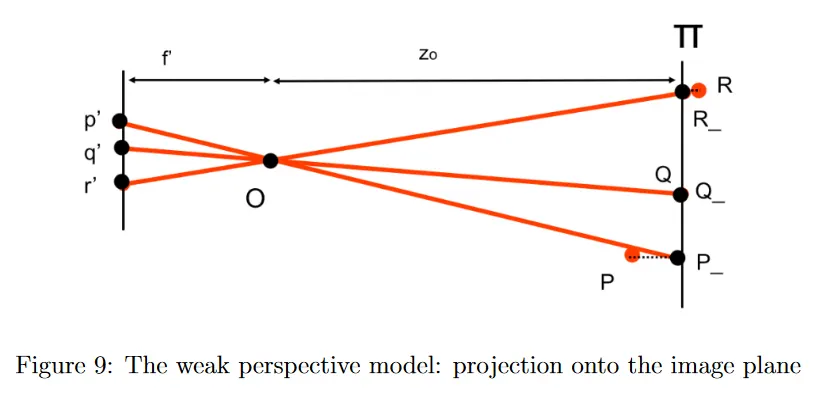
그림 9는 어떻게 점 가 regular projective transformation을 사용하여 이미지 평면에 투영되어 점 을 생성하는지를 보인다.
그러나 각 점의 depth를 로 근사했기 때문에 투영은 단순한 상수 배율로 축소되었음에 유의하라. 이 배율은 focal length 를 로 나눈 것과 동등하여 다음과 같이 된다.
이 모델은 projection 행렬로 단순화 된다.
weak perspective model에서는 의 마지막 행은 인 반면, normal camera model에서는 임을 볼 수 있다. 우리는 이 결과를 증명하지 않고 연습 문제로 남긴다. 3d 점을 이미지 평면에 매핑할 때 이 단순화가 명확히 드러난다.
따라서 이미지 평면 상의 점은 결국 depth와 관계없이 원래 3d 점의 배율이 된다. projective transformation의 비선형성은 사라지고, weak perspective transformation은 단순한 확대기가 된다.
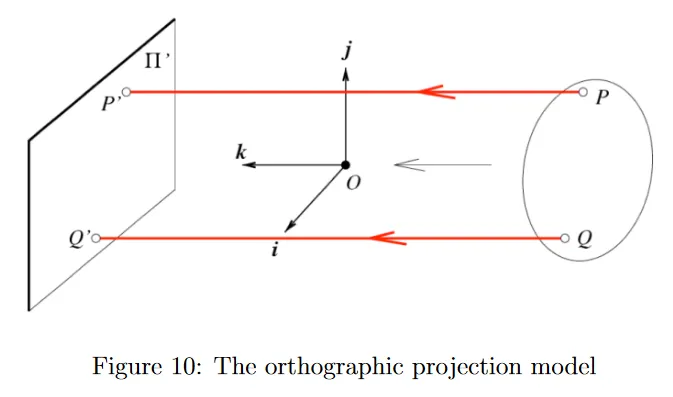
더 나아가 orthographic (or affine) projection model 모델로 단순화 할 수 있다. 이 경우에 optical 중심이 무한대에 위치한다. projection rays는 이제 retinal 평면에 perpendicular(수직)이 된다. 그 결과 이 모델은 depth를 모두 무시한다. 따라서
Orthographic projection 모델은 종종 건축과 산업 디자인에서 사용된다.
전체적으로 weak perspective model은 수학적 계산이 훨씬 단순해 지지만 다소 imprecise(부정확한)이다. 그러나 객체가 작고 카메라에서 distant(먼) 때 매우 근사 결과를 산출한다.