•
Linear model, softmax loss, gradient descent 까지 봤음
•
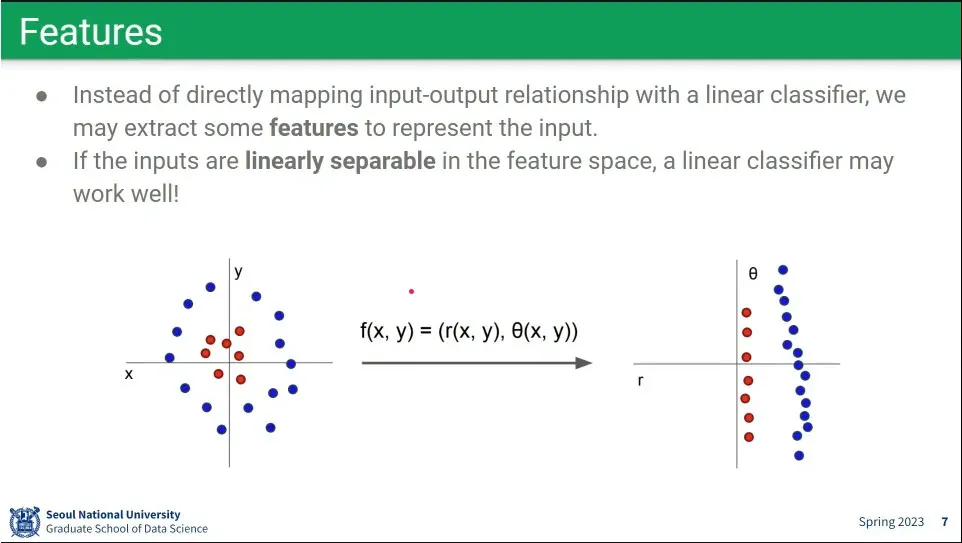
Linear 모델은 근본적으로 한계가 있음. 오른쪽 아래처럼 non-linear 한 경우에는 처리가 안
•
Linear로 해결하기 위해 애초에 feature를 linear하게 변형한 후에 처리하는 방법을 시도 해 봄.
◦
그러나 이런 경우는 많지 않음.
◦
많은 경우 차원을 높이면 linear로 해결 되는 경우가 많아서 그렇게 하는 경우도 있음.
•
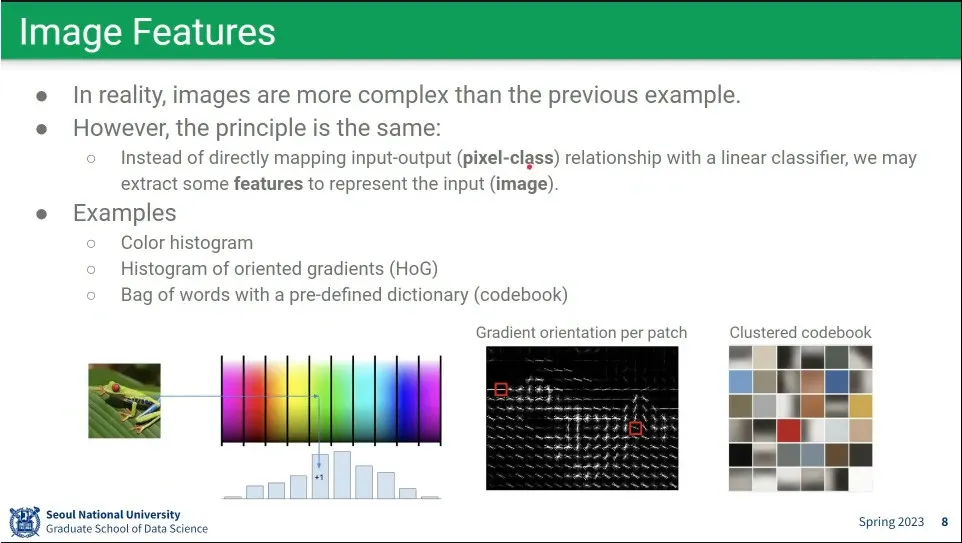
이미지에서 feature를 뽑기 위한 여러 방법
•
feature 기반을 발전 시켜서 이미지에서 feature를 뽑은 후에 그 feature를 label에 대응시킴.
◦
이게 pre-extracted feature이고 deep learning 이전에 쓰던 방
•
deep learning 시대로 오면서 아예 feature를 뽑는 것 자체도 학습 시킴. 이게 바로 end-to-end 방식
•
하지만 이게 항상 최선은 아님.
◦
엄청난 데이터와 계산량이 필요하기 때문에 다소 무식한 방법임.
◦
이미 알려진 domain knowledge 가 있다면 그것을 기계한테 다시 배우도록 학습 시킬 필요가 없음.
•
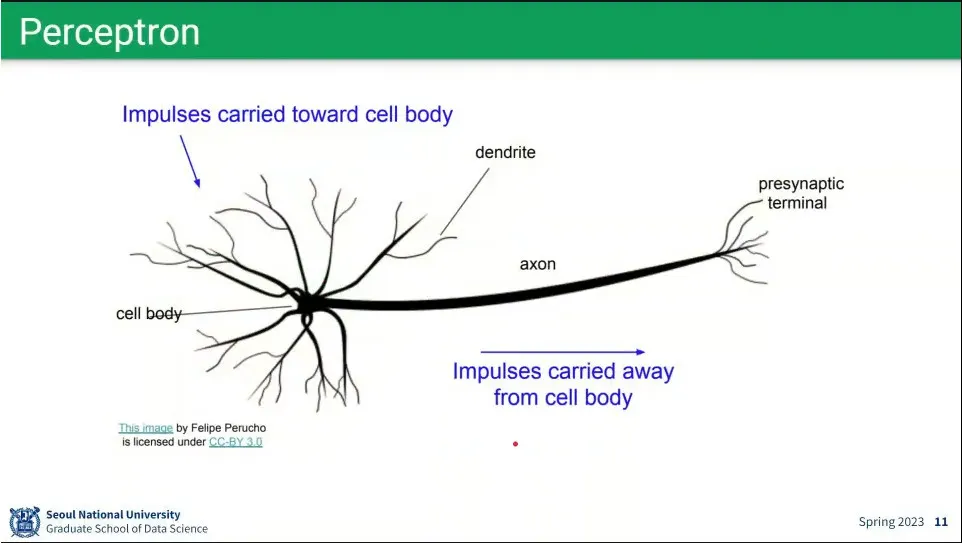
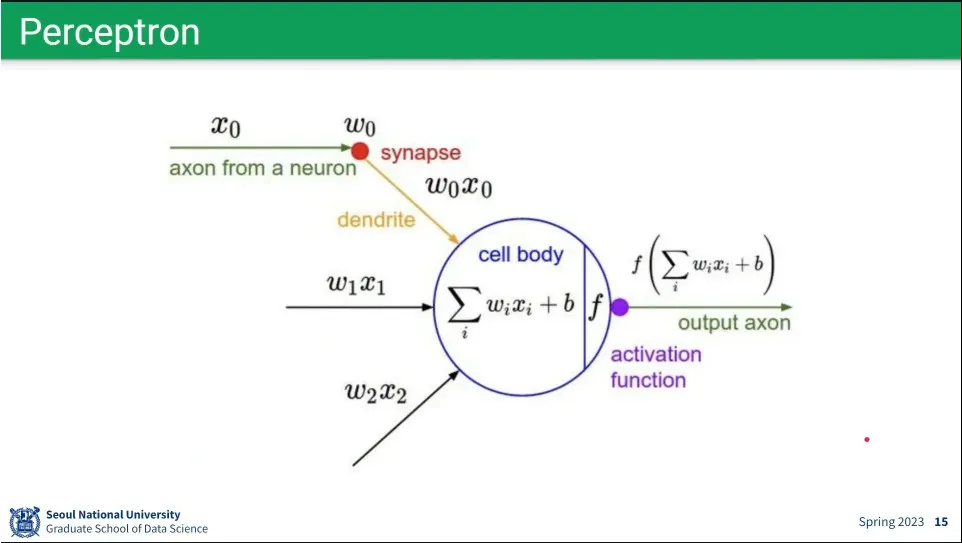
neural network는 인간의 뉴런을 모사한 방법
•
뉴런을 모사해서 perceptron을 만듦. 뉴럴 네트워크는 perceptron을 모아 놓은 것.
•
perceptron을 이용하면 논리 연산이 가능함.
◦
이전 노드가 켜지고 꺼지고를 이용해서 and, or 연산을 할 수 있음.
◦
not, and, or만 있으면 모든 연산이 가능하다. xor도 not, and, or로 만들 수 있음.
•
그런데 perceptron을 이용해서 XOR 연산이 안 됐음. 이것 때문에 1차 AI 겨울이 옴
•
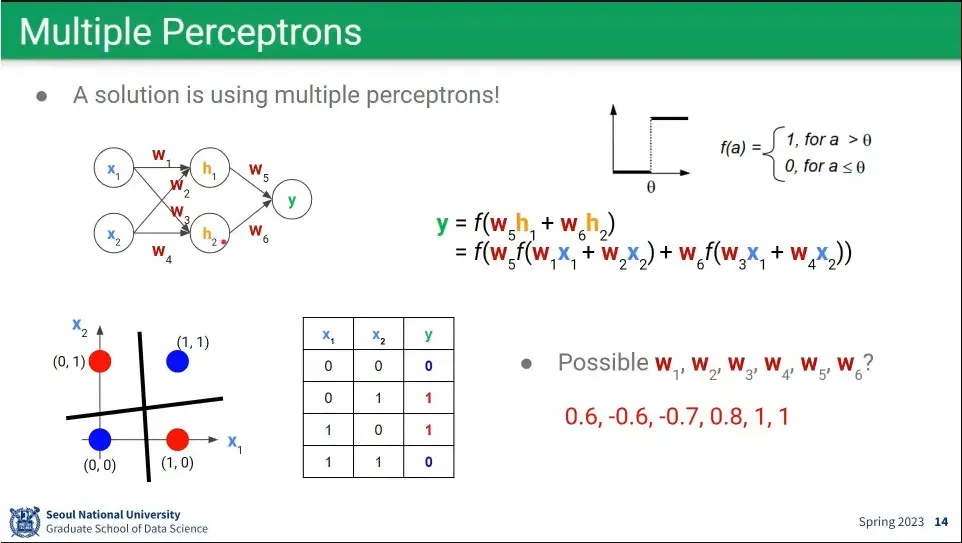
이걸 해결한 사람이 제프리 힌튼. perceptron을 2층으로 쌓으면 XOR 연산도 가능함을 증명 함.
◦
2층을 쌓으면 어떤 조건 하에 모든 식이 가능하고, 3층을 쌓으면 아예 조건도 필요 없이 모든 식이 가능하다는 것을 제프리 힌튼이 수학적으로 증명 함.
•
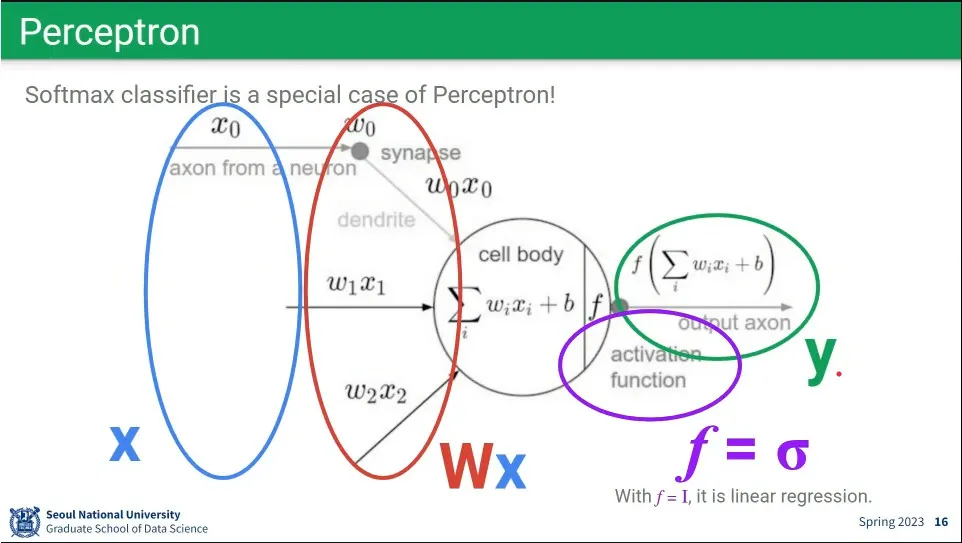
퍼셉트론 구조는 softmax classifier와 동일하다.
•
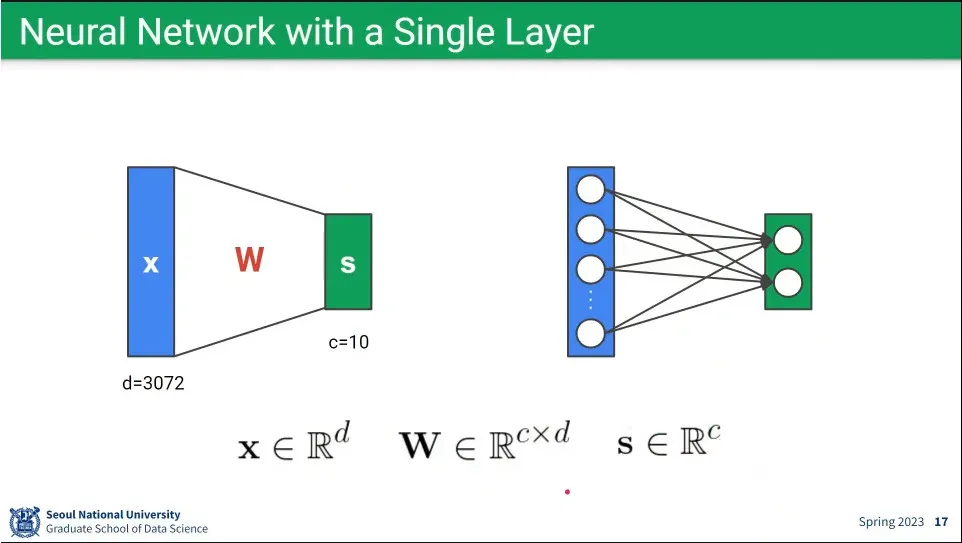
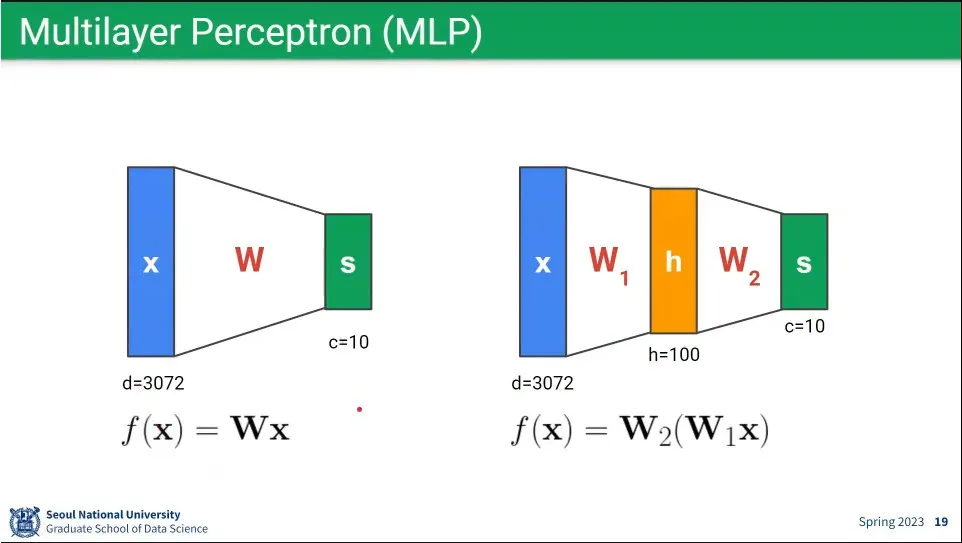
single layer의 뉴럴 네트워크는 위와 같이 표현 가능
•
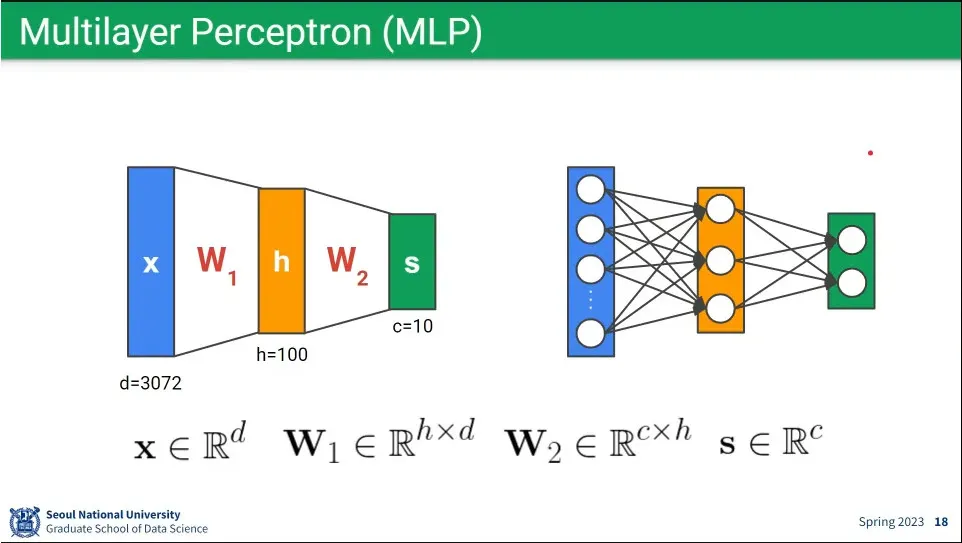
multi layer의 뉴럴 네트워크는 위와 같이 표현 가능
•
행렬식으로만 보면 single layer나 multi layer는 동일하게 볼 수 있음.
•
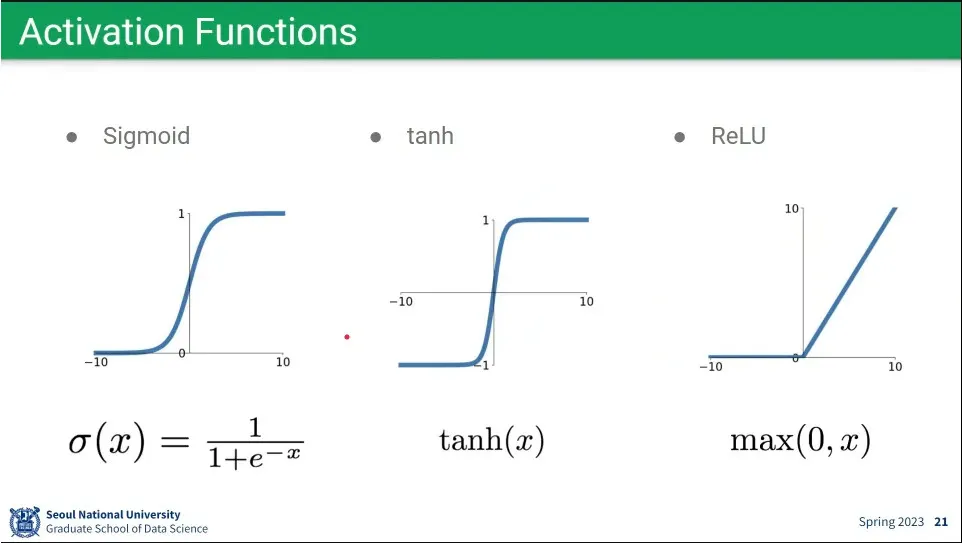
single layer와 multi layer의 차이는 activation function의 차이
•
많이 쓰이는 activation functions
•
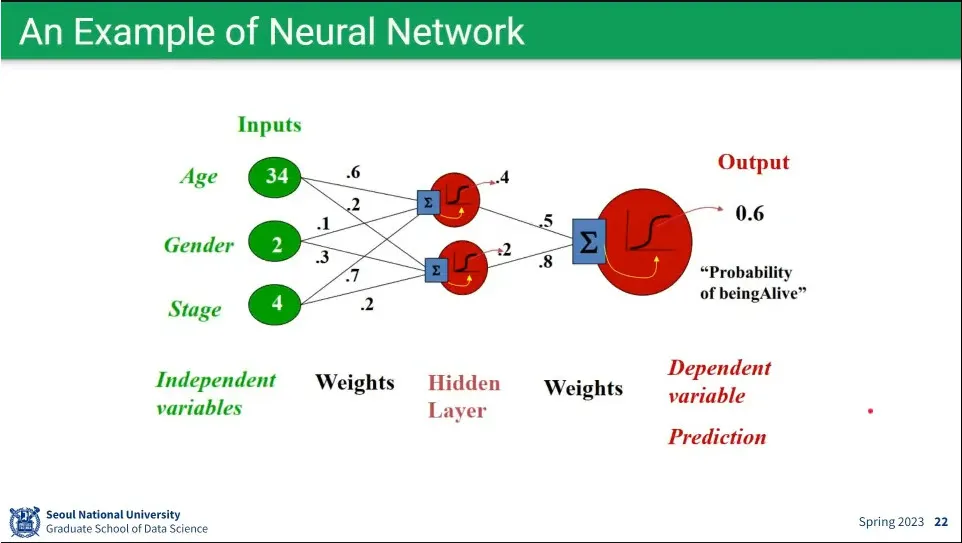
뉴럴 넷 예시
•
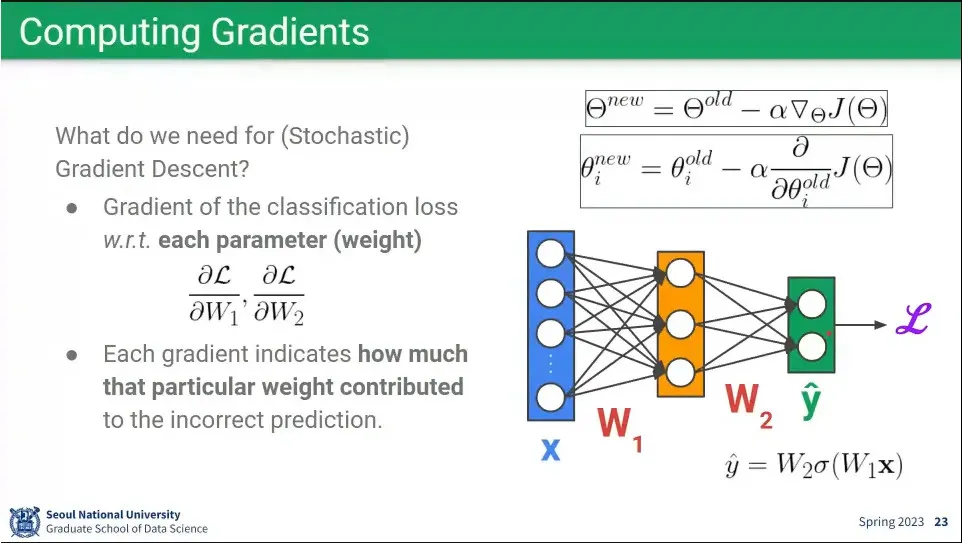
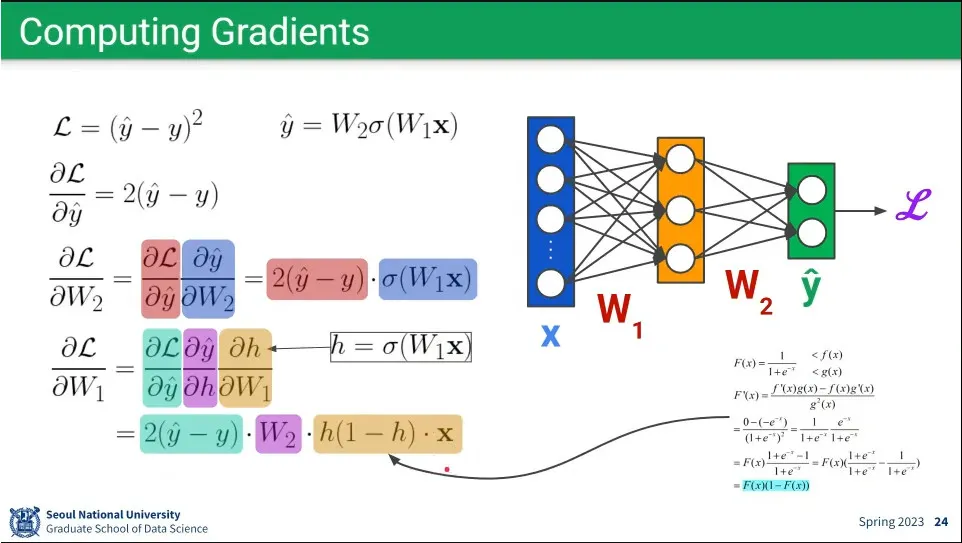
W는 gradient descent로 구할 수 있다.
•
Loss를 W2, W1으로 편미분하는 예시
•
코드 예시
•
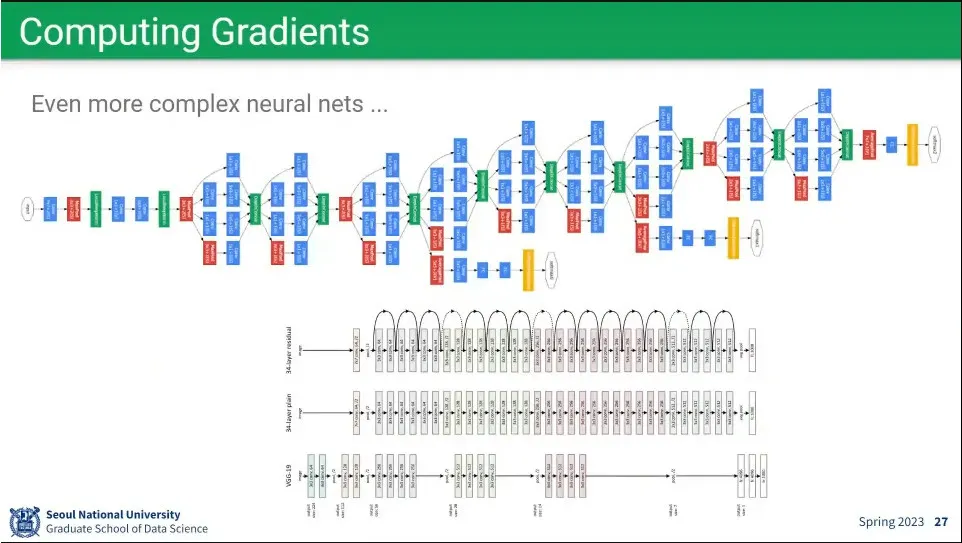
문제는 이걸 손으로 풀고 있을 수 없음.
•
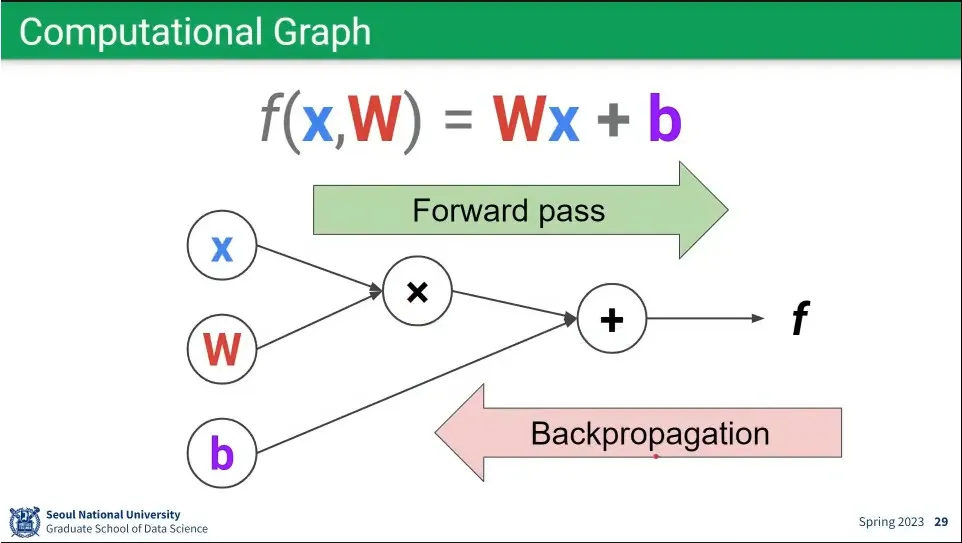
연산을 그래프로 표현.
◦
앞으로 가는 계산이 forward pass이고, 거꾸로 오는 것이 backpropagation
•
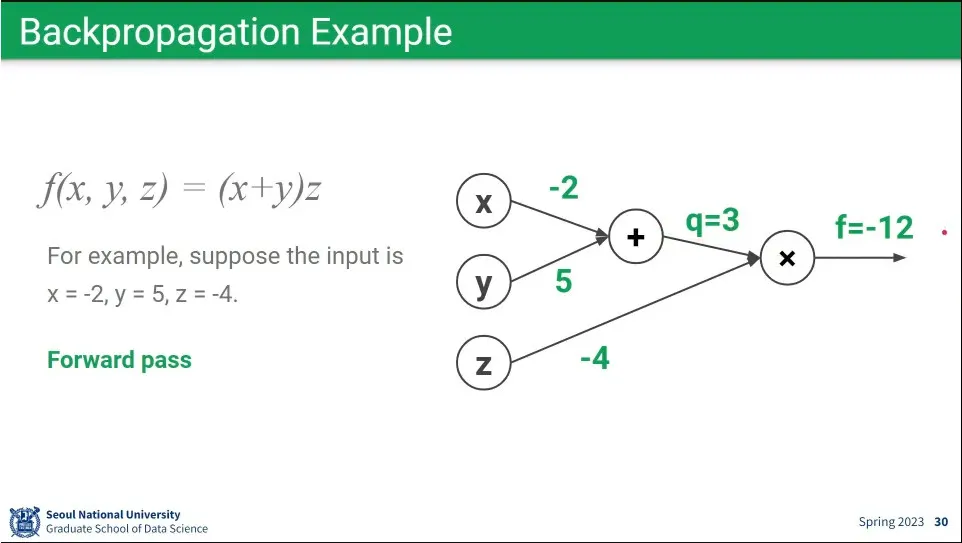
forward 예시
•
backpropagation 예시
•
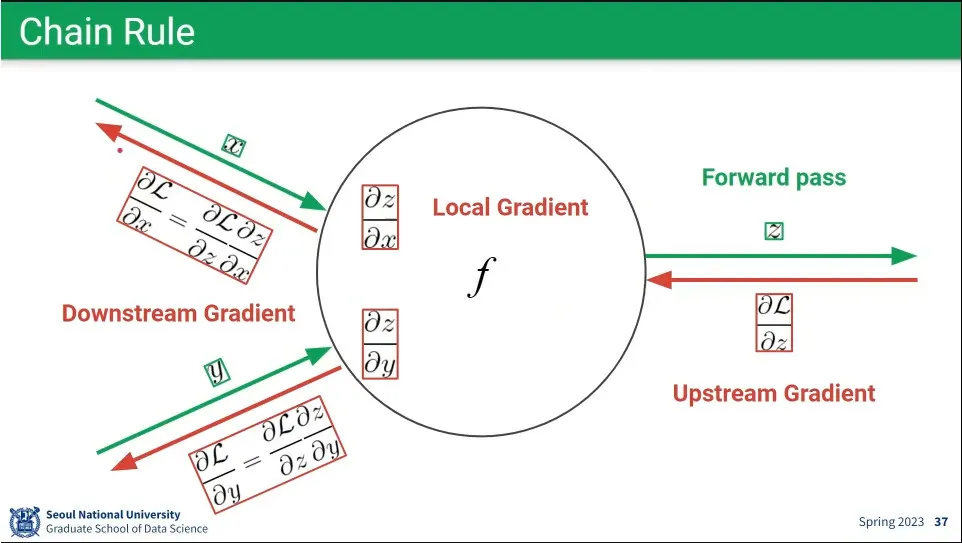
backpropagation은 upstream gradient에 local gradient를 곱하면 downstream gradient가 된다. 이게 chain rule.
◦
이런 식으로 예측 결과에서부터 입력 layer까지 거꾸로 타고 가는 것
•
logistic regression에 대한 forward pass, backpropagation 예
•
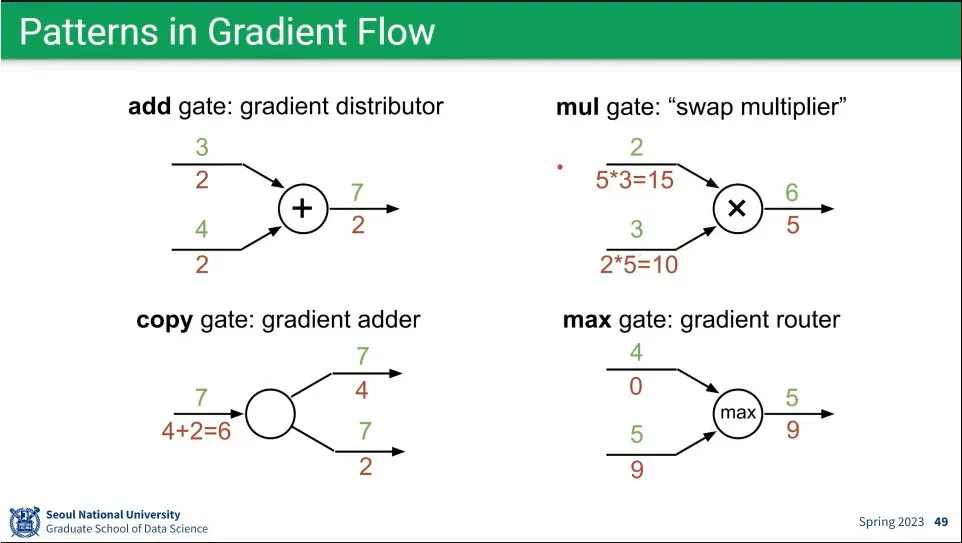
gradient 계산의 패턴
◦
이런 패턴을 이용하면 복잡한 계산을 하지 않고 최적화를 할 수 있음.
◦
물론 현재는 tensorflow나 pytorch가 그것을 해줌.
•
앞선 예제의 코드 예시
•
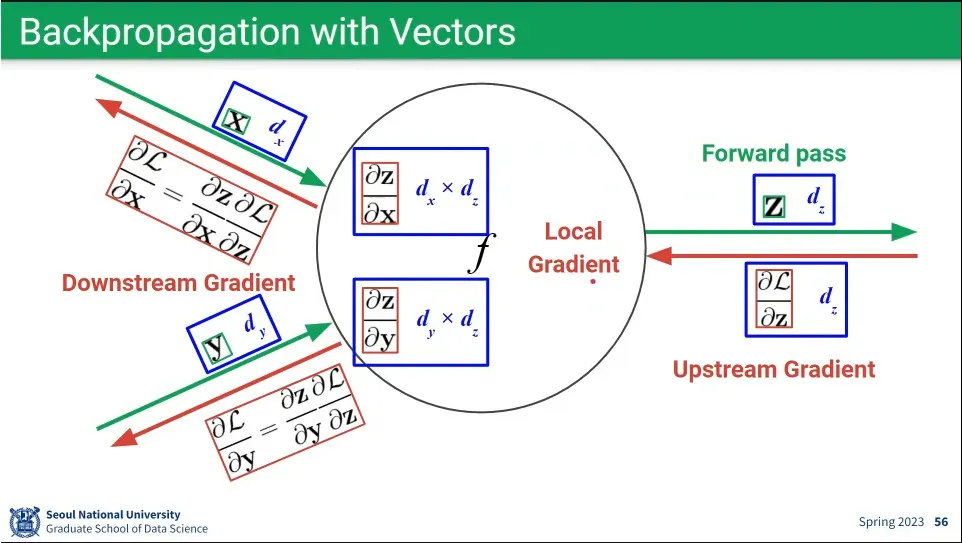
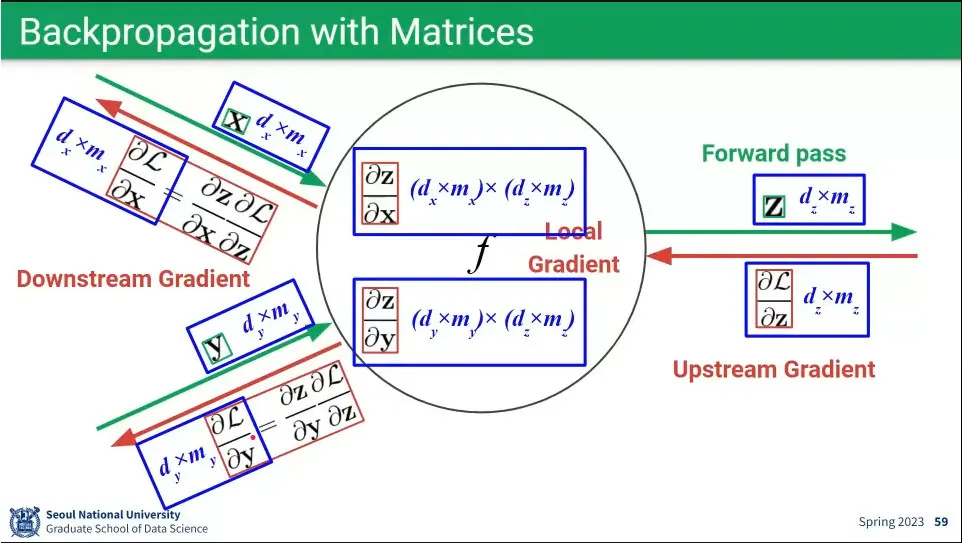
앞선 예시는 scalar를 이용한 것이었는데, 대부분의 경우 vector나 matrix를 이용하게 됨. 하지만 계산을 여러 번 하는 것일 뿐 그 방법은 동일하다.
•
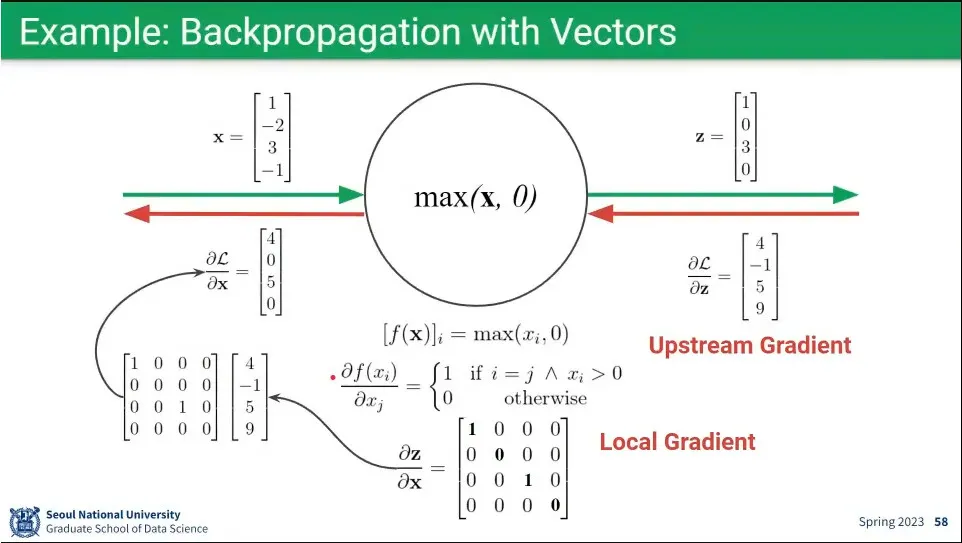
예시
•
행렬도 계산량이 많을 뿐 결국 동일하다.