•
Supervised
◦
정답이 있음
◦
데이터를 정답으로 매핑 해주는것
◦
그래서 functional approximation이라고 함
•
Unsupervised
◦
정답이 없음
◦
데이터 자체가 가진 숨겨진 구조를 학습함
•
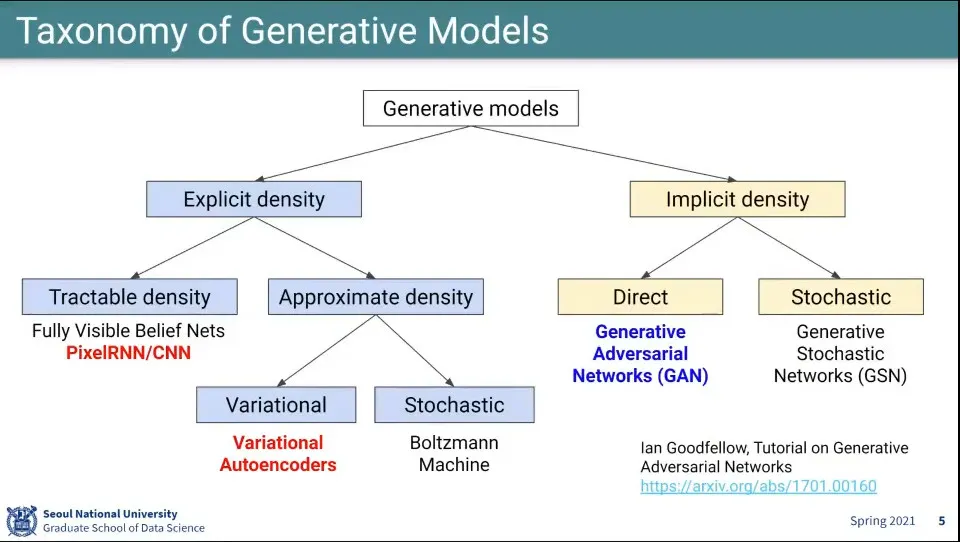
Generative Modeling이라는 것은 데이터로부터 어떤 분포를 추정하고, 그게 맞는지 검증하기 위해 그 모델로 새로운 데이터를 생성해 냄
◦
이 모델을 라고 한다.
•
Explicit Density Estimation은 를 분명하게 정의는 방식이고
•
Implicit Density Estimation은 를 분명하게 정의하지 않고 사용하는 방식
•
생성 모델이 사용되는 곳
•
supervised learning에 사용할 feature를 생성하기 위해서도 사용한다.
•
고차원적인 통찰을 얻고자 할 때도 쓴다 (물리학이나 생물학, 의학 등에서 쓰임)
•
생성 모델의 Explicit, Implicit 방식 구분
•
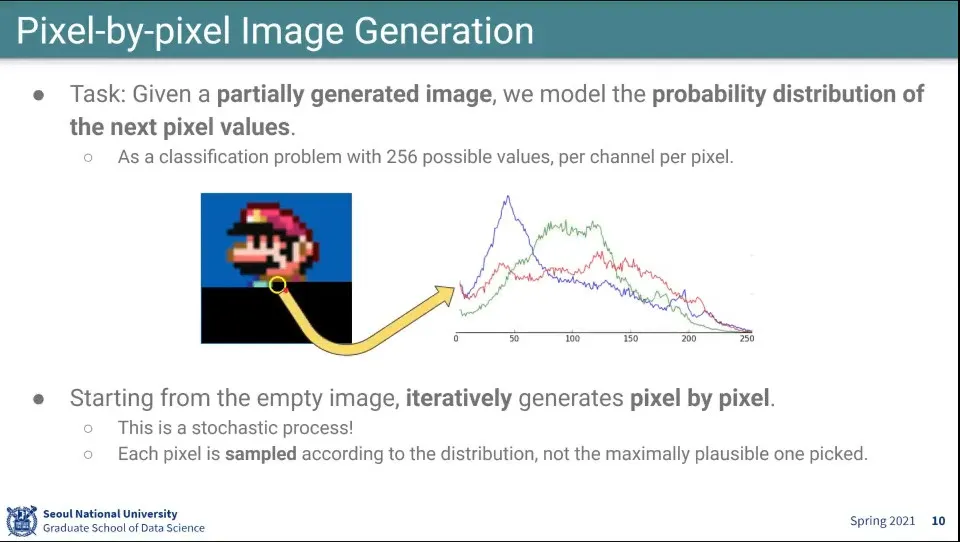
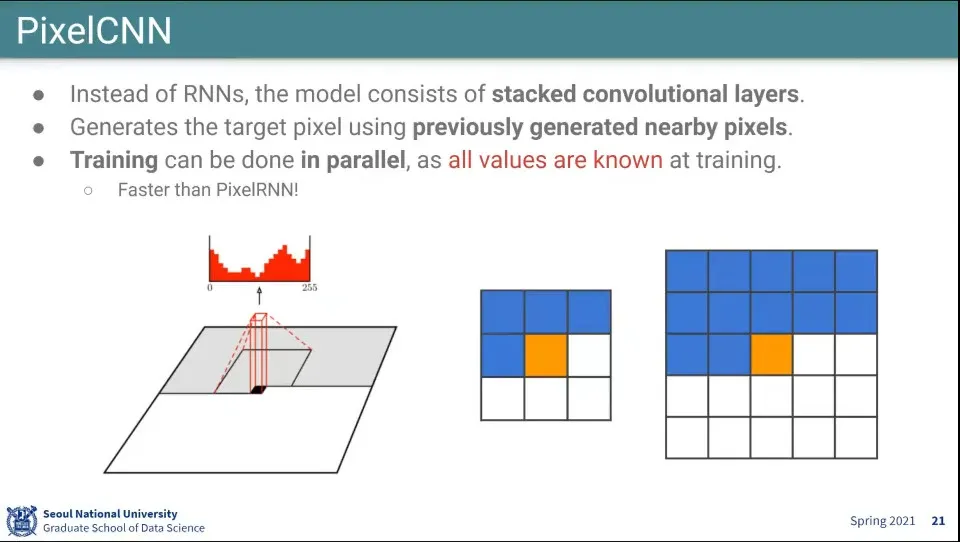
Pixel 단위 이미지 생성
◦
Pixel에 어떤 순서를 정의함
•
부분적으로 만들어진 이미지에 대해 나머지 부분을 채움
◦
이때 픽셀 단위로 RGB 분포를 예측함
•
근데 이걸 그대로 쓰면 항상 똑같은 그림만 나오기 때문에 위 분포에 대해 샘플링해서 함
•
chain rule을 이용해서 이미지의 likelihood를 1차원 분포들의 곱으로 분해함
•
크기의 이미지라면 총 의 픽셀이 주어지고
◦
번째 픽셀을 예측하기 위해 부터 번째까지의 픽셀 값을 조건으로 넣어서 번째 픽셀을 예측함
▪
◦
이때 하나의 픽셀은 RGB 값을 가지므로 하나의 픽셀에 대해서도 이전 픽셀들 값, R, G, B를 순서대로 조건으로 넣어서 예측한다.
▪
▪
(위 슬라이드 수식에는 뒷부분이 잘못 표기되어 있음. R을 예측할 때 이전 픽셀값들이 조건으로 들어가고, G를 예측할 때 이전 픽셀들 값과 예측한 R값이 들어가고, B를 예측할 때 이전 픽셀들값과 예측한 R, G가 들어간다)
•
당연히 이렇게 하면 매우 느림
•
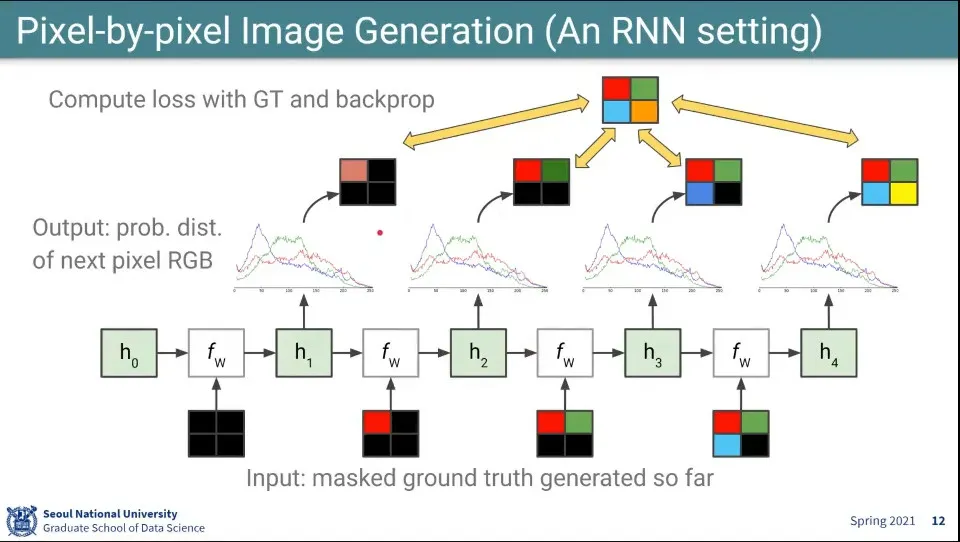
여기서 픽셀을 생성하는 것은 RNN과 비슷하다.
1.
일단 hidden state를 설정하고
2.
빈 input을 넣어서 계산한 후 hidden state를 업데이트 함
3.
업데이트된 hidden state에서 output을 출력하고
4.
그것을 원래 만들고자 했던 이미지와 비교하고 backpropagation을 수행함
5.
다음 state에서는 이전 state의 output을 쓰지 않고, 원래 만들고자 했던 이미지(정답)을 input으로 넣어서 2-4 반복
•
위 과정을 좀 더 효율적으로 하려고 LSTM을 사용해 봄
◦
일반적으로 RNN을 한다고 하면 LSTM을 한다고 보면 된다.
•
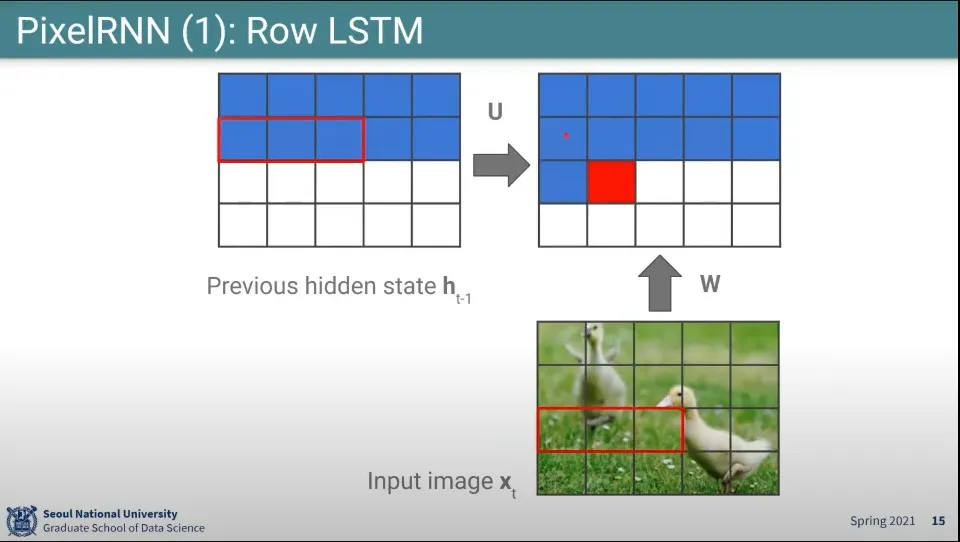
이때 그냥 곱하지는 않고 conv 처럼 곱함. 주위 픽셀을 봐야 하기 때문
•
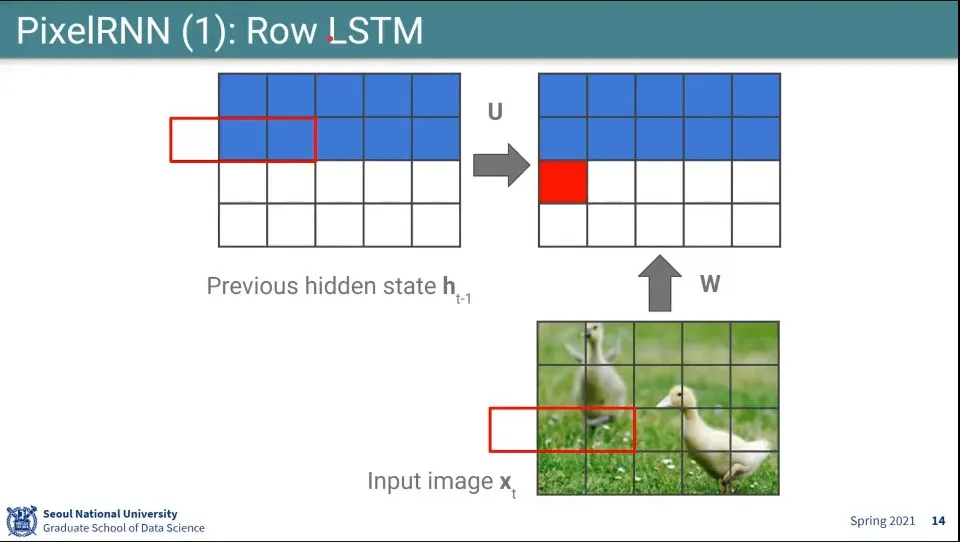
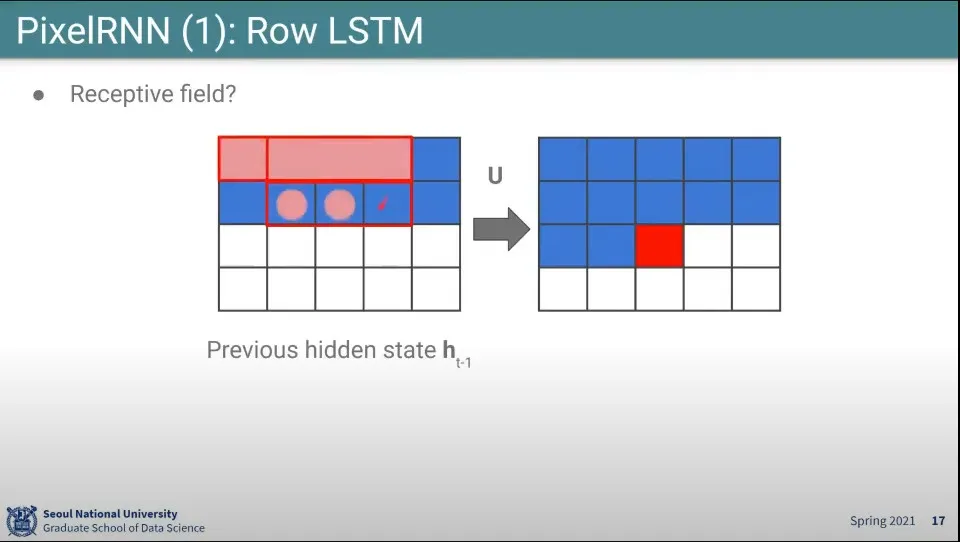
Row LSTM이라서 줄 단위로 수행함
◦
2번째 줄까지 된 상태에서 위와 같이 전단계(이전 row) state 3개와 input image의 현재 row에 대해 3개 픽셀씩 곱해서 사용 함. 한칸씩 움직이며 채운다.
◦
이래서 conv 처럼 계산된다고 한 것
•
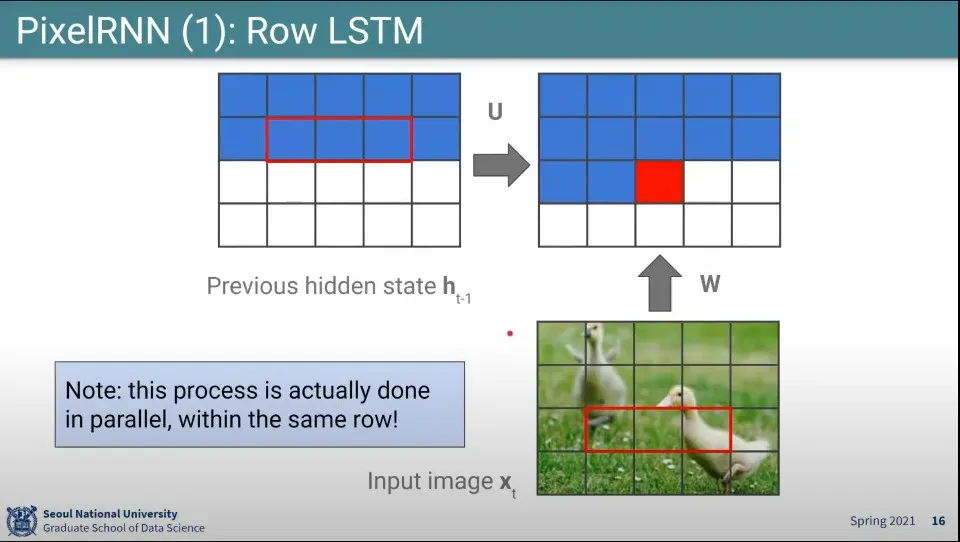
이거는 전단계가 만들어져 있기 때문에 해당 row에 대해서는 parallel로 수행이 가능함.
◦
줄 단위로는 sequencial 하지만 칸 단위로는 parallel로 수행 가능
•
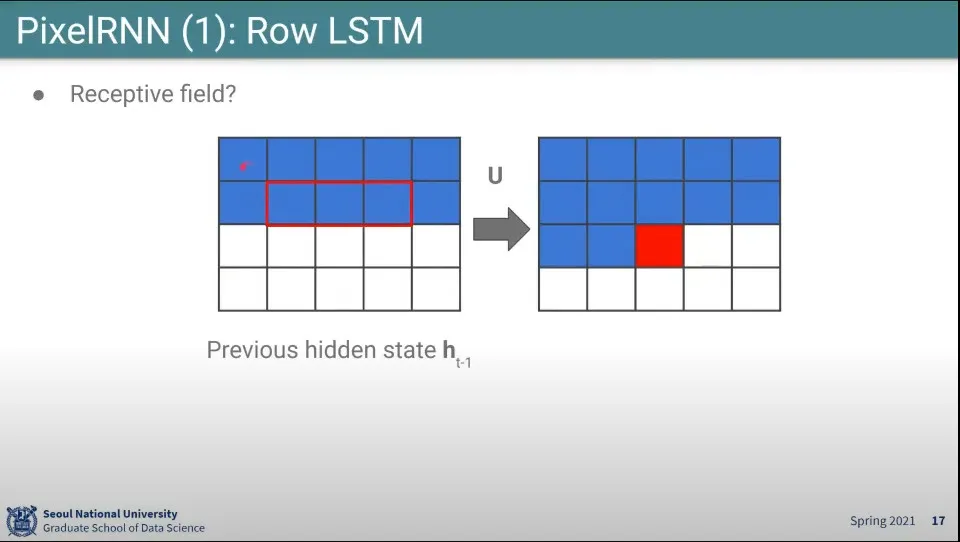
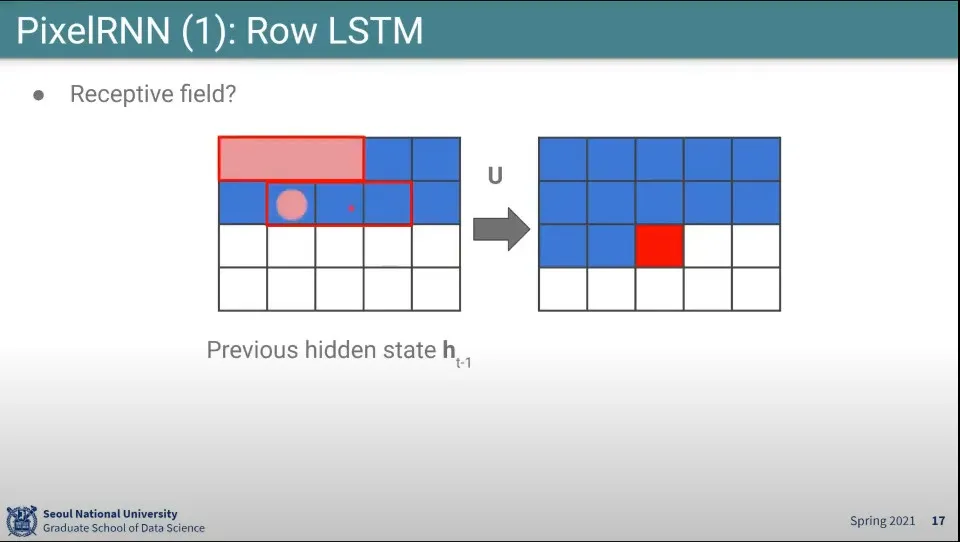
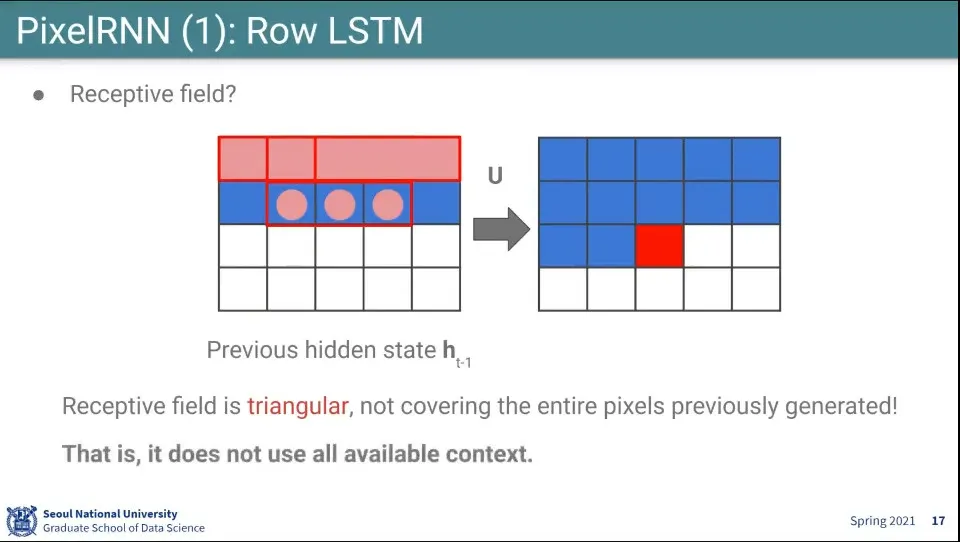
하나의 픽셀을 생성할 때 영향을 주는게 바로 위의 3개 픽셀이고, 그 위의 3개 픽셀은 다시 그 위의 픽셀 3개씩을 보고 만든다.
•
이렇게 되면 하나의 픽셀을 만드는데 영향을 주는 픽셀이 위로 삼각형을 그리게 됨.
◦
때문에 사각지대가 생김. 전체 context를 이용하지 못한다.
•
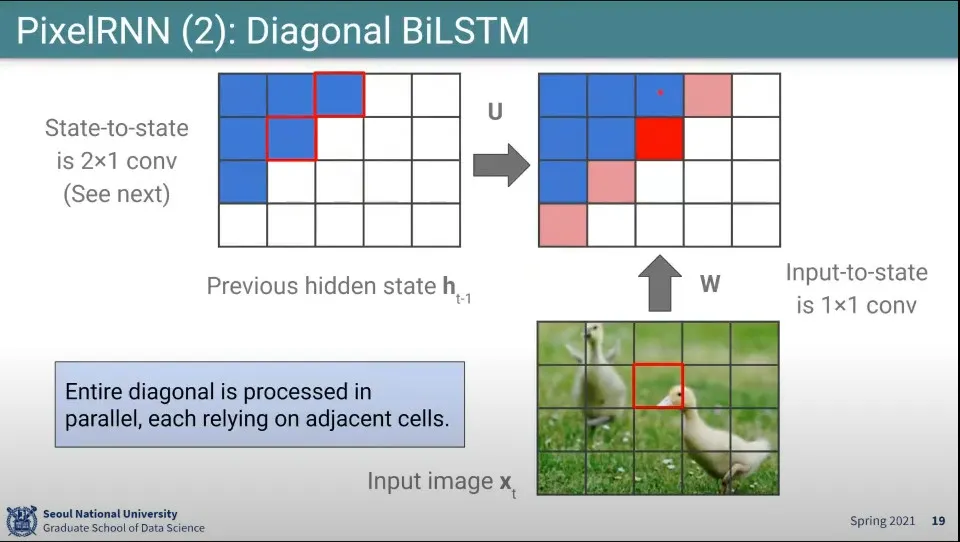
삼각형 문제를 해결하기 위해 개선된 것이 Diagonal BiLSTM
•
식은 동일하지만, 그리는 순서를 대각선으로 하고, 그릴 때, 왼쪽과 위쪽 픽셀을 참조해서 그림
◦
이러면 결과적으로 자신의 왼쪽, 자신의 위쪽에 속한 모든 픽셀들에 의해 영향을 받을 수 있음
•
이것도 마찬가지로 parallel하게 수행 됨
•
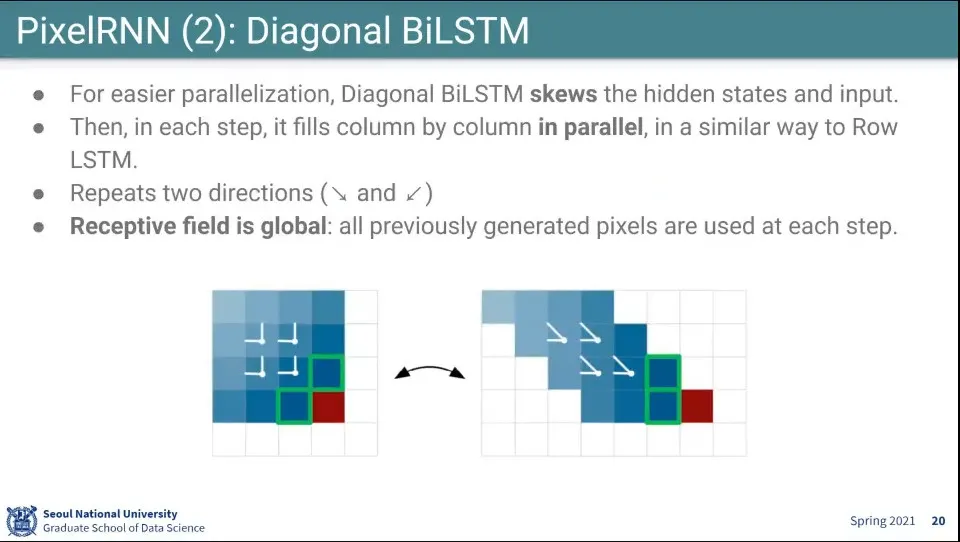
대각선으로 참조하는게 계산하기 복잡하므로, input image를 오른쪽과 같이 계단식으로 shift해서 학습을 돌림
◦
이렇게 하면 1x2 크기로 conv 계산을 할 수 있음
•
추가로 오른쪽 아래로 내려가는 방향과 왼쪽 아래로 내려가는 방향을 모두 이용해서 2번 그림
◦
이러면 자신의 row이상의 모든 pixel에 영향을 받을 수 있음
•
앞의 것과 달리 CNN을 이용해서 생성함
◦
다만 이렇게 하면 아직 안 만들어진 pixel을 쓸 수 없기 때문에 filter에 오른쪽처럼 mask를 씌워서 학습 함
•
학습할 때는 이미지가 이미 있기 때문에 모든 픽셀에 대해 parallel하게 할 수 있음
◦
그러나 inference 할 때는 parallel로 할 수 없음
•
Pixel CNN의 Mask는 2개가 있는데
◦
Mask A는 이전 Pixel과 RGB까지 보고 생성함
▪
만일 현재 G를 생성하려면 이전 Pixel과 현재 Pixel의 R까지 보고 만듦
◦
Mask B는 이전 Pixel과 현재 RGB까지 보고 생성함
▪
만일 현재 G를 생성하려면 이전 Pixel과 현재 Pixel의 R과 G까지 보고 만듦
•
이것을 이용해서 처음 학습할 때는 Mask A로 학습하고, 그 뒤에 Mask B로 한 번 더 학습함
•
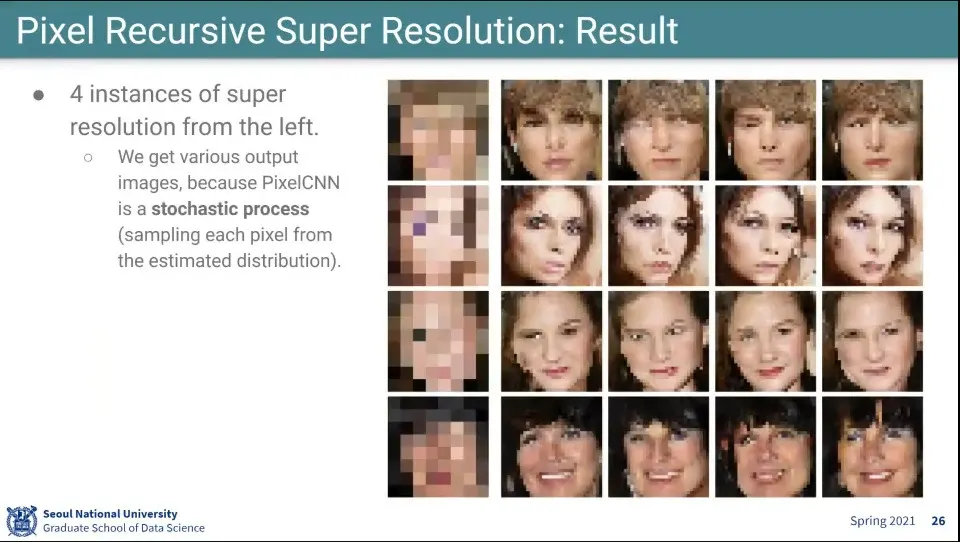
위 방법을 이용해서 Super Resolution에 사용함
◦
그럴싸한 것을 만들어주기는 하지만 완벽하지는 않음 —만들어낸 사람이 원래 사람과 다른 사람이 나옴. 그리고 만들 때마다 다른 사람이 나옴
•
는 낮은 해상도의 input 이미지를 말함. 낮은 해상도의 픽셀은 L 픽셀이라고 함
•
는 높은 해상도의 예측 결과를 말함. 높은 해상도의 픽셀은 M 픽셀이라고 함. —보통 를 쓰는데 이 논문에서는 를 씀
•
는 높은 해상도의 정답 이미지를 말함. 학습할 때 사용 됨
•
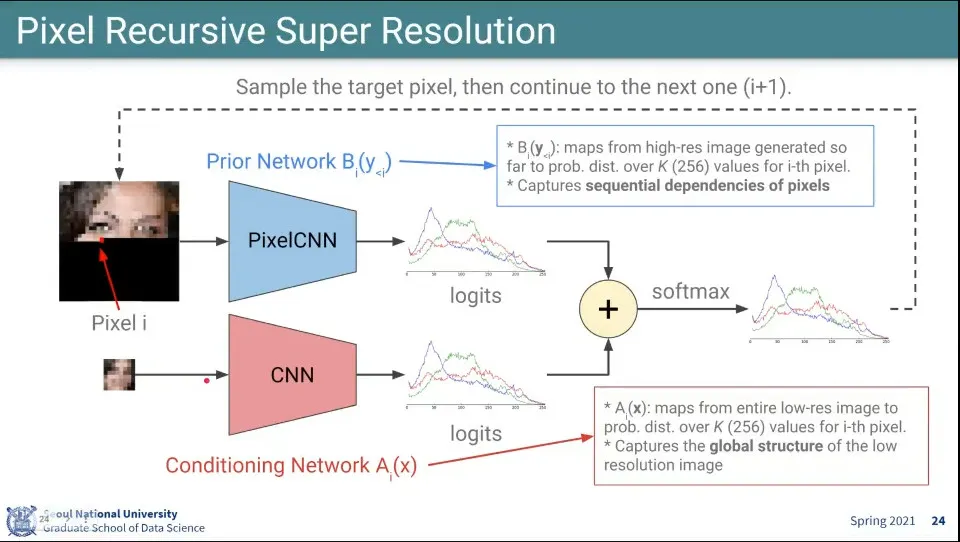
학습할 때는 2개의 Network를 사용함.
◦
PixelCNN을 통해 높은 해상도에서 새로운 pixel을 예측함. 이걸 Prior Network라고 함.
◦
낮은 해상도의 이미지에서 대해 CNN을 돌려서 픽셀 분포를 예측함. 이걸 Conditioning Network A라고 함.
▪
낮은 해상도의 이미지에 대해서는 filter를 씌우지 않고 전체 구조를 파악하는데 사용함
◦
위 2개의 결과를 합치고 softmax를 씌워서 최종적으로 pixel을 생성함
•
위의 2개 모델이 계산하는 수식
◦
위에는 예측이고, 아래는 loss 계산
•
stochastic 이기 때문에 같은 input에 대해 다른 결과물이 나옴
◦
확률 분포에 대해 sampling을 해서 수행
•
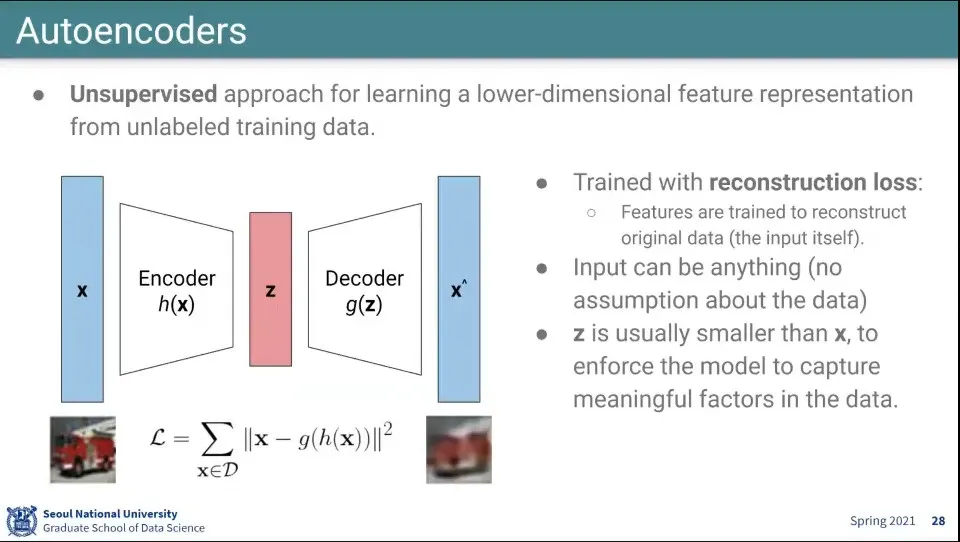
Autoencoder는 Unsupervised 학습
◦
데이터에 대해 낮은 차원의 대표성을 갖는 feature 학습
◦
loss 함수는 원래 input과 생성해낸 output과의 차이의 제곱을 최소화하는 방향으로 이루어지게 됨
•
Autoencoder에는 어떤 데이터도 들어올 수 있음
◦
데이터를 저차원 Z으로 만드는 encoder와
◦
Z를 다시 원래 차원으로 복원하는 decoder를 가짐
◦
원래 차원으로 복원 시키기 위해 필요한 가장 핵심적인 feature를 스스로 학습 개념
◦
때문에 Z는 X보다 작아야 하며 (상당히) Z를 bottle neck layer라고 함
•
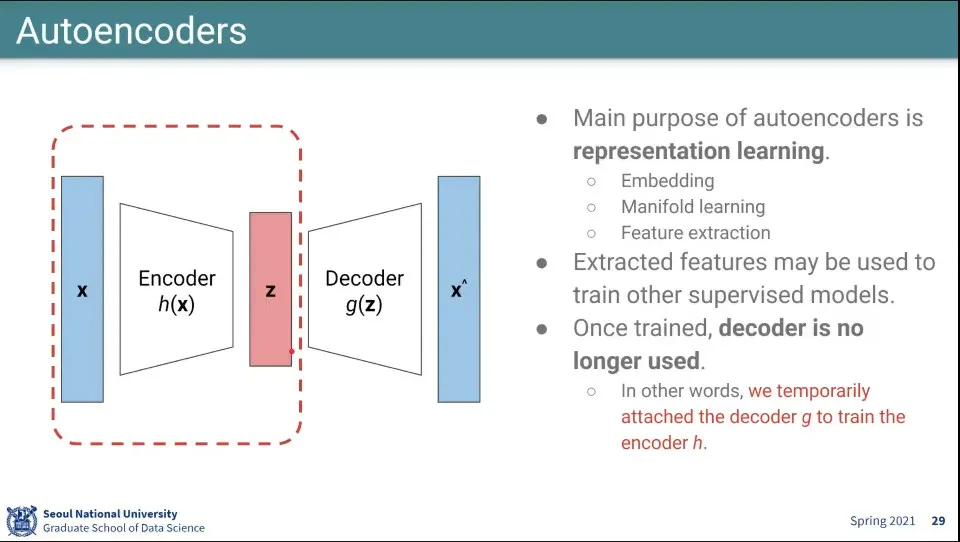
Autoencoder는 labeling 없이 학습할 수 있음
•
Autoencoder는 Embedding, Manifold learning, Feature extration을 위해 사용함
•
Decoder는 training에서 loss를 매기기 위해 하는 거고, 실제로 사용하는 부분은 encoder 부분만 사용함
•
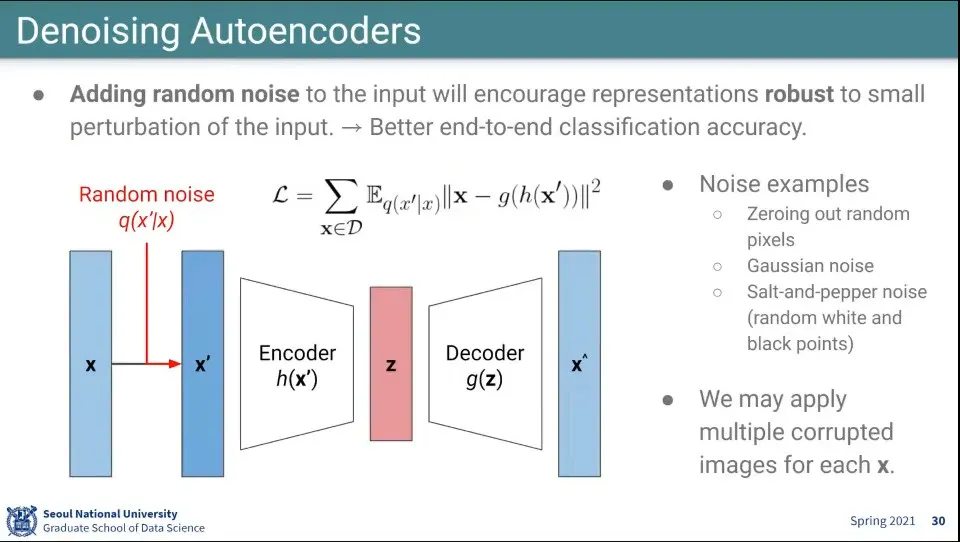
Autoencoder를 조금 더 잘하기 위해 random noise를 넣어서 하는게 Denoising Autoencoder
◦
랜덤하게 0으로 만들거나
◦
가우시안 노이즈를 주거나
◦
소금 후추 노이즈를 줄 수 있음 —일부 픽셀의 컬러를 바꾸는 등
•
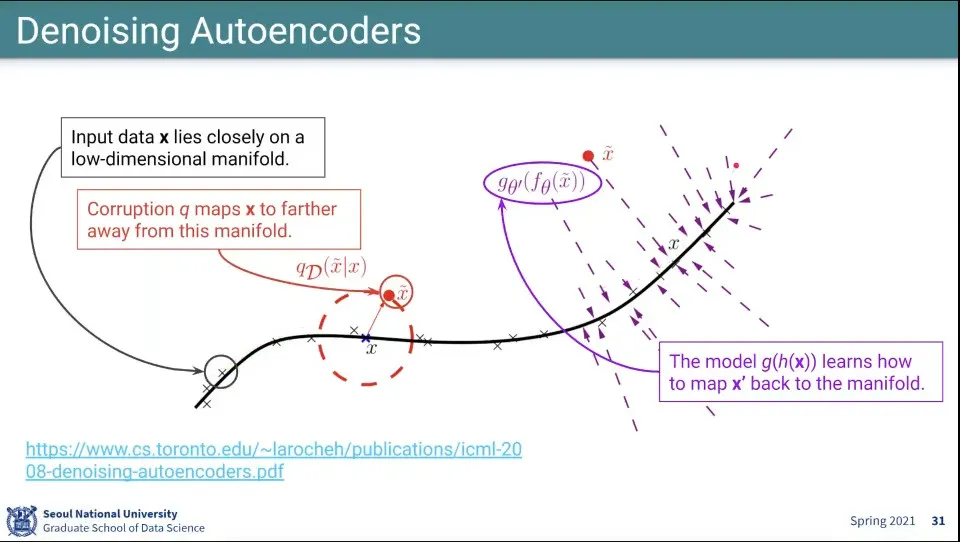
노이즈를 추가해서 원래 manifold에서 벗어나게 한 후에 그것을 다시 원래 manifold로 끌고 오게 하는 것
•
근데 Autoencoder는 실용적으로는 잘 쓰이지 않음. Encoder가 어느 정도 의미를 갖지만 결국 만들어 내는게 블러가 많이 들어가기 때문
•
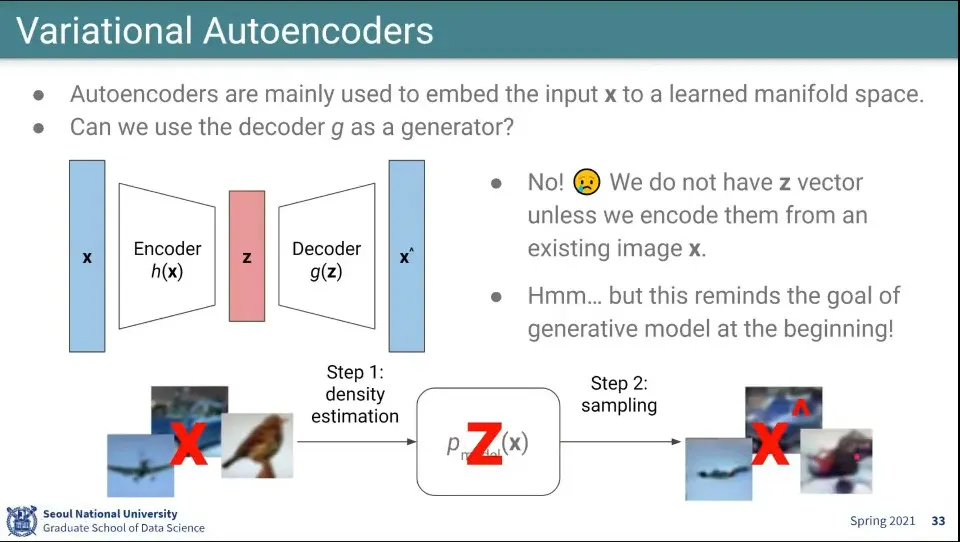
Autoencoder가 Encoder만 썼던 것과 반대로, 압축된 차원 Z로부터 Decoder를 통해 어떤 것을 생성하는 것에 대한 아이디어
◦
이것은 이미지에서 어떤 분포를 보고 학습한 후에 샘플링을 하는 것과 동일함
•
Autoencoder는 Embedding하는 모델이었던 반면 여기서는 반대로 생성 모델을 만든다.
◦
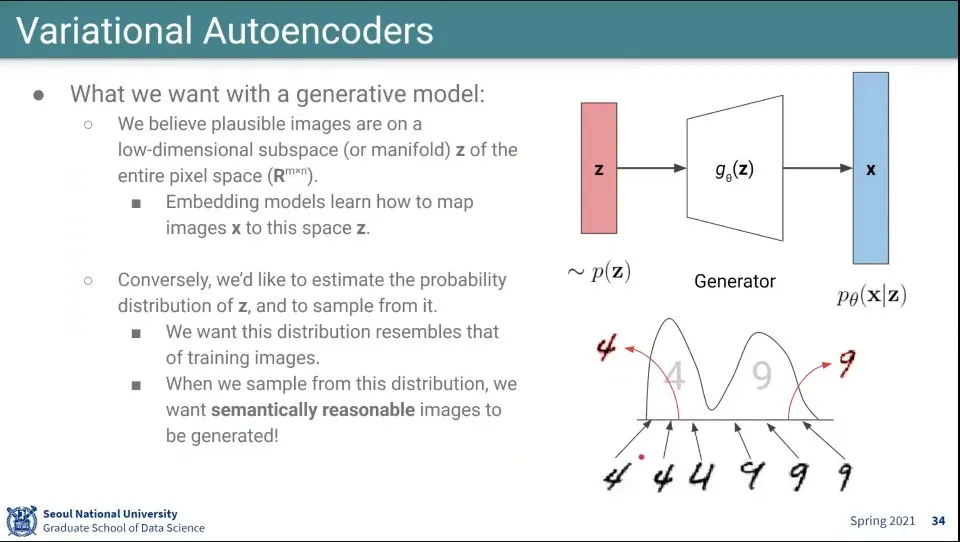
Z를 이용해서 Generator가 이미지를 만든다.
•
만일 아래 그림처럼 4, 9 손글씨 이미지가 있다면 그 분포를 학습한 후에, 그 분포에서 sampling해서 4나 9를 생성하는 것
•
어떤 잠재된 분포 에서 이미지를 생성하는 것을 가정하자.
◦
의 분포에 대해 제네레이터가 만들어내는 것을 모두 적분하면 어떤 분포 가 나온다는 전제
•
모든 가능한 에 대해 적분하는 것은 불가능하기 때문에 샘플링된 데이터로 근사함
•
우리가 가진 어떤 데이터셋의 likelihood를 높여주는 것이 목표
•
위의 목표를 위해 식을 위와 같이 설계
◦
정규분포로 가정해서 식을 전개했더니 squared loss가 나오는데, squared loss는 오른쪽 이미지와 같은 케이스가 있어서 제대로 안 됨. 사람이 보기에는 비슷하지만, squared loss는 차이가 큰 것
•
Variational Inference의 아이디어를 착용해서 Variational Autoencoder를 설계함
◦
앞서 정규 분포에서 를 하지 않고 를 함. x가 주어졌을 때 x에서 발견된 실제 이미지들을 의미상 관련 있는 것들을 구별할 수 있는 좋은 feature들을 잘 담고 있도록 Z의 분포를 학습을 시킴
◦
문제는 그런 분포를 모르기 때문에 라는 어떤 분포를 써서 그것을 근사 하도록 함. 이게 variational inference라는 통계학에서 사용한 아이디어를 차용함. 는 그 자체로서 정규분포는 아님
•
앞서와 달리 x를 잘 반영할 수 있게 를 모델링함
•
를 직접 만들지 않고, 그와 유사한 를 만들고 parametric optimization을 통해 를 근사하도록 함
•
최종적으로 알고자 하는 분포는 이고 그것을 maximize하는게 목표
•
위의 순서대로 식을 전개하면 가장 아래와 같은 식이 구해짐
◦
식을 전개할 때 베이즈룰도 쓰고, 분모 분자에 를 곱하고 하는 등
◦
KL은 KL-Divergence로써 두 확률 분포 간의 거리를 의미함
•
최종적으로 만들어진 에 대하여
◦
은 reconstruction에 대한 부분으로 앞의 첫 번째 try에서는 이 부분만 있었는데, 정규분포로 했더니 잘 안됐던거를 로 바꾼 것
◦
뒤의 두 함수를 추가한게 VAE의 핵심
◦
는 앞에 -가 붙었는데, 전체 식이 maximize가 되려면 이 부분은 minimize 되어야 함. 이것은 근사하는 확률 분포 가 목표로 하는 와 같아지도록 하는 것. (가까워질수록 값이 작아지므로)
◦
는 0보다 큰 값으로 lower bound로 쓰임. 이 부분은 별달리 설명이 불가능하고, VAE의 약점이 됨. 식의 오차가 됨
•
앞 페이지의 수식에 -를 붙여서 maximize 해야 했던 것을 minimize 하도록 변경함. (이러면 loss 함수가 됨)
•
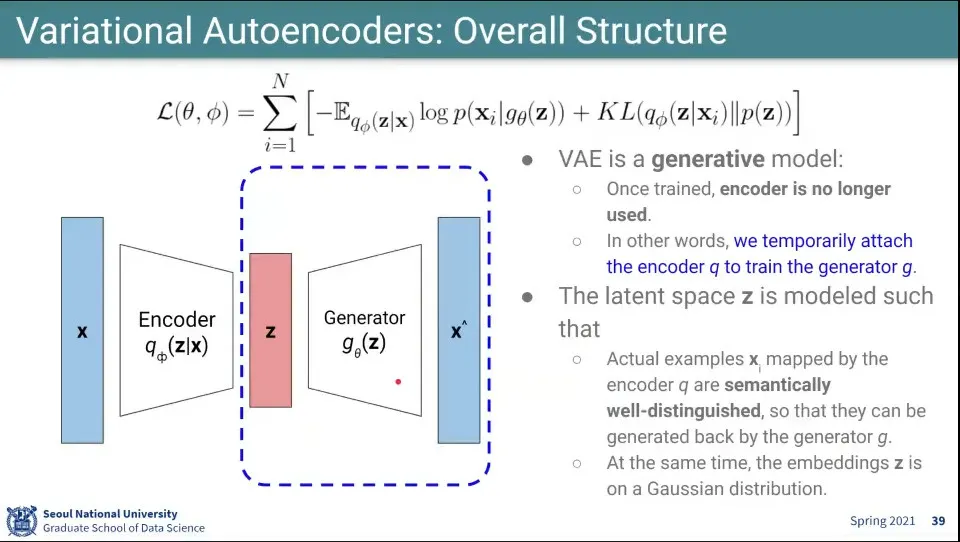
VAE는 generative model을 만드는게 목표이고, 그걸 위해 라는 분포를 만들고 그게 를 근사하도록 함
◦
그런데 이 가 마치 encoder와 같이 보임. input을 보고 Z를 만들어내는 역할을 하는게 결국
•
VAE는 AE와 달리 학습을 위해 Encoder가 필요하지만, 학습이 되고 나면 Generator 부분만 필요하기 때문에 Encoder는 사용하지 않고 Generator만 사용함
•
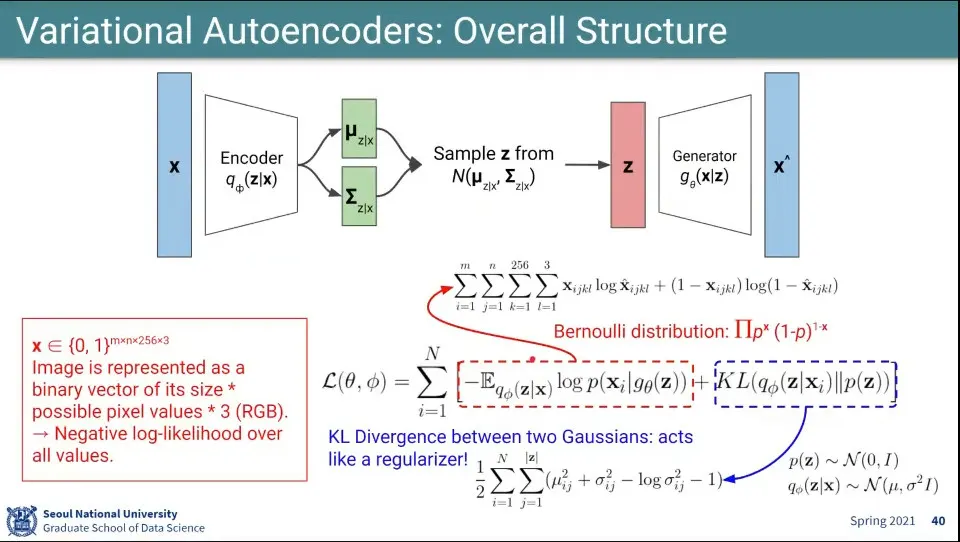
결국 아무 분포나 쓰지 못하고 정규 분포를 씀
1.
input으로부터 를 이용해서 와 를 뽑아냄
2.
그 2개를 이용해서 Z를 샘플링함
3.
그걸 이용해서 generation을 함
•
Loss 함수의 왼쪽 부분은 데이터의 likelihood를 표현함.
◦
데이터에 있었던 픽셀 단위의 이미지를 다시 reconstruct 하게 하는 역할을 함
•
Loss 함수의 오른쪽 부분은 2개의 분포 와 가 가까워지도록 함
•
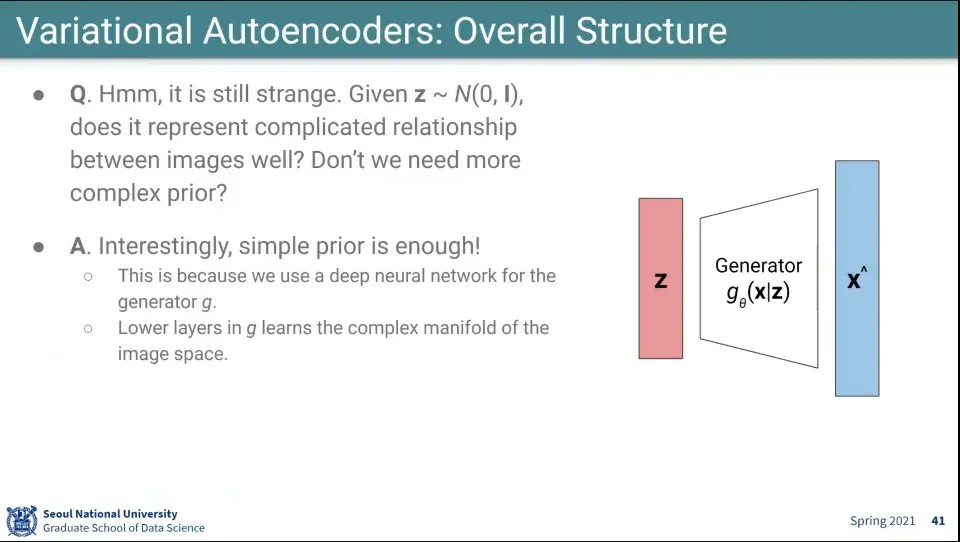
정규 분포만으로 복잡한 이미지를 다 구별할 수 있느냐?
◦
그게 가능한 것은 generator로 deep neural network를 쓰기 때문에 가능하다고 함
•
VAE 예시 - VAE가 학습한 Z를 그려본 결과
◦
숫자는 숫자별로 구분됨
◦
얼굴도 웃음과 얼굴 방향으로 잘 구분함
•
VAE 특징