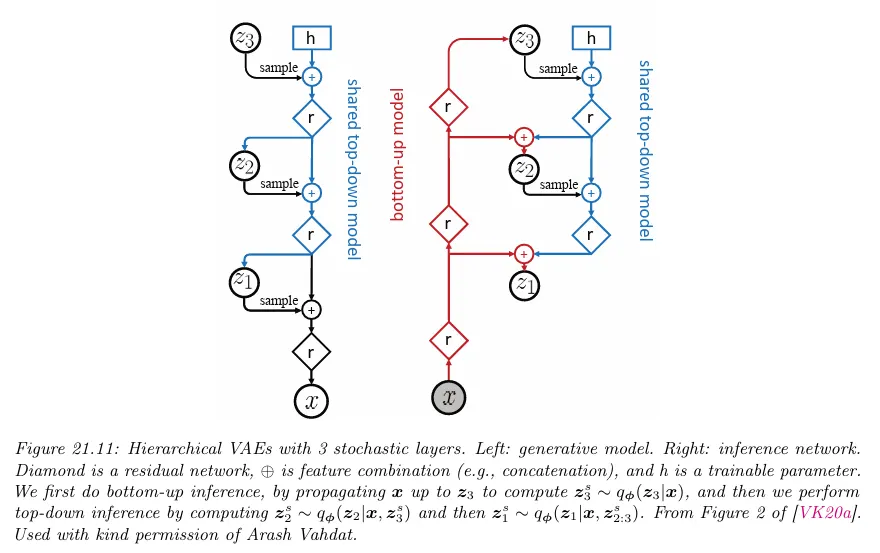
Hierarchical VAE
개 확률적 레이어를 갖는 hierarchical VAE(HVAE)를 다음과 같은 생성 모델로 정의한다.
위의 모델을 non-Markovian으로 만들어서 개선할 수 있다. 즉 이 이전 레벨 뿐만 아니라 모든 상위 레벨 확률적 변수 에 의존하도록 할 수 있다.
likelihood가 단순히 대신 임에 유의하라. 이것은 모든 선행 변수에서 모든 자식에 skip connection을 추가한 것과 유사하다
Inference
HVAE에서 추론을 수행하기 위해 다음 형식의 bottom-up inference 모델을 사용한다.
그러나 더 나은 접근은 다음 형식의 top-down inference 모델을 사용하는 것이다.
에 대한 추론은 의 bottom-up 정보를 상위 레이어의 top-down 정보와 결합한다.
위의 모델을 사용하여 ELBO는 다음과 같이 작성할 수 있다. (KL에 대한 체인 룰을 사용하여)
여기서
는 레이어 위의 근사 posterior 이다. (즉 의 부모)
top-down 추론 모델이 더 나은 이유는 주어진 레이어의 실제 posterior에 더 가깝기 때문이다.