•
이미지를 받아서 결과를 내보내 주는 함수 f(x)에 대한 접근
•
이미지의 픽셀 정보에 대해 어떤 Weight를 줘서 계산을 하자는 접근
•
수식으로 표현하면 다음과 같이 표현 됨
•
위 수식을 정리하면 다음과 같이 정의 됨. 입력 에 대해 가중치 를 적용하여 정답 를 계산 함.
•
width 32, height 32, channel 3인 이미지에 대해 10개의 label을 사용한다면 의 크기는 다음과 같이 계산 됨. 이때 는 계산하기 쉽게 1차원으로 변환한다.
◦
◦
◦
•
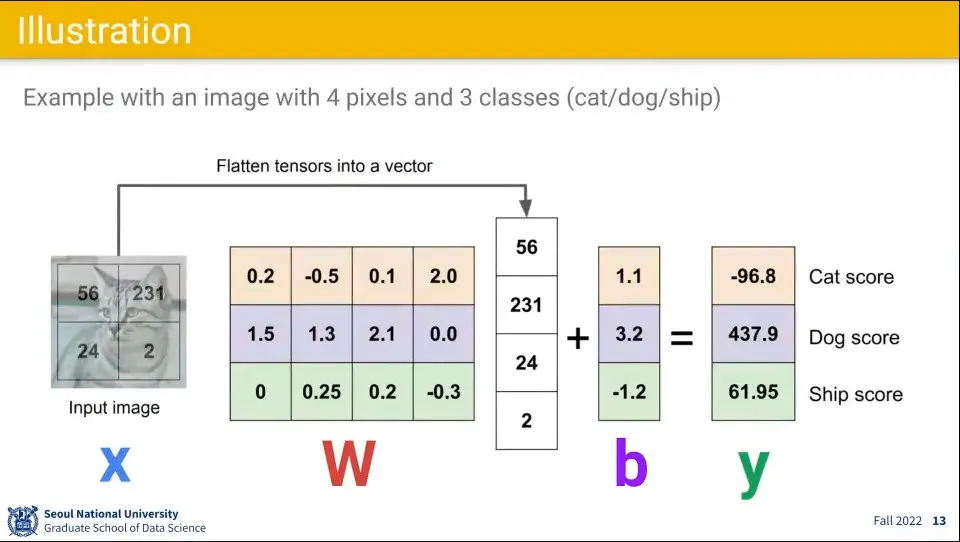
추가로 bias를 더해서 계산한다.
•
로 쓸 수도 있지만, bias는 상수이므로 아예 에 한 행, 에 한 열을 추가해서 계산할 수 도 있음.
◦
이렇게 하면 굳이 bias를 따로 추가하지 않고 로만 함수를 정의할 수 있는데, 다만 이러면 원래의 모습과 헷갈리므로 ‘를 추가해서 로 표기
◦
bias를 따로 더하지 않고 행렬과 벡터에 추가하면 계산이 깔끔해지며, 나중에 Neural Network 구성할 때도 간편하다.
•
이렇게 정의하면 모든 학습 데이터를 저장할 필요 없이 만 저장해 두면 계산이 가능
•
또한 의 크기만큼만 계산이 되기 때문에 모든 데이터에 대해 계산하는 것에 비해 계산량도 줄어듬.
•
위 함수의 계산 예
•
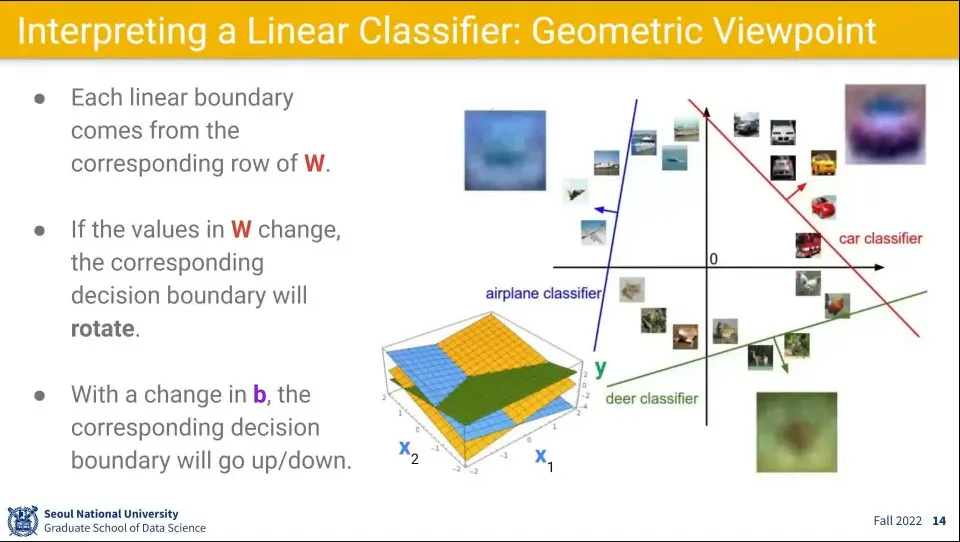
이 함수에 의한 계산은 공간을 각 라벨 별로 선형으로 분할하고 입력이 어느 영역에 해당하는지를 계산하는 것이 됨.
•
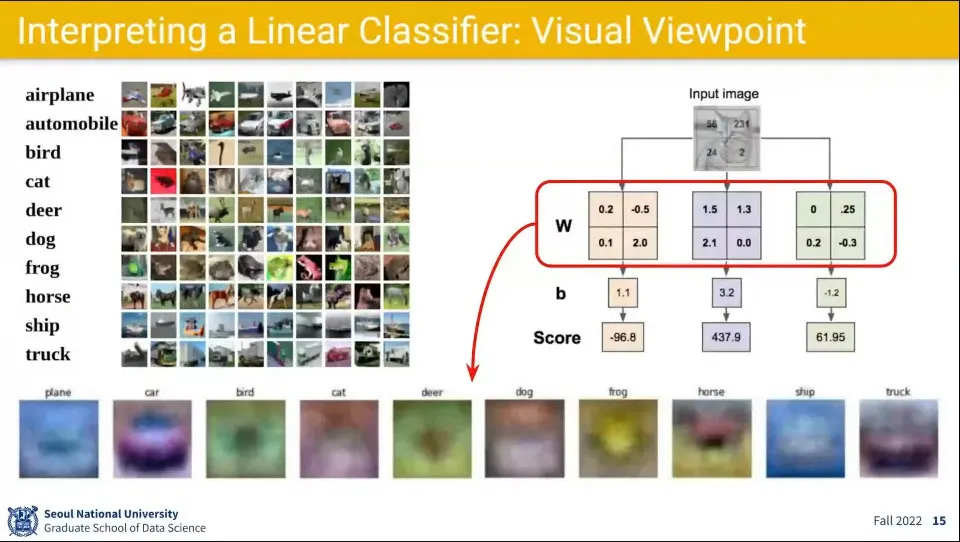
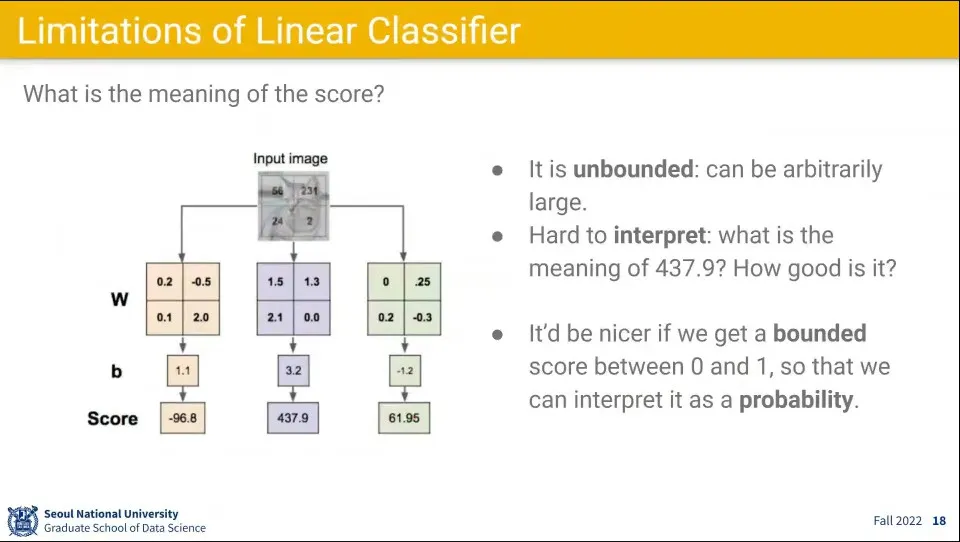
학습된 를 다시 그림으로 그리면 위 이미지의 아래쪽 흐릿한 그림처럼 표현 됨.
◦
어떤 것들은 실제 분류된 라벨과 비슷하게 보이는 반면, 어떤 것은 알아보기 어려움.
•
선형 함수를 이용해서 분류를 한 결과는 위 이미지와 같이 어떠한 값이 계산되는데, 이 값이 어떤 의미인지를 이해하기 어려움. 때문에 이것을 0-1사이의 확률값이 되도록 값을 조정해 줌.
•
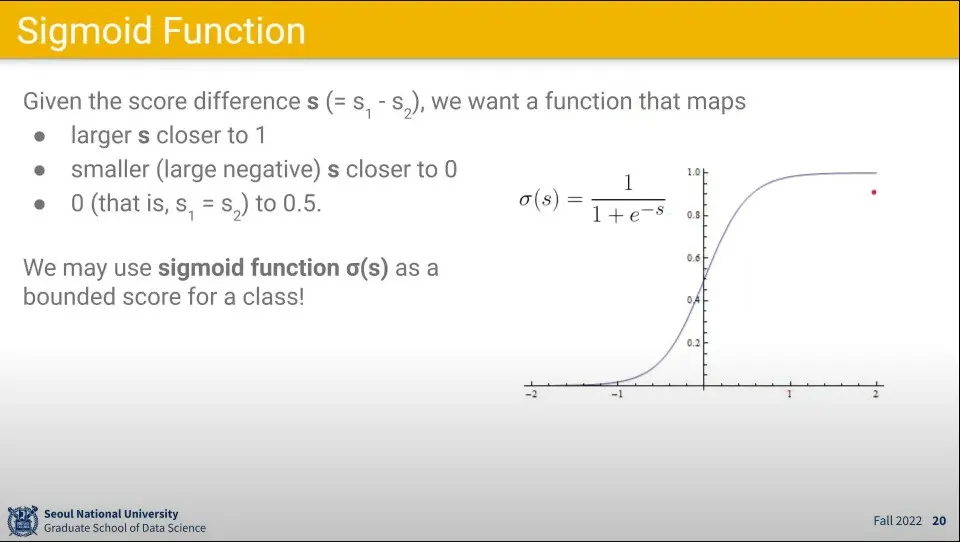
결과값은 대단히 큰 값이 나올 수도 있고, 음수가 나올 수도 있기 때문에 Sigmoid 함수를 이용해서 0-1 사이의 값이 나오도록 함
•
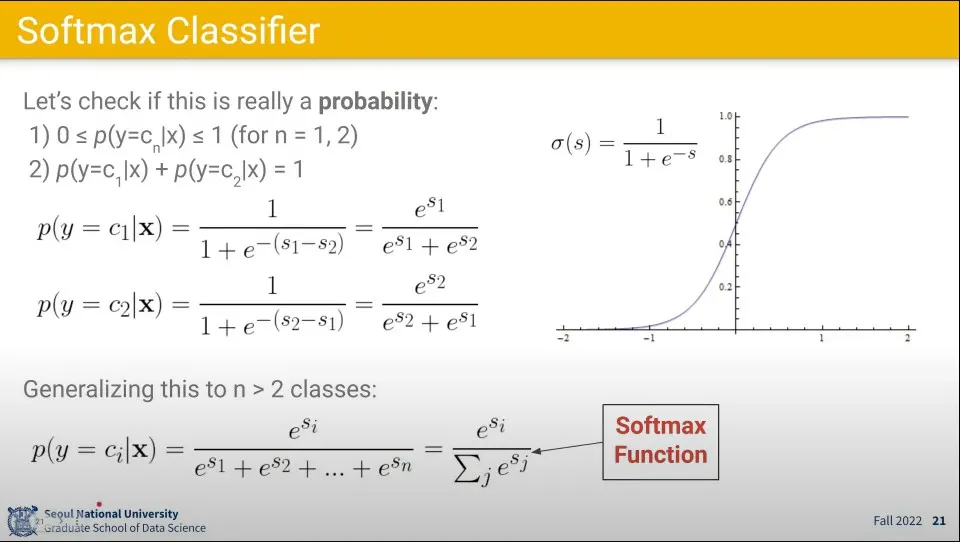
그 각 항목들에 대해 시그모이드 함수를 적용한 것들을 클래스별로 모아서 최종적으로 클래스 별 확률을 계산하도록 한 것이 Softmax 함수
•
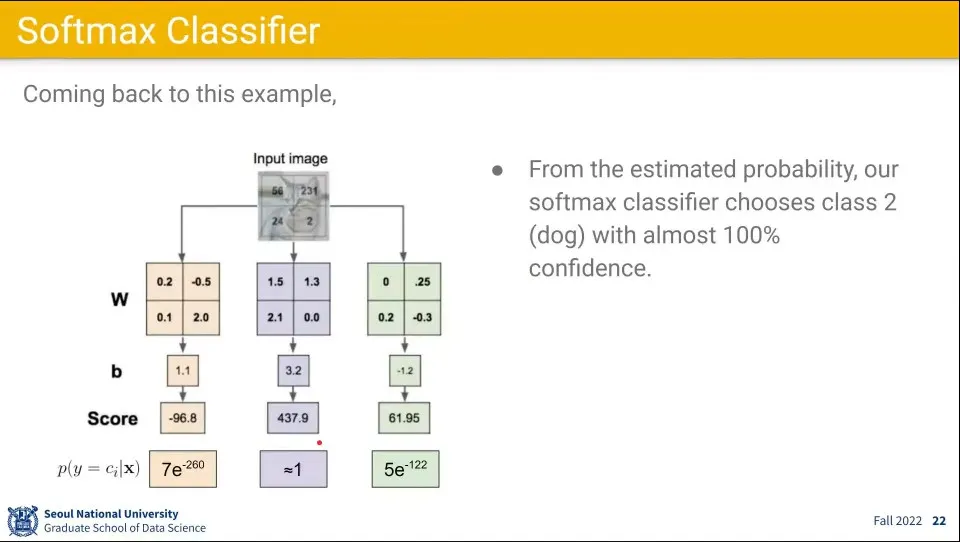
앞선 예에 소프트맥스 함수를 적용한 결과 예시.
◦
왼쪽과 오른쪽은 0에 가깝고 가운데 클래스일 확률이 1에 가까운 값이 나오기 때문에 훨씬 이해하기 쉽다.
•
머신러닝은 Data-Driven 접근이며 는 다음과 같은 절차에 의해 찾는다.
1.
사람은 모델 형식만 설계한다.
2.
를 랜덤으로 초기화 한다.
3.
학습 데이터()를 넣고 예측값()을 계산한다.
4.
예측값과 정답(의 차이를 비교하여 good/bad를 추정한다.
5.
그 차이가 줄어들도록 를 업데이트 한다.
6.
이 과정을 예측값이 정답과 같아질 때까지 반복한다.
•
예측과 정답를 비교하는 것을 Loss(손실) 함수를 통해 하며,
•
손실이 줄어들도록 를 업데이트 하는 것을 Optimization(최적화) 라고 한다.
•
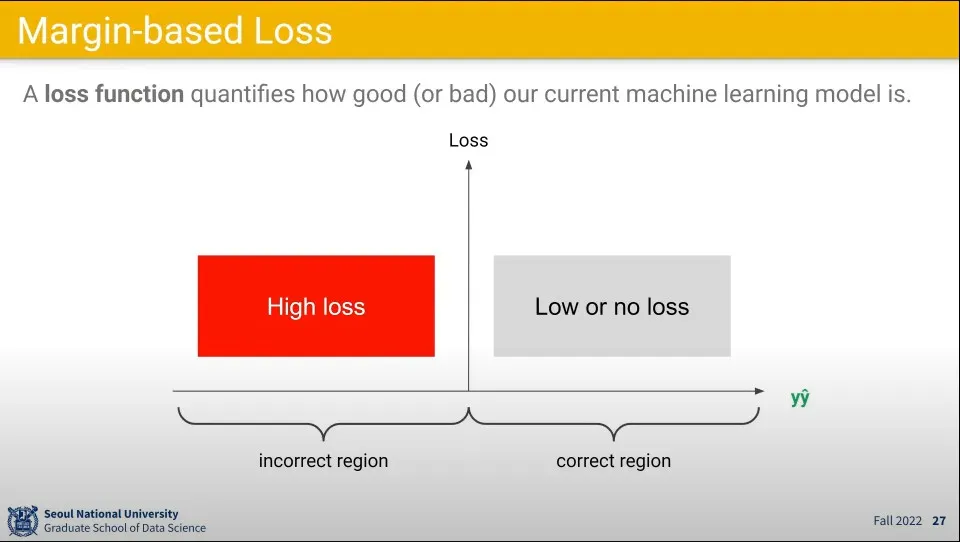
Loss 함수란 현재 모델이 얼마나 잘하고 있는지를 수치화하는 함수이다.
•
Loss 함수는 정답과 예측치를 입력으로 받는다.
•
Discriminative Setting하는 경우 정답()은 로 정의 함.
◦
따라서 예측()은 +1이 나오거나 -1이 나와야 함.
•
여기서 Margin-based loss는 예측과 정답을 곱해서 구한다.
◦
그 곱이 양수가 나오면 예측과 정답이 같다는 의미이고, 음수이면 틀렸다는 의미가 된다.
•
손실을 계산하기 위해 위 결과를 이용해서 곱의 결과가 양수이면 Loss가 낮다고 (혹은 없다)고 정의하고, 음수이면 Loss가 높다고 정의한다.
•
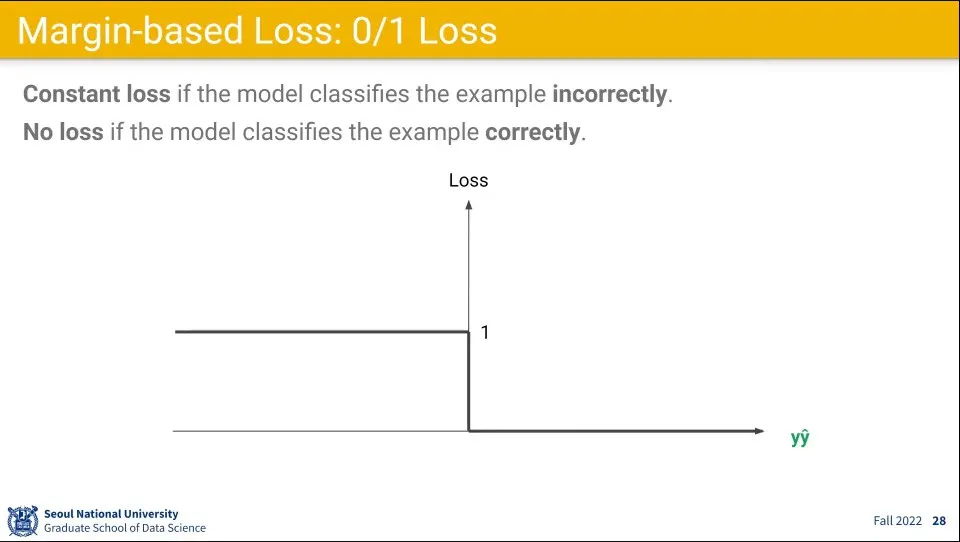
손실 함수를 맞았으면 Loss를 0, 틀렸으면 Loss를 1로 주는 식으로 할 수 있다.
◦
그러나 이 경우 0에서 미분이 안되기 때문에 문제가 된다. 그래서 몇가지 대체 함수를 사용한다.
•
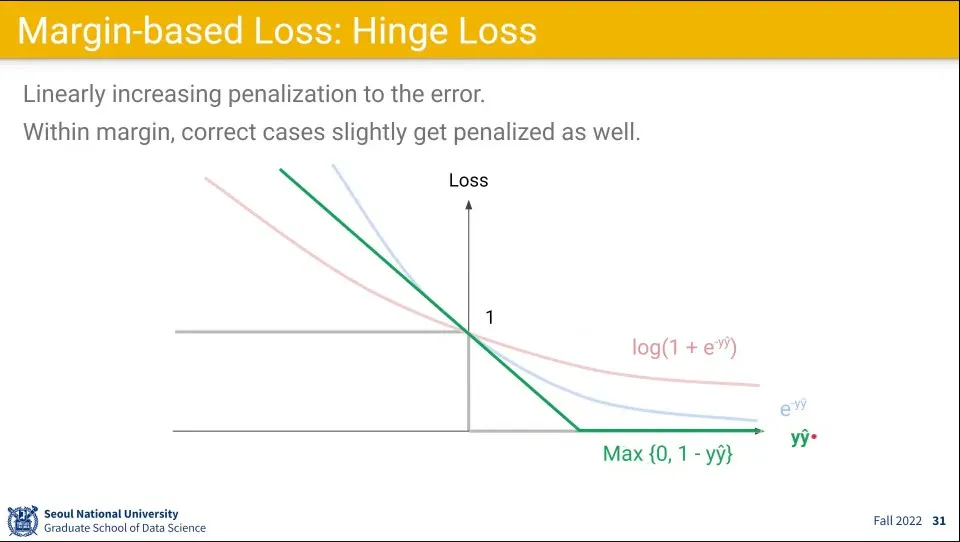
손실 함수로 사용할 만한 것은 3가지가 있다.
◦
◦
◦
이
▪
함수는 1에서 미분이 안되는데 이 점은 결정적인 순간이 아니기 때문에 문제가 없다.
▪
더불어 기울기가 일정하기 때문에 그냥 상수를 쓸 수 있다는 점에서 장점이 있다.
•
exponential loss는 위험도가 있다.
◦
값이 기하급수적으로 증가하기 때문에, 레이블이 잘못된 경우 문제가 된다.
•
Hinge loss와 Log loss가 많이 쓰이는데 Hinge loss는 SVM이고, Log loss는 선형회귀이다.
•
실제 사용은 Discriminative 보다는 Probabilistic Setting을 더 많이 사용한다.
•
손실 함수를 Probabilistic Setting하는 경우 정답()은 로 정의 함
◦
예측()은 0-1 사이의 확률 값으로 나옴.
•
만일 클래스가 2개 이상이면 정답()을 one-hot vector로 정의 함
◦
예측()은 softmax를 씌워서 전체 합이 1이 되게 함
•
Probabilistic Setting에서 손실 함수는 Cross Entropy를 많이 사용한다.
◦
일반적인 경우 위의 것을 사용하고 이진 문제인 경우 아래와 같이 할 수 있다.
•
정답이 one-hot vector로 주어지기 때문에 Cross Entropy의 경우 정답이 아닌 클래스는 0이 나온다. 때문에 정답인 클래스에 대해서만 계산이 이루어진다.
•
계산에 대해 를 씌우는데, 이것은 로그 함수의 모양 때문이다.
◦
0-1 사이의 구간이 설정되고, 정답에 가까울 수록 loss가 작고, 0에 가까울 수록 loss가 크게 나온다.
•
KL Divergence라는 손실 함수도 있는데, 두 확률 분포의 거리를 계산하는 개념.
•
Optimization은 어떤 제약 조건 하에서 가 최대가 되도록 하는 값을 구하는 문제로 생각할 수 있음
•
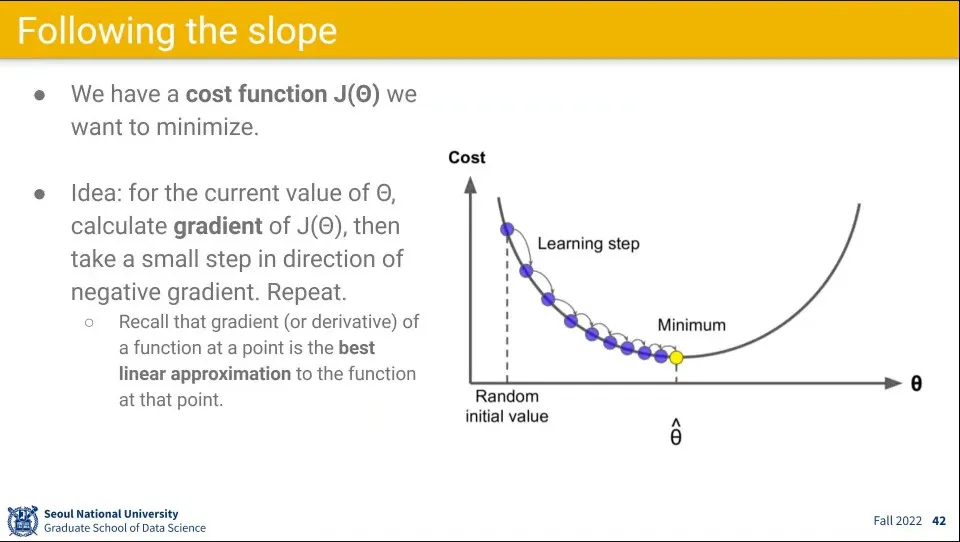
Optimization을 구하기 위해 slope를 내려가는 방식으로 구한다.
•
이를 구하기 위해 비용 함수 에 대해 gradient(미분값)를 구해서 파라미터를 업데이트 하는 방식으로 구한다.
•
Gradient Descent는 에 대해 미분하고 를 곱한 값을 기존 값에서 빼서 새로운 값을 구한다.
•
Gradient Descent는 몇 가지 문제가 있다.
◦
local optima에 빠질 수 있음.
◦
saddle point(말 안장 같은 생긴 지점. 한쪽 방향으로는 최고점인데, 다른 방향으로는 최저점이 됨)에서는 미분값이 0이 나오기 때문에 어느 방향으로도 움직일 수 없음.
◦
미분이 불가능한 점에서는 사용이 불가능
◦
local minimum에 가까워지면 느려짐
•
Gradient Descent를 개선한 Stochastic Gradient Descent(SGD)를 사용함.
◦
데이터셋 전체에 대해서 계산하는게 아니라 32, 64, 128개 등 샘플링한 것에 대해 계산.
◦
샘플링 갯수가 클수록 예측은 정확해지지만 계산이 느려짐, 작을수록 그 반대
◦
커지면 커질 수록 조금 늘어나는 것에 대해 효과는 작아짐
•
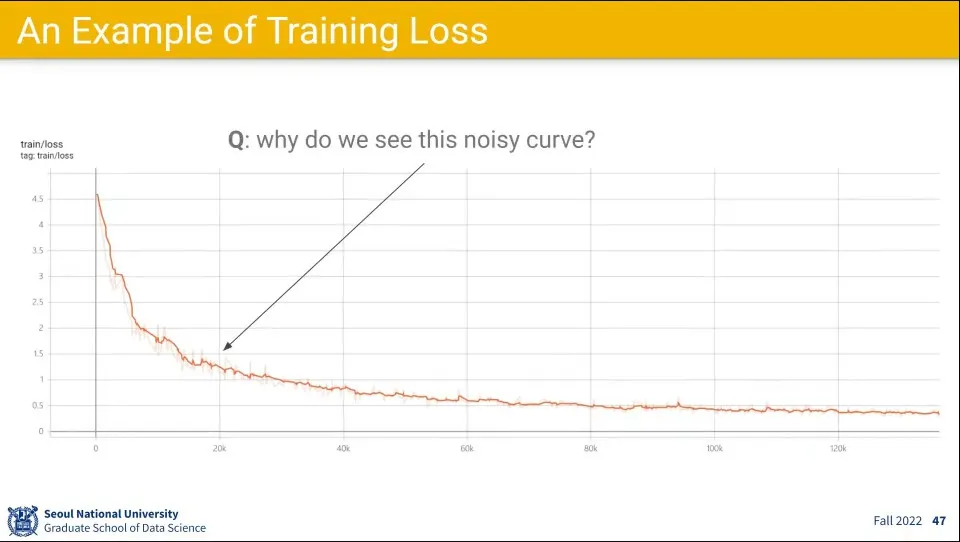
전체 데이터에 대해 Gradient Descent를 구하면 Loss는 계속 줄어들게 되지만, Stochastic Gradient Descent를 구하면 Loss가 일시적으로 튀는 구간이 나올 수 있음.