1 State estimation
인공 에이전트가 실시간 decision making을 믿을 만하게 수행하는데는 환경의 현재 상태를 아는 것이 핵심이다. state estimation에서 우리는 다양한 센서 소스(multi-modal 인지)에서 측정을 지속적으로 결합하여 현재 시점에서 시스템의 latent state를 추론하는데 초점을 맞춘다.
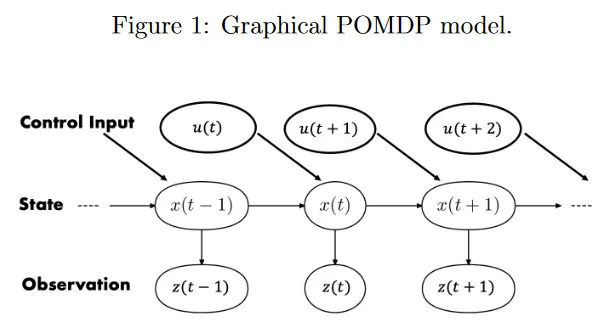
우선 확률론적 관점에서 이산 시간 동적 시스템을 살핀다. 그림 1은 graphical model 형식에서 Partially Observable Markov Decision Process(POMDP)을 시각화 한다.
유향 edge는 조건부 종속 관계를 나타낸다. 은 시간 에서 상태이고 이전 상태 에만 의존한다. 는 시간 에서 상태에 의존하는 센서 관측이다. 은 시간 에서 적용된 control input을 나타낸다. 예컨대 어떤 환경에 위치한 인공 에이전트의 상태는 position, orientation, linear, angular velocity 또는 이것들의 결합일 수 있다. 유사하게 상태에서 유도된 측정값은 로봇 position과 movement에 의존하는 환경의 카메라 이미지 또는 Lidar 측정일 수 있다.
측정과 control input이 알려지지만, hidden state 이력 는 알려지지 않는다. 우리는 시스템이 확률적 방법으로 진화하고 그 관찰도 확률적이라고 가정한다. 그러므로 우리는 상태 와 관찰 를 가능한 값으로 취할 수 있는 확률 변수 와 로 모델링한다. 표기의 단순화를 위해 를 로 작성한다. 유사하게 도.
state estimator의 목표는 이용 가능한 데이터(측정과 control input의 기록)과 상태 전이와 관찰에 대한 알려진 모델이 주어지면 상태 의 posterior 확률 분포를 계산 또는 근사하는 것이다. 구체적으로 측정과 control input의 시퀀스가 주어지면 상태가 취할 수 있는 모든 가능한 값에 확률을 할당하는 상태의 posterior 분포 를 알기를 원한다. posterior는 또한 시간 에서 state의 값에 대한 belief라고도 불리며 라고 표현된다. 확률적 공식화는 state에 대한 정확한 값을 제공하지 않지만 state가 무엇일 수 있는지데 대한 불확실성을 정량화할 수 있게 해준다.
그림 1의 graphical model을 사용하여 동적 시스템을 표현하여 state가 complete하다고 가정한다. 이 가정은 2가지 핵심 속성을 이끈다. 첫째, 우리는 시스템이 Markovian이라고 가정한다. 즉 현재 상태 는 전체 이력 이 아닌 오직 이전 상태 와 이전 control input 만 의존한다. 이것은 다음처럼 표현할 수 있다.
이것은 또한 transition model이라 부른다. 현재 에 (원문에는 나오는데 오타로 보임) 있고 control input 가 주어질 때 상태 로 전환될 가능성을 나타낸다.
들째, 현재 측정 값 는 오직 현재 상태 에만 의존한다고 가정한다. 즉 는 모든 이전 상태 와 측정 과 control input 에 조건부 독립이다. 이것은 다음처럼 표현할 수 있다.
이것은 또한 measurement model이라 부른다. 이것은 상태 가 주어질 때 측정값 가 얼마나 가능성 있는지를 나타낸다.
2 Bayes filter
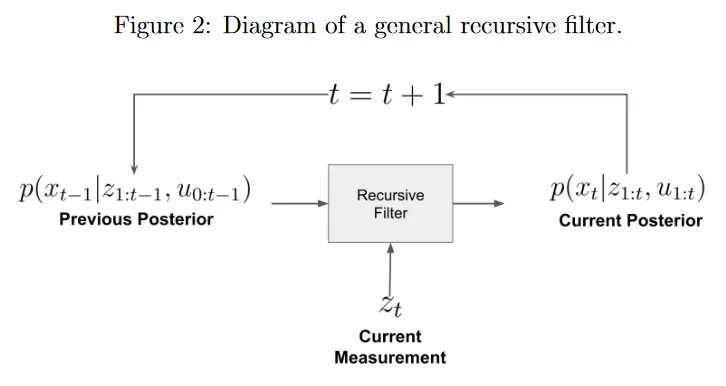
recursive filter는 상태 posterior를 추정하기 위해 지속적으로 새로운 측정을 ingests(섭취하다). 그림 2 참조. 각 time step 에서 우리는 이전 posterior 와 새로운 control input 과 새로운 측정값 만 사용하여 새로운 posterior 를 계산한다. 따라서 recursive filter의 복잡도는 시간 관점에서 상수이다. 이것은 이력의 크기에 의존하지 않고 실시간 추론에 적합하다.
2.1 Conditional probability review
결합 확률 분포를 로 분해할 수 있다. 여기서 와 는 확률 변수이다. 결합 분포가 또 다른 확률 변수 에 조건화되면, 조건을 와 같이 전달할 수 있다. 분포를 로 marginalize 할 수 있다. 이전과 유사하게 를 갖는다. 우리는 결합 분포를 2가지 별개의 방법으로 분해할 수 있다. 결과는 Bayes rule이다.
2.2 Derivation
이제 가장 단순한 recursive filter인 Bayes filter를 유도한다. 목표는 이전 posterior, 현재 측정값 , control input 와 전이와 측정 모델에만 의존하여 state posterior에 대한 recursive 표현식을 유도하는 것이다. 모델은 알려지고 와 를 계산하기 쉽다고 가정한다. 베이즈 룰과 측정의 조건부 독립은 다음을 제공한다.
그 다음 여전히 관찰의 전체 이력에 의존하는 우변에서 두 항을 단순화한다. 우선 분모를 보자. 에 대해 marginalizing하고 측정값의 조건부 독립을 사용하여 다음을 얻는다.
다음으로 이제 방정식 2에서 2번 나타나는 를 단순화할 수 있다. 에 대해 marginalizing하고 Markov 가정을 적용하여 다음을 얻는다.
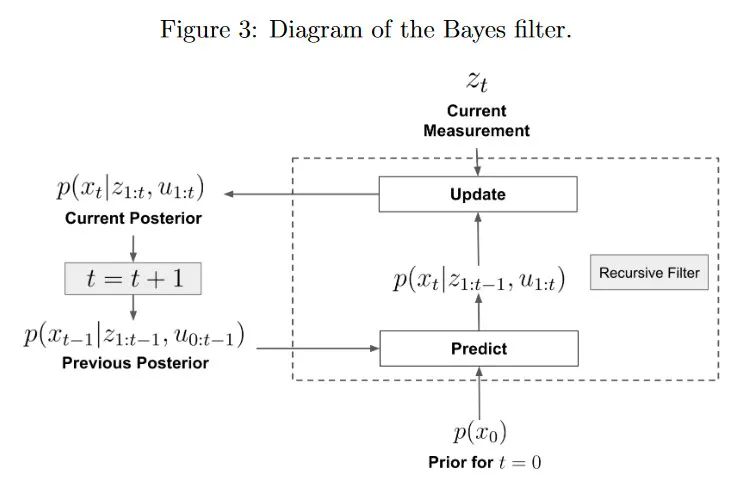
이제 Bayes filter의 전체 형식을 구성할 수 있다. 그림 3, 4 참조.
2 단계가 있다. prediction step에서 전이 모델 와 이전 posterior를 사용하여 현재 time step에서 state posterior 를 예측한다. 예측은 로 표현되고 이것은 새로운 정보 없이 의 분포에 대한 최선의 추측이다. 일 때, 이전 posterior는 아직 존재하지 않으므로 시작 시점 에서 의 분포에 대한 초기 믿음을 나타내는 prior 을 사용한다.
update step에서 새로운 측정값 를 통합하여 예측된 믿음을 다듬는다. measurement likelihood 는 예측된 가 주어질 때 관측 가 얼마나 가능성 있는지를 나타낸다. 따라서 update step에서 분자는 다음 2가지에 기반하여 확률을 특정한 에 할당한다. 1) 가 측정값 을 얼마나 잘 설명하는지 2) 동적 시스템 이전 posterior 추정치 에서 로 전이할 가능성. 분모는 단순히 업데이트된 posterior 분포가 합해서 1이 되도록 보장하는 정규화 상수이다. 믿음을 예측하고 업데이트한 후에 새로운 측정값 이 존재하는 한 에서 이 프로세스를 반복할 수 있다.
Bayes filter는 간단하고 모든 확률 분포에 일반화될 수 있다. 그러나 실제로 정규화 상수에 대한 적분을 계산하는 것이 종종 까다롭기 때문에 한계가 있다. 우리는 전체 확률 분포를 알아야 한다(예: 도메인의 모든 값에 대한 표 형식), 이것은 종종 이산 확률 변수를 다룰 때 또는 posterior 분포의 특정한 함수 형식(예: 가우시안)을 가정할 때만 가능하다. 따라서 Bayes filter를 특정한 요구사항과 가정을 갖는 다양한 시스템 집합에 적용할 수 있는 ‘확률적 템플릿’으로 생각하는 것이 더 유용하다.
2.3 Discrete Bayes filter
이제 와 는 유한한 수의 결과를 갖는 이산 경우에 대한 실제 구현을 살펴보자. 가 개의 가능한 값을 갖는 이산 확률변수라고 가정하자. 의 도메인은 이다. 유사하게 는 개 가능한 출력을 갖는 이산 확률 변수이고 의 도메인은 이다. 이산 Bayes filter에 대한 예측과 업데이트 방정식은 적분이 합으로 바뀌었다는 것만 제외하면 연속인 경우와 동일하다.
방정식 5는 시간 에서 전체 상태 posterior 분포를 나타내는 belief 벡터이다.
그러면 예측 단계는 행렬 곱으로 구현될 수 있다.
여기서 는 전이 확률을 나타낸다.
유사하게 업데이트 단계는 행렬 곱으로 구현될 수 있다.
여기서 은 측정 모델 확률을 나타낸다.
방정식 9의 (원문에는 5로 나오는데 오타인 듯) 분모에서 은 각 항은 인 벡터이고 unnormalized 확률을 합하는데 사용된다.
무한히 큰 상태 공간을 cumulative posterior를 나타내는 단일 확률 값을 사용하여 유한한 수의 region으로 분할하여 연속 확률 변수에 이 접근 방식을 적용할 수도 있다. 연속 상태 공간을 이산화한 결과는 histogram filter이다.
3 Kalman filter
초기에 상태 전이 모델 과 측정 모델 이 확률 분포로 표현되는 것을 보았다. 이것은 Bayesian 관점이다. 전이와 측정 모델은 동적 시스템 관점에서도 볼 수 있다. 여기서 방정식 11은 동적 모델이고 방정식 12는 측정 모델을 나타낸다.
은 상태가 시간에 걸쳐 에서 로 어떻게 진화하는지를 포함하는 시스템의 dynamics이다. 유사하게 는 상태 를 해당하는 관찰에 매핑하는 함수이다. 와 는 각각 dynamical 시스템에서 자연스럽게 드러나는프로세스 노이즈(시스템에서 랜덤 교란)와 측정 노이즈(센서 내부의)이다. 우리는 dynamics와 measurement 모델 뿐만 아니라 noise 통계량 ()도 알려진다고 가정한다. 동적 시스템 방정식은 그림 1에서 graphical 모델과 동일하며, 우리는 상태가 완전하다고 가정한다. 는 와 에만 의존하고 는 에만 의존한다.
3.1 Gaussian distributions
이 multivariate Gaussian distribution(normal 분포라고도 함)에서 샘플링된 확률 벡터라고 하면, 라고 할 수 있다. 여기서 은 mean vector이고 은 양의 준정부호 covariance matrix이다(단변량 경우의 분산과 유사하다). 해당하는 probability density function(PDF)는 다음과 같다.
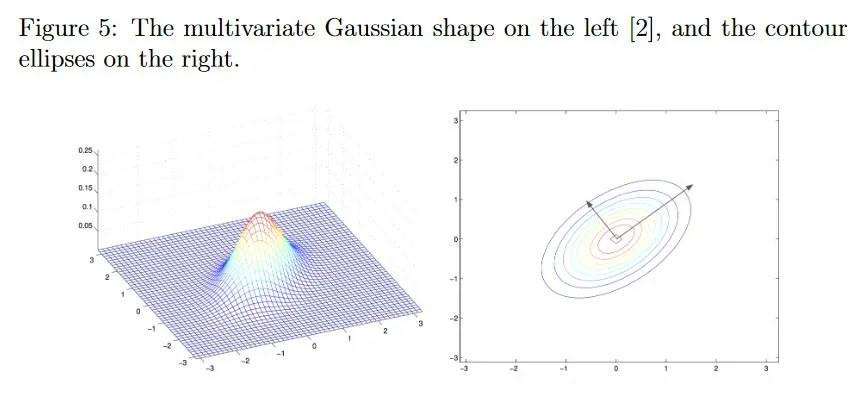
그림 5는 분포와 레벨 집합의 물리적 형태를 그린다. 여기서 확률은 각 타원을 따라 일정하다.
가 각 방향에서 분포의 ‘spread’를 나타내는 것을 볼 수 있다. 의 eigenvector는 축의 방향이고 scaling은 eigenvalue에 기반한다. 큰 eigenvalue는 해당 eigenvector의 방향으로 높은 불확실성을 나타내고 작은 eigenvalue는 그 반대이다. 공분산 행렬은 분포 신뢰도를 나타낼 뿐만 아니라 간접적으로 상태의 다른 성분 사이의 correlation을 간접적으로 포착하며, 이것은 추정에 유용하다. 다변량 가우시안에 대한 더 상세한 내용은 CS 229 노트와 Berkeley CS 189 노트 참조.
Kalman filter는 Bayes filter를 linear Gaussian system에 적용한 것이다. 이름이 암시하듯이 linear-Gaussian system은 두 개의 핵심 가정을 한다. 첫째, 관련된 모든 확률 변수(예: state, measurement, posterior, noise)가 다변량 가우시안이다. 둘째, 모든 변수가 부모 변수에 대해 선형이다. 과 는 선형( 형식에서)이다. 방정식 14와 15는 linear-Gaussian system 모델을 나타낸다.
우리는 프로세스 노이즈와 측정 노이즈가 zero-mean의 Gaussian white noise이라고 가정한다. 즉 이고 이고, 인 에 대해 이고 이다. 초기 조건 즉, prior는 으로 표현된다. 또한 모든 에 대해 이고 이고 모든 에 대해 이라고 가정한다.
Kalman filter는 linear-Gaussian system으로 제한되지만 연속 확률 변수와 벡터(무한히 많은 출력)을 효율적으로 다룰 수 있게 해준다. 이것은 와 만 가지면 전체 확률 분포를 갖기 때문이다. 따라서 Bayes filter에서처럼 전체 분포 (모든 가능한 에 대해)를 예측하고 업데이트하는 대신, 각 시간 단계에서 평균 벡터와 공분산 행렬만 예측하고 업데이트 하면 된다. 이것은 닫힌 형식 방정식으로 할 수 있다. 여기서 Kalman filter 방정식만 제시하고 이를 해석하여 기본 직관을 설명한다. 평균과 공분산에 대한 기대값 정의를 적용하는 확률적 관점에서 또는 mean-squared error의 측면에서 최적의 linear unbiased estimator로써의 최적화 관점에서 수많은 파생이 온라인에 있다.
Bayes filter와 유사하게 Kalman filter는 예측과 업데이트 단계로 구성된다.
예측 단계에서는 이전 posterior와 시스템의 프로세스 모델에 대한 지식을 바탕으로 예측된 posterior 의 평균과 공분산을 계산한다.
이전 posterior는 이다. 평균 을 예측하기 위해 을 방정식 14에 연결하여 방정식 16을 얻는다. 방정식 14의 노이즈 항 가 zero-mean이므로 에 영향을 주지 않는다. 방정식 17에서 공분산 예측을 유도하기 위해, 우선 공분산 를 갖는 확률 변수 가 주어지면 는 사실을 이용한다. 그 다음 시스템이 시간에따라 진화하면서 발생할 수 있는 모든 교란을 고려하기 위해, 프로세스 노이즈의 공분산 를 추가한다. 모든 공분산 행렬이 양의 정부호이므로 이 합은 증가된 불확실성을 나타내는 더 큰 예측 공분산 값을 이끈다. 까지의 데이터만으로 시간 에서 상태에 관한 예측을 하고 있기 때문에, 상태 분포에 대한 신뢰도가 낮아진다.
업데이트 단계에서 예측된 평균과 공분산을 새로운 측정값 를 사용하여 조정한다. 평균과 공분산 업데이트 방정식은 다음과 같다.
방정식만으로도 업데이트 단계가 예측 단계 보다 더 까다로운 것을 볼 수 있다. 평균 업데이트부터 시작하면, 는 센서 측정값이고 은 예측된 측정값이다(state가 예측한 대로라면, 이는 우리가 얻었을 측정값이다). 따라서 measurement residual 은 innovation이라 부르며 예측된 측정량이 센서를 통해 얻은 실제 관찰과 얼마나 차이가 있는지를 나타낸다. 그러므로 평균 업데이트는 예측된 평균 을 이 measurement residual와 조정하고 조화시키려고 시도한다. 이것은 Kalman Gain 를 통해 이루어진다. 는 우리의 추정을 얼마나 보정해야 하는지 알려주는 ‘weighting factor’로 볼 수 있다. 이제 를 다음과 같이 다시 작성할 수 있다.
이제 우변의 분수를 두 가지 극단적인 경우로 분석하자. 첫 번째로, 이 0으로 접근하는 경우는 측정 노이즈가 거의 없다고 믿는 경우를 의미한다. 이 분수는 1에 가까워지고 는 단순히 가 되며, 따라서 가 된다. 노이즈가 없다는 것은 측정값 가 매우 정확하다는 것을 확신하며, 측정 모델을 단순히 반전하여 실제 상태를 얻을 수 있다. 게다가 공분산은 으로 업데이트 되어 상태의 값에 대한 높은 신뢰도를 나타낸다.
두 번째 경우는 가 0에 접근하는 경우로, 이는 프로세스 노이즈가 거의 없다는 것을 의미한다. 이 경우 분수는 0에 접근하고 이 되며, 업데이트된 평균은 이고 업데이트된 공분산은 이 된다. 이것은 시스템에 교란이 없기 때문에 프로세스 모델만으로 상태를 시간에 따라 전파하는데 충분하여 측정값을 전혀 통합할 필요가 없다는 것을 의미한다(filter를 좋은 prior로 초기화한다고 가정할 때).
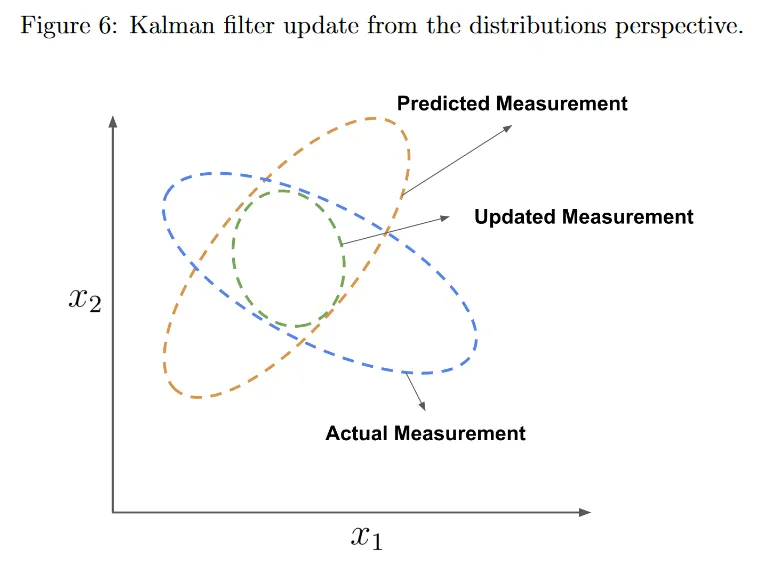
실제로는 이 두 경우 모두 발생하지 않으며, filter는 실제 측정과 예측된 측정을 모두 사용하여 평균과 공분산을 업데이트하려고 한다. 2d 상태의 경우에 대해 그림 6 참조.
그림 6에서 축은 상태의 컴포넌트이다. 우리는 top-down으로 분포를 본다. 오렌지색 타원은 으로 주어지는 예측된 측정에 대한 분포를 나타낸다. 파란색 타원은 로 주어지는 실제 측정에 대한 분포를 나타낸다. Kalman filter는 이 분포 모두를 곱하여 두 분포 모두에서 가 가장 가능성 있는 겹치는 region을 찾는다(을 떠올려라). 이것은 업데이트된 분포가 되며, 녹색 타원으로 표시되는 로 주어지는 또 다른 가우시안이다. 겹치는 부분을 취하기 때문에 업데이트된 분포가 두 부모 분포와 비교하여 더 작다는 것에 유의하라. 예측 단계에서는 공분산(불확실성)이 증가하지만, 업데이트 단계에서는 새로운 측정 를 사용하여 공분산을 감소시킨다. 따라서 공분산은 예측과 업데이트 단계 후에 증가와 감소를 반복한다. 전체적으로 공분산은 수렴할 때까지 감소한다.
4 Extended Kalman filter (EKF)
앞서 언급한 Kalman filter는 linear-Gaussian system에 대해 성립한다. 선형 프로세스와 측정 모델은 예측되고 업데이트된 분포 또한 가우시안이라는 것을 보장한다.
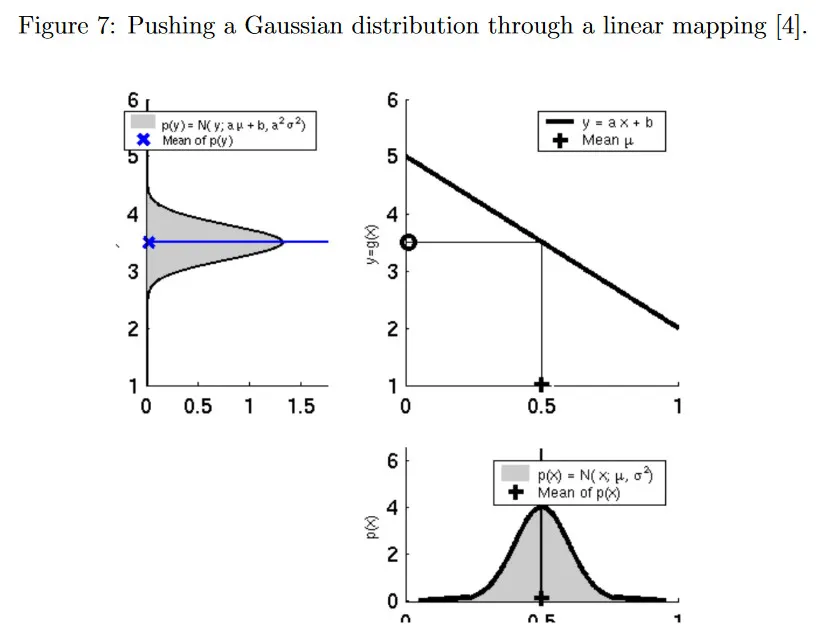
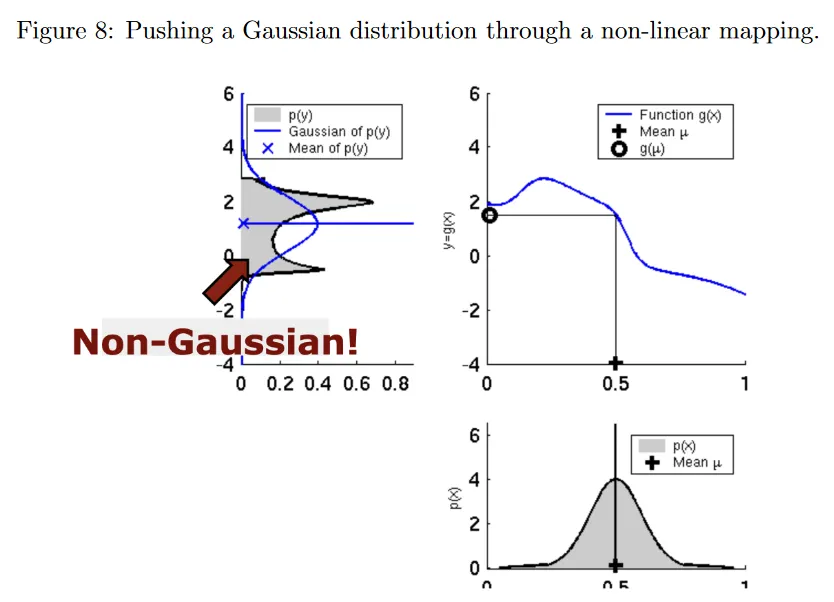
그림 7은 확률 변수 에 대한 선형 매핑을 적용해도 변환 후 결과가 여전히 가우시안 분포임을 보인다. 반면 그림 8은 비선형 매핑을 적용하면 비가우시안 분포가 되어 이전 예측과 업데이트 방정식을 더는 적용할 수 없음을 보인다.
extended Kalman filter는 비선형 dynamics와 measurement 함수를 시간 에서 입력에 관해 선형화하여 처리한다.
이것을 와 을 주위에서 1차 테일러 급수 전개를 통해 수행할 수 있다.
그러면 예측 단계는 다음이 된다.
업데이트 단계는 다음이 된다.
와 는 에 대한 비선형 dynamics와 measurement 모델의 야코비안이다.