Products of Experts(PoE)
Products of Experts(PoE)는 여러 전문가(Experts) 모델을 결합하여 복잡한 분포를 모델링하는 방법이다. 이것은 개별 전문가 모델이 각각 특정 데이터의 측면을 포착하고, 이 전문가들의 결합을 통해 보다 정교하고 표현력 있는 모델을 구축하는 것을 목표로 한다. PoE는 각 전문가의 예측을 곱해서 최종 모델의 분포를 생성한다.
예컨대 각 전문가 가 데이터 에 대한 확률 분포 를 정의한다고 할 때 PoE는 다음과 같은 결합 분포를 구한다.
만일 정규화 상수 를 안다면 다음과 같이 작성할 수 있다.
PoE는 전문가들의 결합 분포를 학습하는 것이 계산적으로 어렵고, 정규화 상수를 계산하는 것이 어렵다는 문제가 존재한다.
Mixture of Experts(MoE)
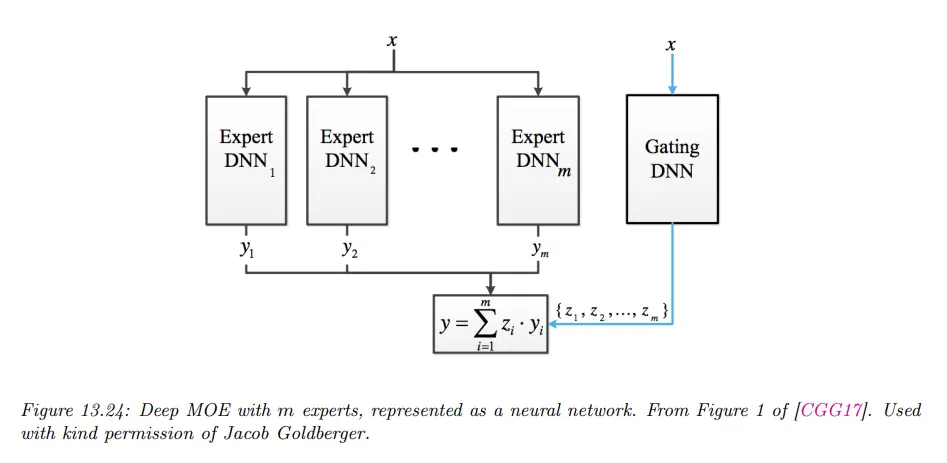
Mixture of Experts(MoE)는 여러 전문가(Experts)를 혼합한다는 점에서 PoE와 유사하지만, 전문가들의 곱이 아닌 가중 평균을 사용한다는 점에서 차이가 있다. 즉 MoE는 다음과 같이 정의되는 모델이다.
이때 각 전문가에 대한 가중치 는 별도의 Gate Network를 통해 계산되며, Gate Network는 입력에 대해 각 전문가의 가중치를 계산하여 최종 예측이 특정 데이터에 대해 가장 적합한 전문가의 출력을 반영하도록 학습된다.
예컨대 가우시안 조건부 혼합 모델 에 대해 다음과 같이 정의할 수 있다.
여기서 는 -번째 가우시안의 평균을 예측하고, 는 그것의 분산 항을 예측하고, 는 사용할 수 있는 혼합 성분을 예측한다.
gating 함수와 expert를 모두 DNN으로 만들면 결과 모델은 mixture density network(MDN) 또는 deep mixture of experts라고 한다.
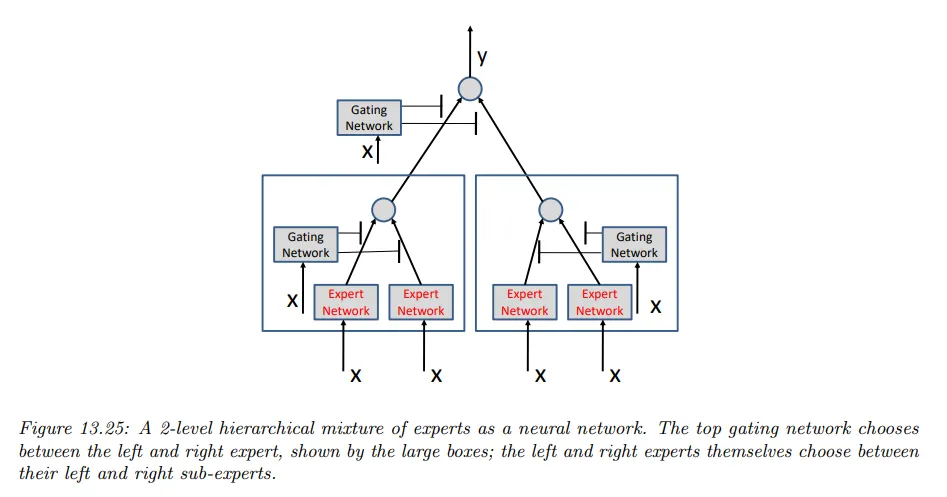
각 expert가 그 자체로 MoE 모델인 경우, 결과 모델은 hierarchical mixture of experts(HME)라고 부른다. 아래 그림은 2단계 계층 구조의 예이다.
레벨의 HME는 깊이 의 결정 트리의 soft 버전으로 생각할 수 있다. 여기서 각 예는 tree의 모든 branch를 통과하고, 마지막 예측은 가중 평균(weighted average)이다.
Sample Code
다음과 같이 Expert와 GateNetwork를 각각 정의하고 이를 모아 MoE 모델을 구성할 수 있다.
게이트 네트워크와 개별 전문가들에게 입력을 전달해서 결과를 얻고 게이트 네트워크의 가중치와 개별 전문가들의 출력을 결합해서 최종 결과를 출력한다.
# Define the expert models
class Expert(nn.Module):
def __init__(self, input_dim, output_dim):
super(Expert, self).__init__()
self.fc1 = nn.Linear(input_dim, 32)
self.fc2 = nn.Linear(32, output_dim)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = self.fc2(x)
return x
# Define the gate network
class GateNetwork(nn.Module):
def __init__(self, input_dim, num_experts):
super(GateNetwork, self).__init__()
self.fc1 = nn.Linear(input_dim, 16)
self.fc2 = nn.Linear(16, num_experts)
self.softmax = nn.Softmax(dim=1)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = self.softmax(self.fc2(x))
return x
# Define the MoE model
class MoE(nn.Module):
def __init__(self, input_dim, output_dim, num_experts):
super(MoE, self).__init__()
self.experts = nn.ModuleList([Expert(input_dim, output_dim) for _ in range(num_experts)])
self.gate = GateNetwork(input_dim, num_experts)
def forward(self, x):
gate_outputs = self.gate(x)
expert_outputs = torch.stack([expert(x) for expert in self.experts], dim=2)
moe_output = torch.sum(gate_outputs.unsqueeze(2) * expert_outputs, dim=1)
return moe_output
Python
복사
정의한 전문가와 gate network를 이용하여 다음과 같이 학습할 수 있다.
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
# Hyperparameters
input_dim = 10
output_dim = 1
num_experts = 3
learning_rate = 0.001
num_epochs = 10
batch_size = 32
# Create the MoE model
moe_model = MoE(input_dim, output_dim, num_experts)
# Loss and optimizer
criterion = nn.MSELoss()
optimizer = optim.Adam(moe_model.parameters(), lr=learning_rate)
# Sample data
X_train = np.random.rand(1000, input_dim).astype(np.float32)
y_train = np.random.rand(1000, output_dim).astype(np.float32)
# Training loop
moe_model.train()
for epoch in range(num_epochs):
permutation = np.random.permutation(X_train.shape[0])
X_train = X_train[permutation]
y_train = y_train[permutation]
for i in range(0, X_train.shape[0], batch_size):
X_batch = torch.tensor(X_train[i:i+batch_size])
y_batch = torch.tensor(y_train[i:i+batch_size])
# Forward pass
outputs = moe_model(X_batch)
loss = criterion(outputs, y_batch)
# Backward pass and optimization
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')
# Evaluate the MoE model
X_test = torch.tensor(np.random.rand(200, input_dim).astype(np.float32))
y_test = torch.tensor(np.random.rand(200, output_dim).astype(np.float32))
moe_model.eval()
with torch.no_grad():
outputs = moe_model(X_test)
loss = criterion(outputs, y_test)
print(f'Test Loss: {loss.item():.4f}')
Python
복사