Abstract
지금까지 가장 높은 정확도의 object detector는 R-CNN에 의해 대중화된 two-state 접근에 기반한다. 여기서 classifier는 희소한 후보 object location 집합에 적용된다. 반면 가능한 object의 location에 regular이고 dense sampling을 적용하는 one-stage detector는 더 빠르고 더 간단하다는 잠재적인 이점이 있지만 지금까지 two-stage detector의 정확도에 뒤쳐진다. 이 논문에서 이러한 현상의 원인을 조사한다. 우리는 dense detector 학습 중 마주치는 극단적인 foreground-background 클래스 불균형이 주요 원인임을 발견했다. 우리는 이 클래스 불균형을 해결하기 위해 잘 정의된 예제에 할당된 loss를 낮추는 방식으로 표준 cross entropy loss를 재구성할 것을 제안한다. 우리의 새로운 focal loss는 학습을 hard example의 희소 집합에 집중 시키고, 학습하는 동안 방대한 수의 쉬운 negative들이 detector를 압도하는 것을 방지한다. 우리 loss의 효율성을 평가하기 위해 우리는 RetinaNet이라 부르는 간단한 dense detector를 설계하고 학습했다. 우리의 결과는 focal loss로 학습한 RetinaNet이 기존의 one-stage detector의 속도와 일치하면서도 모든 기존 최첨단 two-stage detector의 정확도를 능가하는 것을 보인다. 코드는 참조.
1. Introduction
현재 최첨단 object detector는 two-stage, proposal-driven 메커니즘에 기반한다. R-CNN 프레임워크에서 대중화된 것과 같이 첫 단계에서는 희소한 후보 object location의 집합을 생성하고, 두 번째 단계에서는 convolutional neural network를 사용하여 각 후보 location을 foreground class 또는 background 중 하나로 분류한다. 일련의 발전을 통해 이 two-stage 프레임워크는 도전적인 COCO 벤치마크 챌린지에서 지속적으로 최고의 정확도를 달성한다.
two-stage detector의 성공에도 불구하고 자연스러운 질문은 이것이다. 간단한 one-stage detector로 유사한 정확도를 달성할 수 있을까? one stage detector는 object location, scale, 종횡비에 대해 regular, dense sampling에 적용된다. YOLO나 SSD 같은 one-stage detector의 최근 작업은 유망한 결과를 보여주며, 최첨단 two-stage 방법의 10-40% 내의 정확도로 더 빠른 detector를 산출했다.
이 논문은 한계를 더욱 확장한다. 우리는 처음으로 Feature Pyramid Network(FPN) 이나 Mask R-CNN, Faster R-CNN의 변종 같은 더 복잡한 two-stage detector 의 최첨단 COCO AP와 일치하는 one-stage detector를 제시한다. 이 결과를 달성하기 위해 우리는 학습하는 동안 클래스 불균형을 one-stage detector가 최첨단 정확도를 달성하는데 방해하는 주요 장애물로 식별하고, 이 장벽을 제거하는 새로운 loss 함수를 제안한다.
R-CNN-like detector에서는 two-stage 후보와 샘플링 휴리스틱을 통해 Class 불균형을 해결한다. proposal stage(예: Selective Search, EdgeBoxes, DeepMask, RPN)에서는 후보 객체 location의 수를 빠르게 줄이고(예: 1-2k), 대부분의 background 샘플을 필터링한다. 두 번째 분류 단계에서 fixed foreground-to-background ratio(1:3)이나 online hard example mining(OHEM) 같은 샘플링 휴리스틱을 수행하여 foreground와 background 사이의 관리 간으한 균형을 유지한다.
반면 one-stage detector는 이미지 전체에 걸쳐 regulary 샘플링된 훨씬 큰 후보 객체 location 집합을 처리해야 한다. 실제로 이것은 종종 공간 position, scale, 종횡비를 densely 커버하는 100k location을 열거하는 것과 같다. 유사한 샘플링 휴리스틱을 적용할 수 있지만, 학습 절차가 여전히 쉽게 분류되는 background 예제에 의해 압도되기 때문에 비효율적이다. 이러한 비효율성은 object detection에서 전통적인 문제로, 일반적으로 bootstrapping이나 hard example mining 같은 기법을 통해 다뤄진다.
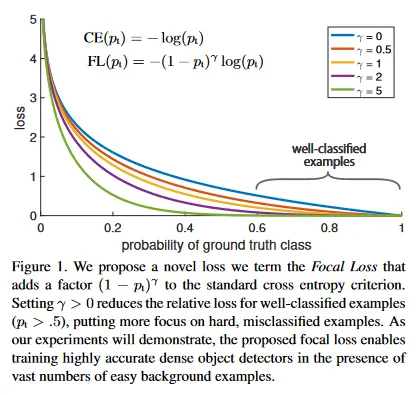
이 논문에서 우리는 클래스 불균형을 다루기 위한 이전 접근에 비해 더 효율적인 대안으로 새로운 loss 함수를 제안한다. loss 함수는 동적으로 scaled인 cross entropy loss로 여기서 scaling factor는 올바른 클래스에 대한 confidence가 증가함에 따라 0으로 감소한다. 그림 1 참조. 직관적으로 이 scaling factor는 학습하는 동안 쉬운 예제의 기여를 자동적으로 낮추고 모델이 빠르게 어려운 예제에 집중할 수 있게 한다. 실험 결과 우리가 제안한 Focal Loss를 통해 높은 정확도의 one-stage detector를 학습할 수 있으며, 이는 샘플링 휴리스틱이나 hard example mining 같은 one-stage detector를 학습하기 위한 이전 최첨단 기법을 사용하는 대안을 크게 능가한다. 마지막으로 우리는 focal loss의 정확한 형식이 중요하지 않음에 주목하며, 다른 구현 방식으로도 유사한 결과를 달성할 수 있음을 보인다.
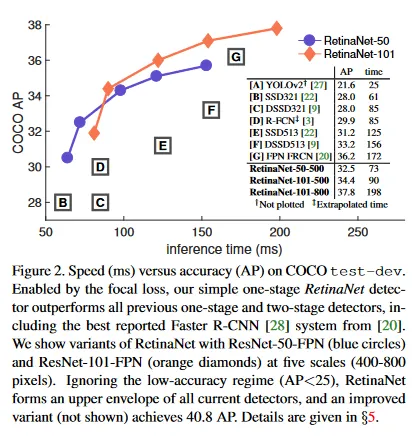
제안된 focal loss의 효과를 보이기 위해 우리는 RetinaNet이라 부르는 간단한 one-stage object detector를 설계한다. 이 이름은 입력 이미지에서 object location를 dense sampling하는 것에서 유래했다. 이것의 설계는 효율적인 네트워크 내 feature pyramid와 앵커 박스를 사용을 특징으로 한다. 이는 [22, 6, 28, 20]의 다양한 최근 아이디어를 활용한다. RetinaNet은 효율적이고 정확하다. ResNet-101-FPN backbone에 기반한 우리의 최고 모델은 5fps로 실행되면서 39.1의 COCO test-dev AP을 달성하여 one-stage와 two-stage detector 모두에서 이전의 공개된 최고의 단일 모델 결과를 능가한다. 그림 2 참조.
2. Related Work
Classic Object Detectors
분류기를 dense image grid에 적용하는 sliding window 패러다임은 길고 풍부한 역사를 갖는다. 초기 성공 중의 하나는 손글씨 숫자 인식에 convolutional neural network를 적용한 classic LeCun et al의 작업이다. Viola and Jones는 얼굴 인식에 boosted object detector를 사용하여 이런 모델의 광범위한 적용을 이끌었다. HOG와 integral channel feature의 도입은 보행자 인식을 위한 효과적인 방법을 만들었다. DPM은 dense detector를 더 일반적인 객체 카테고리로 확장하는데 도움을 주었고 수년 간 PASCAL에 최고 결과를 보였다. sliding-window 접근이 classic computer vision에서 leading detection 패러다임이었지만 deep learning의 재기와 함께 다음에 설명할 two-stage detectors가 빠르게 object detection을 지배하게 되었다.
Two-stage Detectors
최근 object detection를 지배하는 패러다임은 two-stage 접근에 기반한다. Selective Search 작업에서 선구적으로 제시된 바와 같이, 첫 번째 단계에서는 대부분의 negative location를 필터링하면서 모든 객체를 포함해야 하는 후보 proposal의 희소 집합을 생성하고, 두 번째 단계에서 이 proposal을 foreground classes/background로 분류한다. R-CNN은 두번째 단계 분류기를 convolutional networok로 업그레이드하여 정확도를 크게 향상시키고 현대 object detection의 시대를 열었다. R-CNN은 속도 면에서 그리고 학습된 object proposal을 사용함으로써 수년에 걸쳐 개선되었다. Region Proposal Network(RPN)은 proposal 생성을 두 번째 단계 분류기와 단일 convolution network로 통합하여 Faster R-CNN 프레임워크를 형성했다. 이 프레임워크에 대해 수많은 확장이 제안되었다.
One-stage Detectors
OverFeat은 신경망에 기반한 첫 번째 one-stage object detector 중 하나였다. 최근에는 SSD와 YOLO는 one-stage 방법에 대한 관심을 다시 끌었다. 이러한 detector들은 속도에 최적화되었지만 정확도는 two-stage 방법을 뒤쳐졌다. SSD는 10-20% 더 낮은 AP인 반면 YOLO는 더 극단적인 속도/정확도 tradeoff에 초점을 맞추었다. 그림 2 참조. 최근 연구는 two-stage detector가 입력 이미지 해상도와 proposal의 수를 줄이는 것만으로도 간단하게 빠르게 만들 수 있음을 보였지만 one-stage 방법은 더 큰 계산 예산을 사용해도 정확도에서 뒤쳐졌다. 반면 본 작업의 초점은 one-stage detector가 two-stage detector의 정확도와 일치 또는 능가하면서 유사한 더 빠른 속도를 실행할 수 있는지 이해하는 것이다.
우리의 RetinaNet detector의 설계는 이전의 dense detector와 많은 유사성을 공유한다. 특히 RPN에 의해 도입된 ‘anchor’의 개념과 SSD와 FPN에서 사용된 features pyramids가 그렇다. 우리는 우리의 간단한 detector가 네트워크 설계의 혁신에 기반하지 않고 새로운 loss 때문에 최상위 결과를 달성한다는 점을 강조한다.
Class Imbalance
boosted detector나 DPM 같은 classic one-stage object detection 방법과 SSD 같은 더 최근 방법들은 학습하는 동안 큰 클래스 불균형을 직면한다. 이러한 detector들은 이미지당 -개의 후보 location을 평가하지만 극소수의 location만 object를 포함한다. 이러한 불균형은 두 가지 문제의 원인이다. (1) 대부분 location이 유용한 학습 신호를 제공하지 않는 쉬운 negative이기 때문에 학습이 비효율적이다. (2) 대량의 쉬운 negative가 학습을 압도하여 모델을 퇴화시킨다. 일반적인 해결책은 학습하는 동안 hard example을 샘플하는 hard negative mining이나 더 복잡한 sampling/reweighting scheme를 수행하는 것이다.
반면 우리가 제안한 focal loss는 one-stage detector가 직면하는 클래스 불균형을 자연스럽게 다루고 샘플링 없이 그리고 쉬운 negative들이 loss와 계산된 gradient를 압도하지 않으면서 모든 예제에 대해 효율적인 학습을 허용한다.
Robust Estimation
큰 에러를 가진 예제(hard 예제)의 loss를 줄여서 outlier의 기여를 줄이는 견고한 loss 함수(예: Huber loss)를 설계하는 것에 많은 관심이 있었다. 반면 우리의 focal loss는 outlier를 다루는 대신 클래스 불균형을 해결하도록 설계되었다. 이는 inlier를 가중치를 낮춤으로써, 그들의 수가 많더라도 total loss에 대한 기여가 작도록 한다. 다시 말해 focal loss는 robust loss의 반대 역할을 수행한다. 이것은 희소한 hard 예제의 집합을 학습하는 것에 초점을 맞춘다.
3. Focal Loss
Focal Loss는 학습하는 동안 foreground와 background class 사이에 극단적인 불균형(예: 1:1000)이 존재하는 one-stage object detection 시나리오를 해결하기 위해 설계되었다. 우리는 binary classification를 위한 cross entropy(CE)에서 시작하여 focal loss를 소개한다.
위에서 은 ground-truth class를 지정하고 은 라벨 인 클래스에 대한 모델의 추정 확률이다. 표기의 간편함을 위해 를 정의한다.
그리고 로 재작성한다.
CE loss는 그림 1에서 파란 (상단) 커브로 볼 수 있다. 이 손실의 주목할만한 속성은 그래프에서 쉽게 볼 수 있듯이, 쉽게 분류되는 예제들() 조차 무시할 수 없는 크기의 손실을 발생시킬 수 있다는 것이다. 많은 수의 쉬운 예제에 대해 이러한 작은 손실 값을 합산할 때, 희소한 클래스를 압도할 수도 있다.
3.1. Balanced Cross Entropy
클래스 불균형을 해결하기 위한 일반적인 방법은 class 에 대해 가중치 과 class 에 대해 를 도입하는 것이다. 실제로 는 클래스 빈도의 역수로 설정하거나 cross validation에 의해 설정할 하이퍼파라미터로 취급될 수 있다. 표기의 간편함을 위해 를 정의한 것과 유사하게 를 정의한다. -balanced CE loss를 다음과 같이 정의한다.
이 loss는 CE에 대한 간단한 확장으로 우리가 제안하는 focal loss에 대한 실험적 baseline으로 고려한다.
3.2. Focal Loss Definition
우리의 실험이 보이는 것처럼 dense detector를 학습하는 동안 마주치는 큰 클래스 불균형은 cross entropy loss를 압도할 수 있다. 쉽게 분류되는 negative 샘플들이 log의 대부분을 차지하고 gradient를 지배한다. 가 positive/negative 예제의 중요성을 균형 잡지만, easy/hard 예제를 구별하지 않는다. 대신 loss 함수를 재구성하여 easy 예제의 가중치를 낮추고, hard negative를 학습하는데 초점을 맞추는 것을 제안한다.
더 형식적으로 우리는 cross entropy loss에 조정 가능한 focusing 파라미터 을 갖는 modulating factor 를 추가할 것을 제안한다. 우리는 focal loss를 다음과 같이 정의한다.
focal loss는 그림 1에서 의 여러 값에 대해 시각화 된다. 우리는 focal loss의 2가지 속성을 주목한다. (1) 예제가 misclassified이고 가 작을 때, modulating factor는 에 가까워지고 loss에는 영향이 없다. 로 감에 따라 factor는 으로 가고 well-classified 예제에 대한 loss는 down-weighted된다. (2) focusing 파라미터 는 쉬운 예제의 가중치가 낮아지는 속도를 완만하게 조정한다. 일 때, FL은 CE와 동일하고 가 증가함에 따라 modulating factor의 효과도 마찬가지로 증가된다(우리 실험에서 일 때 best 임을 발견했다)
직관적으로 modulating factor는 쉬운 예제의 loss 기여를 줄이고 낮은 loss를 받는 예제의 범위를 확장한다. 예컨대 일 때 로 분류되는 예제는 CE와 비교하여 100배 낮은 loss를 갖고 이면 CE와 비교하여 1000배 낮은 loss를 갖는다. 이것은 결과적으로 misclassified 예제를 조정하는 것의 중요성을 증가시킨다.(이고 일 때 loss는 최대 4배까지만 축소된다.)
실제로 focal loss의 -balanced 변종을 사용했다.
우리의 실험에서 이 형태를 채택했는데, 이것이 비 -balanced 형식에 대해 약간 개선된 정확도를 산출하기 때문이다. 마지막으로 loss 레이어의 구현에서 를 계산하기 위한 sigmoid 연산과 loss 계산을 결합하여 더 큰 수치적 안정성을 얻었음을 언급한다.
우리의 주요 실험 결과에서 위에 정의된 focal loss를 사용하지만, 그 정확한 형식은 핵심적이지 않다. 부록에서 focal loss의 다른 인스턴스를 고려하고 그것들이 동등한 효과를 가짐을 보인다.
3.3. Class Imbalance and Model Initialization
binary classification 모델은 기본적으로 또는 을 출력하는 확률을 동등하게 초기화한다. 이런 초기화 아래 클래스 불균형이 존재할 경우, 빈번한 클래스로 인한 loss가 전체 loss를 지배할 수 있고, 초기 학습에서 불안정성의 원인이 될 수 있다. 이것을 해결하기 위해 우리는 학습의 시작에서 희소 클래스(foreground)에 대해 모델이 추정한 값에 대한 ‘prior’의 개념을 도입한다. 우리는 prior를 로 표기하고, 희소 클래스의 예제에 대한 모델의 추정 값이 낮도록(예: 0.01) 설정한다. 우리는 loss 함수의 변경이 아닌 모델 초기화에서 변경임에 주목해야 한다. 우리는 이것이 심각한 클래스 불균형 경우에서 cross entropy와 focal loss 모두에 대해 학습 안정성을 증가시키는 것을 발겼했다.
3.4. Class Imbalance and Two-stage Detectors
Two-stage detectors는 종종 -balancing 또는 우리가 제안한 loss를 사용하지 않고 cross entropy loss로 학습된다. 대신 그들은 2가지 메커니즘으로 클래스 불균형을 해결한다. (1) two-stage cascade (2) biased mini-batch sampling. 우선 cascade stage는 object proposal 메커니즘으로 거의 무한한 객체 위치의 집합을 1000-2000개로 줄인다. 중요한 점은 selected proposal이 무작위가 아니라 실제 객체 위치에 해당할 가능성이 높아 대부분의 easy negative을 제거한다는 것이다. 2번째 stage를 학습할 때, 일반적으로 biased sampling이 사용되어 예컨대 positive 대 negative 예제의 비율이 1:3인 미니배치를 구성한다. 이 비율은 샘플링을 통해 구현되는 암시적 -balancing factor와 유사하다. 우리가 제안하는 focal loss는 one-stage detection 시스템에서 이러한 메커니즘을 loss 함수를 통해 직접적으로 다루도록 설계되었다.
4. RetinaNet Detector
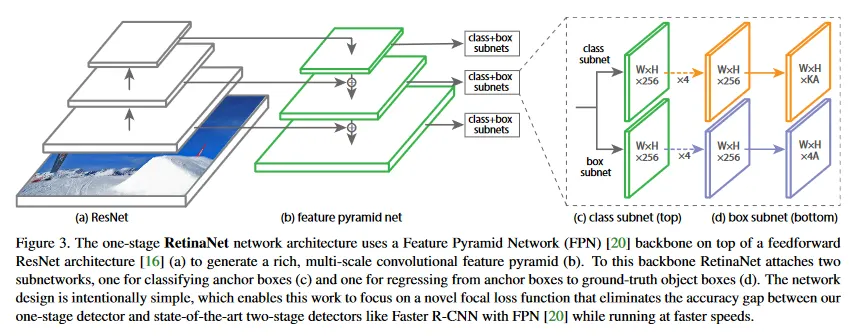
RetinaNet은 backbone network와 2개의 작업 특화된 subnetwork로 구성된 단일, 통합된 네트워크이다. backbone은 전체 입력 이미지에 대해 convolutional feature map을 계산하기 위한 역할을 하고 off-the-self(기성품) convolutional network이다. 첫 번째 subnet은 backbone의 출력에 대해 convolutional object classification을 수행하고, 두 번째 subnet은 convolutional bounding box regression을 수행한다. 두 subnetwork는 우리가 특별히 one-stage, dense detection를 위해 제안하는 간단한 설계를 특징으로 한다(그림 3 참조). 이러한 구성 요소의 세부사항에 대해 많은 가능한 선택이 있지만, 실험 결과에서 보이듯이 대부분 설계 파라미터는 정확한 값에 특별히 예민한지 않다. 다음으로 RetinaNet의 각 구성 요소를 설명한다.
Feature Pyramid Network Backbone
우리는 RetinaNet을 위한 backbone 네트워크로 Feature Pyramid Network(FPN)을 채택했다. 간략히 설명하면 FPN은 표준 convolutional 네트워크에 top-down pathway와 lateral connection을 추가하여 네트워크가 단일 해상도 입력 이미지에서 풍부한 multi-scale feature 피라미드를 효율적으로 구성할 수 있게 한다. 그림 3(a)-(b) 참조. 피라미드의 각 레벨은 다양한 스케일에서 객체를 검출하는데 사용될 수 있다. FPN은 fully convoutional network(FCN)에서 multi-scale 예측을 개선한다. 이는 RPN과 DeepMask-style proposal, 그리고 Fast R-CNN이나 Mask R-CNN과 같은 two-stage detector 에서의 성능 향상을 통해 입증되었다.
[20]을 따라 우리는 ResNet 아키텍쳐의 위에 FPN을 구축한다. 우리는 에서 까지의 레벨로 피라미드를 구축한다. 여기서 은 피라미드 레벨을 나타낸다(은 입력 보다 배 낮은 해상도를 갖는다) [20]과 같이 모든 피라미드 레벨은 채널을 갖는다. 피라미드의 상세는 일반적으로 [20]을 따르지만 몇 가지 작은 차이가 있다. 많은 설계 선택은 핵심적이지 않지만 우리는 FPN backbone의 사용을 강조한다. 이것은 최종 ResNet 레이어의 feature만 사용한 preliminary 실험에서 낮은 AP를 산출했다.
Anchors
우리는 [20]의 RPN 변종과 유사한 translation-invariant 앵커 박스를 사용한다. 앵커는 피라미드 레벨 에서 까지에 대해 각각 에서 의 영역을 갖는다. [20]에서와 같이 각 피라미드 레벨에서 우리는 의 3가지를 가진 앵커를 사용한다. [20]보다 더 밀집한 scale 커버리지를 위해, 각 레벨에서 원래의 3가지 종횡비 앵커의 집합에 의 크기의 앵커를 추가한다. 이것은 우리의 설정에서 AP를 개선했다. 총 레벨당 개의 앵커가 존재하고 레벨에 전체에 걸쳐 네트워크 입력 이미지에 대해 32-813 픽셀 스케일 범위를 커버한다. .
각 앵커에는 길이 의 원-핫 벡터 분류 타겟(는 객체 클래스의 수)과 4-벡터의 박스 regression 타겟이 할당된다. 우리는 RPN의 할당 규칙을 사용하지만 multi-class 검출를 위해 수정하고 threshold를 조정했다. 구체적으로 앵커는 0.5의 intersection-over-union(IoU) threahold를 사용하여 ground-truth 객체 박스에 할당되고, IoU가 내에 존재하면 background로 할당된다. 각 앵커는 최대 하나의 객체 박스에 할당되므로, 해당 길이 라벨 벡터의 해당 항목을 로 설정하고 다른 모든 항목을 으로 설정한다. 앵커가 할당되지 않은 경우 에서 중첩될 수 있고 학습하는 동안 무시된다. 박스 regression 타겟은 각 앵커와 할당된 객체 박스 사이의 offset으로 계산되며, 할당이 없으면 생략된다.
Classification Subnet
classfication subnet은 개 앵커와 개 객체 클래스의 각각에 대해 각 공간 위치에서 객체가 존재할 확률을 예측한다. 이 subnet은 각 FPN 레벨에 추가된 작은 FCN이다. 이 subnet의 파라미터는 모든 피라미드 레벨에서 공유된다. 이 설계는 간단하다. 주어진 피라미드 레벨에서 개 채널을 가진 입력 feature map을 취하고, subnet은 각 개 필터를 가진 4개의 3x3 conv layer를 적용하고 레이어 뒤에는 각 ReLU 활성화가 따른다. 그 다음 개 필터를 가진 3x3 conv layer가 이어진다. 마지막으로 sigmoid 활성화가 공간 위치당 개 binary 예측을 출력하도록 추가된다. 그림 3(c) 참조. 우리는 대부분의 실험에서 과 을 사용한다.
RPN과 다르게, 우리의 object classification subnet은 더 깊고, 3x3 conv만 사용하며, 박스 regression subnet(이후에 설명할)과 파라미터를 공유하지 않는다. 우리는 이러한 higher-level 설계 결정이 하이퍼파라미터의 특정한 값보다 더 중요함을 발견했다.
Box Regression Subnet
object classification subnet과 병렬로, 우리는 각 피라미드 레벨에 또 다른 작은 FCN을 추가한다. 이것은 각 앵커 박스에서 근처의 ground-truth 객체(존재하는 경우)까지와의 offset을 회귀하기 위한 목적이다. 박스 회귀 subnet의 설계는 classification subnet과 동등하지만, 공간 위치당 개 선형 출력으로 끝난다는 점이 다르다. 그림 3(d) 참조. 공간 위치당 개 앵커의 각각에 대해 이러한 개 출력은 앵커와 ground-truth box 사이의 상대적 offset을 예측한다. (우리는 R-CNN의 표준 박스 파라미터화를 사용한다) 대부분의 최근 연구와 다르게, 우리는 class-agnostic bounding box regressor를 사용하는데, 이것은 더 적은 파라미터를 사용하면서도 동등하게 효과적임을 발견했다. object classification subnet과 box regression subnet은 공통의 구조를 공유하지만, 별도의 파라미터를 사용한다.
4.1. Inference and Training
Inference
RetinaNet은 ResNet-FPN backbone, classification subnet과 box regression subnet으로 구성된 단일 FCN을 형성한다. 그림 3 참조. 추론은 단순히 이미지를 네트워크를 통해 forwarding하는 것을 포함한다. 속도를 개선하기 위해 우리는 detector confidence를 에서 thresholding한 후에 FPN 레벨 당 최대 1K개의 최고 점수 예측에서만 박스 예측을 디코딩한다. 모든 레벨에서 상위 예측들은 병합되고, 의 threshold로 non-maximum suppression가 적용되어 최종 탐지를 산출한다.
Focal Loss
이 연구에서 도입된 focal loss를 classification subnet의 출력에 대한 loss로 사용한다. 섹션 5에서 보이는 바와 같이 우리는 가 실제에서 잘 작동하고 RetinaNet은 에서 상대적으로 견고함을 발견했다. RetinaNet을 학습할 때, focal loss가 샘플된 각 이미지의 모든 ~100k 앵커에 적용된다는 점을 강조한다. 이것은 각 미니배치를 대해 작은 앵커 집합(예 256)을 선택하기 위해 휴리스틱 샘플링(RPN) 또는 hard example mining(OHEM, SSD)를 사용하는 일반적인 관행과 대조된다. 이미지의 총 focal loss는 ~100k 앵커에 대한 focal loss의 합산으로 계산되며, ground-truth 박스에 할당된 앵커의 수로 normalized한다. 우리는 총 앵커 수가 아니라 할당된 앵커의 수에 의해 normalization을 수행한다. 대부분의 앵커가 쉬운 negative이고 focal loss에서 무시할 수 있는 loss 값을 받기 때문이다. 마지막으로 우리는 희소 클래스에 할당된 가중치인 도 안정적인 범위를 가지지만 와 상호작용하여 두 값을 함께 선택해야 함을 강조한다(표 1a와 1b 참조). 일반적으로 가 증가함에 따라 를 약간 감소시켜야 한다. (가 가장 잘 작동했다.)
Initialization
우리는 ResNet-50-FPN과 ResNet-101-FPN을 backbone으로 사용하여 실험한다. 기본 ResNet-50과 ResNet-101 모델은 ImageNet 1k에 대해 pre-trained이고 우리는 [16]에 의해 공개된 모델을 사용한다. FPN을 위해 추가된 새로운 레이어들은 [20]에서와 같이 초기화된다. RetinaNet subnet에서 마지막 하나만 제외하고 모든 new conv layer는 bias 와 인 가우시안 가중치 채우기로 초기화된다. classification subnet의 최종 conv layer의 경우, bias 초기화를 로 설정한다. 여기서 는 학습 시작시 모든 앵커가 ~의 confidence로 foreground로 라벨링되어야 한다는 것을 지정한다. 우리는 모든 실험에서 을 사용하지만 결과는 exact value에 대해 견고하다. 섹션 3.3에서 설명한대로, 이 초기화는 많은 수의 background 앵커가 학습의 첫 iteration에서 큰 불안정한 손실 값을 생성하는 것을 방지한다.
Optimization
RetinaNet은 stochastic gradient descent(SGD)로 학습된다. 우리는 8개 GPU에 대해 동기화된 SGD를 사용하며, 미니배치당 총 16개의 이미지(GPU당 2개 이미지)를 사용한다. 달리 명시하지 않는 한(unless otherwise specified), 모든 모델은 90k iteration으로 학습되며, 초기 learning rate을 에서 시작하여 60k 반복에서 10으로 나누고, 다시 80k 반복에서 10으로 나눈다. 달리 언급하지 않는 한(unless otherwise noted), 우리는 horizontal image flipping을 유일한 데이터 증강의 형식으로 사용한다. 0.0001의 weight decay와 0.9의 momentum을 사용한다. 학습 손실은 focal loss와 박스 회귀를 위한 표준 smooth loss의 합을 사용한다. Table 1e의 모델에 대해 학습 시간은 10-35 시간 사이이다.
5. Experiments
우리는 도전적인 COCO 벤치마크의 bounding box detection track에 대한 실험 결과를 제시한다. 학습을 위해, 우리는 일반적인 관행을 따라 COCO trainval35k split(train에서 80k 이미지와 40k 이미지 val 분할에서 무작위로 선택된 35k 이미지 부분집합의 합집합)을 사용한다. 우리는 minival split(val에서 남은 5k 이미지)에 대한 평가를 통해 장애와 민감성 연구를 리포트한다. 우리의 주요 결과에 대해 공개된 라벨이 없고 평가 서버 사용이 필요한 test-dev split에 대한 COCO AP를 리포트한다.
5.1. Training Dense Detection
우리는 dense detection을 위한 loss 함수의 동작과 다양한 최적화 전략을 따라 분석하기 위해 수많은 실험을 실행한다. 모든 실험에서 우리는 상단에 Feature Pyramid Network(FPN)가 구축된 depth 50 또는 101 ResNet을 사용한다. 모든 ablation 연구를 위해 우리는 학습과 테스트를 위해 600 픽셀의 이미지 스케일을 사용한다.
Network Initialization
RetinaNet을 학습시키기 위한 우리의 첫 시도는 초기화나 학습 전략에 대한 어떤 수정 없이 표준 cross entropy(CE) loss를 사용한다. 이것은 빠르게 실패하며 학습하는 동안 네트워크가 발산한다. 그러나 단순히 모델의 마지막 레이어를 object detecting의 prior 확률이 이 되도록 초기화하는 것만으로도(섹션 4.1) 효율적인 학습을 할 수 있다. ResNet-50과 이 초기화를 사용하여 RetinaNet을 학습하면 이미 COCO에서 의 AP를 산출한다. 결과는 의 정확한 값에 민감하지 않기 때문에 우리는 모든 실험에서 을 사용한다.
Balanced Cross Entropy
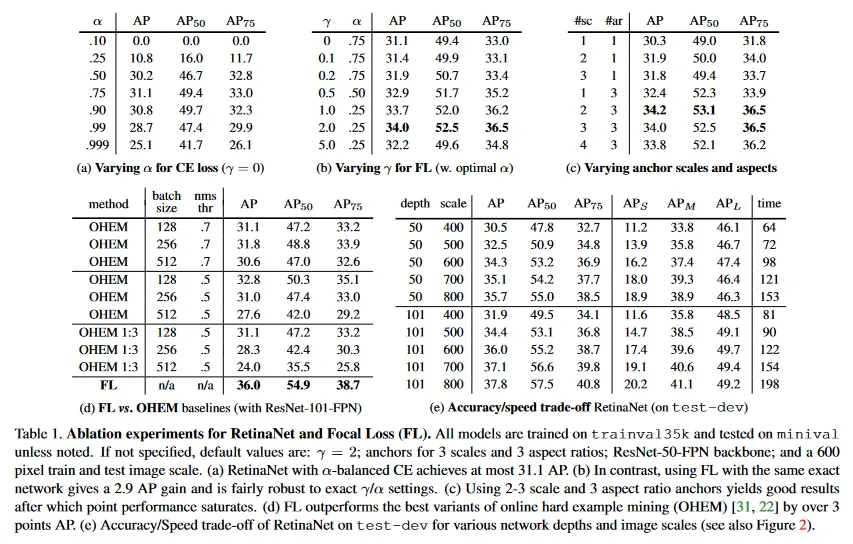
학습을 개선하기 위한 우리의 다음 시도는 섹션 3.1에서 논의한 -balanced CE loss를 사용하는 것이다. 의 다양한 값에 대한 결과는 Table 1a에서 보여진다. 를 설정하면 AP 점수가 점 상승한다.
Focal Loss
우리가 제안한 focal loss를 사용하는 결과는 Table 1b에서 보여진다. focal loss는 modulating 항의 강도를 제어하는 focusing 파라미터 라는 새로운 하이퍼파라미터를 도입한다. 일 때 우리의 loss는 CE loss와 동등하다. 를 증가시킴에 따라 loss 형태가 변화하여 낮은 loss를 갖는 easy 예제들이 추가로 discount 된다. 그림 1 참조. FL은 가 증가함에 따라 CE에 대해 큰 이점을 얻는다. 일 때, FL은 -balanced CE loss에 대해 AP 개선을 산출한다.
Table 1b의 실험 결과에서 공정한 비교를 위해 각 에 대한 최적의 를 찾는다. 우리는 더 높은 에 대해 더 낮은 가 선택된다는 것을 관찰한다(easy negative의 가중치가 낮아짐에 따라 positive에 대한 강조가 덜 필요해진다) 그러나 전체적으로 을 변경하는 이점이 훨씬 더 크고, 실제로 최적의 의 범위는 에 불과했다(우리는 를 테스트했다). 우리는 모든 실험에서 의 을 사용한다. 그러나 는 근접하게 잘 작동한다(점 낮은 AP)
Analysis of the Focal Loss
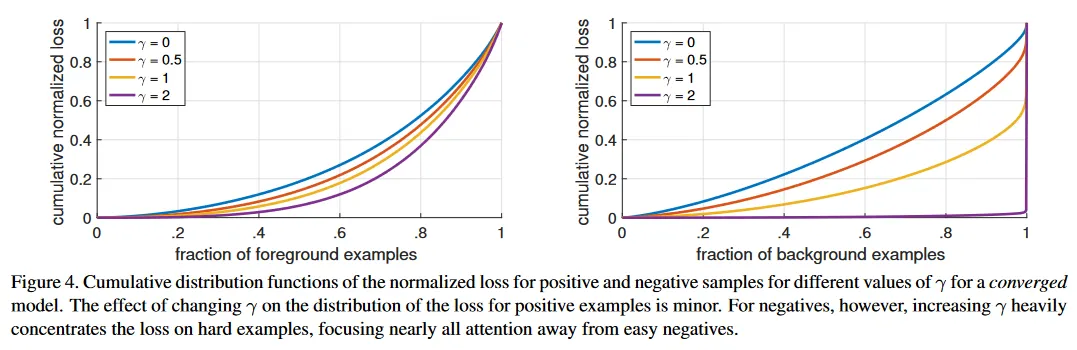
focal loss를 더 잘 이해하기 위해 우리는 수렴된 모델의 loss의 실험적 분포를 분석한다. 이를 위해 우리는 로 학습된 default ResNet-101 600픽셀 모델을 사용한다(이것은 점의 AP). 이 모델을 다수의 무작위 이미지에 적용하고 ~ negative windows와 ~ positive windows에 대한 예측 확률을 샘플링한다. 다음으로 positive와 negative에 대해 별도로 이 샘플들에 대한 FL을 계산하고 loss를 합해서 1이 되도록 normalize 한다. normalize loss가 주어지면 우리는 가장 낮은 것에서 가장 높은 것까지 loss를 정렬할 수 있고, positive와 negative 샘플에 대해 그리고 다양한 설정에 대해 cumulative distribution function(CDF)로 plot 할 수 있다(모델이 로 학습되었음에도).
positive와 negative 샘플에 대한 CDF는 그림 4에 보여진다. positive 샘플을 관찰하면 CDF가 의 다양한 값에 대해 상당히 유사해 보이는 것을 볼 수 있다. 예컨대 가장 어려운 positive 샘플의 약 20%가 positive loss의 대략 절반을 차지하며 가 증가함에 따라 더 많은 loss가 상위 20%의 예제에 집중되지만 그 효과는 작다.
negative 샘플에 대한 의 효과는 드라마틱하게 다르다. 의 경우 positive와 negative CDF는 매우 유사하다. 그러나 를 증가시킴에 따라 상당히 더 많은 가중치가 hard negative 예제에 집중된다. 실제로 (우리의 기본 설정)에서 loss의 대부분은 작은 비율의 샘플에서 발생한다. 보이는대로 FL은 easy negative의 효과를 효율적으로 감소시키고, 모든 주의를 hard negative 예제에 집중시킨다.
Online Hard Example Mining (OHEM)
[31]은 high-loss 예제를 사용하여 minibatch를 구축함으로써 two-stage detector의 학습을 개선하도록 제안했다. 구체적으로 OHEM에서 각 예제가 loss에 의해 점수 매겨지고, non-maximum suppression(nms)가 적용된 후, 가장 높은 loss 예제들로 미니배치가 구성된다. nms threshold와 batch 크기는 조정가능한 파라미터이다. focal loss와 유사하게 OHEM은 잘못 분류된 예제에 대해 더 많은 강조를 두지만, FL과 달리 OHEM은 easy 예제를 완전히 폐기한다. 우리는 또한 SSD에서 사용된 OHEM의 변종을 구현한다. 모든 예제에 nms를 적용한 후에, 미니배치는 각 미니배치가 충분한 positive를 보장하기 위해 positive와 negative 사이에 1:3 비율을 강제하도록 구성된다.
우리는 큰 클래스 불균형을 가진 one-stage detection의 설정에서 두 OHEM의 변종을 모두 테스트 한다. 선택된 배치 크기와 nms threshold에 대한 원래의 OHEM 전략과 OHEM 1:3 전략의 결과는 Table 1d에 보여진다. 이 결과는 ResNet-101을 사용하고, FL을 사용하여 학습된 우리의 baseline은 이 설정에서 AP를 달성했다. 대조적으로 OHEM에 대한 최적의 설정(1:3 비율 없이, 배치 크기 128, 0.5의 nms)는 AP를 달성했다. 이것의 격차는 AP로 FL이 dense detector를 학습에 대해 OHEM 보다 더 효율적임을 보인다. 우리는 OHEM에 대해 다른 파라미터 설정과 변종을 시도했지만 더 나은 결과를 달성하지 못했음을 언급한다.
Hinge Loss
마지막으로 초기 실험에서 우리는 에 대한 hinge loss를 사용하여 학습을 시도했다. 이것은 의 특정한 값 이상에서 loss를 으로 설정한다. 그러나 이것은 불안정하고 의미있는 결과를 얻지 못했다. 대체 loss 함수를 탐색한 결과는 부록 참조.
5.2. Model Architecture Design
Anchor Density
one-state detection system에서 가장 중요한 설계 요인 중 하나는 가능한 이미지 박스의 공간을 얼마나 밀집으로 커버하느냐이다. two-stage detector는 region pooling 연산을 사용하여 임의의 position, scale, 종횡비의 박스도 분류할 수 있다. 반면에 one-stage detector는 고정된 샘플링 grid를 사용하므로, 이러한 접근에서 박스의 높은 범위를 달성하기 위한 대중적인 접근은 각 공간 position에서 다양한 스케일과 종횡비의 박스를 커버하기 위해 multiple anchor를 사용하는 것이다.
우리는 FPN의 각 공간 position과 각 피라미드 레벨에서 사용되는 scale과 종횡비 앵커의 수를 조사했다. 우리는 각 location에서 단일 정사각 앵커에서 4개의 sub-octave scale(에 대해 )과 3가지 종횡비 를 포괄하는 location 당 12개 앵커까지의 경우를 고려한다. ResNet-50을 사용한 결과는 Table 1c에서 보여진다. 하나의 정사각 앵커만 사용해도 놀랍게도 좋은 AP()가 달성될 수 있다. 그러나 location 당 3가지 scale과 3가지 종횡비를 사용하면 AP를 거의 4점(까지) 개선할 수 있다. 우리는 이러한 설정을 이 연구의 다른 모든 실험에서 사용한다.
마지막으로 우리는 6-9개 앵커 너머 증가시켜도 추가적인 이득이 없음을 주목한다. 따라서 two-stage 시스템이 이미지에서 임의의 박스를 분류할 수 있지만, 밀도에 대한 성능 포화는 two-stage 시스템의 잠재적으로 더 높은 밀도가 이점을 제공하지 않는다는 것을 시사한다.
Speed versus Accuracy
더 큰 backbone 네트워크는 더 높은 정확도를 산출하지만 추론 속도가 더 느려진다. 입력 이미지 크기에 대해서도 유사하다(더 짧은 이미지 면에 의해 정의됨). 우리는 이 두가지 요인의 영향을 Table 1e에서 보인다. 그림 2에서 우리는 RetinaNet에 대해 속도/성능 trade-off curve를 plot하고 COCO test-dev에 대한 최근 방법들의 공개된 수치와 비교한다. 이 plot은 우리의 focal loss으로 가능해진 RetinaNet이 낮은 정확도 영역을 제외하고 모든 기존 방법들의 상위 경계를 형성함을 보인다.
ResNet-101-FPN과 600 픽셀 이미지 scale을 사용하는 RetinaNet(단순성을 위해 RetinaNet 101-600라고 표기)는 최근에 공개된 ResNet-101-FPN Faster R-CNN의 정확도와 일치하면서, 이미지 당 172ms와 대비하여 122ms에서 실행된다(둘 다 Nvidia M40 GPU에서 측정됨). 더 큰 스케일을 사용하면 RetinaNet은 여전히 더 빠르면서도 모든 two-stage 접근의 정확도를 능가한다. 더 빠른 실행시간을 위해 ResNet-50-FPN을 사용하는 것이 ResNet-101-FPN에 대해 개선하는 작동 지점은 단 하나(500 픽셀 입력) 뿐이다. 높은 frame 속도를 다루려면 [27]에서와 같이 특별한 네트워크 설계를 요구된다. 이것은 이 연구의 범위를 벗어난다. 우리는 공개 후에 [12]의 Faster R-CNN의 변종을 통해 더 빠르고 더 정확한 결과를 얻을 수 있었음을 언급한다.
5.3. Comparison to State of the Art
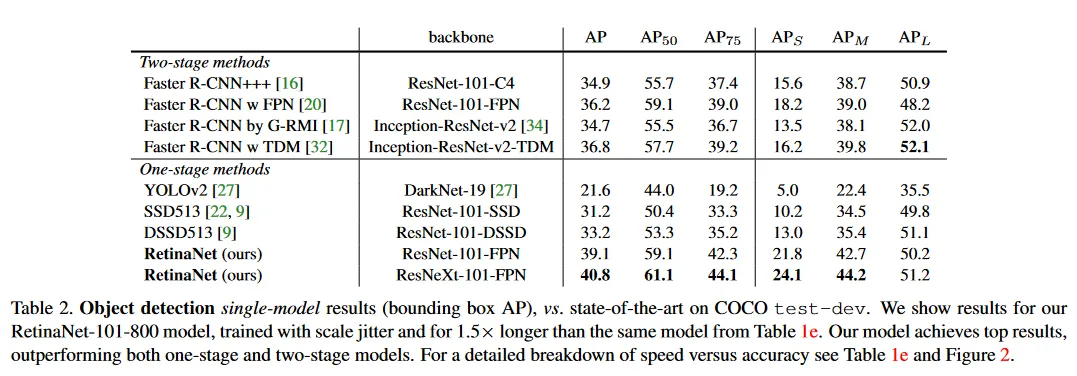
우리는 도전적인 COCO 데이터셋에서 RetinaNet을 평가하고, one-stage와 two-stage 모델 모두를 포함하여 최첨단 성능의 방법들과 test-dev 결과를 비교한다. 결과는 Table 2에 나타난다. scale jitter를 사용하고 Table 1e의 모델 보다 1.5배 더 길게 학습된 RetinaNet-101-800 모델에 대한 것이다( AP 이득 제공). 기존 one-stage 방법과 비교하여 우리의 접근은 가장 근접한 경쟁자인 DSSD에 대해 상당한 점 AP 격차( vs )를 달성하면서도 더 빠르다. 그림 2 참조. 최근의 two-stage 방법과 비교하여 RetinaNet은 Inception-ResNet-v2-TDM에 기반한 최고 성능의 Faster R-CNN 모델 보다 점 높은 격차를 달성한다. RetinaNet backbone으로 ResNeXt-32x9d-101-FPN을 연결하면 추가로 AP를 개선하여 COCO에서 AP를 넘어선다.
6. Conclusion
이 연구에서 우리는 클래스 불균형을 one-stage detector가 최고 성능의 two-stage 방법을 능가하지 못하게 하는 주요한 방해물로 식별했다. 이것을 해결 하기 위해 우리는 focal loss를 제안한다. 이것은 cross entropy에 수정항을 추가하여 학습을 hard negative 예제에 집중시킨다. 우리의 접근은 간단하고 매우 효과적이다. 우리는 fully convolutional one-stage detector를 설계하여 그 효과를 집증하고, 광범위한 실험 분석을 통해 최첨단 정확도와 속도를 달성함을 리포트한다. 소스코드는 참조.
Appendix A: Focal Loss*
focal loss의 정확한 형식은 중요하지 않다. 우리는 이제 유사한 속성을 가지고 비슷한 결과를 산출하는 focal loss의 대체 인스턴스를 보인다. 다음은 또한 focal loss의 속성에 더 많은 통찰을 제공한다.
우리는 본문에서와 약간 다양한 형식으로 cross entropy(CE)와 focal loss(FL)를 모두 고려하는 것으로 시작한다. 구체적으로 라는 양을 다음과 같이 정의한다.
여기서 은 이전과 같이 ground-truth class를 지정한다. 그러면 로 작성할 수 있다. (이것은 방정식 2의 의 정의와 호환된다.) 예제는 일 때 올바르게 분류되며, 이 경우 이다.
이제 의 측면에서 focal loss의 대체 형식을 정의할 수 있다. 우리는 와 를 다음과 같이 정의한다.
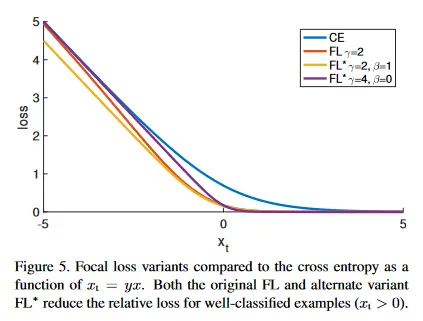
은 loss 커브의 steepness(기울기)와 shift(이동)를 제어하는 2개의 파라미터 와 를 갖는다. 우리는 그림 5에서 선택된 2가지 와 설정에 대한 을 와 옆에 그린다. 볼 수 있는 대로 과 유사하게 선택된 파라미터를 갖는 은 잘 분류된 예제에 할당된 loss를 감소시킨다.
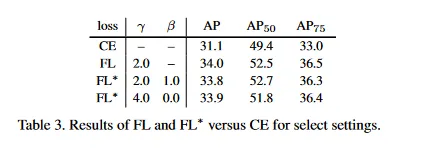
우리는 이전과 같은 동등한 설정을 사용하여 RetinaNet-50-600을 학습시켰지만 대신 선택된 파라미터를 갖는 로 교체했다. 이 모델은 로 학습된 것과 거의 동일한 AP를 달성했다. Table 3 참조. 즉 은 실제에서 잘 작동하는 의 합리적인 대안이다.
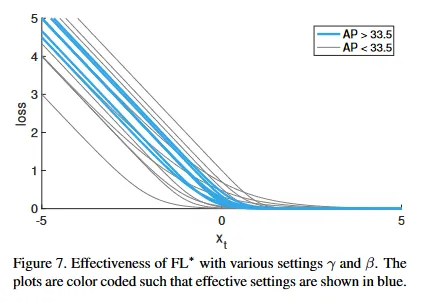
우리는 다양한 와 설정이 좋은 결과를 제공함을 발견했다. 그림 7에서 우리는 광범위한 파라미터의 집합에 대해 을 사용한 RetinaNet-50-600에 대한 결과를 보인다. loss plot은 색상으로 코딩되어 있고 효과적인 설정(모델은 수렴하고 33.5 이상의 AP)은 파란색으로 보여진다. 우리는 단순성을 위해 모든 실험에서 를 사용했다. 볼 수 있는대로 잘 분류된 예제()의 가중치를 줄이는 loss가 효과적이다.
더 일반적으로 우리는 이나 과 유사한 속성을 갖는 임의의 loss 함수가 동등하게 효율적일 것이라 기대한다.
Appendix B: Derivatives
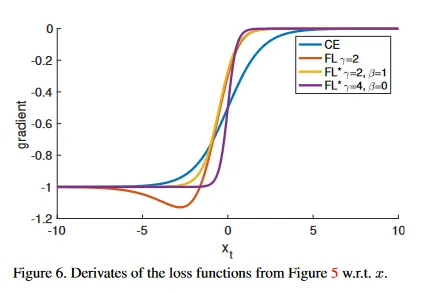
참조를 위해 에 대한 , 과 의 도함수는 다음과 같다.
선택된 설정에 대한 plot은 그림 6에 보여진다. 모든 loss 함수에 대해, 도함수는 high-confidence 예측에 대해 또는 로 수렴한다. 그러나 와 다르게 과 모두의 효과적인 설정에서는 인 경우 도함수가 즉시 작아진다.