Search
Duplicate

AI/ Mamba

State-Space Model(SSM)

State-Space Model(SSM)은 일반적으로 은닉 상태가 관측 변수에 영향을 주는 Markov process를 따르는 모델을 의미하지만, Markov Decision Processes(MDP), Dynamic Causal Modeling(DCM), Kalman Filter, Hidden Markov Models(HMMs), Linear Dynamical System(LDS)과 같이 분야마다 다른 개념으로 사용된다.
Mamba 논문은 제어이론에서의 SSM을 따른다. 이에 대한 상세 내용은 AI/ State Space Model(SSM) 페이지 참조

Structured SSM(S4)

Mamba 논문에서 SSM은 Structured State Space Sequence(S4) Models을 지칭하며, 이 모델은 Structured SSM을 소개한 첫 번째 모델로 다음과 같이 4개 파라미터(Δ,A,B,C)(\Delta, \bold{A}, \bold{B}, \bold{C})를 사용하여 2단계로 seq2seq 변환을 정의하는 모델이다.
h′(t)=Ah(t)+Bx(t)(1a)y(t)=Ch(t)(1b)ht=A‾ht−1+B‾xt(2a)yt=Cht(2b)K‾=(CB‾,CAB‾,...,CA B‾k,...)(3a)y=x∗K‾(3b)\begin{aligned} h'(t) &= \bold{A}h(t) + \bold{B}x(t) & (1a) \\ y(t) &= \bold{C}h(t) &(1b) \\ h_t &= \overline{\bold{A}}h_{t-1} + \overline{\bold{B}}x_t &(2a) \\ y_t &= \bold{C}h_t & (2b) \\ \overline{\bold{K}} &= (\bold{C}\overline{\bold{B}},\bold{C}\overline{\bold{AB}},...,\bold{C}\overset{k}{\overline{\bold{A} \ \bold{B}}}, ... ) & (3a) \\ y &= x * \overline{\bold{K}} & (3b) \end{aligned}
여기서 x(t),h(t),y(t)x(t), h(t), y(t)는 각각 시간 tt에 따라 변하는 입력, 은닉, 출력의 연속 함수이고, xt,ht,ytx_t, h_t, y_t는 각각 시간 tt에서의 입력, 은닉, 출력에 해당하는 이산화된 값이다. 여기서 h′(t)h'(t)는 선형 상미분 방정식(Linear Ordinary Differential Equation, Linear ODE)로 정의되는 h(t)h(t)의 도함수에 해당한다. 이에 대한 정의와 이산화 유도는 AI/ State Space Model(SSM) 페이지 참조.
위 식에서 (2)를 Linear Recurrent라 하고 (3)은 Global Convolution이라 한다.
여기서 A‾,B‾\overline{\bold{A}}, \overline{\bold{B}}는 각각 두 파라미터 A,B\bold{A}, \bold{B}의 이산화된 버전을 의미하며, S4에서는 Zero-Order Hold(ZOH) 규칙이라 부르는 다음의 식을 사용하여 연속 파라미터를 이산화한다.
A‾=exp⁡(ΔA)B‾=(ΔA)−1(exp⁡(ΔA)−I)⋅ΔB(4)\begin{aligned} \overline{\bold{A}} &= \exp(\Delta \bold{A}) \\ \overline{\bold{B}} &= (\Delta \bold{A})^{-1}(\exp(\Delta\bold{A}) -\bold{I})\cdot \Delta \bold{B} \end{aligned} \tag{4}
파라미터를 (Δ,A,B,C)↦(A‾,B‾,C)(\Delta, \bold{A}, \bold{B}, \bold{C}) \mapsto (\overline{\bold{A}},\overline{\bold{B}}, \bold{C})로 변환한 후에 S4 모델은 Linear Recurrent(2)와 Global Convolution(3)를 이용하여 Auto Regressive 추론을 수행한다.
이 모델의 동역학이 시간에 따라 일정하기 때문에 S4 모델은 Linear Time Invariance(LTI) 시스템된다. LTI 시스템은 정적 convolution을 사용하기 때문에 계산 효율적이지만, 관련 있는 정보와 무관한 정보를 구별하는 능력이 없어서 긴 시퀀스에 취약하다는 단점이 존재한다. Mamba는 이것을 selective mechanism을 이용해서 개선한 Selective SSM(S6)를 제안한다.
참고로 S4 모델이 Structured라는 이름이 붙은 이유는 이 모델이 행렬 A\bold{A}에 특별한 구조를 부여하기 때문이다. 이에 대해 인기 있는 형태는 대각행렬이고 이것은 S6에서도 사용된다.

Selective SSM(S6)

Selective SSM(S6)는 S4의 LTI 속성이 가진 한계를 selective mechanism을 통해 개선한 모델이다. —S가 6개가 아닌데 이름이 S6인 이유는 S4 다음에 S5라는 모델이 있었기 때문.
S4 모델이 꽤 우수한 성능을 보였지만 관련 있는 정보와 무관한 정보를 구별하는 능력이 없어서 긴 시퀀스에 취약하다는 단점이 존재했는데, 그것은 계산 효율성을 위해 정적 convolution을 사용한 LTI 시스템의 근본적인 한계 때문이다. 이를 해결하기 위해 S6은 S4와 동일한 파라미터를 사용하지만 Δ,B,C\Delta, \bold{B}, \bold{C}를 보다 입력에 의존하도록 다음과 같이 정의한다.
B:(B,L,N)←sB(x)C:(B,L,N)←sC(x)Δ:(B,L,D)←τΔ(Parameter+sΔ(x))\begin{aligned} \bold{B} : (B, L, N) &\leftarrow s_B(x) \\ \bold{C} : (B, L, N) &\leftarrow s_C(x) \\ \Delta : (B, L, D) &\leftarrow \tau_\Delta(\text{Parameter} + s_\Delta(x)) \end{aligned}
Δ,B,C\Delta, \bold{B}, \bold{C}를 학습되도록 함으로써 모델은 상태, 입력, 출력에 대해 중요한 정보를 남기고 관련 없는 정보를 무시하도록 학습될 수 있다. 이 중에서 Δ\Delta는 A,B\bold{A}, \bold{B} 중 어느 것에 초점을 맞출지를 결정하도록 학습 되고—A,B\bold{A}, \bold{B}가 동일한 Δ\Delta와 곱해지지만, A\bold{A}가 음의 상수를 취하기 때문에 B\bold{B}와 역관계가 된다—, B\bold{B}는 입력 xtx_t를 상태 hth_t로 보낼지 여부를 결정하도록 학습되고, C\bold{C}는 상태를 출력 yty_t로 내보낼지 여부를 결정하도록 학습된다. 이것이 바로 selective mechanism이다.
실제 구현에서 sB(x)=LinearN(x),sC(x)=LinearN(x),sΔ(x)=BroadcastD(Linear1(x)),τΔ=softpluss_B(x) = \text{Linear}_N(x), s_C(x) = \text{Linear}_N(x), s_\Delta(x) = \text{Broadcast}_D(\text{Linear}_1(x)), \tau_\Delta = \text{softplus}를 설정한다. 이에 반해 A\bold{A}는 상수값을 갖도록 설정된다.
여기서 sΔs_\Delta와 τΔ\tau_\Delta를 위와 같이 선택한 이유는 RNN gating 메커니즘과의 연결 때문이다. 즉, N=1,A=−1,B=1,sΔ=Linear(x),τΔ=softplusN = 1, \bold{A} = -1, \bold{B} = 1, s_\Delta = \text{Linear}(x), \tau_\Delta = \text{softplus}일 때 selective SSM recurrence는 다음 형식을 취한다. —이에 대한 유도는 AI/ Paper/ Mamba/ Appendix 참조
ht=A‾ht−1+B‾xt=(1−σ(Linear(xt)))ht−1+σ(Linear(xt))xt=(1−gt)ht−1+gtxt\begin{aligned} h_t &= \overline{A}h_{t-1} + \overline{B}x_t \\ &= (1 - \sigma(\text{Linear}(x_t)))h_{t-1} + \sigma(\text{Linear}(x_t))x_t \\ &= (1-g_t)h_{t-1} + g_t x_t\end{aligned}
여기서 gt=σ(Linear(xt))g_t = \sigma(\text{Linear}(x_t))는 이전 잠재 상태 ht−1h_{t-1}과 현재 입력 xtx_t 사이에 어떤 것에 더 초점을 맞출지를 결정하는 gating 역할을 하게 된다. 즉 gtg_t의 값이 0에 가까워지면 이전 은닉에 초점을 맞추게 되고, gtg_t의 값이 1에 가까워지면 현재 입력에 초점을 맞추게 된다.
위의 변경으로 인한 S4와 S6의 알고리즘 차이는 아래 참조. selective mechanism의 도입 때문에 S6의 6번째 단계에서 convolution을 사용할 수 없고 시간 가변인 recurrence만 가능하다.
Algorithm 1 SSM (S4)
Input: x:(B,L,D)x : (B, L, D)
Output: y:(B,L,D)y : (B, L, D)
1.
A:(D,N)←Parameter\bold{A} : (D, N) \leftarrow \text{Parameter} // 구조화된 N×NN \times N 행렬을 나타냄
2.
B:(D,N)←Parameter\bold{B} : (D, N) \leftarrow \text{Parameter}
3.
C:(D,N)←Parameter\bold{C} : (D, N) \leftarrow \text{Parameter}
4.
Δ:(D)←τΔ(Parameter)\Delta : (D) \leftarrow \tau_\Delta(\text{Parameter})
5.
A‾,B‾:(D,N)←discretize(Δ,A,B)\overline{\bold{A}},\overline{\bold{B}} : (D, N) \leftarrow \text{discretize}(\Delta, \bold{A},\bold{B})
6.
y←SSM(A‾,B‾,C)(x)y \leftarrow \text{SSM}(\overline{\bold{A}},\overline{\bold{B}}, \bold{C})(x) // time-invariant: recurrence 또는 convolution
7.
return yy
Algorithm 2 SSM + Selection (S6)
Input: x:(B,L,D)x : (B, L, D)
Output: y:(B,L,D)y : (B, L, D)
1.
A:(D,N)←Parameter\bold{A} : (D, N) \leftarrow \text{Parameter} // 구조화된 N×NN \times N 행렬을 나타냄
2.
B:(B,L,N)←sB(x)\bold{B} : (B, L, N) \leftarrow s_B(x)
3.
C:(B,L,N)←sC(x)\bold{C} : (B, L, N) \leftarrow s_C(x)
4.
Δ:(B,L,D)←τΔ(Parameter+sΔ(x))\Delta : (B, L, D) \leftarrow \tau_\Delta(\text{Parameter} + s_\Delta(x))
5.
A‾,B‾:(B,L,D,N)←discretize(Δ,A,B)\overline{\bold{A}},\overline{\bold{B}} : (B, L, D, N) \leftarrow \text{discretize}(\Delta, \bold{A},\bold{B})
6.
y←SSM(A‾,B‾,C)(x)y \leftarrow \text{SSM}(\overline{\bold{A}},\overline{\bold{B}}, \bold{C})(x) // time-varying: recurrence (scan) only
7.
return yy

Hardware-aware Algorithm

Selective 메커니즘을 도입하여 무관한 정보를 무시하고 관련 있는 정보에 집중하여 긴 시퀀스에 대해서도 좋은 성능을 발휘할 수 있지만, S4와 같은 LTI 시스템이 갖고 있는 정적 convolution을 사용하여 얻을 수 있는 효율적인 계산에 대한 이점을 잃게 되었다.
이에 대한 해결책으로 Mamba 연구진들은 Hardware-aware라 부르는 소프트웨어적 기법들을 도입하여 모델의 성능 개선을 시도한다. 구체적으로 Kernel Fusion, Parallel Scan, Recomputation이 그것인데, 상세 내용은 개별 페이지 참조

Mamba

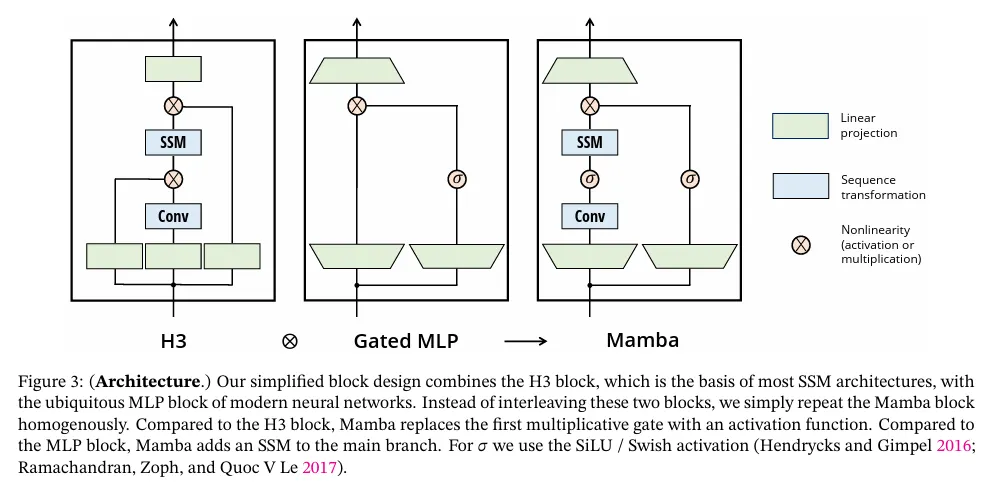
Mamba 자체는 위에 정의된 S6 모델을 이용하는 신경망 아키텍쳐를 의미한다. 이것은 기존에 SSM 아키텍쳐로 널리 쓰이던 H3 아키텍쳐와 Gated MLP를 결합한 구조이다. 아래 그림 참조
Mamba 연구진들은 S6 모델과 Mamba 아키텍쳐를 이용하여 Mamba가 Attention-free로 Transformer의 성능을 능가한 최초의 모델이라고 주장함.

Sample Code

이하 코드는 Mamba 논문에 구현된 코드를 참조한다. 원본 코드는 CUDA 코드를 이용한 최적화 기법을 사용하여 상당히 복잡하기 때문에 흐름만 정리. 자세한 내용은 저자들이 공개한 원본 코드 참조
mamba
state-spaces

Model

모델은 다음의 파라미터들로 구성된다.
# 최초 입력에 대한 선형 변환 self.in_proj = nn.Linear() # [Conv block] # 선형 변환 후 분할 된 입력에 대해 conv 연산과 silu 수행. # 이 둘은 causal_conv1d로 대체될 수 있음 self.conv1d = nn.Conv1d() self.act = nn.SiLU() # [SSM block] # 분할 된 입력에 대한 선형 변환 self.x_proj = nn.Linear() self.dt_proj = nn.Linear() # SSM에 사용되는 상수 파라미터 A. 1부터 d_state까지 1씩 증가한다. # 수치적 안정성을 위해 log를 취한다음 실제 사용될 할는 -exp()를 씌워서 사용 A_log = torch.log(A) # SSM block의 skip connection 파라미터 self.D = nn.Parameter() # SSM block을 통과한 결과와 최초 분할된 입력을 합친 결과를 induction head로 합치고 출력 self.out_proj = nn.Linear()
Python
복사

Forward

Mamba 아키텍쳐에 따라 흐름 정리. 이하 코드는 이해를 돕기 위해 작성한 부분을 참고하며, 실행은 cuda를 이용해 구현된 부분을 따라간다.
1.
우선 임베딩된 입력 또는 이전 레이어의 출력이 주어지면 선형 변환을 수행한다.
# We do matmul and transpose BLH -> HBL at the same time xz = rearrange( self.in_proj.weight @ rearrange(hidden_states, "b l d -> d (b l)"), "d (b l) -> b d l", l=seqlen, ) if self.in_proj.bias is not None: xz = xz + rearrange(self.in_proj.bias.to(dtype=xz.dtype), "d -> d 1")
Python
복사
2.
상수 파라미터 A\bold{A}의 log에 대해 음의 exp()를 취해 실제 사용할 값으로 변환한다.
A = -torch.exp(self.A_log.float()) # (d_inner, d_state)
Python
복사
3.
Induction Head를 위해 입력을 둘로 분할 한다.
x, z = xz.chunk(2, dim=1)
Python
복사
4.
분할한 입력에 대해 Conv와 활성화 함수(silu)을 수행한다. 만일 causal convolution을 사용하면 대신 causal conv 함수를 실행한다.
# Compute short convolution if conv_state is not None: # If we just take x[:, :, -self.d_conv :], it will error if seqlen < self.d_conv # Instead F.pad will pad with zeros if seqlen < self.d_conv, and truncate otherwise. conv_state.copy_(F.pad(x, (self.d_conv - x.shape[-1], 0))) # Update state (B D W) if causal_conv1d_fn is None: x = self.act(self.conv1d(x)[..., :seqlen]) else: assert self.activation in ["silu", "swish"] x = causal_conv1d_fn( x=x, weight=rearrange(self.conv1d.weight, "d 1 w -> d w"), bias=self.conv1d.bias, activation=self.activation, )
Python
복사
5.
conv를 통과시킨 입력을 SSM 블럭에 넣기 전에 선형 변환을 수행한 후에 Δ,B,C\Delta, \bold{B}, \bold{C} 파라미터로 분할한다음 Δ\Delta에 대해 추가로 Linear의 가중치와 행렬곱을 수행하여 차원을 조정한다.
•
이것은 sB(x)=LinearN(x),sC(x)=LinearN(x),sΔ(x)=BroadcastD(Linear1(x))s_B(x) = \text{Linear}_N(x), s_C(x) = \text{Linear}_N(x), s_\Delta(x) = \text{Broadcast}_D(\text{Linear}_1(x))를 구현한 것에 해당한다.
# We're careful here about the layout, to avoid extra transposes. # We want dt to have d as the slowest moving dimension # and L as the fastest moving dimension, since those are what the ssm_scan kernel expects. x_dbl = self.x_proj(rearrange(x, "b d l -> (b l) d")) # (bl d) dt, B, C = torch.split(x_dbl, [self.dt_rank, self.d_state, self.d_state], dim=-1) dt = self.dt_proj.weight @ dt.t() dt = rearrange(dt, "d (b l) -> b d l", l=seqlen) B = rearrange(B, "(b l) dstate -> b dstate l", l=seqlen).contiguous() C = rearrange(C, "(b l) dstate -> b dstate l", l=seqlen).contiguous()
Python
복사
6.
Δ\Delta에 대해 softplus를 수행한다.
•
이것은 τΔ=softplus\tau_\Delta = \text{softplus}를 구현한 것에 해당한다.
delta = delta.float() if delta_bias is not None: delta = delta + delta_bias[..., None].float() if delta_softplus: delta = F.softplus(delta)
Python
복사
(입력과 A, B, C에 대해 실수와 복소수 관련 타입 정리하는 부분 생략)
7.
A‾=exp⁡(ΔA)\overline{\bold{A}} = \exp(\Delta \bold{A})를 따라 A\bold{A}를 이산화 한다.
deltaA = torch.exp(torch.einsum('bdl,dn->bdln', delta, A))
Python
복사
8.
B\bold{B}는 Δ\Delta와 곱해 이산화 한다. 추가로 입력 u\bold{u}은 고정되어 있기 때문에 미리 곱한다.
•
이것은 B‾=(ΔA)−1(exp⁡(ΔA)−I)⋅ΔB\overline{\bold{B}} = (\Delta \bold{A})^{-1}(\exp(\Delta\bold{A}) -\bold{I})\cdot \Delta \bold{B} 로 B\bold{B}를 이산화하는 S4의 ZOH 방식과 다르다. 여기서 B\bold{B}가 통과하는 Linear는 위의 결과를 근사하도록 학습되는 것으로 생각할 수 있다.
# B가 실수인 경우와 복소수인 경우에 대해 구별해서 처리. if not is_variable_B: deltaB_u = torch.einsum('bdl,dn,bdl->bdln', delta, B, u) else: if B.dim() == 3: deltaB_u = torch.einsum('bdl,bnl,bdl->bdln', delta, B, u) else: B = repeat(B, "B G N L -> B (G H) N L", H=dim // B.shape[1]) deltaB_u = torch.einsum('bdl,bdnl,bdl->bdln', delta, B, u)
Python
복사
(C의 차원을 정리하는 부분 생략)
9.
시간 고정적이어서 conv를 사용할 수 있던 S4와 달리 시간 가변적이므로 S6는 다음과 같이 scan 연산을 수행해야 한다. 각 단계에서 A‾\overline{\bold{A}}와 B‾\overline{\bold{B}}를 이용하여 상태 hth_t를 업데이트하고, 업데이트 된 상태와 C\bold{C}를 곱해 출력 yty_t를 계산한다.
ht=A‾ht−1+B‾xtyt=Cht\begin{aligned} h_t &= \overline{\bold{A}}h_{t-1} + \overline{\bold{B}}x_t \\ y_t &= \bold{C}h_t \end{aligned}
last_state = None x = A.new_zeros((batch, dim, dstate)) # 0으로 초기화. 이것은 A의 device와 dtype을 갖는다. ys = [] for i in range(u.shape[2]): x = deltaA[:, :, i] * x + deltaB_u[:, :, i] if not is_variable_C: y = torch.einsum('bdn,dn->bd', x, C) else: if C.dim() == 3: y = torch.einsum('bdn,bn->bd', x, C[:, :, i]) else: y = torch.einsum('bdn,bdn->bd', x, C[:, :, :, i]) if i == u.shape[2] - 1: last_state = x if y.is_complex(): y = y.real * 2 ys.append(y) # ys를 하나로 합친다. y = torch.stack(ys, dim=2) # (batch dim L)
Python
복사
10.
SSM skip connection 파라미터가 있었으면 출력을 업데이트 한다.
out = y if D is None else y + u * rearrange(D, "d -> d 1")
Python
복사
11.
SSM 블록의 마지막에서 3에서 분할 했던 입력을 silu()를 통과시켜서 출력에 합친다.
if z is not None: out = out * F.silu(z)
Python
복사
12.
SSM 블록을 통과해서 얻은 최종 결과를 Induction Head로 합친 후에 결과를 반환한다.
out = self.out_proj(y)
Python
복사

참고

[Paper Review] Mamba: Linear-Time Sequence Modeling with Selective State Spaces
발표자 : 석사과정 천재원 1. 논문 제목: Mamba: Linear-Time Sequence Modeling with Selective State Spaces 2. 논문 링크: https://arxiv.org/abs/2312.00752 3. 인용 수: 143회 (~2024.3.31) 4. 논문 Overview: - Structured SSM 계열의 연구로, Selectivity에 대한 컴포넌트를 추가함으로써 높은 수준의 성능 향상을 이끌어 냄 - Hardware-aware Computation(Scan)을 사용하여 빠르게 Recurrence를 계산 - Language Modelling의 헤게모니인 Transformer에 비견될 정도의 성능을 보여줌
https://www.youtube.com/watch?v=JjxBNBzDbNk
Made with