튜링 기계
테이프 위를 움직이며, 테이프에 쓰여진 기호를 읽고 명령을 수행하는 기계.
튜링 기계에는 한 번에 하나의 상태만 가질 수 있는 –현대의 컴퓨터– 결정론적 튜링 기계와 한 번에 여러 상태를 동시에 가질 수 있는 –양자 컴퓨터– 비결정론적 튜링 기계가 있다.
비결정론적 튜링 기계는 분기 상황을 한 번에 진행할 수 있기 때문에, 결정론적 튜링 기계로 지수 시간이 걸리는 문제를 다항식 시간내에 해결할 수 있다. —지수 함수에 Log를 씌웠다고 생각하면 된다.
튜링 기계 –명령을 수행하는 방식– 를 폰 노이만 구조 –CPU, 메모리, 프로그램으로 구분된– 로 만들어낸 것이 현대의 컴퓨터라고 할 수 있다.
결정 문제 (Decision Problem)
Yes or No로 대답할 수 있는 문제.
‘n개의 도시를 모두 방문하고 돌아오는 최단거리를 구하라’는 문제는 Yes, No로 대답할 수 없지만, ‘n개의 도시를 모두 방문하고 돌아오는 거리 K이하인 경로가 존재하는가?’ 는 Yes, No로 대답할 수 있으므로 결정문제다.
P와 NP는 모두 결정 문제에 속한다.
다항 시간
다항 시간이라는 것은 현실적인 시간 내에 해결 가능한 시간을 의미한다. 문제 해결 자체는 가능하지만 해결하는데 시간이 초 정도의 시간이 걸린다면 현실적으로 해결하기 어려운 시간이라는 의미다. –참고로 우주의 나이는 이다. 다항 시간을 넘어서는 시간을 지수 시간이라고 한다.
일반적으로 다항식하면 이 포함되지만, 알고리즘에서 다항 시간은 알고리즘 함수의 최고차 항의 계수가 3이하이거나 으로 표시되는 정도까지 인정한다. 지수 범위가 5만 넘어가도 현실적인 시간 내에 풀기는 어려우므로 다항식 시간이라고 보기는 어렵다.
P (Polynomial time)
결정론적 튜링 기계를 사용해 다항 시간 내에 답을 구할 수 있는 문제의 집합.
NP (Non-deterministic Polynomial time)
비결정론적 튜링 기계를 사용해 다항 시간 내에 답을 구할 수 있는 문제의 집합. 또는 Yes라는 근거가 제시되었을 때 결정론적 튜링 기계로 그것이 옳다는 것을 다항식 시간에 확인할 수 있는 문제의 집합.
위 2가지 설명은 완전히 동일한 의미이다. 비결정론적 튜링 기계로 다항 시간 내에 답을 구할 수 있다는 것은 결정론적 튜링 기계로는 답을 구하는데 지수 시간이 걸린다는 것이고, 결정론적 튜링 기계로 지수 시간이 걸린다는 것은 Yes라는 근거가 제시되었을 때 다항식 시간에 그것이 옳다는 것만 확인할 수 있다는 뜻이 된다. 모두 같은 말인데, NP 문제를 설명할 때 표현이 다르니 주의.
NP는 풀 수 없는 문제가 아니라 풀 수 있는데 –Yes라는 근거가 제시되므로– 튜링 기계로 다항식 시간 내에 풀 수 있는 알고리즘이 아직 알려지지 않은 문제이다. 운이 좋으면 다항식 시간 내에 답을 구할 수 있기도 하다.
NP Hard
다른 모든 NP 문제로 다항식 시간 내에 변환(Reduction) 가능한 문제를 NP-Hard 라고 부른다. TSP 문제는 해밀토니안 문제로 변환가능하기 때문에 NP-Hard 문제가 된다.
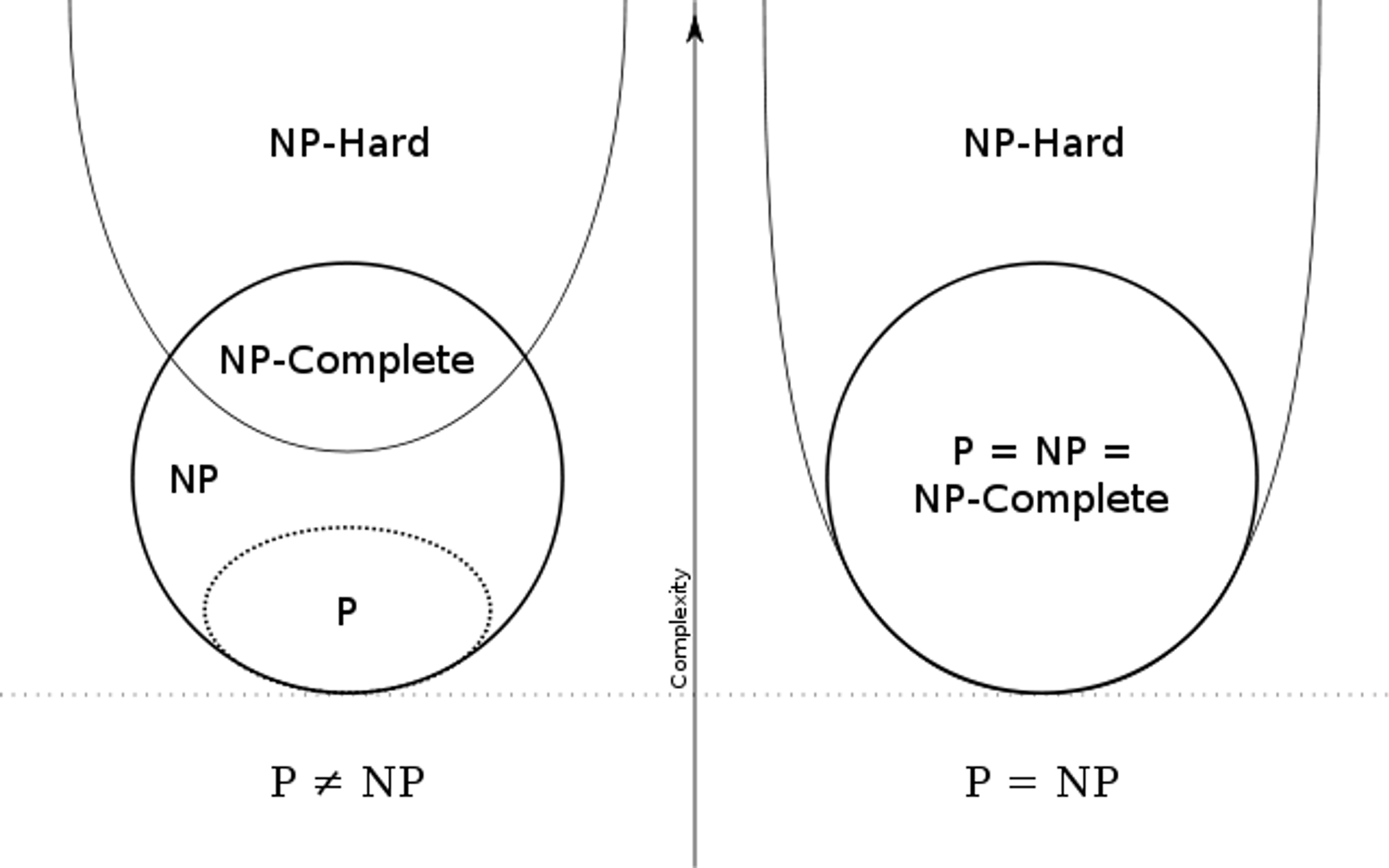
NP 문제로 변환할 수 있는 경우 NP-Hard가 된다고 해서 NP-Hard가 NP의 부분집합처럼 생각되는데, NP-Hard는 결정문제 뿐만 아니라 비결정문제도 포함되기 때문에 NP의 부분집합이 아니다. 그래서 ‘모든 경우를 일일히 확인하지 않고서는 답을 구할 수 없는 문제’라는 보다 정의가 좀 더 직관적으로 느껴진다. 참고로 NP문제와 NP-Hard의 교집합은 NP-Complete이 된다. —문서 상단의 이미지 참조
NP-Hard는 모든 NP 문제로 변환 할 수 있기 때문에 NP-Hard 문제를 다항식 시간 내에 해결할 수 있다면, NP 문제는 ‘변환하는데 걸리는 다항식 시간 + 변환한 문제를 해결하는데 걸리는 다항식 시간’이 되어 결국 다항식 시간 내에 풀리는 문제가 된다. –쉽게 말해서 어려운 문제를 풀면 그것과 관련된 쉬운 문제는 저절로 풀린다는 것.
NP-Hard는 P와 교집합이 없다고 여겨지는데, 만일 단 한 문제라도 P 문제이면서 NP-Hard인 문제가 발견되면, –NP-Hard 문제는 모든 NP 문제로 변환할 수 있기 때문에– 그 NP-Hard 문제를 이용하여 모든 NP 문제를 P 문제로 변환할 수 있게 되고 P = NP가 성립된다. –TSP 문제를 다항식 시간 내에 풀 수 있는 알고리즘이 발견되면 이것이 성립한다.
NP Complete
NP이면서 동시에 NP Hard인 –교집합– 문제. 일반적으로 NP 문제 중 가장 어려운 문제들의 집합이라고 한다.
NP-Complete 문제들은 NP-Hard 문제인데, 정의상 NP-Hard 문제는 모든 NP 문제로 변환 가능하기 때문에, 만일 NP-Complete에 속하는 문제 중 어느 한 문제만이라도 다항식 시간 내에 해결이 된다면, 그 해법을 이용하여 NP에 속하는 다른 모든 문제를 다항식 시간에 풀 수 있다.
P-NP 문제
결정론적 튜링 기계로 답을 구할 수 있는 모든 문제는 비결정론적 튜링 기계로 다항식 시간 내에 구할 수 있는 반면 그 반대는 아니므로 P는 NP의 부분집합이다.
그런데 P가 NP의 부분집합이라는 것은 확실하지만 P가 NP보다 작다는 증명이 되지 않았기 때문에, P와 NP가 같은지 P가 NP보다 작은지는 알 수 없다. 이게 바로 P-NP 문제이다.
만일 P와 NP가 같다는 것이 증명되면 모든 NP 문제는 P 문제로 변환할 수 있는 알고리즘이 존재한다는 뜻이고 모든 NP 문제는 결정론적 튜링 기계로 다항식 시간 내에 답을 구할 수 있다는 뜻이 된다.
이것은 직관적으로 믿기 어렵기 때문에 많은 사람들이 P와 NP가 같지 않다고 믿는다.