Energy-Based Model(EBM)
Energy Based Model(EBM)은 데이터 포인트의 확률을 Energy 함수를 사용하여 모델링하는 방식이다. 여기서 Energy는 데이터 포인트의 품질이나 가능성을 나타내는 스칼라 값으로 낮은 에너지 값은 모델이 데이터 포인트를 더 선호하거나 그 데이터 포인트의 가능성이 더 높음을 의미한다. 높은 에너지는 그 반대다.
EBM은 다음과 같은 Gibbs 분포로 작성할 수 있다.
여기서 은 파라미터 를 갖는 energy 함수이고, 는 분할 함수(partition function) 또는 정규화 상수라고 하며 확률이 1이 되도록 한다. 은 에 관하여 상수이지만 의 함수이며, 일반적으로 마르코프 가정을 만들지 않기 때문에 이 적분을 평가하는 것이 까다롭다. 따라서 EBM은 Annealed Importance Sampling 같은 근사 방법을 사용하여 정규화 상수의 계산을 피한다.
EBM의 이점은 에너지 함수가 음이 아닌 스칼라를 반환하는 함수면 되고, 정규화 상수 계산 하지 않기 때문에 적분해서 1이 될 필요도 없다는 것이다. 이것은 변환된 분포가 여전히 유효한 확률 분포여야 하는 Normalizing Flow 모델과 대비된다. 때문에 다양한 신경망 아키텍쳐를 사용할 수 있다.
Training
EBM이 자유롭게 아키텍쳐를 선택할 수 있기 때문에 EBM에 대한 특정 아키텍쳐보다는 모델의 학습하는 부분에 초점을 맞춘다.
식 (1)에 대한 log 확률의 gradient는 다음과 같이 2개의 합으로 구분된다.
여기서 첫 번째 항 은 자동 미분을 사용하여 간단하게 평가할 수 있지만 두 번째 항 은 종종 계산하기 까다롭기 때문에 근사해야 한다.
이러한 EBM에 대한 학습을 위해 Langevin MCMC나 Contrastive Divergence(CD), Score Matching, Noise Contrastive Estimation(NCE)과 같은 방법을 사용할 수 있다. 개별 페이지 참조.
Example: products of experts(PoE)
에너지 기반 모델의 예로 실내 온도에서 열적으로 안정적이고 COVID-19 spike 수용체에 결합되는 단백질의 생성 모델을 만든다고 가정하자. 가 안정적인 단백질을 생성할 수 있고 가 결합하는 단백질을 생성할 수 있다고 가정하자. 이러한 모델 각각을 expert로 볼 수 있다. 그 자체로는 데이터의 충분한 모델이 아니지만 product of experts(PoE)를 계산하여 결합하면 conjuction of feature를 표현할 수 있다.
이것은 안정적이고 결합하는 단백질에 높은 확률을 할당하고 나머지에는 낮은 확률을 할당한다. 반면 mixture of expert(MoE)는 또는 모두에서 생성할 수 있지만 그 둘의 feature를 결합할 수는 없다.
전문가를 EBM으로 표현하면 PoE 모델은 EBM이거 에너지는 다음과 같이 주어진다.
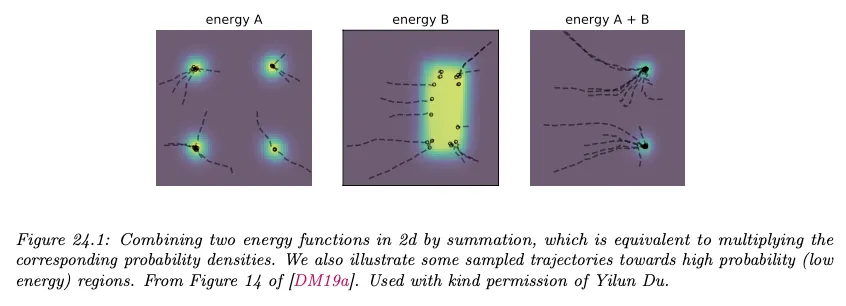
직관적으로 에너지의 각 구성성분을 데이터에 ‘soft constraint’로 생각할 수 있다. 아래 그림 참조.