•
머신러닝을 실제로 할 때 생각해 봐야 할 것들.
•
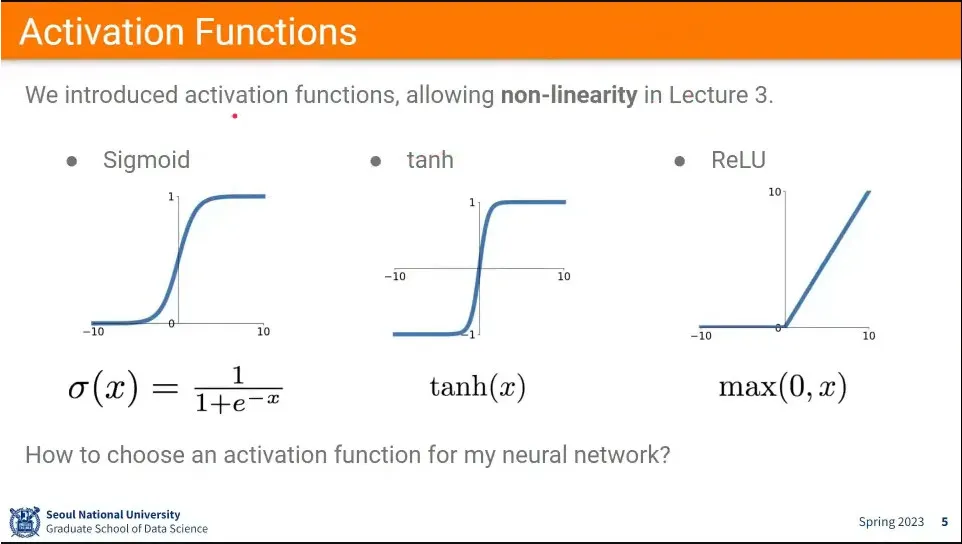
함수를 비선형으로 만들어주는 activation 함수들은 sigmoid, tanh, relu를 많이 씀.
•
뉴럴 네트워크에서는 sigmoid를 많이 썼음.
•
딥뉴럴 네트워크 들어오면서 gradient를 죽이는 문제로 인해 요즘은 잘 안 씀.
◦
추가로 zero-centered output이 안 나오는게 문제
•
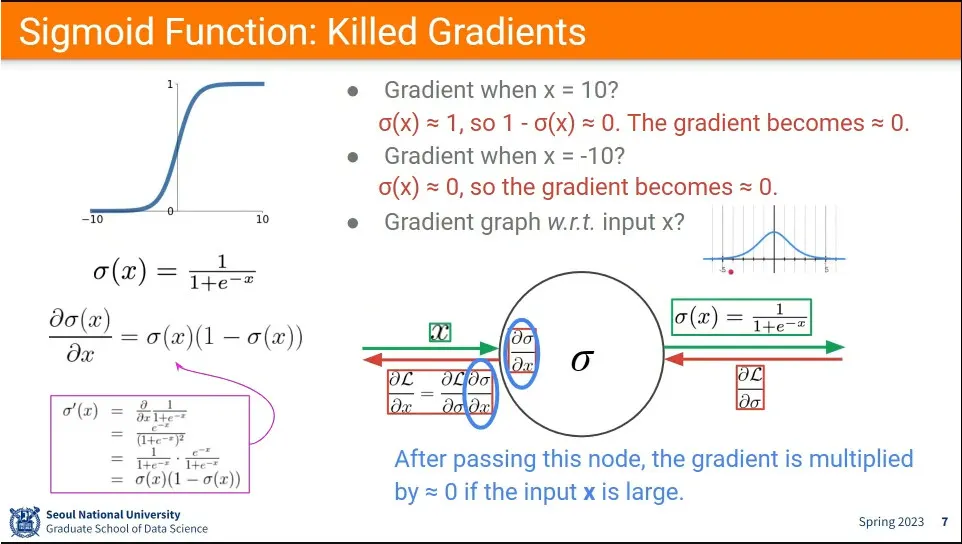
sigmoid 함수 특성상 절대값이 5 정도만 넘어도 0에 가까운 결과가 나옴.
◦
따라서 역전파 할 때 sigmoid 앞에 있는 레이어들은 학습이 잘 안되는 문제가 발생
•
sigmoid가 zero-centered output이 안 나오기 때문에 결과의 부호를 못 바꿈
◦
그렇기 때문에 오른쪽 아래 그래프처럼 optimal이 존재하는 경우 그 경로를 못 따라가고 지그재그로 따라가게 되서 비효율적.
◦
물론 mini-batch로 묶고 평균 내서 하기 때문에 이런 경우는 많지 않음.
•
뉴럴 네트워크의 layer 깊이가 깊지 않을 때는 문제가 드러나지 않았는데, deep 뉴럴 네트워크가 되면서 문제가 드러남.
•
Tanh는 Sigmoid와 달리 zero-centered라서 non zero-centered output 문제는 해결했으나, 본질적으로 sigmoid 함수와 같기 때문에 killing gradient 문제가 존재함.
•
ReLU는 계산이 효율적이고, 값이 커지면 0으로 수렴하는 문제도 사라짐
•
그러나 zero-centered output이 아니고, 0에서 미분이 안되는 문제가 있음. 더 큰 문제는 초기값이 음수면 학습이 아예 안 됨.
•
ReLU의 단점을 해결한 버전. 음수일 때도 값을 좀 준다.
◦
문제는 그 주는 값을 얼마나 주는지가 문제.
•
또 다른 ReLU 개선 버전. zero mean output 문제도 해결하고 —값이 zero centered에 가깝게 나오도록 디자인 됨
•
하나 문제는 exp() 계산 비용이 비싸다는 것.
•
보통 처음에는 ReLU를 쓰고, 어느 정도 학습이 되면 Leaky ReLU나 ELU를 바꿔서 성능이 좋아지는지를 본다.
•
sigmoid나 tanh는 안 씀
•
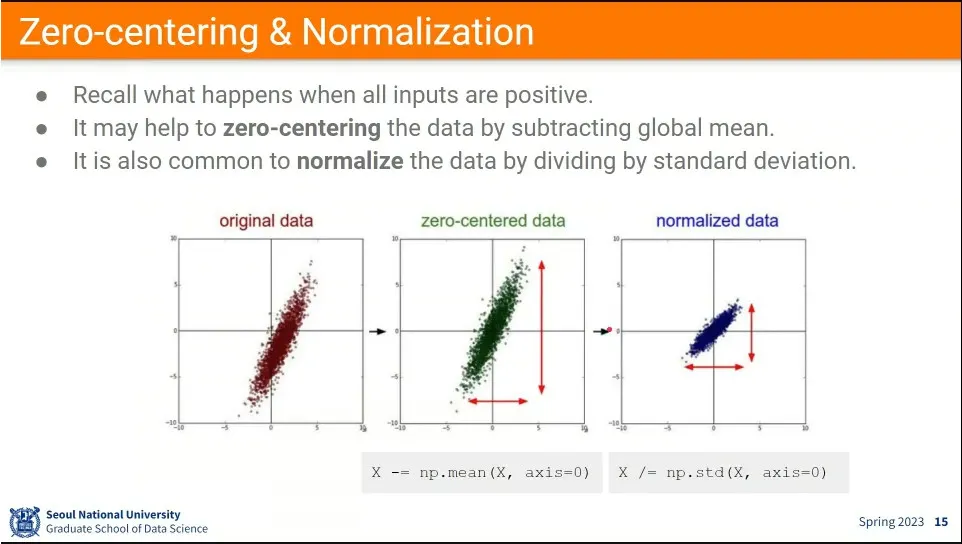
activation 함수의 output이 zero-centered가 안나오기 때문에, 아예 input을 zero-cented로 만든 후에 넣음.
◦
추가로 정규화까지 한다. —정규화는 각 dimension의 영향력을 동일하게 맞춰주는 것.
•
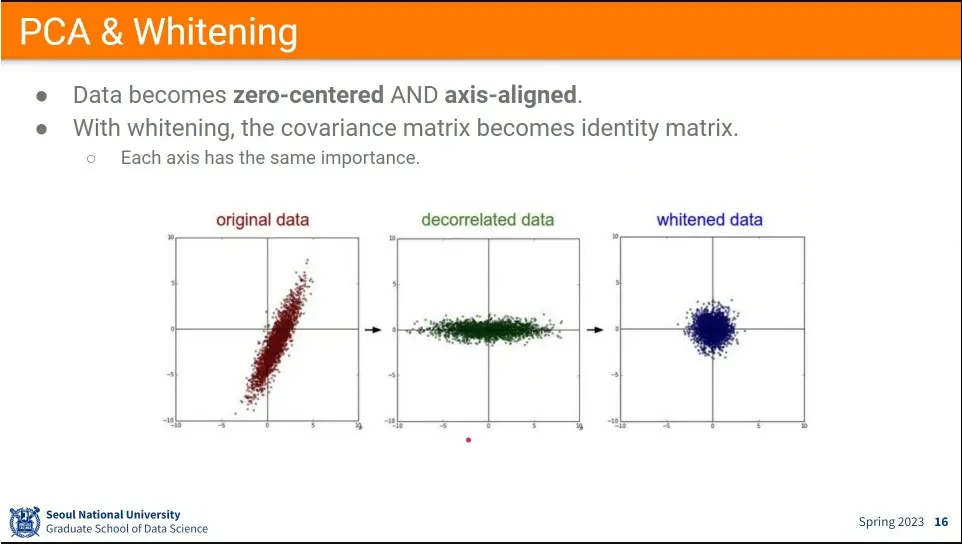
decorrelation은 input 데이터를 zero-centered 하면서 영향을 주는 축 중심으로 aligned 되도록 하는 것.
◦
가장 큰 영향력을 주는 dimension과 그 다음 영향력을 주는 dimension을 뽑아 정렬한다.
•
whitening은 decorrelation 한 결과에 대해 분산으로 나눠주면 가우시안 분포처럼 만들 수 있다.
•
PCA는 딥러닝 시기 전에 많이 쓰던 방법. 데이터는 보존하면서 Dimension을 줄이는 방법 (차원 축소)
1.
우선 zero-centered를 시킨다. —데이터셋 평균으로 데이터를 뺌
2.
그 후에 covariance matrix를 구한다. —자기 자신에 대해 외적을 구함
3.
그 후에 eigenvalue decomposition을 함.
4.
그렇게 구해진 정렬된 결과에서 원하는 만 남기고 나머지는 없애면 차원 축소가 됨. 2개만 남기면 2차원으로 줄어듬.
•
실제 적용 예
◦
유튜브 할 때 PCA를 썼는데, 비디오 데이터는 양이 크기 때문에 해 줬음.
•
원본 데이터에 대해 변형을 줘서 학습 시킴.
◦
사람이 보기에 동일하지만, 컴퓨터는 다르게 처리하는 데이터를, 사실 같은 데이터라는 것을 학습하도록 함.
◦
이러면 적은 데이터로도 많은 학습 데이터량을 만들 수 있음
•
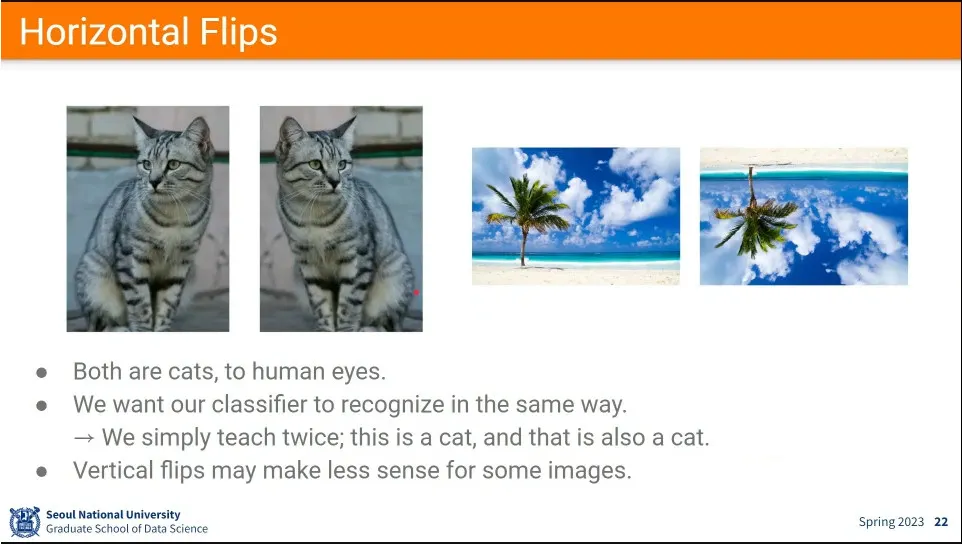
가장 쉬운 예가 좌우 반전.
◦
상하 반전은 중력 때문에 잘 안 함.
•
이미지 내에서 랜덤한 영역 crop
•
scaling도 많이 함.
•
실제적인 사용 방식
◦
학습할 때는 patch size를 기준으로 무작위로 잘라서 학습 시킴
◦
테스트 할 때는 여러군데 잘라서 돌린 후에 결과를 평균 냄.
•
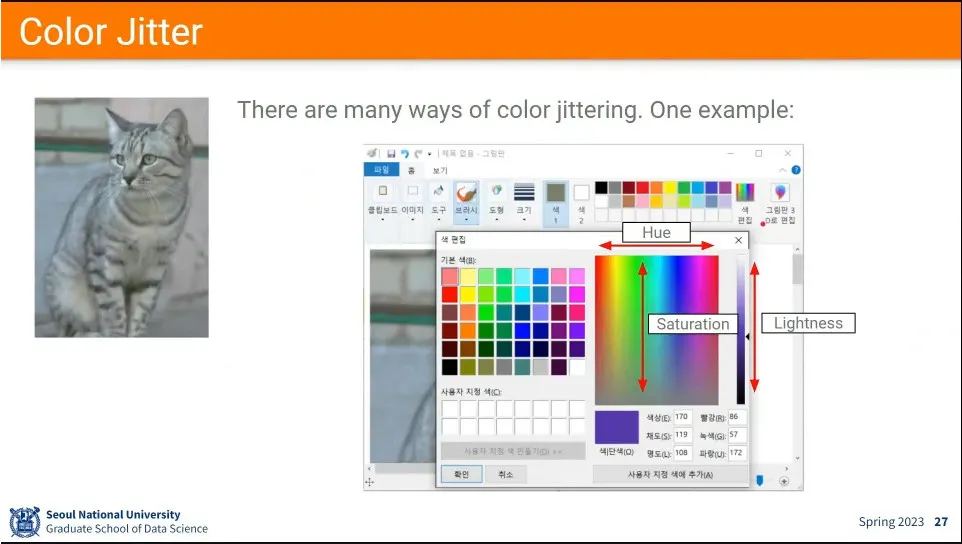
조명이 달라진 것도 data augmentation으로 사용함.
•
조명 바꾸는 것은 HSV를 이용.
•
다양한 Data augmentation 방법
•
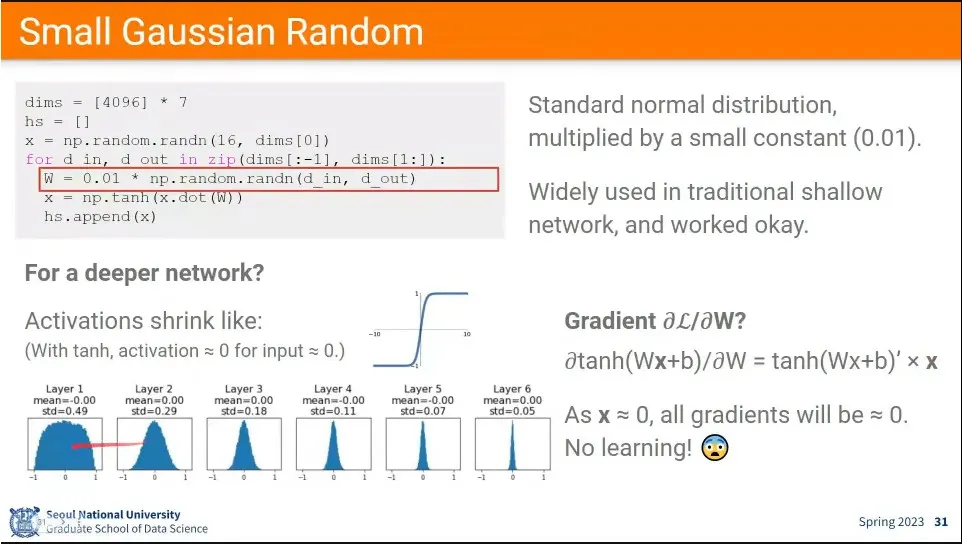
가우시안 랜덤을 작게 해서 초기화 했더니, Layer가 깊어지면서 0으로 수렴하는 문제가 발생
•
이번에는 가우시안 랜덤 값을 크게 해서 초기화 했더니 Layer가 깊어지면서 1, -1로 수렴하는 문제가 발생. 이 경우에도 미분하면 0으로 수렴하게 됨
•
Xavier 초기화 방법은 랜덤값을 input의 제곱근을 씌운 것으로 나누는 것
◦
이러면 0으로 수렴하는 문제를 완화할 수 있음.
•
Xavier 초기화 유도 과정
◦
iid assumption과 W, x의 기댓값이 0이라는 가정을 이용하여 식을 전개 함.
◦
최종적으로 W의 분산을 으로 하면 input과 output의 분산이 비슷하다는 결론이 나옴.
•
ReLU도 그냥 초기화를 하면 0으로 수렴하는 문제가 발생
•
ReLU에 대해서는 Kaiming/MSRA 초기화 방법을 씀.
◦
input의 dimension의 역수에 2를 곱한 값에 제곱근을 씌워 사용함.
◦
그러면 0으로 수렴하는 문제가 완화된다.
•
초기화 문제는 딥러닝 시작 후에 계속 연구되어 옴
•
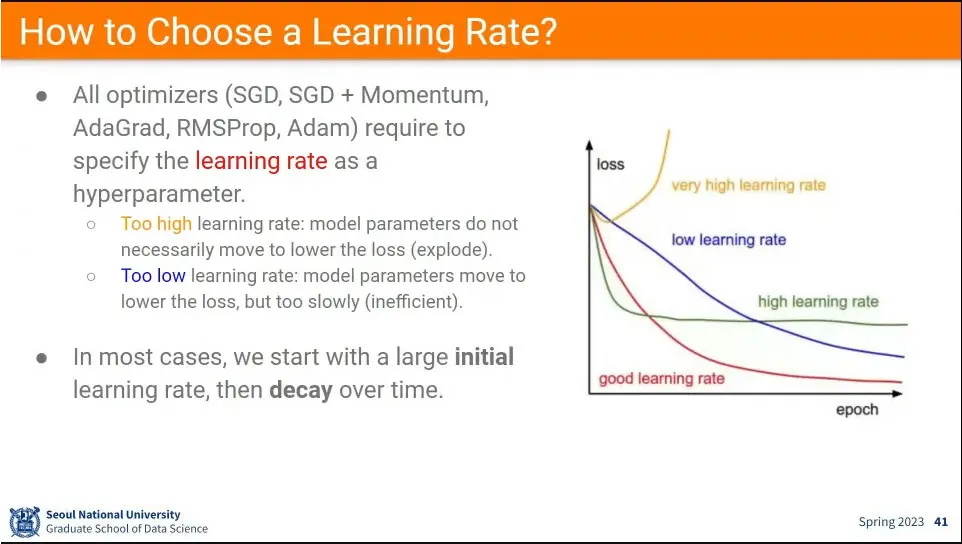
좋은 learning rate를 설정해야 학습이 잘 된다.
•
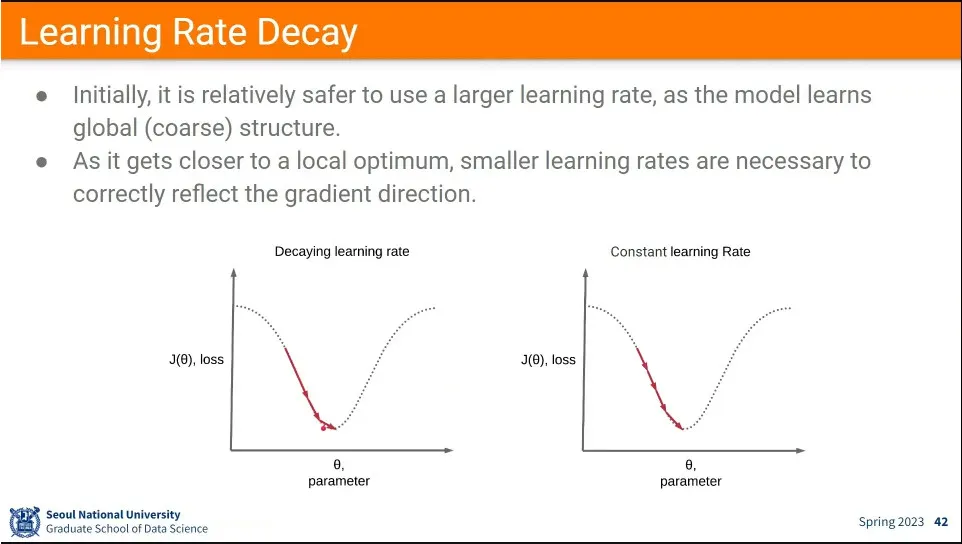
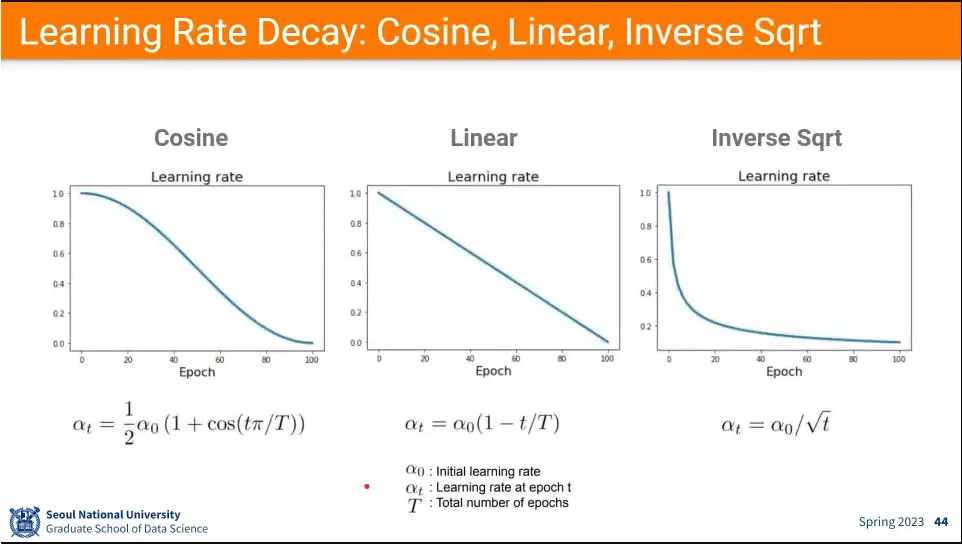
실용적으로는 처음에는 빨리 내려가도록 learning rate를 높게 주고, 뒤로 갈수록 점점 작게 하는 방법을 쓴다. 이것이 learning rate decay라고 함.
•
실제 사례
◦
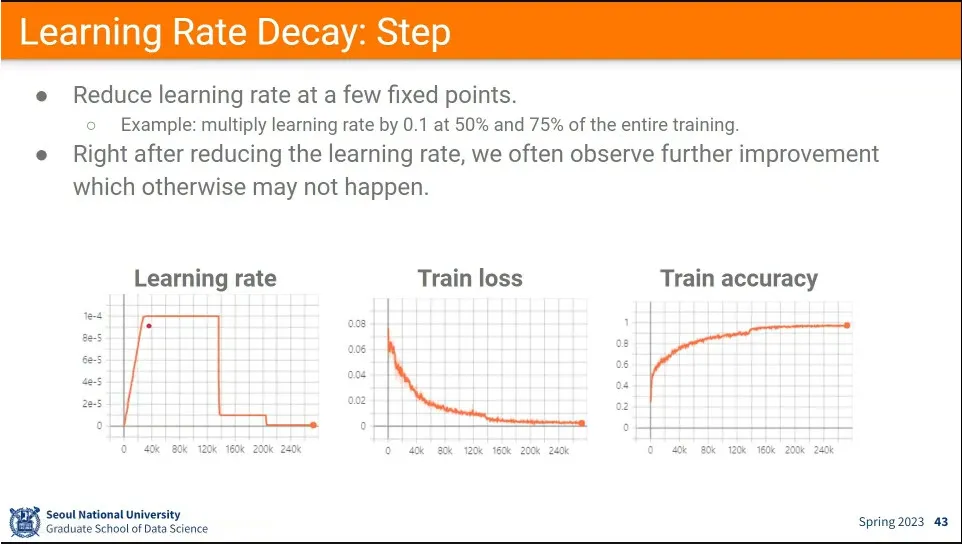
처음에는 learning rate을 0으로 시작해서 높였다가, —이것을 learning rate warm-up이라고 함
◦
그 후에 1/10 씩 줄이면서 학습 함. —이것은 특별한 기준 없이 경험적인 값.
•
learning rate을 줄이는 방법들
•
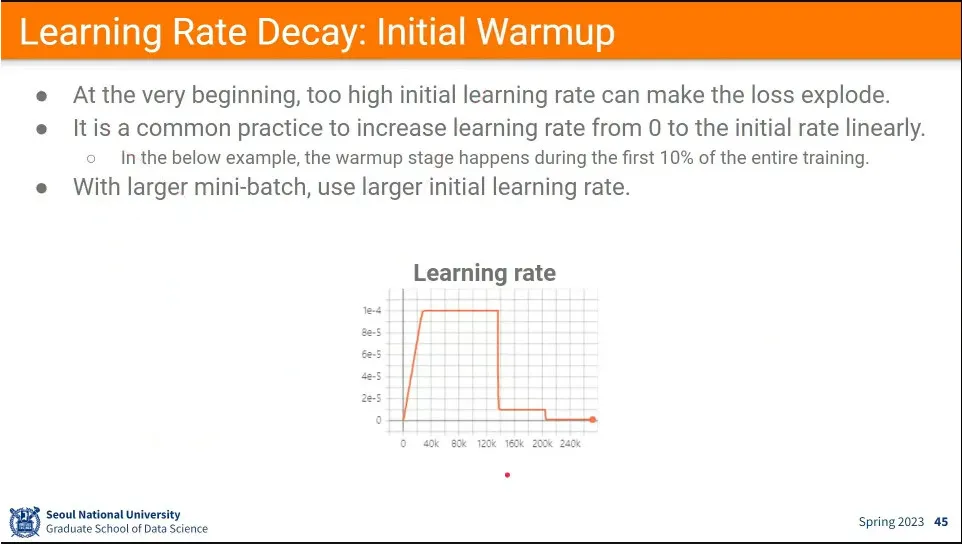
learning rate은 줄이는 방향으로 가는게 일반적이지만, 처음에는 늘려서 학습 시킬 수 있는데, 이것이 initial warmup이라고 함.
◦
목표로 하는 최댓값까지 선형적으로 늘리고, 그 후에 줄임.
•
현업에서는 learning rate을 조절하는게 상당히 중요한 업무이다.