Search
Duplicate

Computer Vision/ 2. Single View Metrology

web.stanford.edu
https://web.stanford.edu/class/cs231a/course_notes/02-single-view-metrology.pdf

1 Introduction

이전 강의 노트에서 현실의 점을 변환하는 방법을 논의했다. 카메라의 extrinsic과 intrinsic 속성을 사용하여 3d 세계를 디지털 이미지로 바꾼다. 우리는 calibration rig의 알려진 구조와 그에 대응하는 이미지를 사용하여 이러한 카메라의 속성을 추론할 수 있는 방법을 살펴보았다. 이 시간에 우리는 관련된 문제를 살핀다. 단일 이미지와 이미지를 촬영한 카메라의 속성이 주어지면 3d 세계의 알려진 구조를 복구할 수 있는가? 그 다음 더 일반적으로 단일 이미지에서 어떤 정보를 추론될 수 있는지를 논의한다.

2 Transformations in 2D

이미지에서 학습하는 방법을 더 잘 이해하려면 우선 2d 공간의 다양한 변형에 관해 알아야 한다.
Isometric transformation은 거리를 보존하는 변환이다. 가장 기본적인 형식에서 isometry는 rotation RR과 translation tt로 설명된다. 따라서 수학적으로 다음처럼 정의된다.
[x′y′1]=[Rt01][xy1]\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix}\begin{bmatrix} x \\ y \\ 1\end{bmatrix}
여기서 [x′y′1]⊤[x' \quad y' \quad 1]^\top는 isometric transformation 후에 달성된 점이다.
Similarity transformation은 shape을 보존하는 변환이다. 직관적으로 isometric transfomation과 scaling이 가능한 모든 작업을 수행할 수 있다. 수학적으로 다음처럼 표기된다.
[x′y′1]=[SRt01][xy1],S=[s00s]\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} SR & t \\ 0 & 1 \end{bmatrix}\begin{bmatrix} x \\ y \\ 1\end{bmatrix}, S = \begin{bmatrix} s & 0 \\ 0 & s\end{bmatrix}
이것이 shape을 보존하므로 그들은 또한 길이와 각도의 비율을 보존한다. 모든 isometric transformation이 s=1s=1인 similarity transformation의 특별한 형식임에 유의하라. 그러나 그 반대는 성립하지 않는다.
Affine transformation은 점, 직선, 평행성을 보존하는 변환이다. 어떤 벡터 vv에 대해 affine transformation TT는 다음과 같이 정의된다.
T(v)=Av+tT(v) = Av + t
여기서 AA는 Rn\mathbb{R}^n의 선형 변환이다. homogeneous 좌표에서 affine transformation은 종종 다음과 같이 작성된다.
[x′y′1]=[At01][xy1]\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} A & t \\ 0 & 1 \end{bmatrix}\begin{bmatrix} x \\ y \\ 1\end{bmatrix}
위의 방정식에서 모든 similarities(그리고 따라서 isometric)이 affinities의 특별한 경우임을 쉽게 볼 수 있다.
Projective transformation 또는 homographies는 line을 line으로 매핑하는 임의의 변환이지만 평행성을 보존할 필요가 없다. homogeneous 좌표계에서 projective transformation은 다음처럼 표현된다.
[x′y′1]=[Atvb][xy1]\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} A & t \\ v & b \end{bmatrix}\begin{bmatrix} x \\ y \\ 1\end{bmatrix}
이 형식이 affine transformation을 더 일반화한 것임을 볼 수 있다. 추가 자유도는 vv를 추가하여 추가된다.
평행성을 보존하지 않음에도 projective transformation은 line을 line으로 매핑하므로 점의 collinearity(동선성)를 보존한다. 게다가 collinear(동선) 상의 4개 점의 교차 비율이 projective transformation 에 대해 불변으로 유지된다. cross ratio는 한 line에서 4개 점 P1,P2,P3,P4P_1, P_2, P_3, P_4을 취하고 다음과 같이 계산한다.
cross ratio=∥P3−P1∥∥P4−P2∥∥P3−P2∥∥P4−P1∥(1)\text{cross ratio} = {\|P_3-P_1\|\|P_4-P_2\| \over \|P_3-P_2\|\|P_4-P_1\|} \tag{1}
우리는 projective transformation 아래 cross ratio의 불변성의 증명을 연습 문제로 남긴다.

3 Points and Lines at Infinity

직선은 이미지에서 구조를 결정하는 것에 대해 중요하다. 따라서 2d와 3d에서 선의 정의를 아는 것이 필수적이다. 2d에서 직선은 homogeneous 벡터 ℓ=[abc]⊤\ell = [a \quad b \quad c]^\top로 표현될 수 있다. 비율 −ab-{a\over b}는 선의 slope(기울기)를 포착하고 비율 −cb-{c\over b}는 yy-intercept(절편)을 포착한다. 형식적으로 2d 직선은 다음처럼 정의된다.
∀p=[xy]∈ℓ,[abc][xy1]=0(2)\forall p = \begin{bmatrix}x \\ y \end{bmatrix} \in \ell, \begin{bmatrix}a & b & c \end{bmatrix}\begin{bmatrix}x \\ y \\ 1 \end{bmatrix} = 0 \tag{2}
일반적으로 두 직선 ℓ\ell과 ℓ′\ell'은 점 xx에서 교차된다. 이 점은 ℓ\ell과 ℓ′\ell' 사이의 cross product로 정의된다.
증명. 두 직선 ℓ\ell과 ℓ′\ell'의 교차가 주어지면 교차점 xx은 두 직선 ℓ\ell과 ℓ′\ell'에 모두 놓인다. 그러므로 x⊤ℓ=0x^\top\ell = 0이고 x⊤ℓ′=0x^\top\ell' = 0이다. 만일 x=ℓ×ℓ′x = \ell\times \ell'을 설정하면 cross product의 정의에 의해 벡터 xx는 두 벡터 ℓ\ell와 ℓ′\ell'에 orthogonal이다. orthogonality의 정의에 의해 x⊤ℓ=0x^\top\ell = 0이고 x⊤ℓ′=0x^\top\ell' = 0이다. 따라서 xx의 정의는 제약을 만족한다.
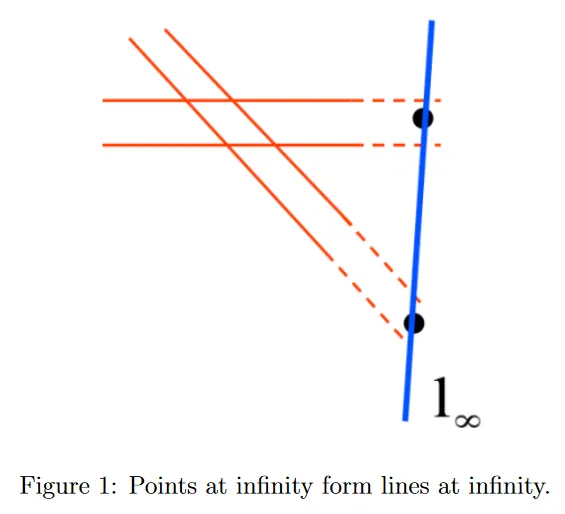
평행선의 경우는 어떠한가? 일상적 지식으로는 이 선들이 절대 교차하지 않는다고 한다. 그러나 이 정의를 평행선이 무한대에서 교차한다고 다시 작성할 수 있다. homogeneous 좌표에서 무한대에서 점은 [xy0]⊤[x \quad y \quad 0]^\top로 작성된다. 유클리드 좌표는 모든 좌표를 마지막 좌표로 나누어 얻는다. 이 경우에 좌표가 0이므로 무한대의 점이 된다. 그러므로 homogeneous 좌표는 평행선의 경우에서도 교차를 정의하는 좋은 형식이다.
이제 두 평행선 ℓ\ell와 ℓ′\ell'을 고려하자. 두 직선이 평행할 때, 그들의 slope는 동등하므로 ab=a′b′{a \over b} = {a' \over b'}이다. homogeneous 좌표를 사용하여 교차점을 계산하면 다음을 확인할 수 있다.
ℓ×ℓ′∝[b−a0]=x∞(3)\ell \times \ell' \propto \begin{bmatrix}b \\ -a \\ 0 \end{bmatrix} = x_\infty \tag{3}
따라서 두 평행선이 무한대에서 교차한다는 우리의 직관을 확인할 수 있다. 두 평행선의 무한대에서의 교차점을 ideal point라고 부른다. 무한대에서 점의 흥미로운 속성 하나는 동일한 slope −ab-{a\over b}를 가진 모든 평행선이 다음과 같이 ideal point를 통과한다는 것이다.
ℓ⊤x∞=[abc][b−a0]=0(4)\ell^\top x_\infty = \begin{bmatrix}a & b & c \end{bmatrix} \begin{bmatrix}b \\ -a \\ 0 \end{bmatrix} = 0 \tag{4}
무한대의 점의 개념을 확장하여 무한대의 선을 정의할 수 있다. 2개 이상의 평행선 쌍을 고려하자. 각 평행선의 쌍은 무한대에서 한 점 {x∞,1,...,x∞,n}\{x_{\infty, 1}, ..., x_{\infty, n}\}에서 교차한다. 이 무한대의 모든 점을 지나는 직선 ℓ∞\ell_\infty는 ∀i,ℓ∞⊤x∞,i=0\forall i, \ell_\infty^\top x_{\infty, i} = 0를 만족해야 한다. 이것은 ℓ∞=[00c]⊤\ell_\infty = [0 \quad 0 \quad c]^\top를 의미한다. cc가 임의의 값이므로 ℓ∞=[001]⊤\ell_\infty = [0 \quad 0 \quad 1]^\top로 단순화할 수 있다.
일반적인 projective transformation HH를 무한대의 점 p∞p_\infty에 적용하면 어떤 일이 발생할까?
p′=Hp∞=[Atvb][110]=[px′py′pz′](5)p' = Hp_\infty = \begin{bmatrix}A & t \\ v & b \end{bmatrix} \begin{bmatrix}1 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} p_x' \\ p_y' \\ p_z' \end{bmatrix} \tag{5}
p′p'의 마지막 요소가 non-zero일 수 있다는 것에 유의하라. 이것은 일반적으로 projective transformation이 무한대의 점을 무한대가 아닌 점에 매핑하는 것을 시사한다. 그러나 affine transformation의 경우 무한대의 점은 무한대의 점에 매핑된다.
p′=Hp∞=[At01][110]=[px′py′0](6)p' = Hp_\infty = \begin{bmatrix}A & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix}1 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} p_x' \\ p_y' \\ 0 \end{bmatrix} \tag{6}
이제 projective transformation HH를 직선 ℓ\ell에 적용하여 새로운 직선 ℓ′\ell'을 얻는다고 하자. 직선을 지나는 모든 점 xx은 x⊤ℓ=0x^\top\ell = 0이라는 속성을 만족해야 한다. 변환된 공간에서 직선이 여전히 직선에 매핑되므로 x′ℓ′=0x'\ell' = 0이다. identify 속성을 사용하여 다음을 얻을 수 있다.
x⊤Iℓ=x⊤H⊤H−⊤ℓ=0x^\top I \ell = x^\top H^\top H^{-\top}\ell = 0
직선에 projective transformation을 적용하면 모든 점도 변환되어 x′=Hxx' = Hx가 된다. 따라서 x⊤H⊤H−⊤ℓ=x′⊤ℓ′x^\top H^\top H^{-\top}\ell = x'^\top\ell'를 얻고 직선의 projective 변환이 ℓ′=H−⊤ℓ\ell' = H^{-\top}\ell임을 알 수 있다. 무한대에서 점에 대한 관찰과 유사하게 무한대에서 직선의 projective transformation은 반드시 무한대에서 다른 직선에 매핑되지 않는다. 게다가 affine transformation은 여전히 무한대의 직선을 무한대에서 직선으로 매핑한다.

4 Vanishing Points and Lines

지금까지 2d에 무한대에서 선과 점의 개념을 소개했다. 이제 3d에 대해 그것에 해당하는 homogeneous 좌표에서 동등한 개념을 소개한다.
이제 3d 세계에서 평면의 개념을 유도한다. 우리는 평면을 벡터 [abcd]⊤[a \quad b \quad c \quad d]^\top로 표현할 수 있다. 여기서 (a,b,c)(a, b, c)는 normal 벡터이고 dd는 normal 벡터의 방향에서 원점에서 평면까지의 거리이다. 형식적으로 평면은 다음을 만족하는 모든 점 xx에 의해 정의된다.
x⊤[abcd]=ax1+bx2+cx3+d=0(7)x^\top \begin{bmatrix}a\\b\\c\\d \end{bmatrix} = ax_1 + bx_2 + cx_3 + d = 0 \tag{7}
3d에서 직선은 두 평면의 교차로 정의된다. 4개의 자유도를 갖기 때문에(정의된 절편 위치와 3차원 각각의 slope), 3d 공간에서 나이스하게 표현하는 것이 어렵다. 더 상세한 내용은 Hartley & Zisserman의 교재의 섹션 3.2.2를 참조하라
그러나 3d에서 점은 2d에서와 유사하게 정의된다. 3d에서 무한대의 점은 다시 3d에서 평행선의 교차점으로 정의된다. 게다가 이러한 무한대의 점 x∞x_\infty에 projective transformation을 적용하면 homogeneous 좌표에서 무한대가 아닌 이미지 평면에서 점 x∞x_\infty을 얻을 수 있다. 이 점 x∞x_\infty를 vanishing point(소실점)이라고 부른다. 그러나 우리는 vanishing point로 무엇을 할 수 있을까?
3d에서 평행선, 이미지 대응 vanishing point, 카메라 파라미터 K,R,TK, R, T 사이의 유용한 관계를 유도할 수 있다. 카메라 reference system에서 3d 평행선의 집합의 방향을 d=(a,b,c)d = (a, b, c)라 정의하자. 이 직선들은 무한대의 한 점에서 교차하고 그 점을 이미지에 projection하면 다음처럼 정의되는 vanishing point vv가 된다.
v=Kd(8)v = Kd \tag{8}
우리는 위의 방정식의 유도를 연습문제로 남긴다. 이 방정식은 방향 dd를 추출하여 재작성할 수 있다.
d=K−1v∥K−1v∥(9)d = {K^{-1} v \over \|K^{-1}v\|} \tag{9}
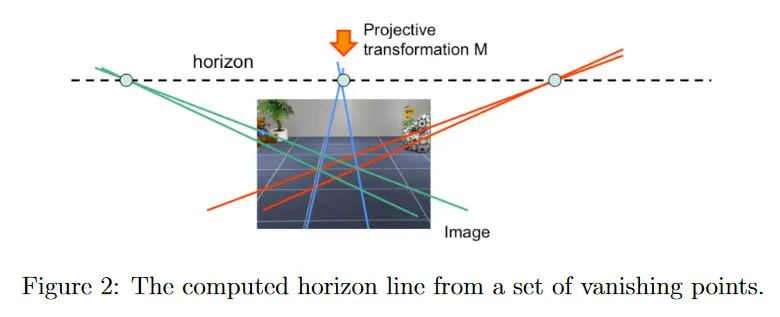
평면 Π\Pi를 평행선의 superset으로 고려하면, 각 평행선의 집합은 무한대에서 한 점에서 교차한다. 이러한 무한대의 점들의 집합을 지나는 직선이 Π\Pi와 연관된 무한대의 선 ℓ∞\ell_\infty이다. 무한대에서 직선은 또한 두 평행 평면이 교차하는 선으로 정의될 수 있다. ℓ∞\ell_\infty를 이미지 평면으로 projective transformation하면 더는 무한대의 선이 아니며, 이를 vanishing line(소실선) 또는 horizon line(수평선) ℓhoriz\ell_\text{horiz}라 부른다. horizon line은 이미지의 대응 vanishing point를 지나는 선이다. horizon line을 다음처럼 계산할 수 있다.
ℓhoriz=HP−⊤ℓ∞(10)\ell_\text{horiz} = H_P^{-\top}\ell_\infty \tag{10}
horizontal line의 개념을 통해 수학적으로 쉽게 드러나지 않는 이미지의 속성을 직관적으로 추론할 수 있다. 예컨대 그림 2는 지면의 선들이 이미지 좌표에서 평행이 아니지만, 우리는 자연스럽게 그 선들이 3d 세계에서 평행하다는 것을 이해할 수 있다.
게다가 horizon line을 통해 세계에 관한 유용한 속성을 계산할 수 있다. 예컨대 우리는 3d에서 평면의 normal nn과 이미지에서 해당하는 horizon line ℓhoriz\ell_\text{horiz} 사이에 흥미로운 관계를 유도할 수 있다.
n=K⊤ℓhoriz(11)n = K^\top \ell_\text{horiz} \tag{11}
이것은 평면과 연관된 horizon line을 인식할 수 있고 카메라가 calibration 되어 있으면 그 평면의 orientation을 추정할 수 있다는 뜻이다.
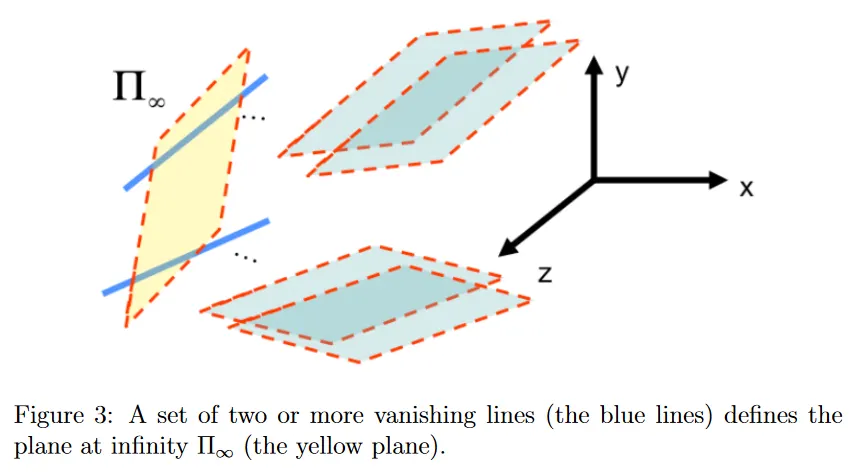
vanishing point와 line과 관련된 마지막 속성을 소개하기 전에 우선 무한대의 평면 Π∞\Pi_\infty를 정의해야 한다. 이 평면은 2개 이상의 vanishing line의 집합으로 정의되며 homogeneous 좌표에서 벡터 [0001]⊤[0 \quad 0 \quad 0 \quad 1]^\top에 의해 설명된다.
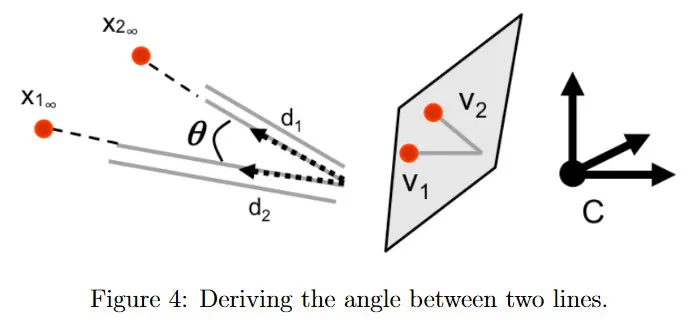
마지막으로 소개할 속성은 3d에서 선과 평면을 이미지 평면에서 대응하는 vanishing point와 선에 연관시킨다. 3d에서 두 쌍의 평행선이 방향 d1d_1과 d2d_2를 가지고 무한대의 점 x1,∞x_{1,\infty}와 x2,∞x_{2,\infty}와 연관되어 있다고 가정하자. 해당하는 vanishing point를 v1v_1와 v2v_2라 하자. 그러면 d1d_1과 d2d_2 사이의 각도 θ\theta는 cosine 규칙을 사용하여 다음과 같이 주어진다.
cos⁡θ=d1⋅d2∥d1∥∥d2∥=v1⊤ωv2v1⊤ωv1v2⊤ωv2(12)\begin{aligned} \cos \theta &= {d_1 \cdot d_2 \over \|d_1\|\|d_2\|}\\ &= {v_1^\top \omega v_2 \over \sqrt{v_1^\top \omega v_1} \sqrt{v_2^\top \omega v_2}} \end{aligned} \tag{12}
여기서 ω=(KK⊤)−1\omega = (KK^\top)^{-1}
우리는 이 아이디어를 3d planar 경우로 더 확장할 수 있다. 여기서 우리는 3d에서 서로 다른 평면을 연관 시키기를 원한다. 임의의 평면에 대해 연관된 vanishing line ℓhoriz\ell_\text{horiz}와 normal K⊤ℓhorizK^\top \ell_\text{horiz}을 계산할 수 있음을 떠올려라. 따라서 각 평면의 normal 벡터 n1n_1과 n2n_2 사이의 각도를 계산하여 두 평면 사이의 각도 θ\theta를 결정할 수 있다. 각각 vanishing line ℓ1\ell_1과 ℓ2\ell_2를 가진 두 평면 사이의 각도 θ\theta는 다음과 같이 유도할 수 있다.
cos⁡θ=n1⋅n2∥n1∥∥n2∥=ℓ1⊤ω−1ℓ2ℓ1⊤ω−1ℓ1ℓ2⊤ω−1ℓ2(13)\begin{aligned} \cos \theta &= {n_1 \cdot n_2 \over \|n_1\|\|n_2\|}\\ &= {\ell_1^\top \omega^{-1}\ell_2 \over \sqrt{\ell_1^\top \omega^{-1} \ell_1} \sqrt{\ell_2^\top \omega^{-1} \ell_2}} \end{aligned} \tag{13}

5 A Single View Metrology Example

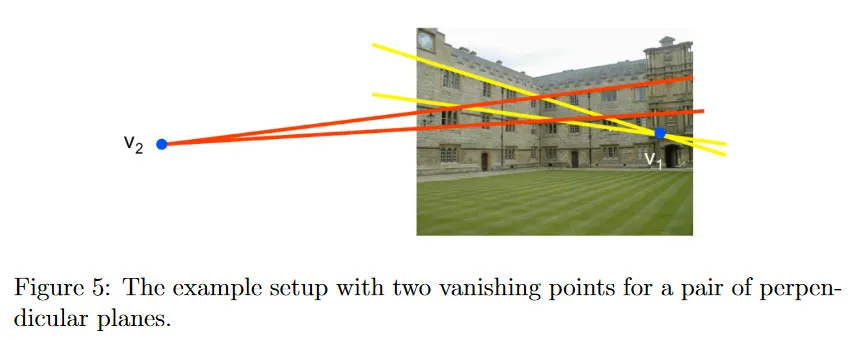
3d 세계에서 이미지의 두 평면을 식별할 수 있다고 가정하자. 추가로 이 평면 각각에서 평행선 쌍을 식별할 수 있다고 하자. 이것은 이미지에서 두 vanishing point v1v_1과 v2v_2를 추정하는 것이다. 마지막으로 이러한 평면이 3d에서 서로 perpendicular(수직)임을 알고 있다고 가정하자. 이 경우에 방정식 12에 따라 v1ωv2=0v_1\omega v_2 = 0임을 알 수 있다.
그러나 ω\omega가 현재 알려지지 않은 카메라 행렬 KK에 의존한다는 것을 떠올려라. 그러므로 이 두 vanishing point만으로 카메라 파라미터를 정확하게 추정할 수 있는가? KK가 5개의 자유도를 가지고 v1ωv2=0v_1\omega v_2 = 0가 단 하나의 제약조건만 제공하는 것을 고려하므로 KK를 계산하기 위한 충분한 정보가 없다.
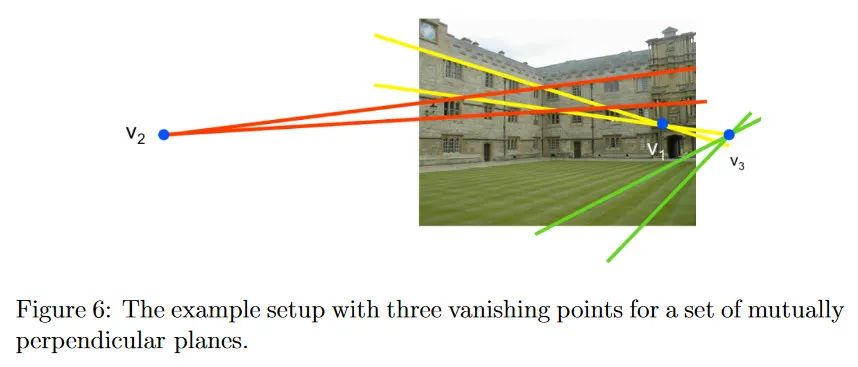
서로 orthogonal인 또 다른 평면에 대한 또 다른 vanishing v3v_3을 찾을 수 있다면 어떠한가? 그러면 v1ωv2=v1ωv3=v2ωv3=0v_1\omega v_2 = v_1\omega v_3 = v_2\omega v_3 = 0임을 알 수 있다. 각 쌍이 제약조건을 하나씩 제공하므로 KK를 계산하는데 5개의 제약 조건 중 3개만 얻게 된다. 그러나 카메라가 zero-skew이고 square pixel이라고 가정하면 필요한 추가적인 2개 제약조건을 추가할 수 있다. 이러한 가정하에 ω\omega는 다음 형식을 취한다.
ω=[ω10ω40ω1ω5ω4ω5ω6](14)\omega = \begin{bmatrix} \omega_1 & 0 & \omega_4 \\ 0 & \omega_1 & \omega_5 \\ \omega_4 & \omega_5 & \omega_6 \end{bmatrix} \tag{14}
주의 깊게 보았다면 ω\omega의 정의에서 4개 변수가 존재하는 것을 알 수 있다. 그러나 ω\omega를 scale까지만 알 수 있으므로 실제 변수의 양을 3개로 축소하여 해를 구할 수 있다. ω\omega를 구했다면 Cholesky decomposition을 사용하여 KK를 계산할 수 있다. 따라서 단일 이미지만으로 카메라를 calibrate 할 수 있다.
KK가 알려지면 장면의 3d 지오메트리를 재구축할 수 있다. 예컨대 위에서 식별된 모든 평면의 orientation을 계산할 수 있다. 그러므로 단일 이미지만으로도 촬영된 장면에 관한 풍부한 정보를 readily(손쉽게) 얻을 수 있다.
Made with