Search
Duplicate

AI/ Stochastic Differential Equation(SDE), Ordinary Differential Equation(ODE)

SDE와 ODE는 DDPM과 달리 노이즈를 추가하고 제거하는 방식이 아니라 시스템의 변화를 모델링하는 drift와 diffusion을 이용하여 샘플을 생성하는 방법이다.

Stochastic Differential Equation(SDE)

Stochastic Differential Equation (SDE)는 미분 방정식의 한 형태로 불확실성이나 랜덤한 변동을 모델링하기 위해 확률 과정을 포함한다. SDE는 다음과 같이 작성할 수 있다.
dx=f(x,t)⏟driftdt+g(t)⏟diffusiondwd\bold{x} = \underbrace{\bold{f}(\bold{x},t)}_{\text{drift}}dt + \underbrace{g(t)}_{\text{diffusion}} d\bold{w}
첫 번째 항은 drift coefficient라 하고 시스템의 결정론적 변화를 나타낸다. 두 번째 항은 diffusion coefficient라 하고 불확실성이나 노이즈의 영향을 모델링한다. dwd\bold{w}는 표준 브라운 운동(또는 Wiener Process)를 나타내며 가우시안 화이트 노이즈의 통합된 형태이다.
SDE는 DDPM과 같이 모델이 노이즈를 예측하고 그 결과를 실제 노이즈와 비교하여 학습한다.

Forward Diffusion SDE

diffusion 절차를 다음과 같이 고려한다. 여기서 노이즈 레벨 βt\beta_t는 β(t)Δt\beta(t)\Delta t로 재작성되고 Δt\Delta t는 step size이다.
xt=1−βtxt−1+βtN(0,I)=1−β(t)Δtxt−1+β(t)ΔtN(0,I)\begin{aligned} \bold{x}_t &= \sqrt{1-\beta_t}\bold{x}_{t-1} + \sqrt{\beta_t}\mathcal{N}(\bold{0},\bold{I}) \\&= \sqrt{1-\beta(t)\Delta t}\bold{x}_{t-1} + \sqrt{\beta(t) \Delta t}\mathcal{N}(\bold{0},\bold{I}) \end{aligned}
Δt\Delta t가 작으면 1차 테일러 급수 전개를 사용하여 첫 번째 항을 근사하여 다음을 얻을 수 있다.
xt≈xt−1−β(t)Δt2xt−1+β(t)ΔtN(0,I)\bold{x}_t \approx \bold{x}_{t-1} - {\beta(t) \Delta t \over 2}\bold{x}_{t-1} + \sqrt{\beta(t) \Delta t}\mathcal{N}(\bold{0},\bold{I})
따라서 작은 Δt\Delta t에 대해 다음을 갖는다.
xt−xt−1Δt≈−β(t)2xt−1+β(t)ΔtN(0,I){\bold{x}_t - \bold{x}_{t-1} \over \Delta t} \approx -{\beta(t) \over 2} \bold{x}_{t-1} + {\sqrt{\beta(t)} \over \sqrt{\Delta t}}\mathcal{N}(\bold{0},\bold{I})
이제 연속 시간 한계로 전환하고 이것을 다음의 stochastic differential equation(SDE)로 작성한다.
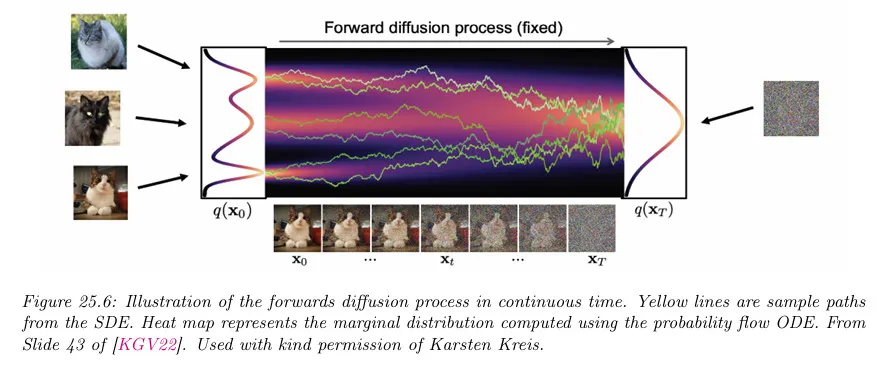
dx(t)dt=12β(t)x(t)+β(t)dw(t)dt{d\bold{x}(t) \over dt} = {1\over2} \beta(t)\bold{x}(t) + \sqrt{\beta(t)} {d\bold{w}(t) \over dt}
이 절차에 대한 1차원 예는 아래 그림 참조. 왼쪽의 t=0t=0에서 데이터 분포가 점차 오른쪽의 t=1t=1에서의 순수 노이즈 분포로 변환되는 것을 볼 수 있다.
데이터 분포에서 초기 상태를 샘플링하고 시간이 지남에 따라 다음과 같은 Euler-Maruyama 적분을 사용하여 다음과 같이 적분한다. (Euler-Maruyama 방법은 SDE를 이산화하여 수치적으로 근사하는 방법이다.)
x(t+Δt)=x(t)+f(x(t),t)Δt+g(t)ΔtN(0,I)\bold{x}(t + \Delta t) = \bold{x}(t) + \bold{f}(\bold{x}(t),t)\Delta t + g(t) \sqrt{\Delta t}\mathcal{N}(\bold{0},\bold{I})
T→∞T \to \infty 극한에서 DDPM에 해당하는 SDE가 다음처럼 주어지는 것을 보일 수 있다. 여기서 β(t/T)=Tβt\beta(t/T) = T\beta_t
dx=−12β(t)xdt+β(t)dωd\bold{x} = -{1\over2} \beta(t)\bold{x} dt+\sqrt{\beta(t)}d\boldsymbol{\omega}
여기서 drift 항은 −x-\bold{x}에 비례하며 이것은 프로세스가 0으로 돌아가는 것을 장려한다. 결론적으로 DDPM은 variance preserving process에 해당한다.
반면에 Score-based Generation Model에 해당하는 SDE는 다음처럼 주어진다. 여기서 σ(t/T)=σt\sigma(t/T) = \sigma_t
dx=d[σ(t)2]dtdωd\bold{x} = \sqrt{d[\sigma(t)^2] \over dt}d\boldsymbol{\omega}
이 SDE는 0 drift를 가지므로 variance exploding process에 해당한다.

Reverse Diffusion SDE

모델에서 샘플을 생성하려면 SDE를 역전시킬 수 있어야 한다. 놀랍게도 dx=f(x,t)dt+g(t)dwd\bold{x} = \bold{f}(\bold{x},t)dt + g(t) d\bold{w} 형식의 forward SDE를 역전 시켜서 다음의 reverse-time SDE를 얻을 수 있다.
dx=[f(x,t)−g(t)2∇xlog⁡qt(x)]dt+g(t)dwˉd\bold{x} = [f(\bold{x},t)-g(t)^2\nabla_\bold{x} \log q_t(\bold{x})] dt + g(t) d\bar{\bold{w}}
여기서 wˉ\bar{\bold{w}}는 시간 흐름이 역방향일 때 표준 Wiener 절차이고, dtdt는 극소의 음의 시간 단계이고 ∇xlog⁡qt(x)\nabla_\bold{x} \log q_t(\bold{x})는 score 함수이다.
DDPM의 경우에 reverse SDE는 다음 형식을 갖는다.
dxt=[−12β(t)xt−β(t)∇xtlog⁡qt(xt)]dt+β(t)dwˉtd\bold{x}_t = \left[-{1\over2}\beta(t)\bold{x}_t - \beta(t)\nabla_{\bold{x}_t} \log q_t(\bold{x}_t) \right] dt + \sqrt{\beta(t)}d\bar{\bold{w}}_t
denoising score matching을 사용하여 다음을 얻을 수 있다.
∇xtlog⁡qt(xt)≈sθ(xt,t)\nabla_{\bold{x}_t} \log q_t(\bold{x}_t) \approx \bold{s}_{\boldsymbol{\theta}}(\bold{x}_t,t)
이 경우 SDE는 다음이 된다.
dxt=−12β(t)[xt+2sθ(xt,t)]dt+β(t)dwˉtd\bold{x}_t = -{1\over2}\beta(t)[\bold{x}_t + 2\bold{s}_{\boldsymbol{\theta}}(\bold{x}_t,t)] dt + \sqrt{\beta(t)}d\bar{\bold{w}}_t
score 네트워크를 맞춘 후에 ancestral sampling를 사용하여 샘플링 하거나 Euler-Maruyama 적분 스키마를 사용하여 다음과 같은 결과를 얻을 수 있다.
xt−1=xt+12β(t)[xt+2sθ(xt,t)]Δt+β(t)ΔtN(0,I)\bold{x}_{t-1} = \bold{x}_t + {1\over2} \beta(t)[\bold{x}_t+2\bold{s}_{\boldsymbol{\theta}}(\bold{x}_t,t)]\Delta t + \sqrt{\beta(t)\Delta t}\mathcal{N}(\bold{0},\bold{I})

Sample Code

SDE는 drift와 diffusion을 이용해 샘플을 생성한다는 점을 제외하면 DDPM과 유사하다. forward와 reverse의 샘플을 생성하는 부분을 제외하면 나머지는 DDPM의 구현을 그대로 사용할 수 있다.
SDE의 이론에 따라 forward 단계의 샘플을 생성하는 함수는 아래처럼 구현된다.
dx=−12β(t)xdt+β(t)dωd\bold{x} = -{1\over2} \beta(t)\bold{x} dt+\sqrt{\beta(t)}d\boldsymbol{\omega}
# sde 버전의 q_sample() def sde_q_sample(x_start, beta_schedule, dt, num_steps, device): """ Simulate the forward SDE using Euler-Maruyama method. """ x = x_start for i in range(num_steps): beta_t = beta_schedule[i] drift = -0.5 * beta_t * x * dt diffusion = torch.sqrt(beta_t * dt) * torch.randn_like(x, device=device) x = x + drift + diffusion # 기존 샘플에 dx를 더해서 업데이트 한다. return x
Python
복사
reverse 단계의 샘플을 생성하는 함수는 모델이 예측한 노이즈를 이용하여 아래처럼 구현된다.
dxt=−12β(t)[xt+2sθ(xt,t)]dt+β(t)dwˉtd\bold{x}_t = -{1\over2}\beta(t)[\bold{x}_t + 2\bold{s}_{\boldsymbol{\theta}}(\bold{x}_t,t)] dt + \sqrt{\beta(t)}d\bar{\bold{w}}_t
# sde 버전의 p_sample() def sde_p_sample(model, x, beta_schedule, dt, num_steps, device): """ Simulate the reverse SDE using learned noise estimation. """ for i in reversed(range(num_steps)): beta_t = beta_schedule[i] predicted_noise = model(x, torch.tensor([i], device=device)) # Model predicts noise reverse_drift = -0.5 * beta_t * (x - 2 * predicted_noise) * dt reverse_diffusion = torch.sqrt(beta_t * dt) * torch.randn_like(x, device=device) x = x + reverse_drift + reverse_diffusion return x
Python
복사
SDE에서 학습은 DDPM과 마찬가지로 모델이 예측한 noise와 실제 noise 사이의 차이를 이용한다.
x_noisy = sde_q_sample(x_real, beta_schedule, dt, num_steps, device) predicted_noise = model(x_noisy, current_time_step) loss = loss_function(predicted_noise, true_noise) # Define appropriate loss function loss.backward() optimizer.step()
Python
복사

Ordinary Differential Equation(ODE)

우선 미분 방정식은 함수와 해당 함수의 도함수들이 포함된 방정식을 의미한다. 일반 방정식은 변수들 사이의 정적인 관계만 나타낼 수 있지만, 미분 방정식은 변수가 다른 변수에 대해 갖는 변화율을 고려할 수 있기 때문에, 동적인 시스템을 나타낼 수 있다.
그 중에서 상미분 방정식(Ordinary Differential Equation, ODE)는 독립 변수가 1개인 —해당 독립 변수에 종속인 변수는 무관— 미분 방정식을 의미한다. 즉 다음과 같은 형식의 방정식이다. (여기서 x(n)x^{(n)}은 xx에 대한 nn차 도함수를 의미한다)
f(x)=anx(n)+an−1x(n−1)+⋯+a1x(1)+a0xf(x) = a_n x^{(n)} + a_{n-1} x^{(n-1)} + \dots + a_1 x^{(1)} + a_0 x
한편 독립 변수를 2개 이상 포함하는 함수를 각각의 변수로 편미분하는 방정식을 편미분 방정식(Partial Differential Equation, PDE)라고 부른다. 즉, 다음과 같은 형태의 방정식이다. 이것은 여러 독립 변수를 갖는 함수를 미분하는 것이 각 독립변수에 대해 편미분한 후 합치는 것으로 정의 되기 때문이다.
f(x,y)=an∂nf∂xn+an−1∂n−1f∂xn−1+⋯+bn∂nf∂yn+bn−1∂n−1f∂yn−1+…f(x, y) = a_n \frac{\partial^n f}{\partial x^n} + a_{n-1} \frac{\partial^{n-1} f}{\partial x^{n-1}} + \dots + b_n \frac{\partial^n f}{\partial y^n} + b_{n-1} \frac{\partial^{n-1} f}{\partial y^{n-1}} + \dots
이에 따르면 상미분 방정식(ODE)는 독립변수가 1개인 편미분 방정식(PDE)로 생각할 수 있다. 유사하게 전미분 방정식 같은 것도 정의할 수 있다.
참고로 적분에 대해서도 유사하게 적분 방정식을 구성할 수 있으며 이것은 경계값 문제나 inverse 문제 등의 시스템의 누적 효과를 계산하는데 사용된다. 국소적인 변화를 다루는 미분 방정식에 비해 적분 방정식은 전역적인 계산을 필요로 하므로 계산 비용이 훨씬 크다.
또한 미분 방정식은 독립변수를 기준으로 상미분/편미분으로 구분하는 것 외에 선형/비선형으로도 구분할 수 있다.
ODE를 이용한 방식은 결정론적이기 때문에 모델을 학습한 후에 원하는 시점 tt에 대한 샘플을 Markov Chain을 따르지 않고 계산을 통해 생성할 수 있다.
ODE는 SDE와 달리 노이즈 항이 없기 때문에 DDPM처럼 모델이 노이즈를 예측하고 그 결과를 실제 노이즈와 비교하여 학습할 수 없다. 대신 모델이 score를 예측하도록 학습되고 해당 score를 데이터셋에서 계산한 실제 score와 비교하여 학습된다. 모델 구조는 DDPM과 동일하지만 모델이 noise가 아니라 score를 예측한다.

Forward Diffusion ODE

매 단계에서 가우시안 노이즈를 추가하는 대신 초기 상태를 샘플하고 다음 형식의 ordinary differential equation(ODE)를 따라 시간에 걸쳐 결정론적으로 진화화도록 할 수 있다.
dx=[f(x,t)−12g(t)2∇xlog⁡pt(x)]⏟h(x,t)dtd\bold{x} = \underbrace{\left[ f(\bold{x},t) -{1\over2}g(t)^2 \nabla_\bold{x} \log p_t(\bold{x})\right]}_{h(\bold{x},t)}dt
위 식에서 f(x,t)f(\bold{x},t)는 시스템의 drift로 결정론적 변화를 나타내고 g(t)g(t)는 diffusion을 나타내고 pt(x)p_t(\bold{x})는 확률함수를 나타낸다. 위 식에서 x\bold{x}는 tt의 종속 변수이고 diffusion은 tt에 의해 확률함수는 x\bold{x}에 의해 결정되므로 결국 전체 식 h(x,t)h(\bold{x},t)는 tt에 의한 결정론적 함수가 된다. 반면 SDE에서는 tt나 x\bold{x}에 의존하지 않는 노이즈 dwd\bold{w}가 diffusion에 곱해지기 때문에 전체 함수가 확률론적이 된다.
이것을 Probability Flow ODE(PF ODE)라고 부른다.
전체 함수가 결정론적이므로 임의의 ODE 솔버를 사용하여 어느 시점의 상태도 계산할 수 있다.
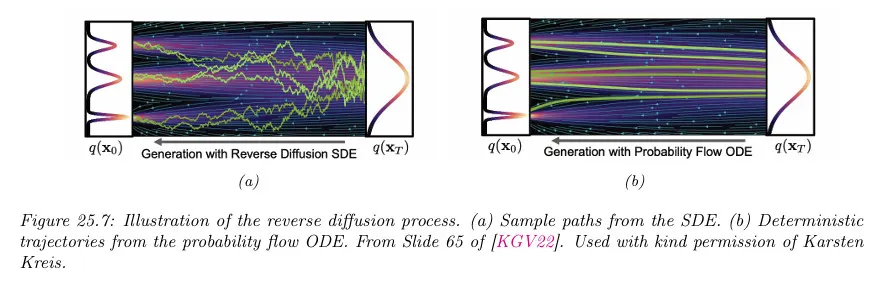
x(t)=x(0)+∫0th(x,τ)dτ\bold{x}(t) = \bold{x}(0) + \int_0^t h(\bold{x},\tau)d\tau
샘플 궤적의 시각화에 대해 아래 그림 참조. 서로 다른 랜덤 상태 x(0)\bold{x}(0)에서 솔버를 시작하면 경로에 대해 유도된 분포는 SDE 모델과 동일한 marginal을 갖는다.
(서로 다른 확률 분포가 동일한 marginal을 가지면 해당 분포들이 특정 변수에 대해 동일한 분포를 나타낸다는 뜻이고, 이것은 그 변수의 확률적 거동이 두 분포에서 동일하다는 의미이다. 다시 말해 SDE와 ODE가 동일한 marginal을 갖는다는 의미는 두 분포가 동일한 확률 분포로 수렴한다는 의미이다.)

Reverse Diffusion ODE

Forward Diffusion ODE에서 한 것과 유사하게 Reverse Time SDE에서 Probability Flow ODE(PF ODE)를 유도하여 다음을 얻을 수 있다.
dxt=[f(x,t)−12g(t)2sθ(xt,t)]dtd\bold{x}_t = \left[f(\bold{x},t)-{1\over2}g(t)^2\bold{s}_{\boldsymbol{\theta}}(\bold{x}_t,t) \right] dt
DDPM에서와 같이 f(x,t)=−12β(t)f(\bold{x},t) = -{1\over2} \beta(t)와 g(t)=β(t)g(t) = \sqrt{\beta(t)}를 설정하면 다음이 된다.
dxt=−12β(t)[xt+sθ(xt,t)]dtd\bold{x}_t = -{1\over2}\beta(t)[\bold{x}_t+\bold{s}_{\boldsymbol{\theta}}(\bold{x}_t,t)] dt
이 ODE를 해결하는 간단한 방법은 Euler’s 방법을 사용하는 것이다.
xt−1=xt+12β(t)[xt+sθ(xt,t)]Δt\bold{x}_{t-1} = \bold{x}_t + {1\over2}\beta(t) [\bold{x}_t + \bold{s}_{\boldsymbol{\theta}}(\bold{x}_t,t)]\Delta t
그러나 실제에서 Heun’s method 같은 고차 ODE 솔버를 사용하면 더 나은 결과를 얻을 수 있다.
이 방법은 continuous normalizing flow이라 부르는 neural ODE의 특별한 경우이다. 결론적으로 정확한 log marginal likelihood를 유도할 수 있다. 그러나 이것을 직접적으로 최대화하는 대신(이것은 비싸다) score matching을 사용하여 모델을 맞춘다.
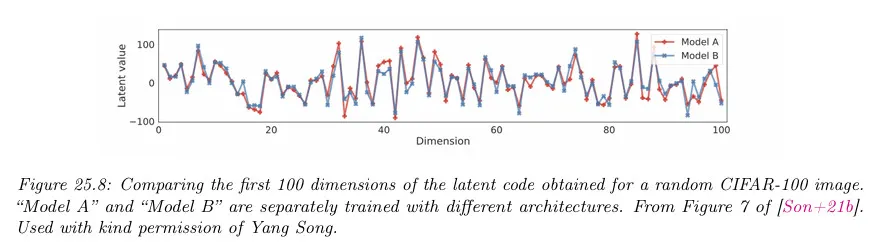
결정론적 ODE 접근의 또 다른 이점은 생성 모델의 식별이 가능하다는 것이다. 이것을 보기 위해 ODE(forward와 reverse 방향 모두)가 결정론적이고 score 함수에 의해 고유하게 결정된다는 것에 유의하라. 아키텍쳐가 충분히 유연하고 충분한 데이터가 있으면 score matching은 데이터 생성 절차의 실제 score 함수를 복구한다. 따라서 학습 후에 주어진 데이터포인트는 모델 아키텍쳐나 초기화에 관계없이 잠재 공간의 고유한 점에 매핑된다. 아래 그림 참조.
게다가 잠재 공간의 모든 점이 고유한 이미지로 디코딩 되므로 잠재 공간에서 ‘의미론적 보간’을 수행하여 두 입력 사이의 속성을 가진 이미지를 생성할 수 있다.

Sample Code

ODE에는 noise가 없기 때문에 모델이 noise를 예측하도록 학습 할 수 없고 대신 score 함수를 예측하도록 학습된다.
ODE는 SDE의 노이즈 부분이 없어진 형태이기 때문에 forward의 샘플은 SDE의 forward에서 diffusion 부분을 없애서 구현할 수 있다.
# ode 버전의 q_sample() def ode_q_sample(x_start, beta_schedule, dt, num_steps): """ Simulate the ODE forward process. """ x = x_start for i in range(num_steps): beta_t = beta_schedule[i] drift = -0.5 * beta_t * x * dt x = x + drift return x
Python
복사
reverse 단계의 샘플을 생성하는 함수는 모델이 예측한 노이즈를 이용하여 아래처럼 구현된다.
xt−1=xt+12β(t)[xt+sθ(xt,t)]Δt\bold{x}_{t-1} = \bold{x}_t + {1\over2}\beta(t) [\bold{x}_t + \bold{s}_{\boldsymbol{\theta}}(\bold{x}_t,t)]\Delta t
# ode 버전의 p_sample() def ode_p_sample(model, x, beta_schedule, dt, num_steps): """ Simulate the ODE reverse process using learned dynamics. """ for i in reversed(range(num_steps)): beta_t = beta_schedule[i] predict_score = model(x, torch.tensor([i])) # Model predicts the dynamics reverse_drift = 0.5 * beta_t * (x + predict_score) * dt x = x + reverse_drift return x
Python
복사
ODE에서 학습은 모델이 예측한 score와 실제 score 사이의 차이를 이용한다. 여기서 실제 score는 데이터셋을 통해 계산된다.
x_noisy = ode_q_sample(x_start, beta_schedule, dt, num_steps) predict_score = model(x_noisy, current_time_step) loss = loss_function(predict_score, true_score) # Define appropriate loss function loss.backward() optimizer.step()
Python
복사

Comparison of the SDE and ODE approach

reverse diffusion SDE를 다음과 같이 재작성하면 SDE와 ODE 사이의 연결을 볼 수 있다.
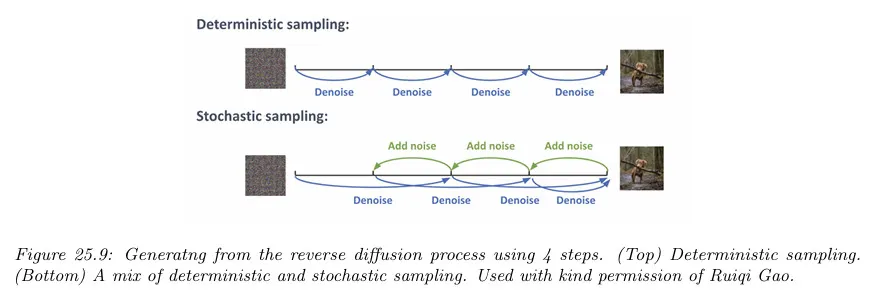
dxt=−12β(t)[xt+sθ(xt,t)]dt⏟probability flow ODE−12β(t)sθ(xt,t)dt+β(t)dwˉt⏟Langevin diffusion SDEd\bold{x}_t = \underbrace{-{1\over2}\beta(t)[\bold{x}_t + \bold{s}_{\boldsymbol{\theta}}(\bold{x}_t,t)] dt}_{\text{probability flow ODE}} \underbrace{-{1\over2}\beta(t)\bold{s}_{\boldsymbol{\theta}}(\bold{x}_t,t)dt + \sqrt{\beta(t)}d\bar{\bold{w}}_t}_{\text{Langevin diffusion SDE}}
연속 노이즈 주입은 ODE 항의 수치적 적분에 의해 도입된 에러에 대해 보상을 줄 수 있고 결과적으로 결과 샘플은 종종 더 좋아 보인다. 그러나 ODE 접근이 더 빠르다.
다행히 이 기법을 결합하는 것이 가능하다. 기본 아이디어는 아래 그림 참조. ODE 솔버를 사용하여 결정론적 단계를 수행한 다음 결과에 작은 양의 노이즈를 추가한다. 이것은 몇 단계 동안 반복될 수 있다.

참고

Made with