Search
Duplicate

AI/ Generative Adversarial Network(GAN)

Implicit Probabilistic Model

VAEs, Normalizing Flowss, Energy-Based Models, Diffusion Models(또는 Score-Based Generative Models) 등과 같이 명시적인 likelihood를 사용하지 않는 likelihood-free 생성 모델을 implicit probabilistic model이라 한다.
이러한 모델은 VAE와 유사하게 확률적 잠재 변수 모델로 표현될 수 있다. 암시적 생성 모델은 파라미터 θ\boldsymbol{\theta}를 사용하여 Rm→Rd\mathbb{R}^m \to \mathbb{R}^d를 매핑하는 결정론적 함수 GθG_{\boldsymbol{\theta}}를 사용하고 잠재 변수 z\bold{z}를 변환한다. 암시적 생성 모델은 likelihood 함수나 관찰 모델을 포함하지 않는다. 대신 생성 절차는 효과적인 likelihood 함수를 형성하는 출력 공간에 유효한 밀도를 정의한다.
x=Gθ(z′)z′∼q(z)qθ(x)=∂∂x1...∂∂xd∫{Gθ(z)≤x}q(z)dz\begin{aligned} \bold{x} &= G_{\boldsymbol{\theta}}(\bold{z}') \\ \bold{z}' &\sim q(\bold{z}) \\ q_\theta(\bold{x}) &= {\partial\over \partial x_1}...{\partial \over \partial x_d}\int_{\{G_{\boldsymbol{\theta}}(\bold{z}) \le \bold{x}\}} q(\bold{z})d\bold{z} \end{aligned}
여기서 q(z)q(\bold{z})는 잠재 변수에 대한 분포로 무작위성의 외부 소스를 제공한다. 마지막 줄은 누적 분포 함수(cdf)의 도함수로 정의된 변환된 밀도 qθ(x)q_\theta(\bold{x})의 정의이고, 집합 {Gθ(z)≤x}\{G_{\boldsymbol{\theta}}(\bold{z}) \le \bold{x}\}에 의해 정의된 모든 사건에 대한 분포 q(z)q(\bold{z})를 적분한다. 잠재와 데이터 차원이 동등하고 (m=d)(m=d) 함수 Gθ(z)G_{\boldsymbol{\theta}}(\bold{z})가 가역이거나 쉽게 특성화되는 근를 가질 때, 확률 분포의 변환에 대한 규칙을 복구한다. 이러한 변수 속성의 변환은 normalizing flow에도 사용될 수 있다. diffusion model에서 데이터로 노이즈를 변환하거나 그 역도 가능하지만 변환은 엄격하게 가역이 아니다.
더 일반적이고 유연한 암시적 생성 모델을 개발할 수 있다. 여기서 함수 GG는 d>md > m인(예: deep network에 의해 지정된) 비선형 함수이다. 이런 모델은 때때로 generator network 또는 generative neural sampler라고 부른다. 또한 differentiable simulator로 생각할 수도 있다. 불행히 이런 모델의 종류에서 위 식의 적분이 까다롭고 집합 {Gθ(z)≤x}\{G_{\boldsymbol{\theta}}(\bold{z}) \le \bold{x}\}을 결정하는 것도 가능하지 않을 수 있다. 물론 까다로움은 VAE과 같은 명시적 잠재 변수 모델의 경우에도 문제가 되지만 GAN의 경우에 likelihood 항의 부재가 학습 문제를 더 어렵게 만든다. 이 문제를 likelihood-free inference 또는 simulation-based inference라고 부른다.
Likelihood-free 추론은 또한 Approximate Bayesian Computation(ABC)로 알려진 영역의 기저를 형성한다. ABC와 GAN은 암시적 생성 모델에서 학습하는 것에 대한 2가지 다른 알고리즘 프레임워크를 제공한다. 두 접근 모두 comparing real and simulated data(실제 데이이터와 시뮬레이션된 데이터를 비교하는)에 기반한 학습 원칙에 기반한다. 이러한 유형의 비교 학습은 likelihood-free 추론의 핵심 원칙을 예시한다.

Generative Adversarial Network(GAN)

•
Note) GAN 목적 함수 유도에 대한 자세한 내용은 AI/ GAN Objective 참조
암시적 생성 모델의 많은 목적들이 min-max 공식을 통해 zero-sum loss을 사용한다. 생성기의 목표는 판별기는 최대화하는 동일한 함수를 최소화하는 것이다. 이것을 다음처럼 형식화할 수 있다.
min⁡max⁡V(ϕ,θ)\min \max V(\boldsymbol{\phi}, \boldsymbol{\theta})
이에 대해 베르누이 log-loss를 사용하면 원래의 GAN을 복구할 수 있다.
V(ϕ,θ)=12Ep∗(x)[log⁡Dϕ(x)]+12Eqθ(x)[log⁡(1−Dϕ(x))]V(\boldsymbol{\phi},\boldsymbol{\theta}) = {1\over2}\mathbb{E}_{p^*(\bold{x})}[\log D_{\boldsymbol{\phi}}(\bold{x})] + {1\over2} \mathbb{E}_{q_\theta(\bold{x})}[\log(1-D_{\boldsymbol{\phi}}(\bold{x}))]
대부분의 학습 원리가 zero-sum 손실로 이어지는 이유는 기본 구조 때문이다. 그러나 반드시 그럴 필요는 없다. LS-GAN의 공식, hinge loss를 사용하여 학습된 GAN, RelativisticGANs과 같은 zero-sum이 아닌 다른 GAN 손실이 존재한다. 따라서 GAN 공식을 다음과 같이 일반화할 수 있다.
min⁡ϕLD(ϕ,θ)max⁡ϕLG(ϕ,θ)\min_{\boldsymbol{\phi}} L_D(\boldsymbol{\phi}, \boldsymbol{\theta})\\\max_{\boldsymbol{\phi}} L_G(\boldsymbol{\phi}, \boldsymbol{\theta})
여기서 −LD(ϕ,θ)=LG(ϕ,θ)=V(ϕ,θ)-L_D(\boldsymbol{\phi},\boldsymbol{\theta}) = L_G(\boldsymbol{\phi},\boldsymbol{\theta}) = V(\boldsymbol{\phi},\boldsymbol{\theta})이면 zero-sum 공식을 복구한다. 제로섬 구조에서 벗어났지만 최적화의 내포된 형식은 일반적인 공식에서 남아 있다.
판별기와 생성기에 대한 개별적인 손실 함수 LDL_D와 LGL_G는 일반 형식을 따르므로 암시적 생성 모델을 효율적으로 학습하는데 사용할 수 있다. 따라서 대부분의 손실함수는 다음과 같이 작성할 수 있다.
LD(ϕ,θ)=Ep∗(x)g(Dϕ(x))+Eqθ(x)h(Dϕ(x))=Ep∗(x)g(Dϕ(x))+Eq(z)h(Dϕ(Gθ(z)))LG(ϕ,θ)=Eqθ(x)l(Dϕ(x))=Eq(z)l(Dϕ(Gθ(z)))\begin{aligned} L_D(\boldsymbol{\phi},\boldsymbol{\theta}) &= \mathbb{E}_{p^*(\bold{x})}g(D_{\boldsymbol{\phi}}(\bold{x})) + \mathbb{E}_{q_\theta(\bold{x})}h(D_{\boldsymbol{\phi}}(\bold{x})) \\& = \mathbb{E}_{p^*(\bold{x})}g(D_{\boldsymbol{\phi}}(\bold{x})) + \mathbb{E}_{q(\bold{z})}h(D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}))) \\ L_G(\boldsymbol{\phi},\boldsymbol{\theta}) &= \mathbb{E}_{q_\theta(\bold{x})}l(D_{\boldsymbol{\phi}}(\bold{x})) \\&= \mathbb{E}_{q(\bold{z})}l(D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}))) \end{aligned}
여기서 g,h,l:R→Rg,h,l : \mathbb{R} \to \mathbb{R}에 대해
g(t)=−log⁡t,h(t)=−log⁡(1−t),l(t)=log⁡(1−t)g(t) = -\log t, h(t) = -\log(1-t), l(t) = \log(1-t)이면 원래의 GAN을 복구하고,
LD(ϕ,θ)=−(Ep∗(x)log⁡Dϕ(x)+Eq(z)log⁡(1−(Dϕ(Gθ(z)))))LG(ϕ,θ)=Eq(z)(1−log⁡Dϕ(Gθ(z)))\begin{aligned} L_D(\boldsymbol{\phi},\boldsymbol{\theta}) &= -(\mathbb{E}_{p^*(\bold{x})}\log D_{\boldsymbol{\phi}}(\bold{x}) + \mathbb{E}_{q(\bold{z})}\log(1 - (D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}))))) \\ L_G(\boldsymbol{\phi},\boldsymbol{\theta}) &= \mathbb{E}_{q(\bold{z})}(1-\log D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}))) \end{aligned}
g(t)=−log⁡t,h(t)=−log⁡(1−t),l(t)=−log⁡(t)g(t) = -\log t, h(t) = -\log(1-t), l(t) = -\log(t)이면 non-saturating 손실이 되고,
LD(ϕ,θ)=−(Ep∗(x)log⁡Dϕ(x)+Eq(z)log⁡(1−(Dϕ(Gθ(z)))))LG(ϕ,θ)=−Eq(z)log⁡Dϕ(Gθ(z))\begin{aligned} L_D(\boldsymbol{\phi},\boldsymbol{\theta}) &= -(\mathbb{E}_{p^*(\bold{x})}\log D_{\boldsymbol{\phi}}(\bold{x}) + \mathbb{E}_{q(\bold{z})}\log(1 - (D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}))))) \\ L_G(\boldsymbol{\phi},\boldsymbol{\theta}) &= -\mathbb{E}_{q(\bold{z})}\log D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z})) \end{aligned}
g(t)=t,h(t)=−t,l(t)=tg(t) = t, h(t) = -t, l(t)=t이면 Wasserstein 거리 공식이 되고,
LD(ϕ,θ)=Ep∗(x)Dϕ(x)−Eq(z)Dϕ(Gθ(z))LG(ϕ,θ)=Eq(z)Dϕ(Gθ(z))\begin{aligned} L_D(\boldsymbol{\phi},\boldsymbol{\theta}) &= \mathbb{E}_{p^*(\bold{x})} D_{\boldsymbol{\phi}}(\bold{x}) - \mathbb{E}_{q(\bold{z})}D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z})) \\ L_G(\boldsymbol{\phi},\boldsymbol{\theta}) &= \mathbb{E}_{q(\bold{z})} D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}))\end{aligned}
g(t)=t,h(t)=−f†(t),l(t)=f†(t)g(t) = t, h(t) = -f^\dag(t), l(t) =f^\dag(t)이면 ff-divergence가 된다. 여기서 f†f^\dagger는 divergence 함수를 의미 함.
LD(ϕ,θ)=Ep∗(x)Dϕ(x)−Eq(z)Dϕ(Gθ(z))†LG(ϕ,θ)=Eq(z)Dϕ(Gθ(z))†\begin{aligned} L_D(\boldsymbol{\phi},\boldsymbol{\theta}) &= \mathbb{E}_{p^*(\bold{x})} D_{\boldsymbol{\phi}}(\bold{x}) - \mathbb{E}_{q(\bold{z})}D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}))^\dagger \\ L_G(\boldsymbol{\phi},\boldsymbol{\theta}) &= \mathbb{E}_{q(\bold{z})}D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}))^\dagger \end{aligned}

Training

판별기 손실 함수 LD(ϕ,θ)L_D(\boldsymbol{\phi},\boldsymbol{\theta})와 생성기 손실 LG(ϕ,θ)L_G(\boldsymbol{\phi},\boldsymbol{\theta})를 사용하는 일반적인 공식을 가정하자. 판별기가 거리나 발산 D(p∗,qθ)D(p^*,q_\theta)를 근사하도록 유도 되므로, 생성기가 해당 발산의 좋은 근사를 최소화하려면 각 생성기 업데이트마다 판별기 최적화를 완전히 해결해야 한다. 이것은 계산적으로 엄두도 내기 어렵기 때문에, 몇 개의 gradient 단계를 수행하여 판별기 파라미터를 업데이트 한 다음 생성기 업데이트를 수행하는 altering 업데이트의 동기가 된다.
Algorithm: altering update를 사용하는 General GAN 학습 알고리즘
1.
ϕ,θ\boldsymbol{\phi}, \boldsymbol{\theta} 초기화
2.
for 각 학습 반복 do
a.
for KK 단계 do
i.
gradient ∇ϕLD(ϕ,θ)\nabla_{\boldsymbol{\phi}} L_D(\boldsymbol{\phi},\boldsymbol{\theta})를 사용하여 판별기 파라미터 ϕ\boldsymbol{\phi} 업데이트
b.
gradient ∇θLG(ϕ,θ)\nabla_{\boldsymbol{\theta}} L_G(\boldsymbol{\phi},\boldsymbol{\theta})를 사용하여 생성기 파라미터 θ\boldsymbol{\theta} 업데이트
3.
ϕ,θ\boldsymbol{\phi}, \boldsymbol{\theta} 반환
따라서 ∇ϕLD(ϕ,θ)\nabla_{\boldsymbol{\phi}} L_D(\boldsymbol{\phi},\boldsymbol{\theta})와 ∇θLG(ϕ,θ)\nabla_{\boldsymbol{\theta}} L_G(\boldsymbol{\phi},\boldsymbol{\theta})를 계산하는데 관심이 있다. 판별기와 생성기 모두 방정식 일반적인 형식을 따르도록 손실 함수을 선택하면 학습에 사용할 수 있는 gradient를 계산할 수 있다.
우선 판별기 gradient를 계산하기 위해 다음과 같이 작성한다.
∇ϕLD(ϕ,θ)=∇ϕ[Ep∗(x)g(Dϕ(x))+Eqθ(x)h(Dϕ(x))]=Ep∗(x)∇ϕg(Dϕ(x))+Eqθ(x)∇ϕh(Dϕ(x))\begin{aligned} \nabla_{\boldsymbol{\phi}} L_D(\boldsymbol{\phi},\boldsymbol{\theta}) &= \nabla_{\boldsymbol{\phi}}[\mathbb{E}_{p^*(\bold{x})}g(D_{\boldsymbol{\phi}}(\bold{x})) + \mathbb{E}_{q_\theta(\bold{x})} h(D_{\boldsymbol{\phi}}(\bold{x}))] \\ &= \mathbb{E}_{p^*(\bold{x})} \nabla_{\boldsymbol{\phi}} g(D_{\boldsymbol{\phi}}(\bold{x})) + \mathbb{E}_{q_\theta(\bold{x})} \nabla_{\boldsymbol{\phi}} h(D_{\boldsymbol{\phi}}(\bold{x})) \end{aligned}
여기서 ∇ϕg(Dϕ(x))\nabla_{\boldsymbol{\phi}} g(D_{\boldsymbol{\phi}}(\bold{x}))와 ∇ϕh(Dϕ(x))\nabla_{\boldsymbol{\phi}} h(D_{\boldsymbol{\phi}}(\bold{x}))는 역전파를 통해 계산될 수 있고 각 기대는 몬테 카를로 추정을 사용하여 추정될 수 있다.
다음으로 생성기에 대해 다음의 gradient를 계산한다.
LG(ϕ,θ)=∇θEqθ(x)l(Dϕ(x))L_G(\boldsymbol{\phi},\boldsymbol{\theta}) = \nabla_{\boldsymbol{\theta}}\mathbb{E}_{q_\theta(\bold{x})} l(D_{\boldsymbol{\phi}}(\bold{x}))
여기서 적분 아래의 분포가 미분 파라미터 θ\boldsymbol{\theta}에 의존하므로 미분과 적분의 순서를 변경할 수 없다. 대신 qθ(x)q_\theta(\bold{x})가 암시적 생성 모델(또한 ‘reparameterization trick’으로 알려진)에 의해 유도된 분포임을 사용한다.
∇θLG(ϕ,θ)=∇θEqθ(x)l(Dϕ(x))=∇θEq(z)l(Dϕ(Gθ(z)))=Eq(z)∇θl(Dϕ(Gθ(z)))\begin{aligned} \nabla_{\boldsymbol{\theta}}L_G(\boldsymbol{\phi},\boldsymbol{\theta}) &= \nabla_{\boldsymbol{\theta}}\mathbb{E}_{q_\theta(\bold{x})}l(D_{\boldsymbol{\phi}}(\bold{x})) \\&= \nabla_{\boldsymbol{\theta}} \mathbb{E}_{q(\bold{z})} l(D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}))) \\&= \mathbb{E}_{q(\bold{z})} \nabla_{\boldsymbol{\theta}} l(D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}))) \end{aligned}
그리고 다시 몬테 카를로 추정을 사용하여 prior q(z)q(\bold{z}) 샘플을 사용하여 gradient를 근사한다. 위의 알고리즘에서 손실 함수의 선택과 몬테 카를로 추정을 교체하면 다음 알고리즘로 이어진다. 이것은 GAN을 학습할 때 자주 사용된다.
Algorithm: GAN 학습 알고리즘
1.
ϕ,θ\boldsymbol{\phi}, \boldsymbol{\theta} 초기화
2.
for 각 학습 반복 do
a.
for KK 단계 do
i.
MM개 노이즈 벡터 zm∼q(z)\bold{z}_m \sim q(\bold{z})의 미니배치 샘플
ii.
MM개 예제 xm∼p∗(x)\bold{ x}_m \sim p^*(\bold{x})의 미니배치 샘플
iii.
이 gradient를 사용하여 SGD를 수행하여 판별기 업데이트 ∇ϕ1M∑m=1M[g(Dϕ(xm))+∇ϕh(Dϕ(Gθ(zm)))]\nabla_{\boldsymbol{\phi}} {1\over M} \sum_{m=1}^M [g(D_{\boldsymbol{\phi}}(\bold{x}_m) ) + \nabla_{\boldsymbol{\phi}}h(D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}_m)))]
b.
MM개 노이즈 벡터 zm∼q(z)\bold{z}_m \sim q(\bold{z})의 미니배치 샘플
c.
이 gradient를 사용하여 SGD를 수행하여 생성기 업데이트 ∇θ1M∑m=1Ml(Dϕ(Gθ(zm))\nabla_{\boldsymbol{\theta}} {1\over M} \sum_{m=1}^M l(D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}_m))
3.
ϕ,θ\boldsymbol{\phi}, \boldsymbol{\theta} 반환

Mode Collapse, Mode Hopping

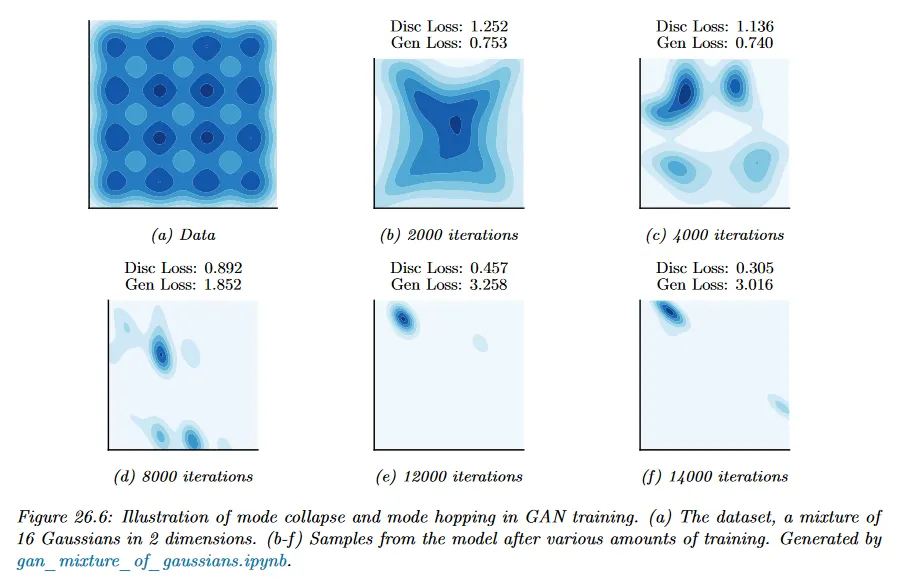
GAN의 적대적 게임 특성 때문에 GAN의 최적화 다이나믹스는 이론적으로도 어렵고 실제로 안정화 하기도 어렵다. GAN은 생성기가 데이터 분포의 모든 모드를 커버하지 않는 분포로 수렴하여 모델이 분포에 underfit하는 현상인 mode collapse에 시달린다. 아래 그림 26.5 참조.
데이터는 16개 모드의 가우시안 혼합이지만 모델은 몇 개의 모드만 커버한다. 또 다른 문제가 있는 동작은 mode hopping이다. 여기서 생성기는 데이터 분포의 서로 다른 모드를 생성하는 사이를 ‘hop(깡총 뛰다)’한다. 이 행동에 대한 직관적인 설명은 다음과 같다. 생성기가 하나의 모드에서 데이터를 생성하는 것에서 익숙해지면 해당 모드에서 더 많은 데이터를 생성한다. 판별기가 이 모드에서 실제와 생성된 데이터 사이의 구별을 제대로 학습하지 못하면 생성기는 이 지지를 확장하고 다른 모드에서 데이터를 생성할 인센티브가 없다. 반면에 판별기가 결국 실제와 이 모드 내에서 실제 데이터와 생성된 데이터 구별하는 방법을 학습하면 생성기는 간단히 새로운 모드로 움직이고(hop), 이 고양이와 쥐 게임은 계속된다.
모드 붕괴와 모드 호핑은 GAN과 연관되어 있지만 많은 개선으로 GAN 학습은 더 안정적이게 되었고 이런 동작이 더욱 드물어졌다. 이러한 개선에는 large batch size, 판별기 신경망 수용량을 증가시키는 것, 판별기와 생성기 규제를 사용하는 것, 더 복잡한 최적화 방법을 사용하는 것 등이 포함된다.

Conditional GANs

GAN에 대해 p∗(x∣y)p^*(\bold{x}|\bold{y}) 형식의 조건부 분포를 학습할 수 있으면 유용하다. 암시적 조건부 모델 qθ(x∣y)q_\theta(\bold{x}|\bold{y})를 학습하기 위해 데이터와 연관된 조건부 정보를 지정하는 데이터셋이 필요하고 모델 아키텍쳐와 손실 함수를 채택해야 한다. GAN의 경우에 critic이 생성기의 손실 함수의 일부이기 때문에 critic을 변경하여 생성 모델의 손실 함수를 변경 할 수 있다. 현실적인 샘플을 제공하지만 제공된 조건을 무시하는 생성기에 페널티를 부여하여 조건 정보를 설명하는 학습 신호를 제공하는 것이 critic에 중요하다.
min-max 게임의 형식을 변경하지 않고 두 플레이어에게 조건부 정보를 제공하면 원래 GAN 게임에서 conditional GAN을 생성할 수 있다.
min⁡θmax⁡ϕ12Ep(y)Ep∗(x∣y)[log⁡Dϕ(x,y)]+12Ep(y)Eqθ(x∣y)[log⁡(1−Dϕ(x,y))]\min_{\boldsymbol{\theta}} \max_{\boldsymbol{\phi}}{1\over2} \mathbb{E}_{p(\bold{y})} \mathbb{E}_{p^*(\bold{x}|\bold{y})} [\log D_{\boldsymbol{\phi}}(\bold{x},\bold{y})] + {1\over2}\mathbb{E}_{p(\bold{y})} \mathbb{E}_{q_\theta(\bold{x}|\bold{y})}[\log (1-D_{\boldsymbol{\phi}}(\bold{x},\bold{y}))]
암시적 잠재 변수 모델의 경우에 임베딩 정보는 잠재 변수 z\bold{z}와 함께 생성기에 대한 추가 입력이 된다.
min⁡θmax⁡ϕL(θ,ϕ)=12Ep(y)Ep∗(x∣y)[log⁡Dϕ(x,y)]+12Ep(y)Eq(z)[log⁡(1−Dϕ(Gθ(z,y),y))]\begin{aligned} \min_{\boldsymbol{\theta}} \max_{\boldsymbol{\phi}}\mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi}) &= {1\over2} \mathbb{E}_{p(\bold{y})} \mathbb{E}_{p^*(\bold{x}|\bold{y})} [\log D_{\boldsymbol{\phi}}(\bold{x},\bold{y})] \\ &+ {1\over2}\mathbb{E}_{p(\bold{y})} \mathbb{E}_{q(\bold{z})}[\log (1-D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z},\bold{y}),\bold{y}))] \end{aligned}
라벨 같은 이산 조건 정보에 대해 실제와 가짜 데이터를 구별하는 방법을 학습할 뿐만 아니라 데이터셋에서 주어진 KK개 클래스 중 하나와 관련된 데이터와 생성된 샘플을 모두 분류하는 방법을 학습하는 critic을 학습하여 새로운 손실 함수를 추가할 수 있다.
Lc(θ,ϕ)=−[12Ep(y)Ep∗(x∣y)[log⁡Dϕ(y∣x)]+12Ep(y)Eqθ(x∣y)[log⁡Dϕ(y∣z))]]\mathcal{L}_c(\boldsymbol{\theta},\boldsymbol{\phi}) = -\left[ {1\over2} \mathbb{E}_{p(\bold{y})} \mathbb{E}_{p^*(\bold{x}|\bold{y})} [\log D_{\boldsymbol{\phi}}(\bold{y}|\bold{x})] + {1\over2}\mathbb{E}_{p(\bold{y})} \mathbb{E}_{q_\theta(\bold{x}|\bold{y})}[\log D_{\boldsymbol{\phi}}(\bold{y}|\bold{z}))] \right]

Sample Code

Model

생성기와 판별기는 아래처럼 구성한다.
생성기는 처음에 무작위 노이즈 벡터를 입력으로 받아 선형 변환(linear) 한 후에 conv 레이어를 통과하면서 입력을 점차적으로 이미지로 변환한다.
# 생성기 모델 정의 class Generator(nn.Module): def __init__(self, img_size=64, channels=3, latent_dim=100): super(Generator, self).__init__() self.init_size = img_size // 4 self.l1 = nn.Sequential(nn.Linear(latent_dim, 128 * self.init_size ** 2)) self.conv_blocks = nn.Sequential( nn.BatchNorm2d(128), nn.Upsample(scale_factor=2), nn.Conv2d(128, 128, 3, stride=1, padding=1), nn.BatchNorm2d(128, 0.8), nn.LeakyReLU(0.2, inplace=True), nn.Upsample(scale_factor=2), nn.Conv2d(128, 64, 3, stride=1, padding=1), nn.BatchNorm2d(64, 0.8), nn.LeakyReLU(0.2, inplace=True), nn.Conv2d(64, channels, 3, stride=1, padding=1), nn.Tanh() ) def forward(self, z): out = self.l1(z) out = out.view(out.shape[0], 128, self.init_size, self.init_size) img = self.conv_blocks(out) return img
Python
복사
판별기는 conv을 이용해서 계층을 구성하고 마지막에 이미지가 real인지 fake인지를 구별하는 하나의 값을 출력한다.
# 판별기 모델 정의 class Discriminator(nn.Module): def __init__(self, channels=3): super(Discriminator, self).__init__() self.model = nn.Sequential( nn.Conv2d(channels, 64, 3, 2, 1), nn.LeakyReLU(0.2, inplace=True), nn.Conv2d(64, 128, 3, 2, 1), nn.BatchNorm2d(128), nn.LeakyReLU(0.2, inplace=True), nn.Conv2d(128, 256, 3, 2, 1), nn.BatchNorm2d(256), nn.LeakyReLU(0.2, inplace=True), nn.Conv2d(256, 512, 3, 2, 1), nn.BatchNorm2d(512), nn.LeakyReLU(0.2, inplace=True), nn.Flatten(), nn.Linear(512 * 4 * 4, 1), ) def forward(self, img): validity = self.model(img) return validity
Python
복사

Objective, Train

Wasserstein GAN의 loss 함수를 따라 판별기와 생성기의 손실을 구성한다.
판별기는 real과 생성기가 만든 fake를 모두 판별한 다음 두 결과의 평균의 차이를 구하는 형태로 loss를 구성한다. 판별기가 real에 대해 더 높은 점수를 부여하고, fake에 대해 낮은 점수를 부여하고 real에 대해서는 높은 점수가 나오므로 최종 loss가 낮게 나오도록 fake에 높은 점수를 부여하도록 학습된다.
LD(ϕ,θ)=Ep∗(x)Dϕ(x)−Eq(z)Dϕ(Gθ(z))L_D(\boldsymbol{\phi},\boldsymbol{\theta}) = \mathbb{E}_{p^*(\bold{x})} D_{\boldsymbol{\phi}}(\bold{x}) - \mathbb{E}_{q(\bold{z})}D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}))
생성기는 판별기와 달리 매번 업데이트 하지 않고 n_critic 당 1회씩만 업데이트 한다. 생성기가 생성한 이미지를 판별기에 넣은 값에 평균을 취하도록 loss를 구성한다. 이렇게 함으로써 생성기가 fake에 대한 판별기의 판정이 작게 나오도록 학습되게 한다.
LG(ϕ,θ)=Eq(z)Dϕ(Gθ(z))L_G(\boldsymbol{\phi},\boldsymbol{\theta}) = \mathbb{E}_{q(\bold{z})} D_{\boldsymbol{\phi}}(G_{\boldsymbol{\theta}}(\bold{z}))
추가로 안정적인 학습을 위해 판별기의 파라미터에 대해 가중치가 Lipschitz 조건을 만족하도록 clamp 한다.
# 하이퍼파라미터 설정 latent_dim = 100 batch_size = 64 epochs = 100 lr = 0.00005 n_critic = 5 clip_value = 0.01 img_size = 64 channels = 3 sample_interval = 400 # 데이터 전처리 transform = transforms.Compose([ transforms.Resize(img_size), transforms.CenterCrop(img_size), transforms.ToTensor(), transforms.Normalize([0.5]*channels, [0.5]*channels) ]) # LFW 데이터셋 로드 data_path = "./data/lfw" os.makedirs(data_path, exist_ok=True) dataloader = DataLoader( datasets.LFWPeople(root=data_path, download=True, transform=transform), batch_size=batch_size, shuffle=True ) # 모델 초기화 generator = Generator() discriminator = Discriminator() # CUDA 사용 가능 여부 확인 device = torch.device("cuda" if torch.cuda.is_available() else "cpu") generator = generator.to(device) discriminator = discriminator.to(device) # 손실 함수 및 옵티마이저 설정 optimizer_G = torch.optim.RMSprop(generator.parameters(), lr=lr) optimizer_D = torch.optim.RMSprop(discriminator.parameters(), lr=lr) # 훈련 루프 for epoch in range(epochs): for i, (imgs, _) in enumerate(dataloader): # 이미지 데이터 준비 real_imgs = imgs.to(device) # 판별기 훈련 optimizer_D.zero_grad() z = torch.randn(imgs.shape[0], latent_dim).to(device) # 생성기가 만든 fake 이미지 fake_imgs = generator(z).detach() # 판별기 loss d_loss = torch.mean(discriminator(real_imgs)) - torch.mean(discriminator(fake_imgs)) d_loss.backward() optimizer_D.step() # 판별기 매개변수 클리핑 # 판별기의 가중치가 너무 커지거나 작아지는 것을 방지해서 Lipschitz 조건을 만족하게 한다. for p in discriminator.parameters(): p.data.clamp_(-clip_value, clip_value) # n_critic 배수로 생성기 훈련 if i % n_critic == 0: optimizer_G.zero_grad() # 매번 업데이트 하지 않기 때문에 여기서 새로 생성한다. gen_imgs = generator(z) # 생성기 loss g_loss = torch.mean(discriminator(gen_imgs)) g_loss.backward() optimizer_G.step() # 로그 및 이미지 저장 if i % sample_interval == 0: print(f"[Epoch {epoch}/{epochs}] [Batch {i}/{len(dataloader)}] [D loss: {d_loss.item()}] [G loss: {g_loss.item()}]") save_image(gen_imgs.data[:25], f"images/{epoch:03d}_{i:03d}.png", nrow=5, normalize=True) print("Training completed!")
Python
복사
아래는 위 코드의 실행 결과. 최초에는 noise에 가까운 이미지였다가 점차 사람처럼 보이는 이미지가 생성되고, 100번째 epoch에서 좀 더 사람처럼 보이는 이미지가 만들어진다.
•
epoch 1
•
epoch 50
•
epoch 100

참고

Made with