1 Introduction
이전 노트에서 장면에 대해 추가 viewpoint를 더하면 해당 장면에 대한 지식을 크게 향상시킬 수 있음을 다루었다. 3d 장면에 관한 정보를 추출하지 않고도 한 이미지 평면의 점을 다른 이미지 평면의 점에 관련지을 수 있도록 epipolar geometry 설정에 초점을 맞추었다. 이번 강의에서는 여러 2d 이미지에서 3d 장면에 관한 정보를 복구하는 방법에 대해 논의한다.
2 Triangulation
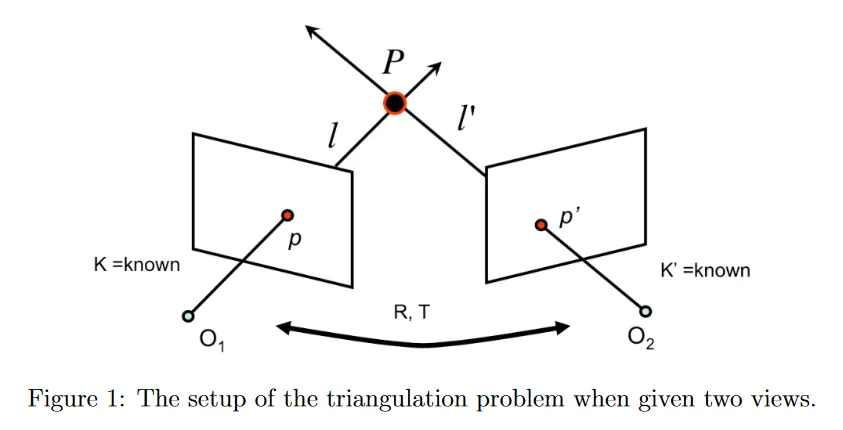
여러 view geometry에서 가장 근본적인 문제 중 하나는 triangulation(삼각측량) 문제이다. 이는 3d 점의 위치를 2개 이상의 이미지에 투영된 것으로부터 결정하는 과정이다.
두 view에서의 triangulation 문제에서는 각각 알려진 카메라 intrinsic 파라미터 와 를 가진 2대의 카메라를 갖는다. 또한 이 카메라들의 상대적인 orientation과 offset 를 갖는다. 3d에 점 가 있다고 가정하자. 이것은 두 카메라의 이미지에서 각각 와 에 해당한다. 의 위치가 현재 알려지지 않지만 이미지에서 와 의 정확한 위치를 측정할 수 있다. 가 알려져 있으므로 카메라 중심 와 이미지 위치 에 의해 정의되는 두 시선 과 을 계산할 수 있다. 따라서 는 과 의 교점으로 계산될 수 있다.
이 절차가 간단하고 수학적으로 타당해 보이지만, 실제로는 잘 작동하지 않는다. 왜냐하면 현실에서 관측치 와 가 noisy이고 camera calibration 파라미터가 정밀하지 않기 때문에 과 의 교차점을 찾는 것이 문제가 있다. 대부분의 경우에서 두 선이 교차하지 않으므로 교점이 전혀 존재하지 않을 수 있다.
2.1 A linear method for triangulation
이 섹션에서 ray 사이의 교차 점의 부재를 해결하는 간단한 linear triangulation 방법을 설명한다. 서로 대응하는 두 이미지의 점이 와 로 주어진다. cross product의 정의에 따라 이다. cross product에 의해 생성된 등식을 명시적으로 사용하여 3가지 제약조건을 형성할 수 있다.
여기서 는 행렬 의 -번째 행이다. 유사한 제약조건을 와 에 대해 형식화할 수 있다. 두 이미지의 제약조건을 사용하여 형식의 선형 방정식을 형식화할 수 있다. 여기서
이 등식은 점 의 best linear 추정치를 찾기 위해 SVD를 사용하여 해결될 수 있다. 이 방법의 또 다른 흥미로운 측면은 여러 view에서 triangulating도 잘 다룰 수 있다는 것이다. 그렇게 하기 위해 새로운 view에 의해 추가된 제약조건에 해당하는 행을 에 추가하면 된다.
그러나 이 방법은 projective-invariant이 아니기 때문에 projective reconstruction에 적합하지 않다. 예컨대 카메라 행렬 을 projective transformation 에 의해 영향 받는 것으로 교체한다고 가정하자. 그러면 선형 방정식의 행렬 는 이 된다. 그러므로 이전 추정치 의 해 는 변환된 문제 의 해 에 해당한다. SVD는 의 제약조건을 해결하지만 이것은 projective transformation 에 대해 불변이 아니다. 그러므로 이 방법은 간단하지만 종종 triangulation 문제의 최적 해가 아니다.
2.2 A nonlinear method for triangulation
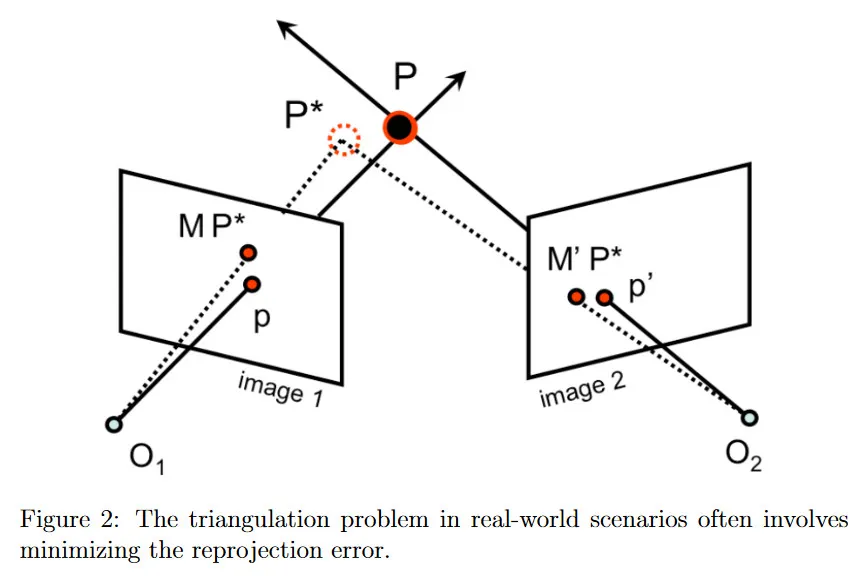
대신 현실 세계 시나리오에 대한 triangulation 문제는 종종 수학적으로 최소화 문제를 해결하는 것으로 특성화 된다.
위의 방정식에서 우리는 두 이미지에서 의 reprojection error의 best least-square을 찾음으로써 를 가장 잘 근사하는 3d 공간의 를 찾는다. 이미지에서 3d 점에 대한 reprojection error는 그 점을 이미지에 projection 한 것과 이미지 평면에서 관측된 대응점 사이의 거리이다. 그림 2의 예시에서 은 3d 공간에서 이미지 1에 대한 projective transformation이므로 를 이미지 1에 project한 점은 이다. 이미지 1에서 에 대응하는 관측치는 이다. 따라서 이미지 1에 대한 reprojection error는 거리 이다. 방정식 2.3에서 발견한 전체 reprojection error는 모든 이미지에 걸친 reprojection error의 합이다. 2개 이상의 이미지가 있는 경우에 목적 함수에 거리 항을 더 추가하기만 하면 된다.
실제에서 문제에 대한 좋은 근사치를 얻을 수 있는 다양한 정교한 최적화 방법이 존재한다. 그러나 이 수업의 범위에서 우리는 이러한 기법들 중 하나인 nonlinear least squares에 대한 Gauss-Newton algorithm에만 초점을 맞춘다. 일반적인 nonlinear least squares 문제는 다음을 최소화하는 을 찾는 것이다.
여기서 은 어떤 함수 , 입력 와 관찰 에 대해 와 같은 임의의 residual function 이다. 함수 가 선형일 때 nonlinear least squares 문제는 regular linear least square 문제로 축소된다. 그러나 일반적으로 우리의 카메라 행렬이 affine이 아님을 떠올려라. 왜냐하면 이미지 평면에 대한 projection이 종종 homogeneous 좌표로 나누기 때문이다. 이미지에 대한 projection은 일반적으로 비선형이다.
를 벡터 로 (원문에는 로 되어 있지만 오타인 듯) 설정하면 최적화 문제를 다음과 같이 재형식화 할 수 있다.
이것은 완벽하게 nonlinear least squares 문제로 표현될 수 있다.
이 노트에서 Gauss-Newton algorithm을 사용하여 이 nonlinear least squares 문제에 대한 근사 해를 찾는 방법을 다룬다. 우선 이전 선형 방법으로 계산될 수 있는 3d 점 에 대한 합리적인 추정치가 있다고 가정한다. Guass-Newton algorithm의 핵심 통찰은 reprojection error를 최소화하는 더 나은 추정치 방향으로 현재 추정치를 보정하여 업데이트하는 것이다. 각 단계에서 추정치 를 어떤 만큼 업데이트한다.
그러나 업데이트 파라미터 를 어떻게 선택할 수 있을까? Gauss-Newton 알고리즘의 핵심 통찰은 현재 추정치 근처에서 residual 함수를 선형화하는 것이다. 우리 문제의 경우 이것은 점 의 residual error 를 다음과 같이 생각할 수 있다는 것을 의미한다.
결과적으로 최소화 문제를 다음으로 변환한다.
이와 같이 residual을 형식화하면 표준 linear least squares 문제의 형식을 취하는 것을 볼 수 있다. 개 이미지에 대한 triangulation 문제에 대해 linear least squares 해는 다음이 된다.
여기서
그리고
특정한 이미지의 residual error 벡터 는 이미지 평면에서 두 차원이 존재하기 때문에 벡터이다. 따라서 triangulation의 가장 단순한 두 개의 카메라 경우 (), residual vector 는 벡터가 되고 야코비안 는 행렬이 된다. 추가 이미지는 벡터와 행렬에 해당하는 행을 추가하여 처리되므로 이 방법이 multiple view를 seamlessly 다룰 수 있음을 알 수 있다. 업데이트 를 계산한 후에 고정된 단계 수만큼 또는 수치적으로 수렴할 때까지 이 과정을 반복하면 된다. Gauss-Newton 알고리즘의 가장 중요한 속성 중 하나는 residual function가 우리의 추정치 근처에서 선형이라는 가정이 수렴을 보장하지 않는다는 것이다. 따라서 실제로는 추정치에 대한 업데이트 횟수에 상한을 두는 것이 항상 유용하다.
3 Affine structure from motion
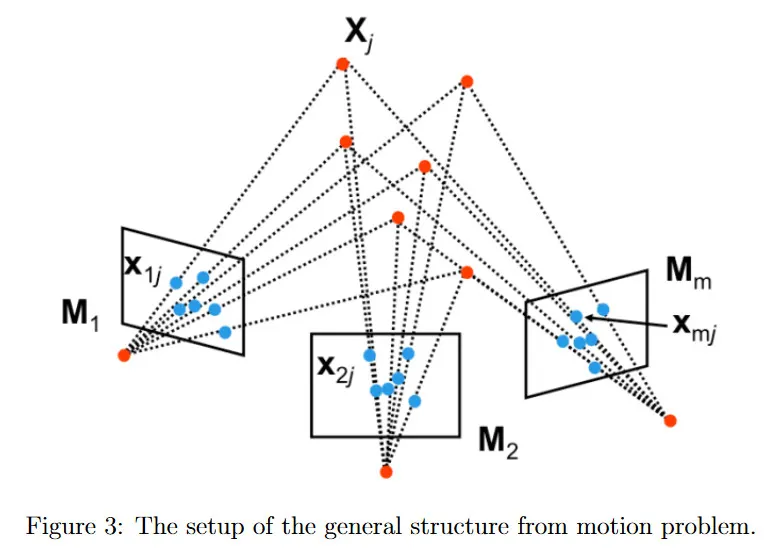
이전 섹션의 마지막 부분에서 장면의 두 view를 너머 3d 장면에 관한 정보를 얻을 수 있음을 시사했다. 이제 두 대의 카메라의 geometry를 multiple 카메라로 확장하는 방법을 탐구한다. multiple view에서 관찰 점을 결합하여 structure from motion으로 알려진대로 장면의 3d 구조와 카메라의 파라미터 모두를 동시에 결정할 수 있다.
여기서 structure from motion 문제를 형식적으로 유도한다. 개의 카메라에 대해 intrinsic과 extrinsic 파라미터 모두를 인코딩하는 카메라 변환 가 있다고 가정하자. 를 장면의 개 3d 포인트 중 하나라고 하자. 각 3d point는 multiple 카메라에서 볼 수 있으며, 는 를 projective transformation 를 사용하여 카메라 의 이미지로 projection한 것이다. structure from motion의 목표는 모든 관찰 에서 장면의 structure(개 3d 점 )와 카메라의 motion(개 projection 행렬 ) 모두를 복구하는 것이다.
3.1 The affine structure from motion problem
일반적인 structure from motion 문제를 다루기 전에 우선 카메라가 affine 또는 weak perspective라고 가정하는 더 간단한 문제부터 시작한다. 궁극적으로 perspective scaling 연산이 없어지면 이 문제에 대한 수학적 유도가 더 쉬워진다.
이전에 perspective와 weak perspective 경우에 대해 위의 등식을 유도했다. full perspective 모델에서 카메라 행렬이 다음과 같이 정의되는 것을 떠올려라.
여기서 는 어떤 non-zero 벡터이다. 반면에 weak perspective model의 경우 이다. 이 속성은 의 homogeneous 좌표를 1과 동일하게 만든다.
결과적으로 homogeneous에서 유클리드 좌표로 이동하면서 projective transformation의 비선형성은 사라지고 weak perspective transformation은 더 magnifier(확대기) 역할을 한다. 우리는 projection을 다음과 같이 더 간결하게 나타낼 수 있다.
그리고 모든 카메라 행렬을 형식으로 나타낼 수 있다. 따라서 우리는 이제 affine 카메라 모델을 사용하여 3d에서 점 과 각 affine 카메라에서의 대응 관측치간의 관계(예컨대 카메라 에서 )를 표현할 수 있다.
structure from motion 문제로 돌아가서, 우리는 개 관찰에서 개 행렬 와 개 월드 좌표 벡터 , 총 개의 미지수를 추정해야 한다. 각 관측치는 카메라당 2개의 제약을 생성하므로 개의 미지수에 대해 방정식이 존재한다. 우리는 이 방정식을 사용하여 각 이미지에서 대응점이 필요한 최소 개수의 하한을 알 수 있다. 예컨대 개의 카메라를 가지면, 3d에서 최소 개의 점이 필요하다. 그러나 각 이미지에서 라벨링된 대응점을 충분하면, 이 문제를 어떻게 해결할 수 있는가?
3.2 The Tomasi and Kanade factorization method
이 파트에서 우리는 affine structure from motion 문제를 해결하기 위한 Tomasi와 Kanade의 fatorization 방법을 개략적으로 설명한다. 이 방법은 2가지 주요 단계로 구성된다. data centering step과 actual factorization step.
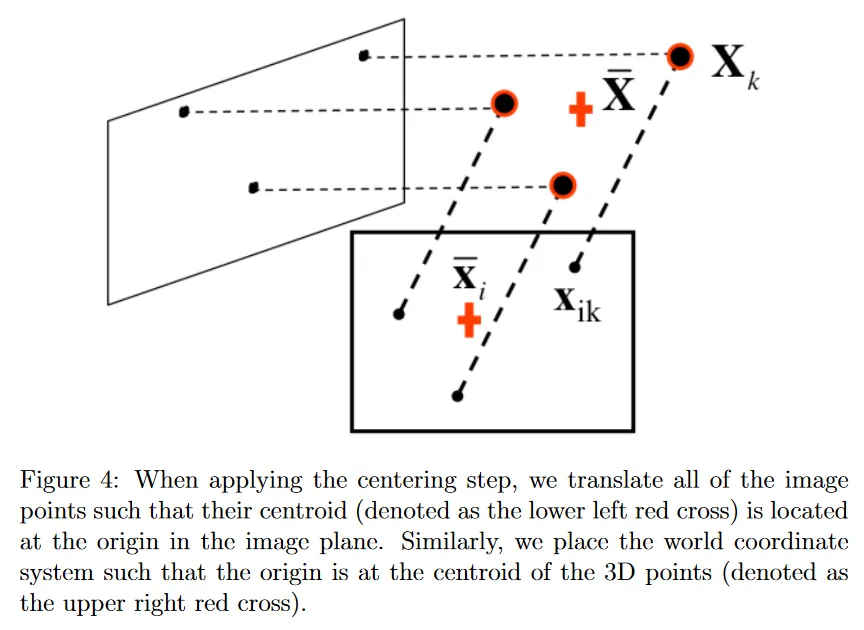
data centering 단계에서 시작하자. 이 단계에서 주요 아이디어는 원점에 데이터를 center하는 것이다. 이것을 위해 각 이미지 에 대해 각 이미지 점 에 대해 그들의 centroid 를 빼서 새로운 좌표 를 재정의한다.
affine structure from motion 문제가 이미지 포인트 , 카메라 행렬 변수 와 그리고 3d 점 사이의 관계가 다음과 같음을 떠올려라.
이 centering 단계 이후에, 방정식 3.4의 centered 이미지 점 의 정의와 방정식 3.5에서 affine 표현식을 결합할 수 있다.
방정식 3.6에서 볼 수 있듯이, world reference system의 원점을 centroid 로 translate 하면 이미지 점의 centered 좌표 와 3d 점의 centered 좌표 는 단일 행렬 에 의해서만 연관된다. 궁극적으로 factorization 방법의 centering 단계를 통해 3d 구조와 multiple 이미지에서의 관측 점 간의 관계를 간편한 행렬 곱 표현으로 만들 수 있다.
그러나 행렬 곱 에서 등식의 좌변의 값에만 접근할 수 있음에 유의하라. 따라서 어떻게든 motion 행렬 와 구조 를 인수분해 해야 한다. 개 카메라에 대한 모든 관찰을 사용하여 개의 관찰으로 이루어진 measurement matrix 를 구축할 수 있다. (각 항목이 벡터임을 기억하라)
이제 affine 가정 때문에 가 motion matrix (이것은 카메라 행렬 로 구성됨)과 structure matrix (이것은 3d 점 으로 구성됨)의 곱으로 표현될 수 있음을 떠올려라. 중요한 사실은 가 최대 차원이 인 두 행렬의 곱이므로 을 사용할 수 있다는 것이다.
를 과 로 인수분해하여, SVD 를 사용할 수 있다. 이므로 에는 3개의 non-zero singular value 만 존재한다. 따라서 표현식을 더 축소하여 다음의 분해를 얻을 수 있다.
이 decomposition에서 은 non-zero singular 값으로 이루어진 대각 행렬이며, 과 은 각각 와 의 3개 열과 행을 각각 취하여 얻어진다. 불행히도 실제에서 측정 noise와 affine 카메라 근사치 때문에 이다. 그러나 일 때 이 여전히 Frobenius norm의 관점에서 의 가장 좋은 rank-3 근사이다.
자세히 보면, 행렬 곱 이 행렬로 structure 행렬 와 정확히 동일한 크기이고, 유사하게 는 행렬로 motion 행렬 과 동일한 크기이다. SVD decomposition의 성분을 과 에 연관하는 방법은 affine structure from motion 문제에 대한 물리적, 기하학적으로 타당한 해를 제공하지만 이 선택이 유일한 해는 아니다. 예컨대 motion 행렬을 으로 structure 행렬을 로 설정해도 관찰 행렬 는 동일하다. 그렇다면 어떤 factorization을 선택해야 하는가? Tomasi와 Kanade는 그들의 논문에서 견고한 factorization의 선택은 과 라고 결론 내렸다.
3.3 Ambiguity in reconstruction
그럼에도 불구하고, 의 factorization 선택에 본질적인 모호성을 발견할 수 있다. 이는 임의의 가역인 행렬 를 decomposition에 추가할 수 있기 때문이다.
이것은 motion 에서 얻은 카메라 행렬과 structure 에서 얻은 3d 점이 공통 행렬 에 의해 곱해진 것으로 결정됨을 뜻한다. 그러므로 우리 해는 under-determined 이고 이 affine ambiguity를 해결하기 위해 추가 제약조건이 필요하다. reconstruction이 affine ambiguity를 가질 때, 평행성은 보존되지만 metric scale은 알 수 없음을 의미한다.
reconstruction을 위한 또 다른 중요한 ambiguities 클래스는 similarity ambiguity이다. 이것은 reconstruction이 similarity transform(rotation, translation, scaling)까지만 정확할 때 발생한다. similarity ambiguity만 갖는 reconstruction을 metric reconstruction이라 한다. 이 ambiguity는 카메라가 intrinsically calibrated이더라도 존재한다. 좋은 소식은 calibrated 카메라의 경우 similarity ambiguity는 유일한 ambiguity이라는 것이다.
이미지에서 장면의 절대 scale을 복구하는 방법이 없다는 사실은 꽤 직관적이다. 추가 가정(예: 그림에서 집의 높이를 알고 있음) 또는 더 많은 데이터를 통합하지 않는한, 객체의 scale, 절대 위치와 canonical orientation은 항상 알려지지 않는다. 이는 일부 특성이 다른 것에 대해 compensate(보상하다)할 수 있기 때문이다. 예컨대 동일한 이미지를 얻으려면 객체를 뒤로 이동시키고 그에 따라 scale만 하면 된다. similarity ambiguity을 제거하는 한 가지 예는 camera calibration 절차에서 발생했는데, 여기서 world reference system에 대한 calibration 점의 위치를 알고 있다고 가정했다. 이를 통해 3d 구조의 metric scale을 학습하기 위해 체커보드의 정사각형의 크기를 알 수 있었다.
4 Perspective structure from motion
motion 문제에서 단순화된 affine structure를 공부한 후에 projective 카메라 에 대한 일반적인 경우를 고려한다. projective 카메라의 일반적인 경우, 각 카메라 행렬 는 scale까지 정의되어 11개 자유도를 포함한다.
게다가 affine 경우에서 해가 affine transformation까지만 결정될 수 있었던 것처럼 일반적인 경우에 structure와 motion에 대한 해는 projective transformation까지만 결정될 수 있다. structure matrix에 inverse transformation 를 적용하는 한, motion matrix에 임의의 projective transformation 를 적용할 수 있다. 이미지 평면에서 결과 관측치는 여전히 동일할 것이다.
affine 경우와 유사하게 motion 문제에서 일반적인 structure를 개 관찰 에서 개 motion 행렬 과 개 3d 점 모두를 추정하여 설정할 수 있다. 카메라와 포인트는 projective transformation(15개 파라미터)까지 scale까지만 복구될 수 있기 때문에 개의 등식에서 개의 미지수를 갖는다. 이러한 사실에서 미지수를 해결하기 위해 필요한 view와 관찰의 수를 결정할 수 있다.
4.1 The algebraic approach
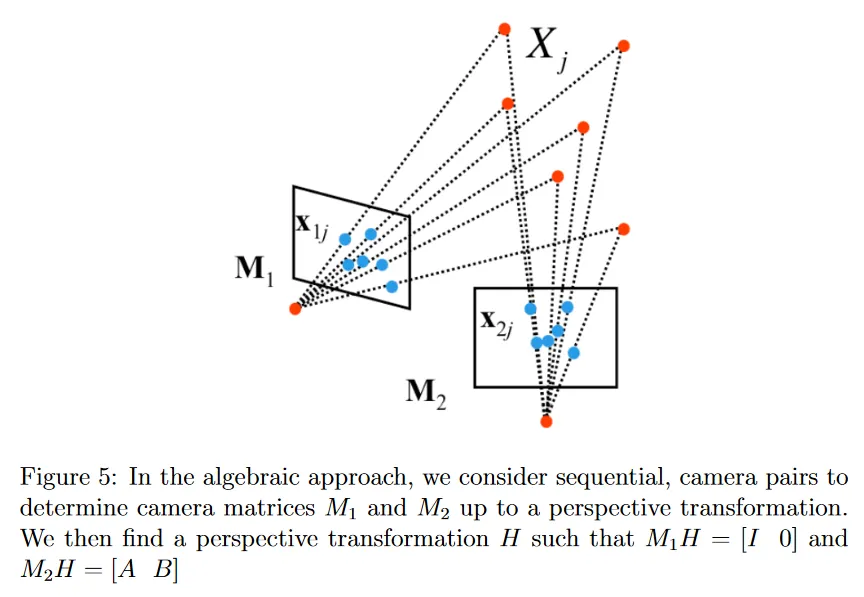
이제 algebraic(대수) 접근을 다룬다. 이것은 2대의 카메라에서 structure from motion 문제를 해결하기 위해 Fundamental 행렬 의 개념을 활용한다. 그림 5와 같이 대수 접근의 주요 아이디어는 perspective transformation 까지만 계산할 수 있는 2대 카메라 행렬 과 를 계산하는 것이다. 각 가 perspective transformation 까지만 계산할 수 있기 때문에 첫 번째 카메라 projection 행렬 이 canonical인 를 항상 고려할 수 있다. 물론 동일한 변환이 두 번째 카메라에도 적용될 수 있다.
이 작업을 수행하기 위해 먼저 이전 코스에서 다루었던 eight point algorithm을 사용하여 Fundamental 행렬 를 계산해야 한다. 이제 를 사용하여 projective 카메라 행렬 과 를 추정한다. 이 추정을 하기 위해 를 이미지의 대응 관측치 와 에 대한 대응 3d 점이라고 정의한다. 을 두 카메라 projection 행렬에 적용하기 때문에 도 structure에 적용해야 한다. 따라서 가 된다. 그러므로 픽셀 좌표 와 를 다음처럼 변환된 구조에 연관시킬 수 있다.
두 이미지 대응점 와 사이의 흥미로운 속성이 일부 창의적인 대체에 의해 나타난다.
방정식 4.4를 사용하여 와 사이에 cross product를 작성할 수 있다.
cross product의 정의에 따라 는 에 수직이다. 그러므로 다음과 같이 작성할 수 있다.
이 제약조건을 보면 Fundamental 행렬 의 일반적인 정의가 떠오를 것이다. 로 설정하면 와 를 추출하는 것은 decomposition 문제로 간단히 분해된다.
를 결정하는 것에서 시작하자. 다시 cross product의 정의에 의해 를 다음과 같이 간단히 작성할 수 있다.
가 singular이므로 는 SVD를 사용하여 인 의 least square 해로 계산될 수 있다.
을 알면 를 계산할 수 있다. 로 설정하면 이 정의가 를 만족하는 것을 확인할 수 있다.
결과적으로 카메라 행렬 과 에 대한 두가지 표현식을 결정할 수 있다.
이 섹션을 마무리하기 전에 에 대한 geometrical 해석을 제공한다. 우리는 가 을 만족한다는 것을 안다. 이전 코스 노트에서 유도한 epipolar 제약조건을 떠올려라. 이는 이미지에서 epipole이 Fundamental 행렬에 의해 변환될 때 0에 매핑되는 점이라는 것을 발견했다(즉 과 ). 그러므로 는 epipole임을 볼 수 있다. 이를 통해 카메라 projection 행렬에 대한 새로운 방정식 집합(방정식 4.10)을 얻는다.
4.2 Determining motion from the Essential matrix
대수적 접근으로 얻은 재구성을 개선하는 한 가지 유용한 방법은 calibrated 카메라를 사용하는 것이다. normalized 좌표에 대한 Fundamental 행렬의 특별한 경우인 Essential 행렬을 사용하여 카메라 행렬의 더 정확한 초기 추정을 추출할 수 있다. Essential 행렬 을 사용함으로써 카메라를 calibrate 하고 따라서 intrinsic 카메라 행렬 를 안다고 가정 한다. 우리는 normalized 이미지 좌표에서 직접 Essential 행렬 를 계산하거나 Fundamental 행렬 과 intrinsic 행렬 의 관계에서 계산할 수 있다.
Essential 행렬이 calibrate 된 카메라를 가졌다고 가정하기 때문에 extrinsic 파라미터를 인코딩하는 5개의 자유도(두 카메라 사이의 rotation 과 translation )만 갖는다는 것을 기억해야 한다. 다행히 이것은 우리의 motion 행렬을 생성하기 위해 추출하기를 원하는 정확한 정보이다. 우선 Essential 행렬 가 다음과 같이 표현될 수 있음을 떠올려라.
이와 같이, 아마도 를 두 성분으로 분해하는 전략을 발견할 수 있다. 우선 cross product 행렬 가 skew-symmetric이라는 것에 유의하라. 우리는 decomposition에서 사용할 2개의 행렬을 정의한다.
나중에 사용할 중요한 속성 하나는 부호까지 라는 것이다. 유사하게 부호까지 라는 사실을 사용할 것이다.
eigenvalue decomposition의 결과로 일반적인 skew-symmetric 행렬의 block decomposition을 scale까지 생성할 수 있다. 따라서 를 다음과 같이 작성할 수 있다.
여기서 는 어떤 orthogonal 행렬이다. 그러므로 decomposition을 다음과 같이 재작성할 수 있다.
이 표현식을 조심스럽게 살피면, Singular Value Decomposition 과 밀접하게 유사함을 볼 수 있다. 여기서 는 2개의 동일한 singular 값을 포함한다. 를 scale까지 알고 형식을 취한다고 가정하면, 다음과 같은 의 분해에 도달한다.
주어진 분해가 유효함을 검사를 통해 증명할 수 있고 또한 다른 분해가 없음을 증명할 수 있다. 의 형식은 그 left null space가 의 null space와 동일해야 한다는 사실에 의해 결정된다. unitray 행렬 와 가 주어지면 임의의 rotation 은 으로 decompose 될 수 있다. 여기서 는 또 다른 rotation 행렬이다. 이 값들을 대입하면 scale까지 가 된다. 따라서 는 나 과 일치해야 한다.
의 분해가 행렬 나 가 직교한다는 것만 보장한다. 이 유효한 rotation이라는 것을 보장하려면 단순히 의 행렬식이 양수임을 확인하면 된다.
rotation 이 잠재적인 2개의 값을 취할 수 있는 것과 유사하게 translation 벡터 도 여러 값을 취할 수 있다. cross product의 정의에서 다음을 알 수 있다.
가 unitary라는 것을 알면, 임을 알 수 있다. 그러므로 이 분해에서 에 대한 추정치는 위의 방정식과 가 scale까지 알려져 있다는 사실로부터, 다음을 의미한다.
여기서 은 의 3번째 행이다. 검사에 의해 를 벡터 로 부호까지 재형식화하여 동일한 결과를 얻을 수 있다는 것을 확인할 수도 있다.
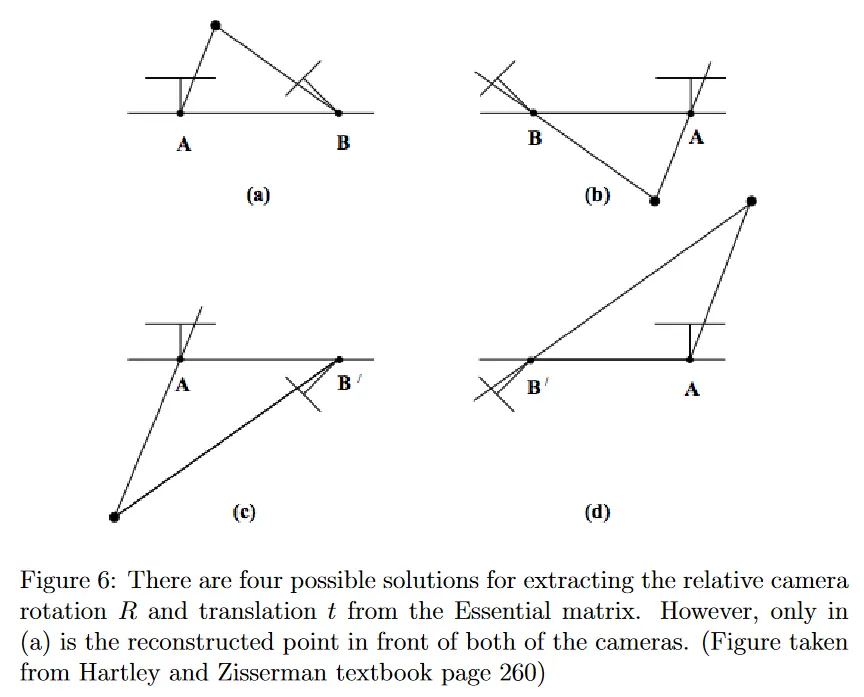
그림 6에 나온대로, 과 모두에 대해 각각 2가지 옵션이 존재하기 때문에 잠재적인 4개의 쌍이 존재한다. 직관적으로 4개 쌍은 특정한 방향에서 카메라를 회전시키거나 반대 방향에서 카메라를 회전시키는 모든 가능한 쌍과 특정한 방향 또는 반대 방향으로 translating 하는 옵션을 결합한 것을 포함한다. 그러므로 이상적인 조건하에 올바른 쌍을 결정하기 위해 단 한 점만 triangulate하면 된다. 올바른 쌍에 대해 triangulated 점 는 두 카메라의 앞에 존재하며, 이것은 두 카메라 reference system 측면에서 양의 -좌표를 갖는다는 것을 의미한다. 측정 노이즈 때문에 우리는 종종 단일 점만으로 triangulating 하지 않고 대신 많은 점을 triangulate 하고 두 카메라 앞에 가장 많은 점을 포함하는 쌍을 올바른 쌍으로 결정한다.
5 An example structure from motion pipeline
상대적인 motion 행렬 을 발견한 후에 이를 사용하여 점 의 월드 좌표를 결정할 수 있다. 대수적 방법의 경우, 그런 점의 추정치는 perspective 변환 까지 정확하다. Essential 행렬에서 카메라 행렬을 추출할 때 추정치는 scale까지만 알 수 있다. 두 경우 모두 앞서 설명한 triangulartion 방법을 통해 추정된 카메라 행렬에서 3d 점을 계산할 수 있다.
multi-view 경우에 대한 확장은 쌍별 카메라를 연결하여 수행될 수 있다. 대응점이 충분하면 대수적 접근 또는 Essential 행렬을 사용하여 임의의 카메라 행렬에 3d 점의 해를 얻을 수 있다. 재구성된 3d 점은 카메라 쌍 사이에서 사용 가능한 대응점과 연관된다. 이러한 쌍별 해는 다음에 보게 될 bundle adjustment이라는 접근법으로 결합(최적화) 할 수 있다.
5.1 Bundle adjustment
지금까지 논의한 structure from motion 문제를 해결하기 위한 이전 방법들에는 주요한 한계가 존재한다. factorization 방법은 모든 점이 모든 이미지에서 visible이라고 가정한다. 이것은 occlusion이나 대응점 찾기 실패 때문에 이미지가 많거나 멀리 떨어져 촬영된 경우 일어날 가능성이 매우 없다. 마지막으로 대수적 접근은 카메라 체인으로 결합할 수 있는 쌍별 해를 생성하지만 모든 카메라와 3d 점을 사용하여 coherent(일관된) 최적화 재구성을 해결하지 않는다.
이러한 한계를 해결하기 위해 bundle adjustment를 소개한다. 이것은 structure from motion 문제를 해결하기 위한 비선형 방법이다. 최적화에서 우리는 reprojection error를 최소화하는데 초점을 맞춘다. 이것은 재구성된 점을 추정된 카메라로 projection할 때와 모든 카메라와 모든 점에 대한 대응 관측치 사이의 픽셀 거리를 의미한다. 이전에 triangulation을 위한 비선형 최적화 방법을 논의할 때 주로 2대 카메라 경우에 초점을 맞추었는데, 여기서는 자연스럽게 각 카메라가 두 카메라 사이의 모든 대응점을 보는 것으로 가정했다. 그러나 bundle adjustment는 여러 카메라를 다루므로 각 카메라가 볼 수 있는 관찰에 대해서만 reprojection error를 계산한다. 그렇지만 궁극적으로 이 최적화 방법은 triangulation에 대한 비선형 방법을 논의할 때 소개된 것과 매우 유사하다.
bundle adjustment의 비선형 최적화를 해결하기 위한 두 가지 일반적인 접근은 Gauss-Newton algorithm과 Levenberg-Marquardt algorithm이다. Gauss-Newton algorithm에 대해서는 이전 섹션에서 상세한 내용을 찾을 수 있고 Levenberg-Marquardt algorithm에 대해서는 Hartley와 Zisserman 교재에서 상세한 내용을 찾을 수 있다.
결론적으로 bundle adjustment는 우리가 조사한 다른 방법과 비교하여 중요한 이점과 한계를 갖는다. 이것은 많은 수의 view를 smoothly 다룰 수 있고 특정한 점이 모든 이미지에서 관찰되지 않은 경우도 다룰 수 있다는 점에서 특히 유용하다. 그러나 주요한 한계는 파라미터가 view의 수에 따라 증가함에 하므로 특히 큰 최소화 문제라는 것이다. 또한 이것은 비선형 최적화 기법에 의존하기 때문에 좋은 초기화 조건이 필요하다. 이러한 이유로 bundle adjustment는 종종 structure from motion 구현에서 마지막 단계로 사용되는 경우가 많다(즉 factorization 또는 algebraic 접근 이후에). factorization 또는 algebraic 접근이 최적화 문제에 대한 좋은 초기 해를 제공할 수 있기 때문이다.