Search
Duplicate

AI/ Normalizing Flow

Normalizing Flow

Normalizing flow는 Evidence Lower Bound(ELBO)를 사용하는 VAE나 Discriminator-Generator의 GAN과는 완전히 다른 생성 모델이다. Normalizing Flow는 Change of Variables를 이용하여 단순한 분포(일반적으로 가우시안)에서 복잡한 분포(최종적으로 생성하려는)로 직접 변환하여 데이터를 생성한다.
여기서 데이터 분포를 변환한다는 것은 데이터를 변환한다는 것이 아니라 데이터가 존재하는 벡터 공간을 변환한다는 이야기다. 원본 데이터가 존재하는 벡터 공간을 데이터를 다루기 쉬운의 벡터 공간으로 변환하는데, 이때 벡터 공간을 선형으로 변환 가능하면 단순히 행렬 곱으로 가능하지만, 복잡한 데이터 분포는 선형으로 변환이 안되기 때문에 비선형 변환을 해야 한다. 또한 데이터를 생성하려면 변환 된 벡터 공간에서 샘플링 한 데이터를 다시 원본 데이터가 존재하는 벡터 공간으로 역 변환을 해야 하는데, normalizing flow는 바로 그 역변환을 학습하는 모델에 해당한다. 비슷한 개념이 diffusion 모델에도 적용되지만, diffusion model은 noise를 더하고 빼는 방법을 사용하므로 invertible이라는 제약 조건이 없다. 한편 autoencoder 류의 모델은 벡터 공간을 변환하는 것과 달리 데이터를 (일반적으로 저 차원인) 다른 벡터 공간에 투영(projection)하는 것에 기반한 방법이라 할 수 있다.
normalizing flows는 단순한 base 분포(일반적으로 가우시안) p(u)p(\bold{u})에서 뽑은 확률 변수 u∈RD\bold{u} \in \mathbb{R}^D를 비선형이지만 가역인 변형 f:RD→RD\bold{f}:\mathbb{R}^D \to \mathbb{R}^D에 전달하여 복잡한 확률 분포 p(x)p(\bold{x})를 생성한다. 즉 p(x)p(\bold{x})는 다음 프로세스에 의해 정의된다.
x=f(u)u∼p(u)\bold{x} = \bold{f}(\bold{u}) \\ \bold{u} \sim p(\bold{u})
기본 분포가 단순하더라도 충분히 유연한 변환 f\bold{f}을 사용하면 변형된 변수 x\bold{x}에 대한 복잡한 분포를 유도할 수 있다.
p(x)p(\bold{x})에서 샘플링하는 것은 간단하다. 먼저 단순한 분포 p(u)p(\bold{u})에서 u\bold{u}를 샘플한 다음 변환 함수 x=f(u)\bold{x} = f(\bold{u})를 계산하면 된다. normalizing flow에서는 기본 분포에서 복잡한 분포로 변환하는 것을 forward 변환이라고 한다.
p(x)p(\bold{x})를 계산하기 위해 f\bold{f}가 가역이라는 사실을 이용한다. 복잡한 분포를 base 분포에 다시 매핑하여 ‘normalizes’하는 역 매핑을 g(x)=f−1(x)=u\bold{g}(\bold{x}) = \bold{f}^{-1}(\bold{x}) = \bold{u}라 한다. (실제 모델에서 역 매핑은 모델의 성능을 평가하는 용도로 사용되며, 기본적인 훈련과 샘플링에서 필수적인 단계는 아님) change-of-variables 공식을 사용하여 다음을 얻을 수 있다.
px(x)=pu(g(x))∣det⁡J(g)(x)∣=pu(u)∣det⁡J(f)(u)∣−1p_x(\bold{x}) = p_u(\bold{g}(\bold{x}))|\det \bold{J}(\bold{g})(\bold{x})| = p_u(\bold{u})|\det \bold{J}(\bold{f})(\bold{u})|^{-1}
여기서 J(f)(u)=∂f∂u∣u\bold{J}(\bold{f})(\bold{u}) = {\partial \bold{f} \over \partial \bold{u}}|_\bold{u}는 u\bold{u}에서 평가된 f\bold{f}의 야코비안 행렬이다. 위 식의 양변에 log를 취하여 다음을 얻는다.
log⁡px(x)=log⁡pu(u)−log⁡∣det⁡J(f)(u)∣\log p_x(\bold{x}) = \log p_u(\bold{u}) - \log |\det \bold{J}(\bold{f})(\bold{u})|
단순한 분포에서 원하는 수준의 복잡한 분포로 한 번에 변환할 수 없기 때문에 chain 형식으로 여러 매핑을 연결하여 점점 더 복잡한 분포로 변환하는 방식을 사용한다. (이러한 방식은 이후 diffusion model로 이어진다.)
이것은 다음과 같은 함수 합성으로 구성할 수 있다.
f=fN∘...∘f1\bold{f} = \bold{f}_N \circ ... \circ \bold{f}_1
f\bold{f}가 가역이므로 이에 대한 역도 다음처럼 구성된다.
g=g1∘...∘gN\bold{g} = \bold{g}_1 \circ ... \circ \bold{g}_N
이에 대한 log 야코비안 행렬식은 다음과 같이 주어진다.
log⁡∣det⁡J(g)(x)∣=∑i=1Nlog⁡∣det⁡J(gi)(ui)∣\log |\det \bold{J}(\bold{g})(\bold{x})| = \sum_{i=1}^N \log |\det \bold{J}(\bold{g}_i)(\bold{u}_i)|
확률 변수가 통과하는 경로를 flow라 하고 연속 분포에 의해 형성된 전체 체인을 normalizing flow라고 부른다. 방정식에서 계산에 필요한 변환 함수는 다음 두 가지 속성을 만족해야 한다.
1.
쉽게 가역이어야 한다.
2.
야코비안 행렬식을 쉽게 계산할 수 있어야 한다.

Affine Flow

normalizing flow는 역함수를 위해 역행렬을 계산해야 하는데, 가장 단순한 선택은 scale-and-shift인 affine 변환 x=f(u)=Au+b\bold{x} = \bold{f}(\bold{u}) = \bold{Au} + \bold{b}을 사용하는 것이다. 여기서 A\bold{A}가 가역 정사각 행렬이면 전단사이고 그 역도 성립한다. f\bold{f}의 야코비안 행렬식은 det⁡A\det\bold{A}이고 역은 u=f−1(x)=A−1(x−b)\bold{u} = \bold{f}^{-1}(\bold{x}) = \bold{A}^{-1}(\bold{x}-\bold{b})이다.
affine 전단사를 이용한 flow 구성을 affine flow라 하는데, 이것은 그 자체로 표현력의 한계가 있다.

Elementwise Flow

스칼라값 전단사 h:R→Rh : \mathbb{R} \to \mathbb{R} 를 요소별로 적용하여 가역인 벡터값 전단사 f:RD→RD\bold{f} : \mathbb{R}^D \to \mathbb{R}^D를 생성할 수 있다. 즉 f(u)=(h(u1),..,h(uD))\bold{f}(\bold{u}) = (h(u_1),..,h(u_D)). 함수 f\bold{f}는 가역이고 야코비안 행렬식은 ∏i=1Ddhdui\prod_{i=1}^D {dh \over du_i}로 주어진다. 이런 전단사로 구성된 flow를 elementwise flow라 한다.
elementwise flow 요소 사이의 의존성을 모델링하지 않기 때문에 한계가 있다, 다만 coupling flow 같은 flow의 빌딩 블록으로 사용될 수 있다.

Coupling flow

coupling flow는 입력을 두 부분으로 분할한 후에 한 부분은 원본을 coupling layer라 불리는 layer를 통과 시켜 scale과 translation 값을 얻고, 그것을 이용해서 나머지 부분을 scale-shift 하는 방법을 사용한다. 이 방법을 사용하면 차원 사이의 의존성을 모델링할 수 있다.
보다 형식적으로 입력 u∈RD\bold{u} \in \mathbb{R}^D을 두 부분 집합 (uA,uB)∈Rd×RD−d(\bold{u}^A,\bold{u}^B) \in \mathbb{R}^d \times \mathbb{R}^{D-d}으로 분할한다. 여기서 dd는 11과 D−1D-1 사이의 정수이다. 전단사 f^(⋅;θ):Rd→Rd\hat{\bold{f}}(\cdot;\boldsymbol{\theta}) : \mathbb{R}^d \to \mathbb{R}^d가 θ\boldsymbol{\theta}에 의해 파라미터화되고 부분공간 Rd\mathbb{R}^d에 작용한다고 가정한다. f:RD→RD\bold{f} : \mathbb{R}^D \to \mathbb{R}^D가 주어지면 함수 x=f(u)\bold{x} = \bold{f}(\bold{u})를 다음처럼 정의한다.
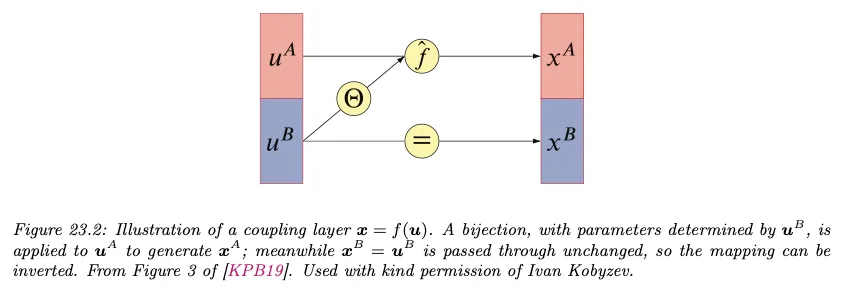
xA=f^(uA;Θ(uB))xB=uB\begin{aligned} \bold{x}^A &= \hat{\bold{f}}(\bold{u}^A;\Theta(\bold{u}^B)) \\ \bold{x}^B &= \bold{u}^B \end{aligned}
여기서 Θ\Theta는 conditioner라고 부르는 임의의 함수로 종종 심층 신경망으로 구현된다. f^\hat{\bold{f}}와 Θ\Theta를 통해 uA\bold{u}^A와 uB\bold{u}^B를 함께 결합하기 때문에 함수 f\bold{f}를 coupling layer라고 부른다. 아래 그림 참조.
커플링 레이어 f\bold{f}는 가역이고 역은 u=f−1(x)\bold{u} = \bold{f}^{-1}(\bold{x})로 주어진다. 여기서
uA=f^−1(xA;Θ(xB))uB=xB\begin{aligned} \bold{u}^A &= \hat{\bold{f}}^{-1}(\bold{x}^A;\Theta(\bold{x}^B)) \\ \bold{u}^B &= \bold{x}^B \end{aligned}
즉 f−1\bold{f}^{-1}은 단순히 f^\hat{\bold{f}}를 f^−1\hat{\bold{f}}^{-1}와 교체하여 주어진다. 이렇게 다소 이상해 보이는 식을 사용하는 이유는 f\bold{f}의 야코비안을 삼각행렬로 만들기 위함이다. xB\bold{x}^B가 uA\bold{u}^A에 의존하지 않기 때문에 f\bold{f}의 야코비안은 다음과 같은 block triangular이 된다. 따라서 J(f)\bold{J}(\bold{f})는 J(f^)\bold{J}(\hat{\bold{f}})와 동등하다.
J(f)=(∂xA/∂uA∂xA/∂uB∂xB/∂uA∂xB/∂uB)=(J(f^)∂xA/∂uB0I)\bold{J}(\bold{f}) = \begin{pmatrix}\partial\bold{x}^A/\partial\bold{u}^A & \partial\bold{x}^A/\partial\bold{u}^B \\ \partial\bold{x}^B/\partial\bold{u}^A & \partial\bold{x}^B/\partial\bold{u}^B \end{pmatrix} = \begin{pmatrix} \bold{J}(\hat{\bold{f}}) & \partial\bold{x}^A/\partial\bold{u}^B \\ \bold{0} & \bold{I} \end{pmatrix}
f\bold{f}의 야코비안이 삼각행렬이 되기 때문에 f\bold{f}의 야코비안의 행렬식은 대각 성분의 곱으로 표현된다. RealNVP와 같은 모델은 f^\hat{\bold{f}}를 exp()를 씌운 scale과 translation의 합 xA=uA∗exp⁡(scale)+translation\bold{x}^A = \bold{u}^A * \exp(\text{scale}) + \text{translation}으로 표현하는데, 이 경우 f^\hat{\bold{f}}의 야코비안의 대각성분은 exp(scale)이 되며, 해당 야코비안의 행렬식은 결국 exp(scale)의 합이 된다. log 행렬식을 구하면 더 단순하게 scale의 합이 된다.
coupling layer는 입력을 반으로 나눈 것 중 하나에 대해서만 업데이트가 되기 때문에, coupling layer를 여러 층 쌓고, 각 레이어에서 교차로 업데이트하여 모든 입력이 반영될 수 있도록 한다.

Autoregressive flows

normalizing flow의 flow 변환을 autoregressive model로 구성하는 경우 autoregressive flow라고 한다.
예컨대 입력 u\bold{u}가 DD개 스칼라 요소를 포함한다고 가정하자. 즉 u=(u1,...,uD)∈RD\bold{u} =(u_1,...,u_D) \in \mathbb{R}^D. autoregressive 전단사를 f:RD→RD\bold{f} : \mathbb{R}^D \to \mathbb{R}^D로 정의한다. 출력은 다음과 같이 x=(x1,...,xD)∈RD\bold{x} = (x_1,...,x_D) \in \mathbb{R}^D로 표기된다.
xi=h(ui;Θi(x1:i−1))i=1,...,Dx_i = h(u_i;\Theta_i(\bold{x}_{1:i-1})) \\ i = 1,..., D
각 출력 xix_i는 해당하는 입력 uiu_i과 모든 이전 출력 x1:i−1=(x1,...,xi−1)\bold{x}_{1:i-1} = (x_1,...,x_{i-1})에 의존한다. 함수 h(⋅;θ):R→Rh(\cdot;\boldsymbol{\theta}) : \mathbb{R} \to \mathbb{R}는 θ\boldsymbol{\theta}에 의해 파라미터화 되는 스칼라 전단사이고, 함수 Θi\Theta_i는 모든 이전 출력 x1:i−1\bold{x}_{1:i-1}이 주어지면 xix_i를 산출하는 파라미터 θi\boldsymbol{\theta}_i를 출력하는 conditioner이다. coupling flow와 유사하게 Θi\Theta_i는 임의의 비선형 함수일 수 있고 종종 심층 신경망으로 파라미터화 된다.
hh가 가역이기 때문에 f\bold{f} 또한 가역이고 역은 다음과 같이 주어진다.
ui=h−1(xi;Θi(x1:i−1))i=1,...,Du_i = h^{-1}(x_i;\Theta_i(\bold{x}_{1:i-1})) \\ i=1,...,D
f\bold{f}의 중요한 속성은 각 출력 xi\bold{x}_i가 u1:i=(u1,...,ui)\bold{u}_{1:i} = (u_1,...,u_i)에 의존하지만 ui+1:D=(ui+1,...,uD)\bold{u}_{i+1:D} = (u_{i+1},...,u_D)에는 의존하지 않는다는 것이다. 결과적으로 편도함수 ∂xi/∂uj\partial x_i/\partial u_j는 j>ij> i일때 마다 0이다. 따라서 야코비안 행렬 J(f)\bold{J}(\bold{f})은 삼각이고 행렬식은 단순히 대각 성분의 곱이 된다.
det⁡J(f)=∏i=1D∂xi∂ui=∏i=1Ddhdui\det \bold{J}(\bold{f}) = \prod_{i=1}^D {\partial x_i \over \partial u_i} = \prod_{i=1}^D {dh \over du_i}
가역임에도 autoregressive 전단사는 계산적으로 비대칭이다. f\bold{f}를 평가하는 것은 본질적으로 순차적인 반면 f−1\bold{f}^{-1}는 본질적으로 병렬이기 때문이다.

Sample Code

Model

Normalizing Flow 모델의 핵심 building block인 AffineCoupling은 다음과 같이 구성한다.
class AffineCoupling(nn.Module): def __init__(self, in_dim): super(AffineCoupling, self).__init__() self.net = nn.Sequential( nn.Linear(in_dim // 2, 256), nn.ReLU(), nn.Linear(256, 256), nn.ReLU(), nn.Linear(256, in_dim), ) # 단순한 분포를 복잡한 분포로 만드는 forward process def forward(self, x): x1, x2 = x.chunk(2, dim=1) # 입력을 둘로 쪼갬 # scale과 translation는 별도의 layer를 통과하도록 할 수도 있지만 그 둘이 결국 동일한 구조이기 때문에 같은 layer를 통과시킨 후 쪼갠다. scale, translation = self.net(x2).chunk(2, dim=1) scale = torch.tanh(scale) # 안정적인 학습을 위해 tanh 사용 # RealNVP 방식대로 scale을 exp()하여 입력과 요소별 곱하고 translation을 더해서 affine transform을 수행한다. y1 = x1 * torch.exp(scale) + translation y2 = x2 # x2는 원본을 그대로 보낸다. # coupling layer의 야코비안의 행렬식은 대각성분의 곱으로 주어진다. # y1 = x1 * exp(scale) + translation 에 대한 야코비안을 구하면 그것의 대각성분은 exp(scale) 값이 된다. # log det를 구하는 것이므로 log()를 씌워 최종적으로 scale의 합을 구하면 log det가 된다. log_det = scale.log().sum(dim=1) # 다음 레이어에서 x1, x2를 교차하기 위해 [y2, y1]으로 연결한다. return torch.cat([y2, y1], dim=1), log_det # 복잡한 분포를 단순한 분포로 만드는 inverse process # inverse()는 모델의 성능을 평가하는 용도로 사용되며, 기본적인 훈련과 샘플링에서 필수적인 단계는 아님. def inverse(self, y): y1, y2 = y.chunk(2, dim=1) scale, translation = self.net(y2).chunk(2, dim=1) scale = torch.tanh(scale) x1 = (y1 - translation) / torch.exp(scale) x2 = y2 return torch.cat([x2, x1], dim=1)
Python
복사
affine coupling layer를 여러 층 쌓아서 Normalizing flow 모델을 구성한다.
class NormalizingFlow(nn.Module): def __init__(self, dim, n_flows): super(NormalizingFlow, self).__init__() # flows를 여러 층 쌓는다. self.flows = nn.ModuleList([AffineCoupling(dim) for _ in range(n_flows)]) def forward(self, x): log_det_J = 0 for flow in self.flows: x, log_det = flow(x) log_det_J += log_det # Accumulate log determinant return x, log_det_J
Python
복사

Objective

Normalizing flow의 loss 함수
# 손실 함수 def loss_function(base_distribution, x, log_det_J): # 이것은 normalizing flow의 핵심인 p_x(x) = p_u(u)|det J(f)(u)|^{-1}에 해당한다. # log를 취했기 때문에 p_u(u)와 |det J|의 곱이 아니라 합으로 표현됨. log_prob = base_distribution.log_prob(x) + log_det_J return -torch.mean(log_prob) # Negative log-likelihood loss
Python
복사

Train

모델 학습
# 데이터 생성을 위한 기본 분포 설정 base_distribution = dist.Independent(dist.Normal(torch.zeros(2), torch.ones(2)), 1) # 데이터 샘플 생성 함수 def sample_data(batch_size=512): z = base_distribution.sample((batch_size,)) return z # 모델, 옵티마이저 설정 dim = 2 n_flows = 6 model = NormalizingFlow(dim, n_flows) optimizer = optim.Adam(model.parameters(), lr=0.001) # 훈련 함수 정의 def train(model, optimizer, epochs=1000, batch_size=512): model.train() for epoch in range(epochs): z = sample_data(batch_size) optimizer.zero_grad() x, log_det_J = model(z) loss = loss_function(base_distribution, x, log_det_J) loss.backward() optimizer.step() if epoch % 100 == 0: print(f'Epoch {epoch} Loss: {loss.item()}') # 모델 학습 실행 train(model, optimizer) # 샘플 생성 후 확인 # 모델 평가 시 역변환 사용 예제 model.eval() with torch.no_grad(): # 샘플 데이터 생성 z = sample_data(5) # 순방향 변환으로 샘플 생성 transformed_samples, _ = model(z) # 역변환 수행 original_samples = [flow.inverse(y) for flow, y in zip(reversed(model.flows), reversed(transformed_samples))] print("Transformed Samples:") print(transformed_samples) print("Original Samples after Inverse Transformation:") print(original_samples)
Python
복사

참고

Made with