Search
Duplicate

AI/ Article/ Generative Modeling by Estimating Gradients of the Data Distribution

Generative Modeling by Estimating Gradients of the Data Distribution | Yang Song
This blog post focuses on a promising new direction for generative modeling. We can learn score functions (gradients of log probability density functions) on a large number of noise-perturbed data distributions, then generate samples with Langevin-type sampling. The resulting generative models, often called <em>score-based generative models</em>, has several important advantages over existing model families: GAN-level sample quality without adversarial training, flexible model architectures, exact log-likelihood computation, and inverse problem solving without re-training models. In this blog post, we will show you in more detail the intuition, basic concepts, and potential applications of score-based generative models.
https://yang-song.net/blog/2021/score/

Introduction

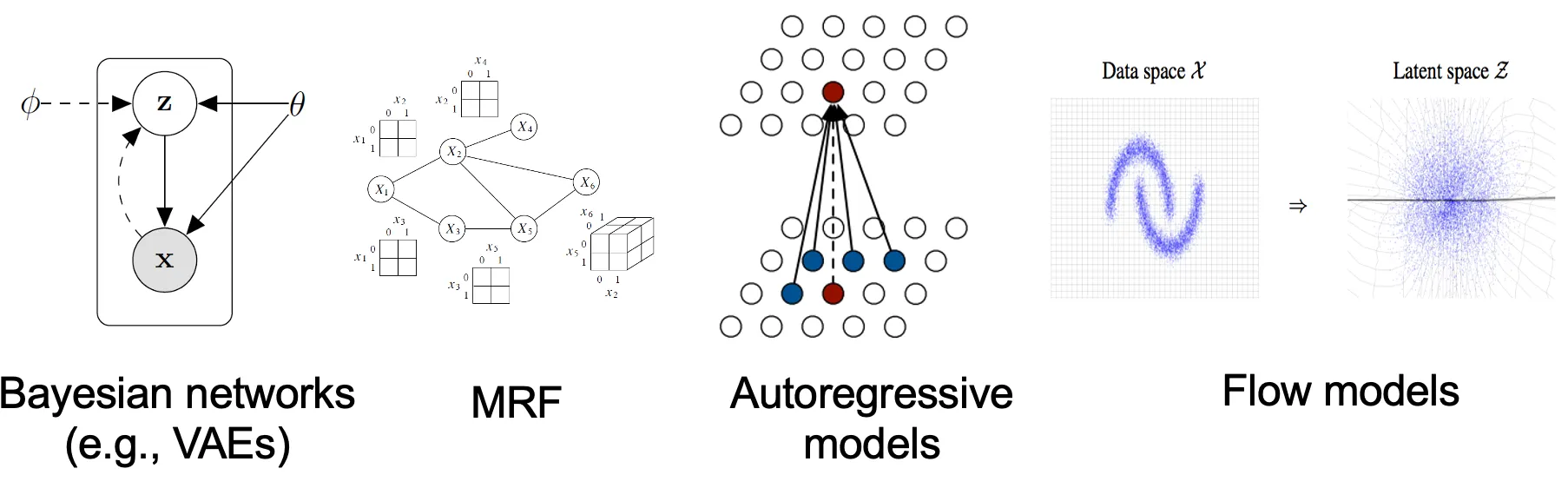
기존의 생성 모델링 기법은 확률 분포를 표현하는 방식에 따라 크게 두 가지로 분류할 수 있다.
1.
likelihood-based models, 이것은 (근사) maximum likliehood를 통해 분포의 확률 밀도(또는 질량) 함수를 직접 학습하는 방법이다. 전형적인 likelihood 기반 모델은 autoregressive models, normalizing flow model, energy-based models(EBMs), variational auto-encoders(VAEs)가 포함된다.
2.
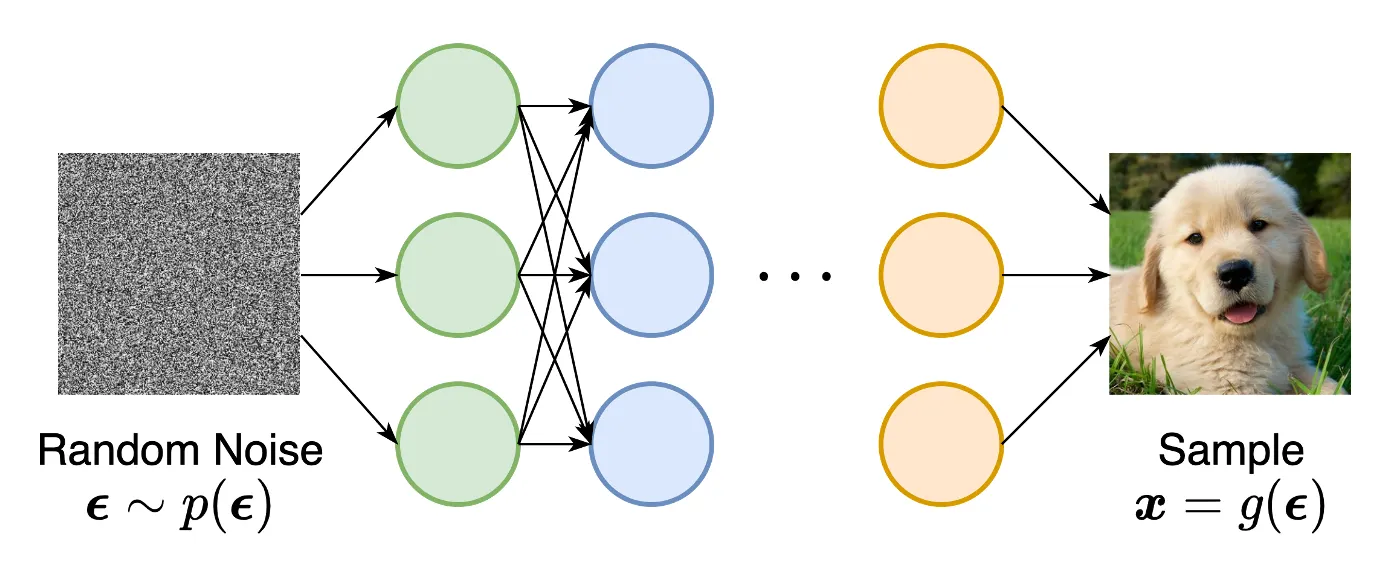
implicit generative models, 여기서 확률 분포는 샘플링 프로세스의 모델로써 암시적으로 표현된다. 가장 prominent(중요한) 예는 Generative Adversarial Networks(GANs)이다. 여기서 랜덤 가우시안 백터를 신경망으로 변환하여 데이터 분포에서 새로운 샘플을 합성한다.
그러나 Likelihood 기반 모델과 암시적 생성 모델 모두 상당한 한계가 있다. Likelihood 기반 모델은 likelihood 계산을 위한 다루기 용이한 normalizing 상수를 보장하기 위해 모델 아키텍쳐에 강한 제약이 필요하거나 maximum likelihood 학습을 근사하는 surrogate 목적에 의존해야 한다. 반면에 암시적 생성 모델은 종종 adversarial 학습을 요구하며 이것은 notoriously(악명 높게) 불안정하고 mode 붕괴로 이어질 수 있다.
이 블로그 포스트에서 이러한 몇 가지 한계를 우회할 수 있는 확률 분포를 나타내는 또 다른 방법을 소개한다. 핵심 아이디어는 log 확률 밀도 함수의 gradient를 모델링하는 것으로 이 수량은 종종 (stein) score function이라 불린다. 이런 score-based 모델은 다루기 용이한 normalizing 상수가 필요하지 않고 score matching을 통해 직접 학습될 수 있다.
score-based 모델은 많은 downstream 작업과 애플리케이션에서 최첨단 성능을 달성했다. 이러한 작업에는 이미지 생성(GAN 보다 낫다!), 오디오 합성, 모양 생성 및 음악 생성이 포함된다. 게다가 score-based 모델은 정규화 흐름 모델과 연결되어 있어서 정확한 likelihood 계산과 representation learning이 가능하다. 추가적으로 모델링과 score 추정은 image inpainting, image colorization, compressive sensing, medical image reconstruction(CT, MRI 같은)과 같은 inverse 문제를 해결을 facilitates(촉진) 한다.

The score function, score-based models, and score matching

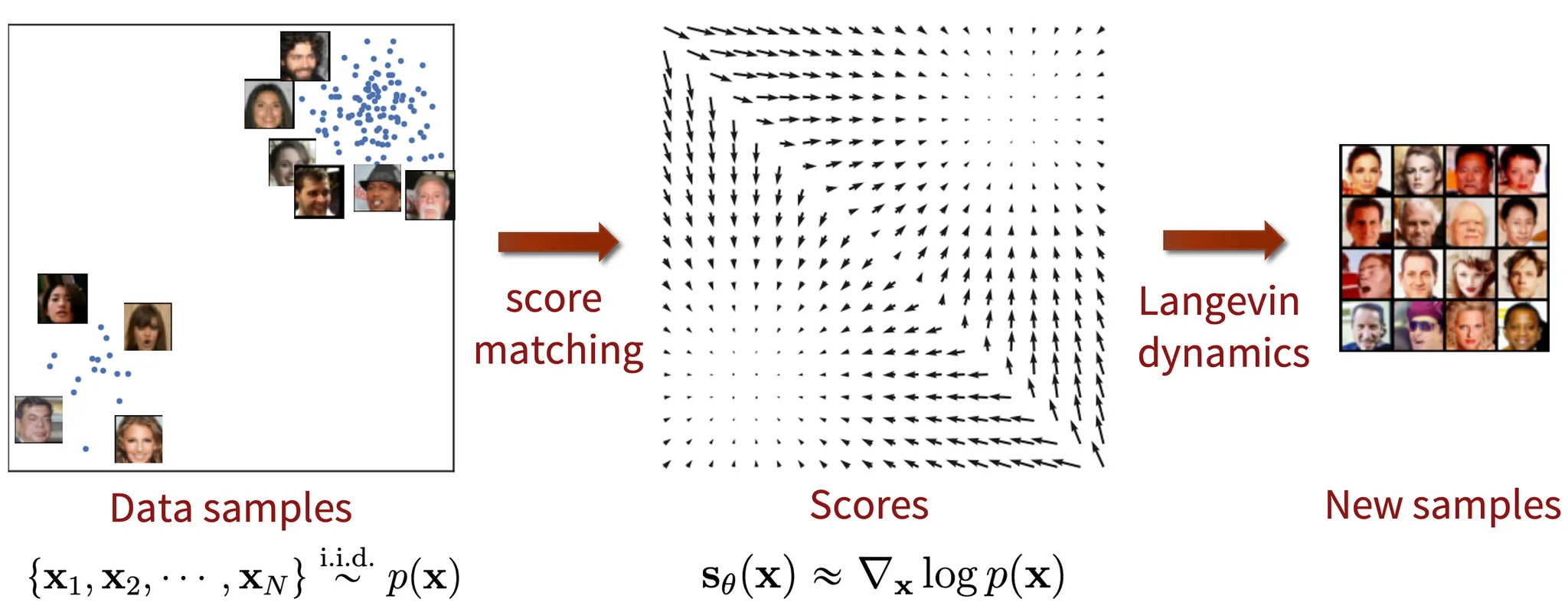
데이터셋 {x1,x2,⋯ ,xN}\{\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_N\}을 가졌다고 가정하자. 여기서 각 포인트는 기본 데이터 분포 p(x)p(\bold{x})에서 독립적으로 뽑힌다. 이 데이터셋이 주어지면 생성 모델링의 목표는 분포에서 샘플링하여 원하는대로 새로운 데이터 포인터를 합성할 수 있는 데이터 분포에 모델을 fit 하는 것이다.
이런 생성 모델을 구축하는 측면에서 우선 확률 분포를 표현하는 방법이 필요하다. likelihood 기반 모델에서 한 가지 방법은 직접적으로 확률 밀도 함수(probability density function, pdf)나 확률 질량 함수(probability mass function, pmf)를 모델링하는 것이다. fθ(x)∈Rf_{\boldsymbol{\theta}}(\mathbf{x}) \in \mathbb{R}를 학습 가능한 파라미터 θ\boldsymbol{\theta}로 파라미터화된 실수값 함수라고 하자. pdf를 다음과 같이 정의할 수 있다.
pθ(x)=e−fθ(x)Zθ(1)p_{\boldsymbol{\theta}}(\mathbf{x}) = \frac{e^{-f_{\boldsymbol{\theta}}(\mathbf{x})}}{Z_{\boldsymbol{\theta}}} \tag{1}
여기서 Zθ>0Z_{\boldsymbol{\theta}} > 0은 ∫pθ(x)dx=1\int p_{\boldsymbol{\theta}}(\bold{x})d\bold{x} = 1과 같은 θ\boldsymbol{\theta}에 의존하는 normalizing 상수이다. 여기서 함수 fθ(x)f_{\boldsymbol{\theta}}(\bold{x})는 종종 unnormalized 확률 모델 또는 energy-based 모델이라 부른다.
데이터의 log-likelihood를 maximizing하여 pθ(x)p_{\boldsymbol{\theta}}(\bold{x})를 학습할 수 있다.
max⁡θ∑i=1Nlog⁡pθ(xi)(2)\max_{\boldsymbol{\theta}} \sum_{i=1}^N \log p_{\boldsymbol{\theta}}(\mathbf{x}_i) \tag{2}
그러나 방정식 (2)는 pθ(x)p_{\boldsymbol{\theta}}(\bold{x})가 normalized 확률 밀도 함수일 것을 요구한다. 이것은 pθ(x)p_{\boldsymbol{\theta}}(\bold{x})을 계산하는 측면에서 바람직하지 않은데, 정규화 상수 ZθZ_{\boldsymbol{\theta}}를 평가해야 하기 때문이다. —이것은 일반적으로 임의의 함수 fθ(x)f_{\boldsymbol{\theta}}(\bold{x})에 대해 다루기 까다로운 수량이다. 따라서 maximum likliehood 학습을 실현가능하게 만들어야 한다. likelihood 기반 모델은 ZθZ_{\boldsymbol{\theta}}를 다루기 용이하게 만들기 위해 모델 아키텍쳐에 제한을 두거나(예: autoregressive 모델에서 causal convolution, normalizing flow 모델에서 가역 네트워크), 계산적으로 비쌀 수 있는 normalizing 상수를 근사해야 한다.(예 VAE에서 variational inference 또는 contrastive divergence에서 사용되는 MCMC 샘플링)
밀도 함수 대신 score 함수를 모델링하여 까다로운 정규화 상수의 어려움을 sidestep(회피)할 수 있다. 분포 p(x)p(\bold{x})의 score function은 다음과 같이 정의된다.
∇xlog⁡p(x)\begin{equation} \nabla_\mathbf{x} \log p(\mathbf{x}) \notag \end{equation}
그리고 score 함수를 위한 모델을 score-based 모델이라 부르고 sθ(x)s_{\boldsymbol{\theta}}(\bold{x})로 표기한다. score-based 모델은 sθ(x)≈∇xlog⁡p(x)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}) \approx \nabla_\mathbf{x} \log p(\mathbf{x}) 같이 학습되고 정규화 상수에 관한 걱정 없이 파라미터화 될 수 있다. 예컨대 방정식 1에서 정의한 energy-based 모델을 사용하여 score 기반 모델을 쉽게 파라미터화 할 수 있다.
sθ(x)=∇xlog⁡pθ(x)=−∇xfθ(x)−∇xlog⁡Zθ⏟=0=−∇xfθ(x)(3)\begin{equation} \mathbf{s}_\theta (\mathbf{x}) = \nabla_{\mathbf{x}} \log p_\theta (\mathbf{x} ) = -\nabla_{\mathbf{x}} f_\theta (\mathbf{x}) - \underbrace{\nabla_\mathbf{x} \log Z_\theta}_{=0} = -\nabla_\mathbf{x} f_\theta(\mathbf{x}) \end{equation} \tag{3}
score 기반 모델 sθ(x)s_{\boldsymbol{\theta}}(\bold{x})이 정규화 상수 ZθZ_{\boldsymbol{\theta}}와 독립임에 유의하라. 이것은 정규화 상수를 다루기 용이하게 만들기 위한 특별한 아키텍쳐가 필요하지 않기 때문에 다루기 쉽게 사용할 수 있는 모델의 계열이 크게 확장된다.
likelihood 기반 모델과 유사하게 score 기반 모델을 다음과 같이 정의되는 모델과 데이터 분포 사이의 Fisher divergence를 최소화하여 학습할 수 있다.
Ep(x)[∥∇xlog⁡p(x)−sθ(x)∥22](5)\begin{equation} \mathbb{E}_{p(\mathbf{x})}[\| \nabla_\mathbf{x} \log p(\mathbf{x}) - \mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}) \|_2^2] \end{equation} \tag{5}
직관적으로 Fisher divergence는 ground-truth 데이터 score와 score 기반 모델 사이의 제곱된 ℓ2\ell_2 거리를 비교한다. 그러나 이 divergence를 직접 계산하는 것은 unknown 데이터 score ∇xlog⁡p(x)\nabla_\mathbf{x} \log p(\mathbf{x})에 접근해야 하기 때문에 실현 불가능하다.
다행히 ground-truth 데이터 score의 지식 없이 Fisher divergence를 최소화하는 score matching이라 불리는 방법의 계열이 존재한다. score matching 목적은 데이터셋에 직접 추정될 수 있고 (정규화 상수가 알려진) likelihood 기반 모델을 학습하기 위한 log-likelihood 목적과 유사한 stochastic gradient descent를 사용하여 최적화 될 수 있다. adversarial 최적화 없이도 score matching 목적을 최소화하여 score 기반 모델을 학습할 수 있다.
게다가 score matching 목적은 considerable(많은) 모델링 유연성을 제공한다. Fisher Divergence 자체는 sθ(x)s_{\boldsymbol{\theta}}(\bold{x})가 어떤 정규화된 분포의 실제 score 함수일 필요가 없다. 단순히 ground-truth 데이터 score와 score-based 모델 사이의 ℓ2\ell_2 거리만 비교하며, sθ(x)s_{\boldsymbol{\theta}}(\bold{x})의 형식에 대한 추가적인 가정이 없다. 사실 score 기반 모델에 대한 유일한 요구사항은 입력과 출력 차원이 동일한 벡터값 함수여야 한다는 것이며 이것은 실제로 쉽게 만족할 수 있다.
간략히 요약하면 자유로운 아키텍쳐의 score 기반 모델을 score matching으로 학습하여 추정될 수 있는 score 함수를 모델링하여 분포를 나타낼 수 있다.

Langevin dynamics

score 기반 모델 sθ(x)≈∇xlog⁡p(x)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}) \approx \nabla_\mathbf{x} \log p(\mathbf{x})을 학습한 후 Lagevin dynamics라 부르는 반복 절차를 사용하여 샘플을 뽑을 수 있다.
랑주뱅 역학은 score 함수 ∇xlog⁡p(x) \nabla_\mathbf{x} \log p(\mathbf{x})만 사용하여 분포 p(x)p(\bold{x})에서 샘플링하는 MCMC 절차를 제공한다. 구체적으로 임의의 prior 분포 에서 chain을 초기화한 다음 다음을 반복한다.
xi+1←xi+ϵ∇xlog⁡p(x)+2ϵ zi,i=0,1,⋯ ,K(6)\mathbf{x}_{i+1} \gets \mathbf{x}_i + \epsilon \nabla_\mathbf{x} \log p(\mathbf{x}) + \sqrt{2\epsilon}~ \mathbf{z}_i, \quad i=0,1,\cdots, K \tag{6}
여기서 zi∼N(0,I)\mathbf{z}_i \sim \mathcal{N}(0, I)이다. ϵ→0\epsilon \to 0과 K→∞K \to \infty일 때 방정식 (6)의 절차에서 얻어진 xK\bold{x}_K는 어떤 regularity 조건 하에 p(x)p(\bold{x})의 샘플로 수렴한다. 실제로 ϵ\epsilon이 충분히 작고 KK가 충분이 크면 에러는 negliible(무시할 만)하다.
랑주뱅 역학은 ∇xlog⁡p(x)\nabla_\mathbf{x} \log p(\mathbf{x})을 통해 p(x)p(\bold{x})에 접근한다. sθ(x)≈∇xlog⁡p(x)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}) \approx \nabla_\mathbf{x} \log p(\mathbf{x})이므로 score 기반 모델 sθ(x)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x})을 방정식 (6)에 연결하여 샘플을 생성할 수 있다.

Naive score-based generative modeling and its pitfalls

지금까지 score matching을 사용하여 score 기반 모델을 학습한 다음 랑주뱅 역학을 통해 샘플을 생성하는 방법에 대해 논의했다. 그러나 이러한 순진한 접근은 실제로는 제한적인 성공만 거두었다. 이전 작업에서 주목 받지 못했던 score matching의 몇 가지 pitfalls(함정)에 관해 논의한다.
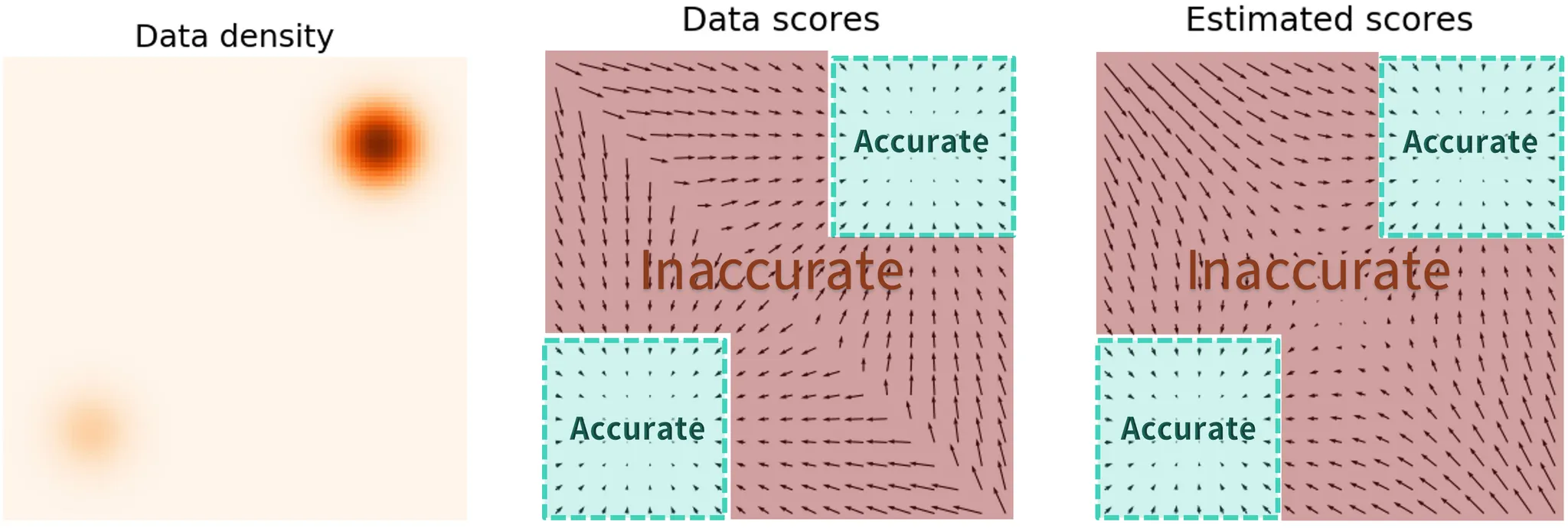
핵심 도전은 score matching 목적을 계산하는데 사용할 수 있는 데이터 포인트가 거의 없는 low density regions에서 추정된 score 함수가 부정확하다는 사실이다. 이것은 score matching이 Fisher divergence를 최소화하기 때문에 예상되는 문제이다.
Ep(x)[∥∇xlog⁡p(x)−sθ(x)∥22]=∫p(x)∥∇xlog⁡p(x)−sθ(x)∥22dx.\mathbb{E}_{p(\mathbf{x})}[\| \nabla_\mathbf{x} \log p(\mathbf{x}) - \mathbf{s}_\theta(\mathbf{x}) \|_2^2] = \int p(\mathbf{x}) \| \nabla_\mathbf{x} \log p(\mathbf{x}) - \mathbf{s}_\theta(\mathbf{x}) \|_2^2 \mathrm{d}\mathbf{x}.
실제 데이터 score 함수와 score 기반 모델 사이의 ℓ2\ell_2 차이가 p(x)p(\bold{x})에 의해 가중치가 부여 되기 때문에 p(x)p(\bold{x})이 작은 low density regions에서 매우 무시된다. 이 동작은 아래 그림과 같은 subpar(수준 이하) 결과를 이끈다.
랑주뱅 역학을 사용하여 샘플링할 때, 데이터가 고차원 공간에 존재할 때 초기 샘플은 low density regions에 있을 가능성이 높다. 따라서 부정확한 score 기반 모델을 사용하연 절차의 시작부터 랑주뱅 역학이 derail(탈선하다), 데이터를 표현하는 높은 품질 샘플을 생성할 수 없게 된다.

Score-based generative modeling with multiple noise perturbations

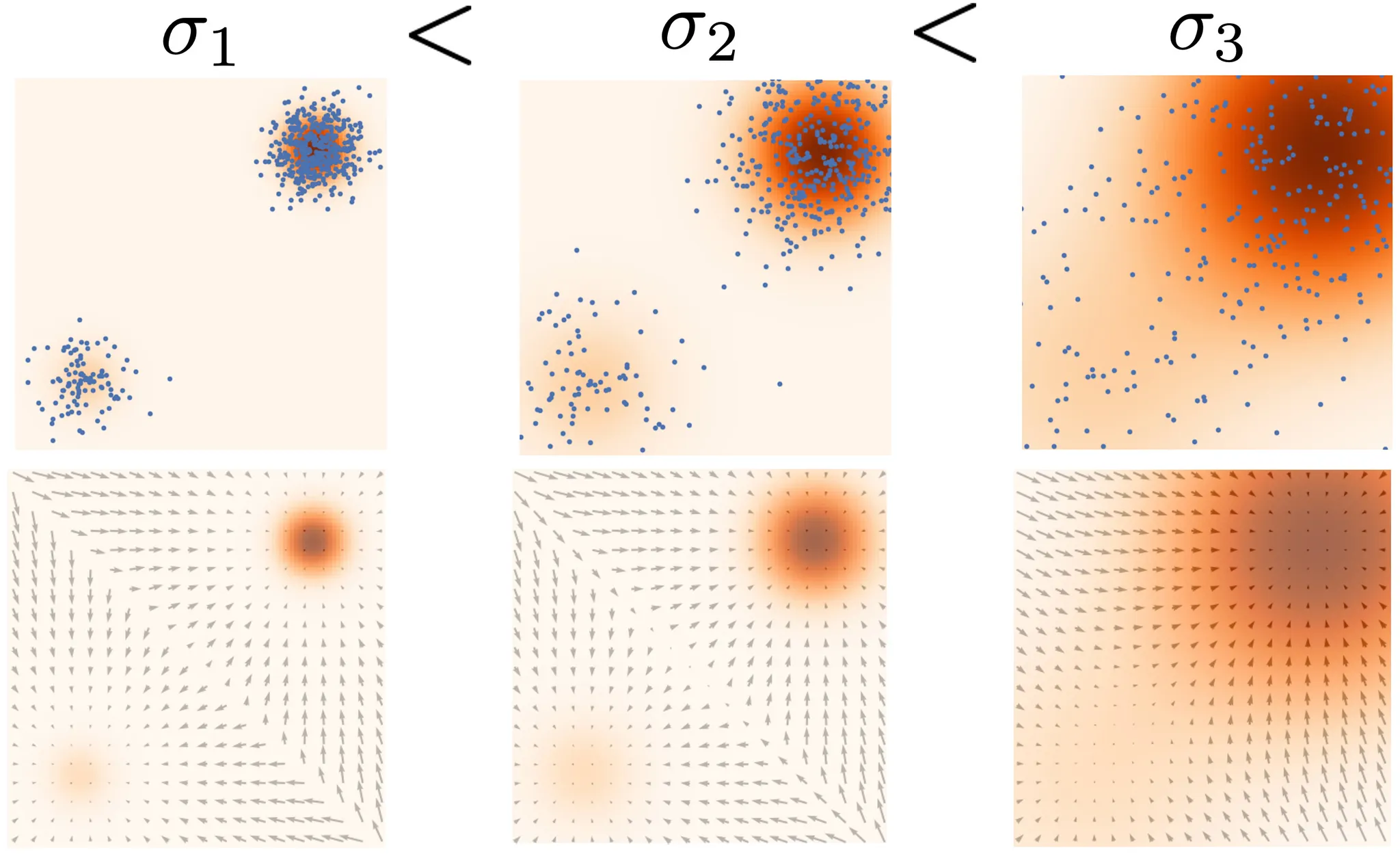
낮은 데이터 밀도의 영역에서 정확한 score 추정의 어려움을 어떻게 우회할 수 있을까? 우리의 해법은 데이터 포인트를 노이즈로 perturb(교란)한 다음 noisy 데이터 포인트에 score 모델을 학습하는 것이다. 노이즈 크기가 충분히 크면 낮은 밀도 영역을 채워서 추정 score의 정확도를 개선할 수 있다. 예컨대 가우시안 노이즈가 추가된 두 가우시안의 혼합을 교란할 때 무슨 일이 벌어지는지를 보여준다.
또 다른 질문이 남아 있다. 교란 절차를 대해 적합한 noise scale을 어떻게 선택할 수 있을까? 노이즈가 클 수록 저밀도 영역을 커버하여 더 나은 score 추정이 가능하지만, 데이터가 over-corrupts 되어 원본 데이터 분포와 크게 달라진다. 반면 노이즈가 작을 수록 원본 데이터 분포를 덜 손상 시키지만 저밀도 영역을 원하는 만큼 커버하지 못한다.
두 경우의 장점을 모두 달성하기 위해, multiple scale의 노이즈 교란을 simultaneously(동시에) 사용한다. 항상 isotropic 가우시안 노이즈를 사용하여 데이터를 교란하고, 총 LL 개의 증가하는 표준 편자 σ1<σ2<...<σL\sigma_1 < \sigma_2 < ... < \sigma_L가 존재한다고 가정하자. 우선 가우시안 노이즈 N(0,σi2I),i=1,2,⋯ ,L\mathcal{N}(0, \sigma_i^2 I), i=1,2,\cdots,L를 사용하여 데이터 분포 p(x)p(\bold{x})를 교란하고 noise-perturbed 분포를 얻는다.
pσi(x)=∫p(y)N(x;y,σi2I)dy.p_{\sigma_i}(\mathbf{x}) = \int p(\mathbf{y}) \mathcal{N}(\mathbf{x}; \mathbf{y}, \sigma_i^2 I) \mathrm{d} \mathbf{y}.
x∼p(x)\mathbf{x} \sim p(\mathbf{x})을 샘플링하고 x+σiz\mathbf{x} + \sigma_i \mathbf{z}를 (여기서 z∼N(0,I)\mathbf{z} \sim \mathcal{N}(0, I)) 계산하여 pσi(x)p_{\sigma_i}(\mathbf{x})에서 쉽게 샘플을 뽑을 수 있다.
다음으로 score matching을 사용하여 Noise Conditional Score-Based Model sθ(x,i)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, i)(신경망으로 파라미터화된 경우 Noise Conditional Score Network(NCSN)이라고도 불린다)을 학습하고, 각 노이즈-교란된 분포의 score 함수 ∇xlog⁡pσi(x)\nabla_\mathbf{x} \log p_{\sigma_i}(\mathbf{x})를 추정한다. 모든 i=1,2,...,Li = 1, 2, ..., L에 대해 sθ(x,i)≈∇xlog⁡pσi(x)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, i) \approx \nabla_\mathbf{x} \log p_{\sigma_i}(\mathbf{x})과 같다.
sθ(x,i)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, i)에 대한 학습 목적은 모든 노이즈 스케일에 대한 Fisher divergence의 weighted sum(가중 합)이다. 특히 다음의 목적을 사용한다.
∑i=1Lλ(i)Epσi(x)[∥∇xlog⁡pσi(x)−sθ(x,i)∥22](7)\begin{equation} \sum_{i=1}^L \lambda(i) \mathbb{E}_{p_{\sigma_i}(\mathbf{x})}[\| \nabla_\mathbf{x} \log p_{\sigma_i}(\mathbf{x}) - \mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, i) \|_2^2] \end{equation} \tag{7}
여기서 λ(i)∈R>0\lambda(i) \in \mathbb{R}_{>0}는 positive weighting 함수이고 종종 λ(i)=σi2\lambda(i) = \sigma_i^2를 선택한다. 목적 (7)은 naive (unconditional) score 기반 모델 sθ(x)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x})을 최적화한 것과 똑같이 score matching을 통해 최적화될 수 있다.
noise-conditional score-based model sθ(x,i)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, i)을 학습한 후에 i=L,L−1,...,1i=L,L-1,...,1의 순서로 랑주뱅 역학을 실행하여 샘플을 생성할 수 있다. 노이즈 스케일 σ1\sigma_1이 시간에 걸쳐 점진적으로 감소 (anneals) 되기 때문에 이 방법을 annealed Langevin dynamics라고 부른다.
여기서 여러 노이즈 스케일을 사용하여 score 기반 생성 모델을 튜닝하기 위한 몇 가지 실용적인 권장사항을 제공한다.
•
σ1<σ2<...<σL\sigma_1 < \sigma_2 < ... < \sigma_L을 geometric progression(등비 수열)로 선택하라. 여기서 σ1\sigma_1은 충분히 작고, σL\sigma_L은 모든 학습 데이터 포인트 사이의 최대 pairwise 거리와 비슷하다. LL 은 일반적으로 수백이나 수천 정도이다.
•
U-Net skip connection을 사용하여 score 기반 모델 sθ(x,i)s_{\theta}(x, i)을 파라미터화 한다.
•
테스트 시 score 기반 모델의 가중치에 exponential moving average를 적용한다.
이런 모범 사례를 통해, 아래와 같이 다양한 데이터 셋에서 GAN과 비슷한 품질의 고품질 이미지 샘플을 생성할 수 있다.

Score-based generative modeling with stochastic differential equations (SDEs)

앞서 논의한 대로, 여러 노이즈 스케일을 추가하는 것이 score 기반 생성 모델의 성공에 핵심이었다. 노이즈 스케일의 수를 무한으로 일반화하여 더 높은 품질의 샘플을 얻을 수 있을 뿐만 아니라 무엇보다도 정확한 log-likelihood 계산과 inverse 문제 해결을 위한 제어 가능한 생성을 얻을 수 있다.
이 introduction에 추가로 Google Colab에 tutorials을 제공한다. (생략)

Perturbing data with an SDE

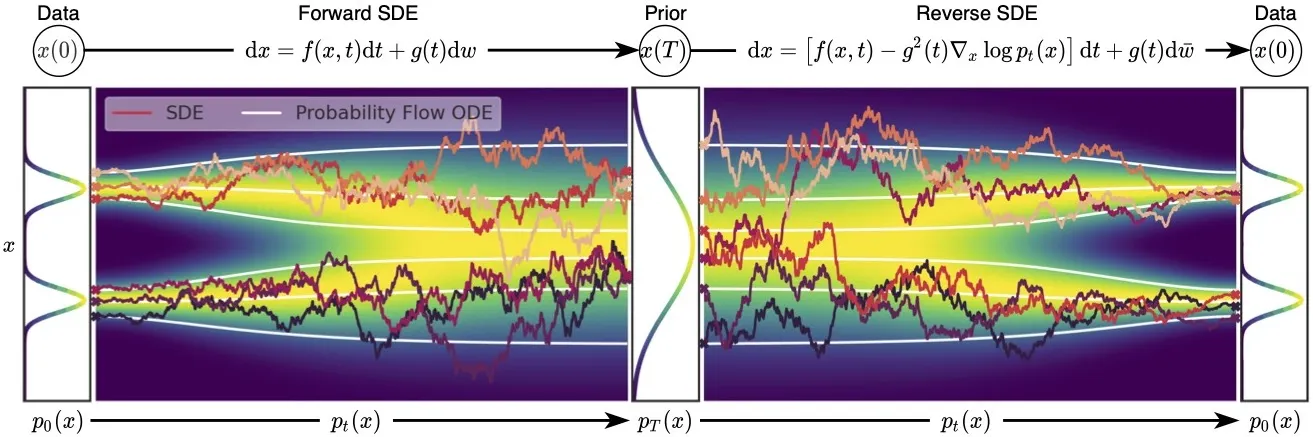
노이즈 스케일의 수가 무한에 가까워지면, 우리는 본질적으로 연속적으로 증가하는 수준의 노이즈로 데이터 분포를 교란한다. 이 경우에 노이즈 교란 절차는 아래 보이는 것과 같은 continuous-time stochastic process가 된다.
어떻게 간결한 방법으로 stochastic process를 표현할 수 있을까? 많은 stochastic process(특히 diffusion processes)는 stochastic differential equations(SDEs)의 해이다. 일반적으로 SDE 프로세스는 다음 형식을 갖는다.
dx=f(x,t)dt+g(t)dw\begin{align} \mathrm{d}\mathbf{x} = \mathbf{f}(\mathbf{x}, t) \mathrm{d}t + g(t) \mathrm{d} \mathbf{w} \tag{8} \end{align}
여기서 f(⋅,t):Rd→Rd\mathbf{f}(\cdot, t): \mathbb{R}^d \to \mathbb{R}^d는 drift coefficient라고 부르는 벡터-값 함수이고 g(t)∈Rg(t) \in \mathbb{R}는 diffusion coefficient라고 부르는 실수값 함수이다. w\bold{w}는 표준 브라운 운동을 나타내고, dw​d\bold{w}​는 극소 white noise라고 볼 수 있다. SDE의 해는 확률 변수 {x(t)}t∈[0,T]\{ \mathbf{x}(t) \}_{t\in [0, T]}의 연속 collection이다. 이 확률 변수는 시간 인덱스 tt가 시작 시간 00에서 종료 시간 TT까지 증가함에 따라 stochastic 궤적을 추적한다. pt(x)p_t(\mathbf{x})를 x(t)\bold{x}(t)의 (marginal) 확률 밀도 함수로 표기하자. 여기서 t∈[0,T]t \in [0, T]는 노이즈 스케일의 수가 유한할 때 i=1,2,...,Li = 1, 2,...,L과 유사하고, pt(x)p_t(\mathbf{x})는 pσi(x)p_{\sigma_i}(\mathbf{x})와 유사하다. t=0t=0에서는 데이터에 교란이 적용되지 않기 때문에 p0(x)=p(x)p_0(\mathbf{x}) = p(\mathbf{x})는 분명히 데이터 분포이다. 충분히 긴 시간 TT에 대해 stochastic 프로레스를 사용하여 p(x)p(\mathbf{x})를 교란한 후에 pT(x)p_T(\mathbf{x})는 prior 분포라 부르는 다루기 쉬운 노이즈 분포 π(x)\pi(\mathbf{x})에 가까워진다. 유한한 노이즈 스케일의 경우에 pT(x)p_T(\mathbf{x})는 pσL(x)p_{\sigma_L}(\mathbf{x})와 유사하며, 이것은 데이터에 가장 큰 노이즈 교란 σL\sigma_L을 적용하는 것에 해당함에 주목한다.
(8)의 SDE은 유한 노이즈 스케일의 경우에 σ1<σ2<⋯<σL\sigma_1 < \sigma_2 < \cdots < \sigma_L을 수동으로 설계한 것과 유사하게 수동으로 설계되었다. 노이즈 교란을 추가하는 방법이 많으며, SDE의 선택은 유니크하지 않다. 예컨대 다음 SDE는
dx=etdw\begin{align} \mathrm{d}\mathbf{x} = e^{t} \mathrm{d} \mathbf{w} \tag{9} \end{align}
평균 0과 지수적으로 증가하는 분산의 가우시안 노이즈를 사용하여 데이터를 교란한다. 이것은 σ1<σ2<...<σL\sigma_{1} < \sigma{2} < ... < \sigma{L}가 geometric progression(등비 수열)일 때 N(0,σ12I),N(0,σ22I),⋯ ,N(0,σL2I)\mathcal{N}(0, \sigma_1^2 I), \mathcal{N}(0, \sigma_2^2 I), \cdots, \mathcal{N}(0, \sigma_L^2 I)를 사용하여 데이터를 교란하는 것과 유사하다. 그러므로 SDE는 {σ1,σ2,...,σL}\{ \sigma_{1}, \sigma{2}, ..., \sigma{L} \}와 같이 모델의 일부로 봐야 한다. [21]에서 이미지에 대해 일반적으로 잘 작동하는 3가지 SDE를 제공한다. Variance Exploding SDE(VE SDE), variance preserving SDE(VP SDE), sub-VP SDE.

Reversing the SDE for sample generation

유한한 수의 노이즈 스케일에서 annealed Langevin dynamics를 사용하여 교란 프로세스를 reversing하여 샘플을 생성할 수 있다. 즉 각 노이즈 교란된 분포에서 랑주뱅 역학을 사용하여 순차적으로 샘플링한다. 무한 노이즈 스케일에 대해 유사하게 reverse SDE를 사용하여 샘플 생성을 위한 교란 프로세스를 reverse 할 수 있다.
중요한 것은 모든 SDE에는 해당하는 reverse SDE가 있다는 것이며, 그것의 닫힌 형식은 다음과 같다.
dx=[f(x,t)−g2(t)∇xlog⁡pt(x)]dt+g(t)dw\begin{equation} \mathrm{d}\mathbf{x} = [\mathbf{f}(\mathbf{x}, t) - g^2(t) \nabla_\mathbf{x} \log p_t(\mathbf{x})]\mathrm{d}t + g(t) \mathrm{d} \mathbf{w} \tag{10} \end{equation}
여기서 SDE (10)이 시간을 거꾸로(t=T→t=0t = T \to t = 0) 풀어야 하기 때문에, dtdt는 음의 infinitesimal(무한소) time step을 나타낸다. reverse SDE를 계산하기 위해 ∇xlog⁡pt(x)\nabla_\mathbf{x} \log p_t(\mathbf{x})를 추정해야 한다. 이것은 정확하게 pt(x)p_t(\mathbf{x})의 score 함수이다.

Estimating the reverse SDE with score-based models and score matching

reverse SDE를 푸는 것은 최종 분포 pT(x)p_T(\bold{x})와 score 함수 ∇xlog⁡pt(x)\nabla_\mathbf{x} \log p_t(\mathbf{x})를 알아야 한다. 설계상 전자는 prior 분포 π(x)\pi(\bold{x})에 가까우며 이것은 완전히 다루기 용이하다. ∇xlog⁡pt(x)\nabla_\mathbf{x} \log p_t(\mathbf{x})를 추정하는 측면에서 Time-Dependent Score-Based Model sθ(x,t)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, t)를 sθ(x,t)≈∇xlog⁡pt(x)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, t) \approx \nabla_\mathbf{x} \log p_t(\mathbf{x})이 되도록 학습한다. 이것은 유한 노이즈 스케일에 대해 사용되는 noise-conditional score-based model sθ(x,i)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, i)을 sθ(x,i)≈∇xlog⁡pσi(x)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, i) \approx \nabla_\mathbf{x} \log p_{\sigma_i}(\mathbf{x})가 되도록 학습하는 것과 유사하다.
sθ(x,t)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, t)에 대한 학습 목적은 다음과 같이 주어지는 Fisher divergence의 continuous weighted combination이다.
Et∈U(0,T)Ept(x)[λ(t)∥∇xlog⁡pt(x)−sθ(x,t)∥22],(11)\begin{equation} \mathbb{E}_{t \in \mathcal{U}(0, T)}\mathbb{E}_{p_t(\mathbf{x})}[\lambda(t) \| \nabla_\mathbf{x} \log p_t(\mathbf{x}) - \mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, t) \|_2^2], \end{equation} \tag{11}
여기서 U(0,T)\mathcal{U}(0, T)는 시간 간격 [0,T][0, T]에 걸쳐 uniform 분포를 나타내고 λ:R→R>0\lambda: \mathbb{R} \to \mathbb{R}_{>0}은 positive weighting 함수이다. 일반적으로 λ(t)∝1/E[∥∇x(t)log⁡p(x(t)∣x(0))∥22]\lambda(t) \propto 1/ \mathbb{E}[\| \nabla_{\mathbf{x}(t)} \log p(\mathbf{x}(t) \mid \mathbf{x}(0))\|_2^2]를 사용하여 시간에 걸쳐 다양한 score matching 손실의 크기를 균형있게 조절한다.
이전과 같이 Fisher divergence의 weighted combination은 denoising score matching과 sliced score matching 같은 score matching 방법을 사용하여 효과적으로 최적화 될 수 있다. 우리의 score 기반 모델 sθ(x,t)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, t)가 최적으로 훈련되면, 이것을 방정식 (10)의 reverse SDE의 표현식에 연결하여 추정된 reverse SDE를 얻을 수 있다.
dx=[f(x,t)−g2(t)sθ(x,t)]dt+g(t)dw\begin{equation} \mathrm{d}\mathbf{x} = [\mathbf{f}(\mathbf{x}, t) - g^2(t) \mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, t)]\mathrm{d}t + g(t) \mathrm{d} \mathbf{w} \tag{12} \end{equation}
x(T)∼π\mathbf{x}(T) \sim \pi에서 시작하고 위의 reverse SDE을 풀어서 샘플 x(0)\mathbf{x}(0)을 얻을 수 있다. 이렇게 얻은 x(0)\mathbf{x}(0)의 분포를 pθp_\theta라 하자. score 기반 모델 sθ(x,t)\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, t)가 잘 학습되면 pθ≈p0p_\theta \approx p_0를 갖는다. 이 경우 x(0)\mathbf{x}(0)는 데이터 분포 p0p_0에서 근사된 샘플이다.
λ(t)=g2(t)\lambda(t) = g^{2}(t)일 때, 일부 regularity 조건 하에 Fisher divergence의 weighted combination과 p0p_0에서 pθp_\theta까지의 KL divergence 사이에 중요한 연결이 존재한다.
KL⁡(p0(x)∥pθ(x))≤T2Et∈U(0,T)Ept(x)[λ(t)∥∇xlog⁡pt(x)−sθ(x,t)∥22]+KL⁡(pT∥π)\begin{equation} \operatorname{KL}(p_0(\mathbf{x})\|p_\theta(\mathbf{x})) \leq \frac{T}{2}\mathbb{E}_{t \in \mathcal{U}(0, T)}\mathbb{E}_{p_t(\mathbf{x})}[\lambda(t) \| \nabla_\mathbf{x} \log p_t(\mathbf{x}) - \mathbf{s}_\theta(\mathbf{x}, t) \|_2^2] \\ + \operatorname{KL}(p_T \mathrel\| \pi) \tag{13} \end{equation}
이 KL divergence에 대한 특별한 연결과 모델 학습을 위한 KL divergence를 최소화하는 것과 likelihood를 최대화하는 것이 동등하다는 점 때문에 우리는 λ(t)=g(t)2\lambda(t) = g(t)^2를 likelihood weighting function이라 부른다. 이 likelihood weighting 함수를 사용하여, score 기반 생성 모델을 학습하면 최신 auto-regressive 모델과 비교하거나 심지어 더 우수한 매우 높은 likelihood를 달성할 수 있다.

How to solve the reverse SDE

수치적 SDE solver를 사용하여 추정된 reverse SDE를 풀면 샘플 생성을 위한 reverse stochastic process를 시뮬레이션 할 수 있다. 가장 단순한 수치적 SDE solver는 Euler-Maruyama method 이다. 이 방법을 추정된 reverse SDE에 적용하면, 유한 time step과 작은 가우시안 노이즈를 사용하여 SDE를 이산화한다. 구체적으로 이것은 작은 음의 timestep Δt≈0\Delta t \approx 0을 선택하고 t←Tt \leftarrow T로 초기화한 다음 t≈0t \approx 0가 될 때까지 다음 절차를 반복한다.
Δx←[f(x,t)−g2(t)sθ(x,t)]Δt+g(t)∣Δt∣ztx←x+Δxt←t+Δt,\begin{aligned} \Delta \mathbf{x} &\gets [\mathbf{f}(\mathbf{x}, t) - g^2(t) \mathbf{s}_\theta(\mathbf{x}, t)]\Delta t + g(t) \sqrt{\vert \Delta t\vert }\mathbf{z}_t \\ \mathbf{x} &\gets \mathbf{x} + \Delta \mathbf{x}\\ t &\gets t + \Delta t, \end{aligned}
여기서 zt∼N(0,I)\mathbf{z}_t \sim \mathcal{N}(0, I)이다. Euler-Maruyama 방법은 랑주뱅 다이나믹스와 질적으로 유사하다. 둘 다 가우시안 노이즈를 사용하여 교란된 score 함수를 따라 x\bold{x}를 업데이트 한다.
Euler-Maruyama 방법 외에도 Milstein 방법, stochastic Runge-Kutta 방법 등 다른 수치 SDE Solver를 이용하여 샘플 생성을 위한 역 SDE를 풀 수 있다. [21]에서 Euler-Maruyama와 유사하지만 reverse-time SDEs를 풀기위해 더 맞춰진 reverse diffusion solvoer를 제공한다. 보다 최근에는 [37]의 저자들은 adaptive step-size SDE solver를 소개했는데, 이것은 더 나은 품질로 더 빠르게 샘플을 생성할 수 있다.
게다가 reverse SDE에는 훨씬 더 유연한 샘플링 방식을 허용하는 두 가지 특별한 속성이 있다.
•
time-dependent score 기반 모델 sθ(x,t)\mathbf{s}_\theta(\mathbf{x}, t)을 통해 ∇xlog⁡pt(x)\nabla_\mathbf{x} \log p_t(\mathbf{x})의 추정치를 갖는다.
•
우리는 각 marginal 분포 pt(x)p_t(\mathbf{x})의 샘플링에만 신경 쓰면 된다. 다양한 timestep에서 얻은 샘플은 임의의 상관관계를 가질 수 있으며 reverse SDE에서 샘플된 특정 궤적을 형성할 필요는 없다.
이 두 속성의 결과로 수치적 SDE solver에서 얻어진 궤적을 fine-tune 하기 위해 MCMC 접근을 적용할 수 있다. 구체적으로 우리는 Predictor-Corrector samplers를 제안한다. predictor는 기존의 샘플 x(t)∼pt(x)\mathbf{x}(t) \sim p_t(\mathbf{x})에서 x(t+Δt)∼pt+Δt(x)\mathbf{x}(t + \Delta t) \sim p_{t+\Delta t}(\mathbf{x})을 예측하는 임의의 수치적 SDE solver일 수 있다. corrector는 Langevin dynamics나 Hamiltoninan Monte Carlo 같은 score 함수에만 의존하는 임의의 MCMC 절차일 수 있다.
Predictor-Corrector sampler의 각 단계에서 우선 적절한 step size Δt<0\Delta t < 0을 고르기 위해 predictor를 사용하고 그 다음 현재 샘플 x(t)\mathbf{x}(t)을 이용해서 x(t+Δt)\mathbf{x}(t + \Delta t)를 예측한다. 그 다음 몇 개의 corrector step을 실행하여 score 기반 모델 sθ(x,t+Δt)\mathbf{s}_\theta(\mathbf{x}, t + \Delta t)을 따라 샘플 x(t+Δt)\mathbf{x}(t + \Delta t)을 개선하여 x(t+Δt)\mathbf{x}(t + \Delta t)가 pt+Δt(x)p_{t+\Delta t}(\mathbf{x})에서 더 높은 품질의 샘플이 되도록 한다.
Predictor-Corrector 방법과 score 기반 모델의 더 나은 아키텍쳐를 사용하여 CIFAR-10(FID와 Inception score로 측정된)에 대한 샘플 품질에서 최신 성능을 달성했다. 현시점까지 최고의 GAN 모델(StyleGAN2 + ADA)을 능가했다.
Method
FID ↓
Inception score ↑
StyleGAN2 + ADA [39]
2.92
9.83
Ours
2.20
9.89
또한 샘플링 방법은 매우 높은 차원 데이터에 대해서도 확장 가능하다. 예컨대 1024x1024 해상도의 높은 fidelity 이미지를 성공적으로 생성할 수 있다.

Probability flow ODE

높은 품질 샘플을 생성하는 능력에도 불구하고 Langevin MCMC와 SDE solver에 기반하는 샘플러는 score 기반 생성 모델의 정확한 log likelihood를 계산하는 방법을 제공하지 않는다. 아래에 ordinary differential equations(ODEs)에 기반한 샘플러를 소개한다. 이것은 정확한 likelihood 계산을 허용한다.
[21]에서 이것이 임의의 SDE를 marginal 분포 {pt(x)}t∈[0,T]\{ p_t(\mathbf{x}) \}_{t \in [0, T]}를 변경하지 않고 ODE로 변환하는 것이 가능함을 보인다. 따라서 이 ODE를 풀면 reverse SDE와 동일한 분포에서 샘플링할 수 있다. SDE에 해당하는 ODE를 probability flow ODE(PF ODE)라고 부르고 다음과 같이 주어진다.
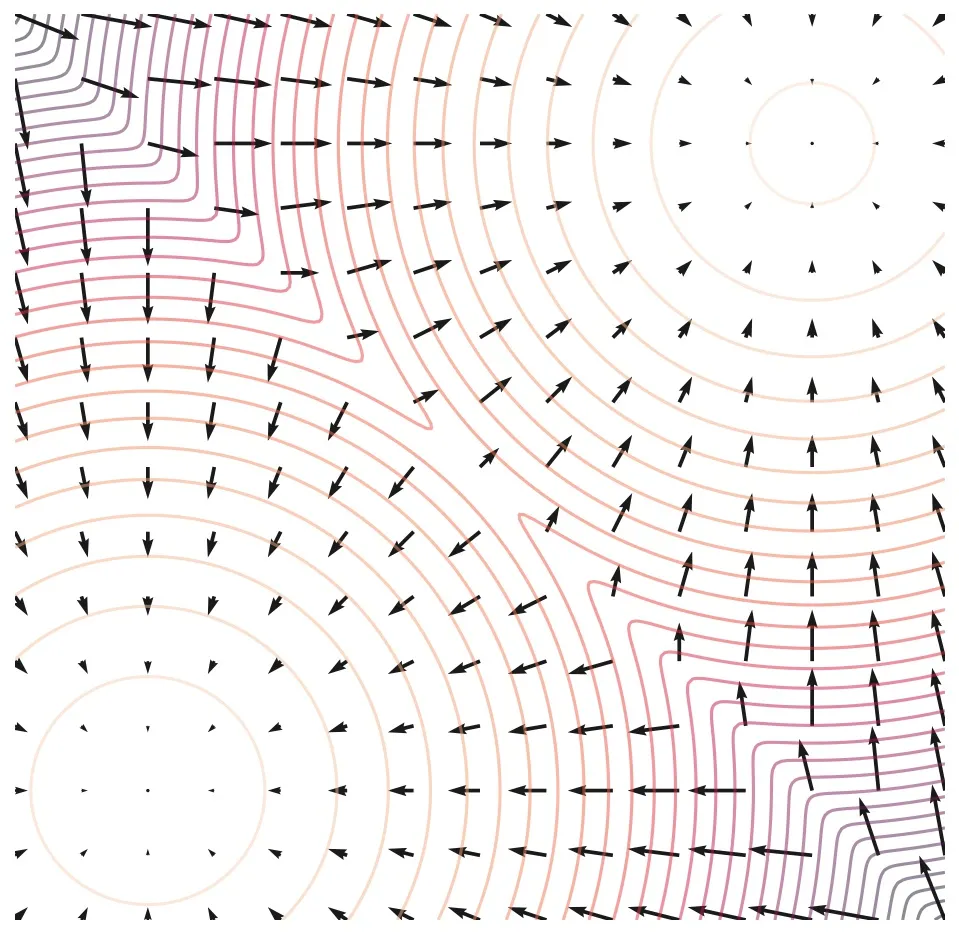
dx=[f(x,t)−12g2(t)∇xlog⁡pt(x)]dt\begin{equation} \mathrm{d} \mathbf{x} = \bigg[\mathbf{f}(\mathbf{x}, t) - \frac{1}{2}g^2(t) \nabla_\mathbf{x} \log p_t(\mathbf{x})\bigg] \mathrm{d}t \tag{14} \end{equation}
아래 그림은 SDE와 PF ODE 모두의 궤적을 보여준다. ODE 궤적이 SDE 궤적 보다 눈에 띄게 더 smooth 하다. 그들은 marginal 분포 {pt(x)}t∈[0,T]\{ p_t(\mathbf{x}) \}_{t \in [0, T]}의 동일한 집합을 공유하여, 동일한 데이터 분포를 동일한 prior 분포로 변환하고 그 반대의 경우도 마찬가지다. 즉 PF ODE를 풀어서 얻은 궤적은 SDE 궤적과 동일한 marginal 분포를 갖는다.
이 PF ODE 공식은 몇가지 고유한 장점을 갖는다.
∇xlog⁡pt(x)\nabla_\mathbf{x} \log p_t(\mathbf{x})가 자신의 근사치 sθ(x,t)\mathbf{s}_\theta(\mathbf{x}, t)로 대체될 때, PF ODE는 neural ODE의 특별한 경우가 된다. 특히 이것은 PF ODE가 데이터 분포 p0(x)p_0(\mathbf{x})를 prior 노이즈 분포 pT(x)p_T(\mathbf{x})로 변환하고(이것이 SDE와 동일한 marginal 분포를 공유하기 때문에) 완전히 가역이기 때문에 continuous normalizing flows의 예이다.
As such(이와 같이), PF ODE는 정확한 log-likelihood 계산을 포함하여 neural ODE 또는 continuous normalizing flows의 모든 속성을 내재한다. 특히 instantaneous change-of-variable 공식을 활용하여 수치적 ODE solver를 사용하여 알려진 prior 밀도 pTp_T에서 unknown 데이터 밀도 p0p_0을 계산할 수 있다.
실제로 우리의 모델은 maximum likelihood 학습 없이도 uniformly dequantized CIFAR-10 이미지에 대해 log-likelihood의 최신 성능을 달성했다.
Method
Negative log-likelihood (bits/dim) ↓
RealNVP
3.49
iResNet
3.45
Glow
3.35
FFJORD
3.40
Flow++
3.29
Ours
2.99
이전에 논의한 likelihood weighting을 사용하여 score 기반 모델을 학습하고 variational dequantization을 사용하여 이산 이미지에 대해 likelihood를 얻으면, (임의의 데이터 증강 없이) 최신 auto-regressive 모델과 비슷하거나 더 우수한 성능을 달성했다.
Method
Negative log-likelihood (bits/dim) ↓ on CIFAR-10
Negative log-likelihood (bits/dim) ↓ on ImageNet 32x32
Sparse Transformer
2.80
-
Image Transformer
2.90
3.77
Ours
2.83
3.76

Controllable generation for inverse problem solving

score 기반 생성 모델은 inverse 문제를 푸는데 특히 적합하다. 본질적으로 inverse 문제는 베이지안 추론 문제와 동일하다. x\bold{x}와 y\bold{y}를 두 확률 변수라하고 x\bold{x}에서 y\bold{y}를 생성하는 forward process인 전이 확률 분포 p(y∣x)p(\bold{y}|\bold{x})를 알고 있다고 가정하자. inverse 문제는 p(x∣y)p(\bold{x}|\bold{y})를 계산하는 것이다. 베이지안 규칙을 따라 p(x∣y)=p(x)p(y∣x)/∫p(x)p(y∣x)dxp(\mathbf{x} \mid \mathbf{y}) = p(\mathbf{x}) p(\mathbf{y} \mid \mathbf{x}) / \int p(\mathbf{x}) p(\mathbf{y} \mid \mathbf{x}) \mathrm{d} \mathbf{x}를 갖는다. 이 표현식은 양 변에 x\bold{x}에 관한 gradient를 취해서 매우 단순화시킬 수 있다. 이것은 score 함수에 대한 다음의 베이지안 규칙을 이끈다.
∇xlog⁡p(x∣y)=∇xlog⁡p(x)+∇xlog⁡p(y∣x)(15)\begin{equation} \nabla_\mathbf{x} \log p(\mathbf{x} \mid \mathbf{y}) = \nabla_\mathbf{x} \log p(\mathbf{x}) + \nabla_\mathbf{x} \log p(\mathbf{y} \mid \mathbf{x}) \end{equation} \tag{15}
score matching을 통해 unconditional 데이터 분포의 score 함수를 추정하도록 모델을 핛브할 수 있다. 즉 sθ(x)≈∇xlog⁡p(x)\mathbf{s}_\theta(\mathbf{x}) \approx \nabla_\mathbf{x} \log p(\mathbf{x}). 이것은 알려진 forward process p(y∣x)p(\bold{y}|\bold{x})에서 방정식 (15)을 통해 posterior score 함수 ∇xlog⁡p(x∣y)\nabla_\mathbf{x} \log p(\mathbf{x} \mid \mathbf{y})를 쉽게 계산할 수 있게 한다.
UT Austin의 최근 연구는 score 기반 생성 모델이 MRI 가속화와 같은 의료 이미지에서 inverse 문제를 해결하는데 적용할 수 있음을 보였다. 동시에 우리는 가속 MRI 뿐만 아니라 희소 뷰 CT에서도 score 기반 생성 모델의 우수한 성능을 입증했다. 우리는 supervised 또는 unrolled deep learning 접근과 비슷하거나 더 나은 성능을 달성할 수 있었으며 테스트 시간에 다양한 측정 과정에 대해 더 견고했다.
아래에서 컴퓨터 비전에 대한 inverse 문제를 해결하는 몇 가지 예제를 보인다.

Connection to diffusion models and others

나는 고차원 데이터셋에 대한 deep energy-based 모델을 학습시키기 위해 score matching을 확장하려고 노력하던 2019년부터 score 기반 생성 모델링에 대한 작업을 시작했다. 이를 위한 첫 번째 시도로 sliced score matching로 이어졌다. 에너지 기반 모델 훈련을 위한 sliced score matching의 확장성에도 불구하고, 놀랍게도 이런 모델에서 Langevin 샘플링을 하면 MNIST 데이터셋에서 조차 합리적인 샘플을 생성하는데 실패한다는 사실을 발견했다. 나는 이 이슈를 조사하기 시작했고 극도로 좋은 샘플을 만들 수 있는 3가지 핵심 개선을 발견했다. (1) mutliple scale 노이즈를 사용하여 데이터를 교란하고, 각 노이즈 스케일에 대해 score 기반 모델을 학습. (2) score 기반 모델을 위해 U-Net 아키텍쳐(우리는 U-Net의 현대 버전인 RefineNet을 사용했다)를 사용. (3) 각 노이즈 스케일에 Lagevin MCMC를 적용하고 그것들을 서로 chaining 함. 이런 방법들을 사용하여 CIFAR-10에서 최신 Inception score를 얻을 수 있었고(최고 수준의 GAN 보다 좋았다) 해상도 256x256의 높은 품질의 이미지를 생성할 수 있었다.
노이즈의 multiple 스케일을 사용하여 데이터를 교란하는 아이디어는 score 기반 생성 모델에 고유한 것이 아니다. 예컨대 simulated annealing, annealed importance sampling, diffusion probabilistic model, infusion training, generative stochastic network에 대한 variational walkback이 있다. 이런 작업들 중에 diffusion probabilistic modeling은 아마 score 기반 생성 모델링과 가장 가까울 것이다. diffusion probabilistic 모델은 hierarchical latent variable 모델로 2015년에 Jascha와 그의 대학에서 처음 제안되었다. 이것은 variational decoder를 학습하여 데이터를 노이즈로 교란하는 이산 diffusion 프로세스를 reverse 하여 샘플을 생성한다. 이 작업에 대한 인식이 없었기 때문에 score 기반 생성 모델링은 매우 다양한 관점에서 독립적으로 동기 부여 받았다. 둘 다 노이즈의 multiple 스케일을 사용하여 데이터를 교란하지만, score 기반 모델은 score matching으로 학습되고 랑주뱅 역학으로 샘플링 되는 반면 diffusion probabilistic 모델은 evidence lower bound(ELBO)로 학습되고 학습된 decoder로 샘플링 되기 때문에 당시에 score 기반 모델과 diffusion probabilistic 모델 간의 연결은 표면적인 것으로 보였다.
2020년에 Jonathan Ho와 그의 대학은 diffusion probabilistic 모델의 경험적 성능을 크게 개선했고 처음으로 score 기반 생성 모델링과 깊은 연결을 unveiled(공개했다) 그들은 diffusion probabilistic 모델을 학습하기 위해 사용된 ELBO가 score 기반 생성 모델링에 사용된 score matching 목적의 weighted combination과 근본적으로 동등함을 보였다. 게다가 디코더를 U-Net 아키텍처의 score 기반 모델 시퀀스로 파라미터화하여, 그들은 diffusion probabilistic 모델 또한 GAN과 비슷하거나 능가하는 높은 품질의 이미지 샘플을 생성할 수 있음을 처음으로 보였다.
그들의 작업에 영감을 받아 우리는 ICLR 2021 논문에서 diffusion 모델과 score 기반 생성 모델 사이의 관계를 더 조사했다. 우리는 diffusion probabilistic 모델의 샘플링 방법이 score 기반 모델의 annealed Langevin dynamics과 통합되어 더 강력한 샘플러(Predictor-Corrector sampler)를 생성할 수 있음을 발견했다. 노이즈 스케일의 수를 무한으로 일반화하여 우리는 score 기반 생성 모델과 diffusion probabilistic 모델이 모두 score 함수에 의해 결정되는 stochastic differential equation의 이산화로 볼 수 있음을 더 증명했다. 이 작업을 통해 score 기반 생성 모델과 diffusion probabilistic 모델을 통합된 프레임워크로 연결되었다.
종합적으로, 이 최신 발전 동향은 multiple 노이즈 교란을 사용하는 score 기반 생성 모델링과 diffusion probabilistic 모델이 모두 동일한 모델 계열의 다양한 관점이라는 것을 시사하는 것 같다. 이는 역사적으로 파동 역학과 행렬 역학이 물리학의 역사에서 양자 역학의 동일한 공식인 것과 매우 유사하다. score matching과 score 기반 모델의 관점에서는 log-likelihood의 정확한 계산하고 자연스럽게 inverse 문제를 풀어서 에너지 기반 모델, Schrödinger bridge와 optimal transport와 직접 연결될 수 있다. diffusion 모델의 관점은 VAE, 무손실 압축과 자연스럽게 연결되며 variational probabilistic inference와 직접 통합될 수 있다. 이 블로그 포스트는 첫 번째 관점에 초점을 맞추고 있지만 관심 있는 독자들에게 diffusion 모델의 대안 관점에 관해 대해서도 배우기를 적극 권장한다. (Lilian Weng의 훌륭한 블로그 참조. What are Diffusion Models? | Lil'Log (lilianweng.github.io))
최근 score 기반 생성 모델이나 diffusion probabilistic 모델에 대한 많은 연구가 양쪽의 연구의 지식에 깊게 영향 받았다(Oxford 대학의 연구자이 큐레이팅한 웹사이트 참조). score 기반 생성 모델과 diffusion 모델 사이의 깊은 연결에도 불구하고, 둘 다 속하는 모델 계열을 포괄하는 용어를 만들기는 어렵다. DeepMind의 몇몇 연구진은 ‘Generative Diffusion Processes’라고 부르자고 제안했다. 이것이 향후 커뮤니티에서 채택될 지는 지켜봐야 할 것 같다.

Concluding remarks

(생략)
Made with