Search
Duplicate

AI/ Paper/ Denoising Diffusion Probabilistic Models

Denoising Diffusion Probabilistic Models
We present high quality image synthesis results using diffusion probabilistic models, a class of latent variable models inspired by considerations from nonequilibrium thermodynamics. Our best...
https://arxiv.org/abs/2006.11239

Abstract

우리는 diffusion probabilistic model을 사용한 고품질 이미지 합성 결과를 제시한다. 이것은 non-equilibrium thermodynamics(비평형 열역학)에서 영감 받은 latent 변수 모델의 한 종류이다. 우리의 최고 결과는 diffusion probabilistic 모델과 Langevin dynamics를 사용하는 denoising score matching 사이의 새로운 연결을 기반으로 설계된 weighted variational bound를 학습하여 얻어지며, 이 모델은 autoregressive decoding의 일반화로 해석할 수 있는 점진적 손실 압축 방식을 자연스럽게 허용한다. unconditional CIFAR10 데이터셋에서 9.46의 Inception score와 3.17의 최첨단 FID score를 얻는다. 256x256 LSUN에서는 ProgressiveGan과 유사한 샘플링 품질을 달성한다. 우리의 구현은 git에서 사용 가능하다.
diffusion
hojonathanho

1 Introduction

최근 다양한 데이터 모달리티에서 고품질 샘플을 생성하는 심층 생성 모델이 주목 받고 있다. Generative Adversarial Network(GAN), Autoregressive Models, Flows, Variational Autoencoder(VAE)는 주목할만한 이미지와 오디오 샘플을 합성했고, energy-based modeling과 score-matching에서도 놀라울만한 진보가 이루어져 GAN과 비교할만한 이미지를 생성한다.
이 논문에서는 diffusion probabilistic model의 발전을 제시한다. diffusion probabilistic model(단순함을 위해 diffusion model이라 부름)은 유한 시간 후에 데이터와 일치하는 샘플을 생성하기 위해 variational inference를 사용하여 파라미터화된 Markov chain이다. 이 Markov chain의 체인의 전이는 샘플링의 반대 방향에서 데이터에 점진적으로 noise를 추가해 신호를 파괴하는 diffusion process를 reverse하도록 학습된다. diffusion이 소량의 가우시안 노이즈로 구성되면, 샘플링 체인의 전이도 조건부 가우시안으로 설정할 수 있어 간단한 neural network 파라미터화를 가능하게 한다.
Diffusion model은 정의가 간단하고 학습이 효과적이지만 우리가 아는 한 고품질 샘플을 생성하는 능력을 시연한 적이 없었다. 우리는 diffusion model이 실제로 고품질 샘플을 생성하는 능력을 보이며, 때때로 다른 유형의 생성 모델의 공개된 결과보다 더 낫다(섹션 4). 또한 diffusion model의 특정한 파라미터화가 학습하는 동안 여러 노이즈 레벨에 대한 denoising score matching과 샘플링하는 동안 annealed Langevin dynamics를 사용하는 것과 동등함을 보인다(섹션 3.2). 우리는 이러한 파라미터화를 사용하여 최고의 샘플 품질을 달성했으며(섹션 4.2), 이 동등성이 우리의 주요 기여 중 하나라고 간주한다.
비록 샘플 품질이 뛰어나지만, 우리의 모델은 다른 likelihood 기반 모델에 비교하여 경쟁적인 log-likelihood를 갖지 못한다(그러나 우리의 모델은 energy-based model과 score matching에서 리포트된 annealed importance sampling의 큰 추정치보다 더 나은 log-likelihood를 갖는다). 우리는 모델의 무손실 코드 길이의 대부분이 감지할 수 없는 이미지 디테일을 설명하도록 소비된다는 것을 발견했다(섹션 4.3). 우리는 이 현상을 손실 압축의 관점에서 더 정교하게 분석하고 diffusion model의 샘플링 절차가 progressive decoding의 한 유형이며, 이는 autoregressive 모델에서 가능한 것보다 훨씬 일반화된 bit ordering에 따른 autoregressive decoding과 유사하다는 것을 보인다.

2 Background

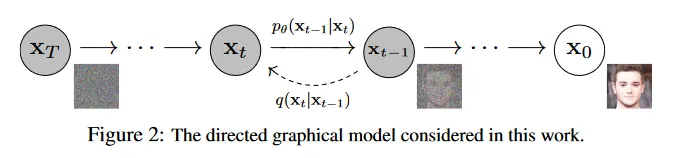
diffusion model은 pθ(x0):=∫pθ(x0:T)dx1:Tp_\theta(\bold{x}_0) := \int p_\theta(\bold{x}_{0:T})d\bold{x}_{1:T} 형식의 latent 변수 모델이다. 여기서 x1,...,xT\bold{x}_1, ...,\bold{x}_T는 데이터 x0∼q(x0)\bold{x}_0 \sim q(\bold{x}_0)과 동일한 차원의 latent이다. 결합 분포 pθ(x0:T)p_\theta(\bold{x}_{0:T})는 reverse process라 부르고 p(xT)=N(xT;0,I)p(\bold{x}_T) = \mathcal{N}(\bold{x}_T;\bold{0},\bold{I})에서 시작하는 학습된 가우시안 전이를 갖는 Markov Chain으로 정의된다.
pθ(x0:T):=p(xT)∏t=1Tpθ(xt−1∣xt),pθ(xt−1∣xt):=N(xt−1;μθ(xt,t),Σθ(xt,t))(1)\begin{aligned} p_\theta(\bold{x}_{0:T}) &:= p(\bold{x}_T)\prod_{t=1}^Tp_\theta(\bold{x}_{t-1}|\bold{x}_t), \\p_\theta(\bold{x}_{t-1}|\bold{x}_t) &:= \mathcal{N}(\bold{x}_{t-1};\boldsymbol{\mu}_\theta(\bold{x}_t,t),\boldsymbol{\Sigma}_\theta(\bold{x}_t, t)) \end{aligned} \tag{1}
diffusion 모델을 다른 유형의 latent 변수 모델과 구별하는 것은 근사 posterior q(x1:T∣x0)q(\bold{x}_{1:T}|\bold{x}_0)이다. 이것은 forward process 또는 diffusion process라 부르는 고정된 Markov chain으로 분산 스케쥴 β1,...,βT\beta_1,...,\beta_T을 따라 데이터에 가우시안 노이즈를 점진적으로 추가한다.
q(x1:T∣x0):=∏t=1Tq(xt∣xt−1)q(xt∣xt−1):=N(xt;1−βtxt−1,βtI)(2)\begin{aligned} q(\bold{x}_{1:T}|\bold{x}_0) &:= \prod_{t=1}^T q(\bold{x}_t|\bold{x}_{t-1}) \\ q(\bold{x}_t|\bold{x}_{t-1}) &:= \mathcal{N}(\bold{x}_t;\sqrt{1-\beta_t}\bold{x}_{t-1}, \beta_t\bold{I})\end{aligned} \tag{2}
학습은 negative log likelihood에 대한 일반적인 variational bound를 최적화하여 수행된다.
E[−log⁡pθ(x0)]≤Eq[−log⁡pθ(x0:T)q(x1:T∣xt)]=Eq[−log⁡p(xT)−∑t≥1log⁡pθ(xt−1∣xt)q(xt∣xt−1)]:=L(3)\mathbb{E}[-\log p_\theta(\bold{x}_0)] \le \mathbb{E}_q \left[-\log{p_\theta(\bold{x}_{0:T}) \over q(\bold{x}_{1:T}|\bold{x}_t)} \right] = \mathbb{E}_q\left[-\log p(\bold{x}_T) - \sum_{t\ge1}\log{p_\theta(\bold{x}_{t-1}|\bold{x}_t) \over q(\bold{x}_t|\bold{x}_{t-1})} \right] := L\tag{3}
forward process 분산 βt\beta_t는 reparameterization으로 학습되거나 또는 하이퍼파라미터로 고정될 수 있다. reverse process의 표현력을 보장하는 한 요소는 pθ(xt−1∣xt)p_\theta(\bold{x}_{t-1}|\bold{x}_t)의 가우시안 조건부를 선택하는 것이다. 이는 βt\beta_t가 작을 때 두 프로세스 모두 동일한 함수 형식을 갖기 때문이다.
forward process의 주목할만한 속성은 임의의 timestep tt에서 xt\bold{x}_t를 닫힌 형식으로 샘플링할 수 있다는 것이다. αt:=1−βt\alpha_t := 1-\beta_t와 αˉt:=∏s=1tαs\bar{\alpha}_t := \prod_{s=1}^t \alpha_s를 정의하여 다음처럼 계산된다.
q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)(4)q(\bold{x}_t|\bold{x}_0) = \mathcal{N}(\bold{x}_t;\sqrt{\bar{\alpha}_t}\bold{x}_0, (1-\bar{\alpha}_t)\bold{I}) \tag{4}
그러므로 효율적인 학습은 stochastic gradient descent를 사용하여 LL의 임의의 항을 최적함으로써 가능해진다. 추가적인 개선은 LL를 다음과 같이 재작성하여 분산을 축소하는 것에서 온다.
Eq[DKL(q(xT∣x0)∥p(xT))⏟LT+∑t>1DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))⏟Lt−1−log⁡pθ(x0∣x1)⏟L0](5)\mathbb{E}_q \left[\underbrace{D_\text{KL}(q(\bold{x}_T|\bold{x}_0) \| p(\bold{x}_T))}_{L_T} + \sum_{t> 1} \underbrace{D_\text{KL}(q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0) \| p_\theta(\bold{x}_{t-1}|\bold{x}_t))}_{L_{t-1}} \underbrace{-\log p_\theta(\bold{x}_0|\bold{x}_1)}_{L_0} \right] \tag{5}
(자세한 내용은 부록 A 참조. 항목의 라벨은 섹션 3에서 사용된다.) 방정식 5는 KL divergence를 사용하여 pθ(xt−1∣xt)p_\theta(\bold{x}_{t-1}|\bold{x}_t)를 forward process posterior와 직접 비교한다. 이것은 x0\bold{x}_0에 조건부일 때 다루기 용이하다.
q(xt−1∣xt,x0)=N(xt−1;μ~t(xt,x0),β~tI)where μ~t(xt,x0):=αˉt−1βt1−αˉtx0+αt(1−αˉt−1)1−αˉtxt and β~t:=1−αˉt−11−αˉtβt\begin{align} q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0) &= \mathcal{N}(\bold{x}_{t-1};\tilde{\boldsymbol{\mu}}_t(\bold{x}_t, \bold{x}_0), \tilde{\beta}_t\bold{I}) \tag{6} \\ \text{where } \tilde{\boldsymbol{\mu}}_t(\bold{x}_t,\bold{x}_0) &:= {\sqrt{\bar{\alpha}_{t-1}}\beta_t \over 1-\bar{\alpha}_t}\bold{x}_0 + {\sqrt{\alpha}_t(1-\bar{\alpha}_{t-1}) \over 1 - \bar{\alpha}_t}\bold{x}_t \text{ and } \tilde{\beta}_t := {1-\bar{\alpha}_{t-1} \over 1-\bar{\alpha}_t} \beta_t \tag{7} \end{align}
결과적으로 방정식 5에서 모든 KL divergence는 가우시안 사이의 비교이므로, 높은 분산의 Monte Carlo 추정 대신 Rao-Blackwellized 방식으로 닫힌 형식으로 계산될 수 있다.

3 Diffusion models and denoising autoencoders

Diffusion model은 제한된 클래스의 latent 변수 모델로 보일 수 있지만 구현에서 많은 자유도를 허용한다. 사용자는 forward process의 분산 βt\beta_t, 모델 아키텍쳐, reverse process의 가우시안 분포 파라미터를 선택해야 한다. 우리의 선택을 안내하기 위해 우리는 diffusion model과 denoising score matching(섹션 3.2) 사이의 새로운 명시적 연결을 설정하여, diffusion model을 위한 간단한 weighted variational bound objective을 이끈다. 궁극적으로 우리의 모델 설계는 단순성과 실험 결과에 의해 정당화된다(섹션 4). 우리의 논의는 방정식 5의 항목을 기준으로 분류된다.

3.1 Forward process and LTL_T

우리는 forward process 분산 βt\beta_t를 상수로 고정하는 대신 reparameterization에 의해 학습가능하다(섹션 4)는 사실을 무시한다. 따라서 우리의 구현에서 근사치 posterior qq는 학습 가능한 파라미터를 갖지 않는다. 따라서 LTL_T는 학습하는 동안 상수이고 무시할 수 있다.

3.2 Reverse process and L1:T−1L_{1:T-1}

이제 1<t≤T1 < t \le T에 대해 pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))p_\theta(\bold{x}_{t-1}|\bold{x}_t) = \mathcal{N}(\bold{x}_{t-1};\boldsymbol{\mu}_\theta(\bold{x}_t,t), \boldsymbol{\Sigma}_\theta(\bold{x}_t, t))에서 우리의 선택을 논의한다. 우선 Σθ(xt,t)=σt2I\boldsymbol{\Sigma}_\theta(\bold{x}_t,t) = \sigma_t^2\bold{I}를 학습되지 않는 시간 종속 상수로 설정한다. 실험적으로 σt2=βt\sigma_t^2 = \beta_t와 σt2=β~t=1−αˉt−11−αˉtβt\sigma_t^2 = \tilde{\beta}_t = {1-\bar{\alpha}_{t-1} \over 1- \bar{\alpha}_t}\beta_t가 유사한 결과를 보였다. 첫 번째 선택은 x0∼N(0,I)\bold{x}_0 \sim \mathcal{N}(\bold{0}, \bold{I})일 때 최적이고, 두 번째 선택은 x0\bold{x}_0가 한 점에서 결정론적으로 설정될 때 최적이다. 이 두 가지는 데이터가 좌표별 단위 분산을 가질 때, reverse process entropy에 대한 upper와 lower bound에 해당하는 극단적인 선택이다.
둘째, 평균 μθ(xt,t)\boldsymbol{\mu}_\theta(\bold{x}_t,t)를 나타내기 위해 우리는 LtL_t에 대한 다음 분석에서 동기부여 받은 특정 파라미터를 제안한다. pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),σt2I)p_\theta(\bold{x}_{t-1}|\bold{x}_t) = \mathcal{N}(\bold{x}_{t-1};\boldsymbol{\mu}_\theta(\bold{x}_t, t), \sigma_t^2\bold{I})일 때, 다음처럼 작성할 수 있다.
Lt−1=Eq[12σt2∥μ~t(xt,x0)−μθ(xt,t)∥2]+C(8)L_{t-1} = \mathbb{E}_q \left[ {1\over 2\sigma_t^2} \| \tilde{\boldsymbol{\mu}}_t(\bold{x}_t, \bold{x}_0) - \boldsymbol{\mu}_\theta(\bold{x}_t,t) \|^2 \right] + C \tag{8}
여기서 CC는 θ\theta에 의존하지 않는 상수이다. 따라서 μθ\boldsymbol{\mu}_\theta의 가장 간단한 파라미터화는 forward process posterior mean인 μ~t\tilde{\boldsymbol{\mu}}_t를 예측하는 모델임을 볼 수 있다.
그러나 우리는 방정식 8을 추가로 확장할 수 있고 방정식 4를 xt(x0,ϵ)=αˉtx0+1−αˉtϵ\bold{x}_t(\bold{x}_0,\epsilon) = \sqrt{\bar{\alpha}_t}\bold{x}_0 + \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon} (여기서 ϵ∼N(0,I)\boldsymbol{\epsilon} \sim \mathcal{N}(\bold{0}, \bold{I}))으로 reparameterizing하고 forward process posterior 공식(7)을 적용할 수 있다.
Lt−1−C=Ex0,ϵ[12σt2∥μ~t(xt(x0,ϵ),1αˉt(xt(x0,ϵ)−1−αˉtϵ)−μθ(xt(x0,ϵ),t))∥2]=Ex0,ϵ[12σt2∥1αt(xt(x0,ϵ)−βt1−αˉtϵ)−μθ(xt(x0,ϵ),t)∥2]\begin{align} L_{t-1} - C &= \mathbb{E}_{\bold{x}_0, \boldsymbol{\epsilon}} \left[{1\over2\sigma_t^2} \left\|\tilde{\boldsymbol{\mu}}_t \left(\bold{x}_t(\bold{x}_0, \boldsymbol{\epsilon}), {1 \over \sqrt{\bar{\alpha}_t}}(\bold{x}_t(\bold{x}_0,\boldsymbol{\epsilon}) - \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon}) - \boldsymbol{\mu}_\theta(\bold{x}_t(\bold{x}_0,\boldsymbol{\epsilon}),t) \right) \right\|^2 \right] \tag{9} \\ &= \mathbb{E}_{\bold{x}_0, \boldsymbol{\epsilon}} \left[{1\over 2\sigma_t^2} \left\|{1\over \sqrt{\alpha}_t} \left(\bold{x}_t(\bold{x}_0, \boldsymbol{\epsilon}) - {\beta_t \over \sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon} \right) - \boldsymbol{\mu}_\theta(\bold{x}_t(\bold{x}_0,\boldsymbol{\epsilon}),t) \right\|^2 \right] \tag{10} \end{align}
방정식 10은 μθ\boldsymbol{\mu}_\theta가 xt\bold{x}_t가 주어질 때, 1αt(xt−βt1−αˉtϵ){1\over\sqrt{\alpha_t}}\left(\bold{x}_t - {\beta_t \over \sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon} \right)를 예측해야 함을 드러낸다. xt\bold{x}_t는 모델의 입력으로 가능하므로 우리는 다음과 같은 파라미터화를 선택할 수 있다.
μθ(xt,t)=μ~t(xt,1αˉt(xt−1−αˉtϵθ(xt)))=1αt(xt−βt1−αˉtϵθ(xt,t))(11)\boldsymbol{\mu}_\theta(\bold{x}_t, t) = \tilde{\boldsymbol{\mu}}_t\left(\bold{x}_t, {1\over\sqrt{\bar{\alpha}}_t}(\bold{x}_t - \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon}_\theta(\bold{x}_t)) \right) = {1\over\sqrt{\alpha_t}} \left(\bold{x}_t - {\beta_t \over \sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon}_\theta(\bold{x}_t,t) \right) \tag{11}
여기서 ϵθ\boldsymbol{\epsilon}_\theta는 xt\bold{x}_t에서 ϵ\boldsymbol{\epsilon}를 예측하도록 설계된 함수 근사기이다. xt−1∼pθ(xt−1∣xt)\bold{x}_{t-1} \sim p_\theta(\bold{x}_{t-1}|\bold{x}_t)를 샘플하는 것은 xt−1=1αt(xt−βt1−αˉtϵθ(xt,t))+σtz\bold{x}_{t-1} = {1\over \sqrt{\alpha_t}} \left(\bold{x}_t - {\beta_t \over \sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\bold{x}_t, t) \right) + \sigma_t \bold{z}를 계산하는 것이다. 여기서 z∼N(0,I)\bold{z} \sim \mathcal{N}(\bold{0}, \bold{I}). 전체 샘플링 절차인 Algorithm 2는 ϵθ\boldsymbol{\epsilon}_\theta가 데이터 밀도의 학습된 gradient로 작동하는 Langevin dynamics와 유사하다. 또한 방정식 11을 파라미터화를 사용하면 방정식 10은 다음처럼 단순화 된다.
Ex0,ϵ[βt22σt2αt(1−αˉt)∥ϵ−ϵθ(αˉtx0+1−αˉtϵ,t∥2](12)\mathbb{E}_{\bold{x}_0,\boldsymbol{\epsilon}} \left[{\beta_t^2 \over 2\sigma_t^2 \alpha_t(1-\bar{\alpha}_t)} \| \boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\bold{x}_0 + \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon},t \|^2 \right] \tag{12}
이것은 multiple noise scale tt에 대한 denoising score matching과 유사하다. 방정식 12은 Langevin-like reverse process(11)에 대한 variational bound의 일부와 같으므로, denoising score matching과 유사한 목적을 최적화하는 것이 Langevin Dynamics과 유사한 샘플링 체인의 유한 시간 marginal 분포를 variational inference를 통해 맞추는 것과 동등하다는 것을 알 수 있다.
요약하면 우리는 reverse process mean 함수 근사기 μθ\boldsymbol{\mu}_\theta를 μ~t\tilde{\boldsymbol{\mu}}_t를 예측하도록 학습하거나 파라미터화를 수정하여 우리는 ϵ\boldsymbol{\epsilon}을 예측하도록 학습할 수 있다(또한 x0\bold{x}_0를 예측하는 방법도 가능하지만 실험 초기에 나쁜 샘플 품질을 이끄는 것을 발견했다.). 우리는 ϵ\boldsymbol{\epsilon}-예측 파라미터화가 Langevin dynamics와 유사하며, duffusion model의 variational bound를 denoising score matching과 유사한 목적으로 단순화 함을 보여주었다.
그럼에도 불구하고 이는 pθ(xt−1∣xt)p_\theta(\bold{x}_{t-1}|\bold{x}_t)의 또 다른 파라미터화이므로, 우리는 섹션 4에서 ϵ\boldsymbol{\epsilon} 예측과 μ~t\tilde{\boldsymbol{\mu}}_t 예측을 비교하는 ablation을 통해 그 효과를 검증한다.
Algorithm 2 Sampling
1.
xT∼N(0,I)\bold{x}_T \sim \mathcal{N}(\bold{0}, \bold{I})
2.
for t=T,...,1t = T, ..., 1 do
a.
z∼N(0,I)\bold{z} \sim \mathcal{N}(\bold{0}, \bold{I}) if t>1t > 1, else z=0\bold{z} = \bold{0}
b.
zt−1=1αt(xt−1−αt1−αˉtϵθ(xt,t))+σtz\bold{z}_{t-1} = {1\over\sqrt{\alpha_t}} \left(\bold{x}_t - {1-\alpha_t \over \sqrt{1-\bar{\alpha}_t}}\boldsymbol{\epsilon}_\theta(\bold{x}_t, t) \right) + \sigma_t\bold{z}
3.
end for
4.
return x0\bold{x}_0

3.3 Data scaling, reverse process decoder, and L0L_0

우리는 이미지 데이터가 {0,1,..,.255}\{0, 1, ..,. 255\}의 정수로 구성되고 [−1,1][-1, 1]로 선형적으로 스케일링한다고 가정한다. 이것은 신경망 reverse process가 표준 normal prior p(xT)p(\bold{x}_T)에서 시작하여 일관된 스케일의 입력을 처리하도록 보장한다. 이산 log likelihood를 얻기 위해, 우리는 reverse process의 마지막 항을 가우시안 N(x0;μθ(x1,1),σ12I)\mathcal{N}(\bold{x}_0; \boldsymbol{\mu}_\theta(\bold{x}_1, 1), \sigma_1^2\bold{I})에서 유도된 독립적인 이산 decoder로 설정한다.
pθ(x0∣x1)=∏i=1D∫δ−(x0i)δ+(x0i)N(x;μθi(xi,1),σ12)dxδ+(x)={∞x=1x+1255x<1δ−(x)={−∞x=−1x−1255x>−1(13)\begin{aligned} p_\theta(\bold{x}_0|\bold{x}_1) &= \prod_{i=1}^D \int_{\delta_-(x_0^i)}^{\delta_+(x_0^i)} \mathcal{N}(x;\mu_\theta^i(\bold{x}_i,1),\sigma_1^2) dx \\ \delta_+(x) &= \begin{cases} \infty & x = 1 \\ x + {1\over255} & x < 1 \end{cases} \\ \delta_-(x) &= \begin{cases} -\infty & x = -1 \\ x - {1\over255} & x > -1 \end{cases} \end{aligned} \tag{13}
여기서 DD는 데이터 차원이고 ii는 하나의 좌표를 추출하는 것을 나타낸다. (대신 조건부 autoregressiv model 같은 더 강력한 decoder를 통합하는 것도 가능하지만 우리는 미래 작업으로 남긴다). VAE decoder와 autoregressive model에서 사용된 이산화된 연속 분포와 유사하게, 여기서 우리의 선택은 variational bound가 이산 데이터의 무손실 코드 길이를 보장하며, 데이터에 노이즈를 추가하거나 scaling 연산의 Jacobian을 log likelihood에 통합할 필요가 없게 한다. 샘플링의 마지막에 우리는 μθ(x1,1)\boldsymbol{\mu}_\theta(\bold{x}_1, 1)을 노이즈 없음으로 표시한다.

3.4 Simplified training objective

위에 정의된 reverse process와 decoder를 사용하면, variational bound는 방정식 12와 13에서 유도된 항들로 구성되며, θ\theta에 대해 명확히 미분가능하고 학습에 바로 사용할 수 있다. 그러나 우리는 다음과 같은 variational bound의 변종을 따라 학습하는 것이 샘플 품질(과 더 단순한 구현)에 유익함을 발견한다.
Lsimple(θ):=Et,x0,ϵ[∥ϵ−ϵθ(αˉtx0+1−αˉtϵ,t)∥2](14)L_\text{simple}(\theta) := \mathbb{E}_{t, \bold{x}_0, \boldsymbol{\epsilon}}\left[\|\boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\bold{x}_0 + \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon},t)\|^2 \right] \tag{14}
여기서 tt는 11과 TT 사이에서 균등이다. t=1t=1은 이산 decoder 정의(13)의 적분이 가우시안 확률 밀도 함수와 bin width로 근사된 L0L_0에 해당하며, σ12\sigma_1^2과 엣지 효과를 무시한다. t>1t>1인 경우는 방정식 12의 unweighted 버전에 해당하며, 이는 NCSN denoising score matching model에서 사용된 loss 가중치와 유사하다(LTL_T는 forward process의 분산 βt\beta_t가 고정되어 있기 때문에 나타나지 않는다). Algorithm 1은 이러한 단순화된 목적을 사용하는 전체 학습 절차를 보인다.
우리의 단순화된 목적(14)는 방정식 12의 가중치를 폐기하기 때문에 표준 variational bound와 비교할 때 reconstruction의 서로 다른 측면을 강조하는 weighted variational bound이다. 특히 섹션 4에서 설정한 우리의 diffusion process는 작은 tt에 해당하는 loss 항을 down-weight한다. 이러한 항은 네트워크가 매우 작은 양의 노이즈를 가진 데이터를 denoise 하도록 학습하기 때문에, 이것들을 down-weight하면 네트워크가 더 큰 tt 항에서 더 어려운 denoising task에 집중할 수 있게 된다. 우리의 실험에서 이 reweighting이 더 나은 품질을 이끈다는 것을 보인다.
Algorithm 1 Training
1.
repeat
a.
x0∼q(x0)\bold{x}_0 \sim q(\bold{x}_0)
b.
t∼Uniform({1,...,T})t \sim \text{Uniform}(\{1,...,T\})
c.
ϵ∼N(0,I)\boldsymbol{\epsilon} \sim \mathcal{N}(\bold{0}, \bold{I})
d.
Task gradient descent step on ∇θ∥ϵ−ϵθ(αˉtx0+1−αˉtϵ,t)∥2\nabla_\theta \|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\bold{x}_0 + \sqrt{1-\bar{\alpha}_t}\boldsymbol{\epsilon}, t)\|^2
2.
until converged

4 Experiments

우리는 모든 실험에서 T=1000T=1000을 설정하여 샘플링 중 신경망 평가 횟수가 이전 연구 [53, 55]와 일치하도록 했다. forward process 분산은 β1=10−4\beta_1 = 10^{-4}에서 βT=0.02\beta_T = 0.02로 선형으로 증가하는 상수를 사용한다. 이러한 상수는 데이터를 [−1,1][-1, 1]로 스케일링한 상태에서 상대적으로 작게 선택되었으며, reverse와 forward process가 대략 동일한 함수 형식을 같도록 보장하면서 xT\bold{x}_T에서 신호대잡음비가 가능한 작게 유지되도록 했다(우리 실험에서 차원 당 LT=DKL(q(xT∣x0)∥N(0,I))≈10−5L_T = D_{KL}(q(\bold{x}_T|\bold{x}_0) \|\mathcal{N}(\bold{0}, \bold{I})) \approx 10^{-5} bit).
reverse process를 표현하기 위해 우리는 unmasked PixelCNN++와 유사한 U-Net backbone을 사용하고 group normalization을 전반적으로 적용했다. 파라미터는 시간에 걸쳐 공유되고, 네트워크에 Transformer sinusoidal position embedding을 사용해 지정한다. 우리는 16x16 feature map 해상도에서 self-attention을 사용한다. 자세한 내용은 부록 B 참조.

4.1 Sample quality

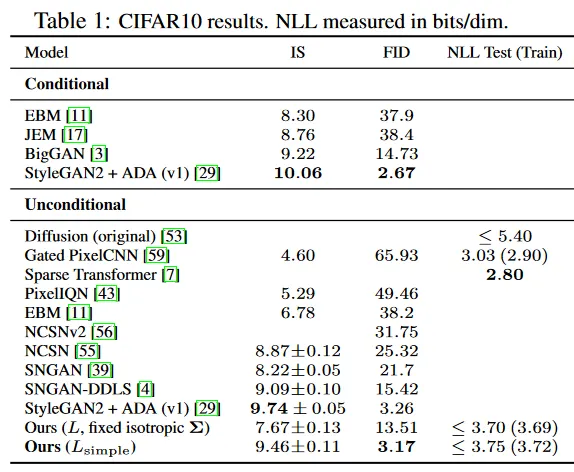
Table 1은 CIFAR10에서 Inception score, FID score와 negative log likelihood(무손실 코드길이)를 보인다. 우리의 unconditional 모델은 3.17의 FID score로 class conditional 모델을 포함하여 문헌에서 대부분의 모델 보다 더 나은 샘플 품질을 달성한다. 우리의 표준 관행을 따라 FID score를 학습 셋에서 계산했으며, 테스트 셋에서 계산할 때는 5.24 score이다. 이것은 여전히 많은 문헌에서 학습 셋 FID score 보다 낫다.
우리 모델을 실제 variational bound에서 학습하는 것이 예상대로 단순화된 목적 보다 더 나은 코드길이를 산출하지만, 후자가 최상 샘플 품질을 산출한다는 것을 발견했다. CIFA10과 CelebA-HQ 256x256 샘플에 대해 그림 1 참조. LSUN 256x256 샘플에 대해 그림 3, 4참조. 더 자세한 내용은 부록 D 참조.

4.2 Reverse process parameterization and training objective ablation

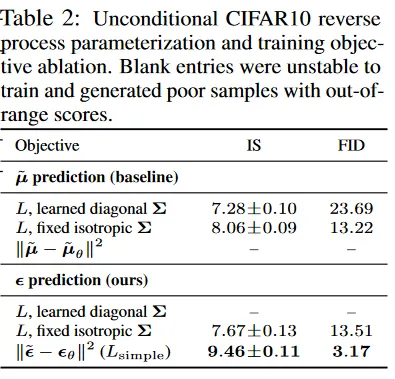
Table 2에서 reverse process 파라미터화와 학습 목적(섹션 3.2)이 샘플 품질에 미치는 영향를 본다. 우리는 μ~\tilde{\boldsymbol{\mu}}를 예측하는 baseline 옵션이 단순화된 목적(방정식 14와 유사한 unweighted mean squared error) 대신 실제 variational bound에서 학습될 때 잘 작동하는 것을 발견한다.
우리는 또한 파라미터화된 대각 Σθ(xt)\boldsymbol{\Sigma}_\theta(\bold{x}_t)를 variational bound에 통합하여 reverse process 분산을 학습하는 것이 고정된 분산과 비교하여 불안정한 학습과 더 빈곤한 샘플 품질을 이끄는 것을 발견한다. 우리가 제안한 대로 ϵ\boldsymbol{\epsilon}를 예측하는 것은, 고정된 분산과 variational bound에서 학습될 때 μ~\tilde{\boldsymbol{\mu}}를 예측하는 것과 유사하게 수행되지만, 단순화된 목적으로 학습될 때 훨씬 성능이 낫다.

4.3 Progressive coding

Table 1은 CIFAR10 모델의 코드길이를 보인다. 학습과 테스트 사이의 격차는 최대 0.03 bits/dim으로 다른 likelihood-based 모델에서 리포트된 것과 비교할만하며, 이는 우리의 diffusion model이 과적합되지 않음을 나타낸다(nearest neighbor 시각화에 대해 부록 D 참조). 우리의 무손실 코드길이가 energy-based model과 annealed importance sampling을 사용하는 score matching에 대해 리포트된 큰 추정치보다 여전히 우수하지만, 다른 likelihood-generative 모델과 비교할만하지 않다.
그래도 여전히 우리의 샘플이 높은 품질이므로 우리는 diffusion model이 훌륭한 손실 압축기를 만드는 inductive bias를 가진다고 결론 내린다. variational bound 항 L1+...+LTL_1 + ... + L_T을 rate로 L0L_0을 distortion으로 간주하면, 가장 높은 품질 샘플을 갖는 우리의 CIFAR10 모델은 1.78 bits/dim의 rate와 1.97 bits/dim의 distortion을 가지며, 이는 0에서 255의 스케일에서 0.95의 제곱근 평균 제곱 에러에 해당한다. 손실없는 코드길이의 절반 이상이 감지할 수 없는 distortion을 설명한다.
Progressive lossy compression
우리 모델의 rate-distortion 동작을 더 깊게 탐구하기 위해 방정식 5의 형식을 mirror하는 progressive lossy code를 도입한다. Algorithm 3과 4 참조. 이것들은 최소 랜덤 코딩 같은 절차에 접근할 수 있다고 가정한다. 이것은 임의의 분포 pp와 qq의 평균에 대해 DKL(q(x)∥p(x))D_{KL}(q(\bold{x})\|p(\bold{x})) 비트를 사용하여 샘플 x∼q(x)\bold{x} \sim q(\bold{x})를 전송할 수 있다. 여기서 receiver는 사전에 pp를 알고 있다고 가정한다. x0∼q(x0)\bold{x}_0 \sim q(\bold{x}_0)에 적용될 때, Algorithm 3과 4는 방정식 5와 동일한 총 기대 코드 길이를 사용하여 xT,...,x0\bold{x}_T, ..., \bold{x}_0을 순차적으로 전달한다. 임의의 시간 tt에서 receiver는 완전 사용 가능하고 점진적으로 추정할 수 있는 xt\bold{x}_t의 부분적인 정보를 갖는다.
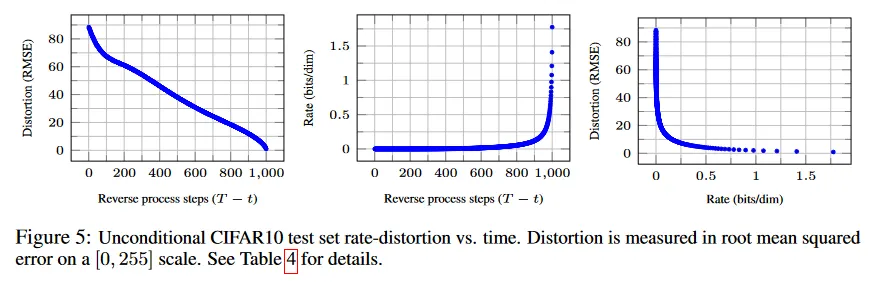
x0≈x^0=(xt−1−αˉtϵθ(xt))/αˉt(15)\bold{x}_0 \approx \hat{\bold{x}}_0 = (\bold{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_\theta(\bold{x}_t)) / \sqrt{\bar{\alpha}_t} \tag{15}
이것은 방정식 4 때문이다(확률적 reconstruction x0∼pθ(x0∣xt)\bold{x}_0 \sim p_\theta(\bold{x}_0|\bold{x}_t)도 유효하지만 이것이 distortion을 더 평가하기 어렵게 만들기 때문에 여기서 고려하지 않는다). 그림 5는 CIFAR 10 test 셋에서 rate-distortion plot 결과를 보인다. 각 시간 tt에서 distortion은 제곱근 평균 제곱 에러 ∥x0−x^0∥2/D\sqrt{\|\bold{x}_0 - \hat{\bold{x}}_0\|^2/D}로 계산된다. rate는 시간 tt까지 받은 누적 bit 수로 계산된다. rate-distortion plot의 low-rate 영역에서 distortion이 빠르게 감소한다. 이는 bit의 대부분이 실제로 감지할 수 없는 distortion에 할당된다는 것을 나타낸다.
Algorithm 3 Sending x0\bold{x}_0
1.
p(xT)p(\bold{x}_T)를 사용하여 xT∼q(xT∣x0)\bold{x}_T \sim q(\bold{x}_T|\bold{x}_0) 전송
2.
for t=T−1,..,.2,1t = T-1,..,. 2, 1 do
a.
pθ(xt∣xt+1)p_\theta(\bold{x}_t|\bold{x}_{t+1})을 사용하여 xt∼q(xt∣xt+1,x0)\bold{x}_t \sim q(\bold{x}_t|\bold{x}_{t+1}, \bold{x}_0) 전송
3.
end for
4.
pθ(x0∣x1)p_\theta(\bold{x}_0|\bold{x}_1)을 사용하여 x0\bold{x}_0 전송
Algorithm 4 Receiving
1.
p(xT)p(\bold{x}_T)를 사용하여 xT\bold{x}_T를 수신
2.
for t=T−1,...,1,0t = T-1,..., 1,0 do
a.
pθ(xt∣xt+1)p_\theta(\bold{x}_t|\bold{x}_{t+1})을 사용하여 xt\bold{x}_t 수신
3.
end for
4.
x0\bold{x}_0 반환
Progressive generation
우리는 또한 무작위 비트에서 progressive decompression으로 progressive unconditional generation 절차도 실행한다. 즉 우리는 Algorithm 2를 사용하여 reverse process에서 샘플링하면서 reverse process의 결과인 x^0\hat{\bold{x}}_0를 예측한다. 그림 6과 10은 reverse process의 코스에 대한 x^0\hat{\bold{x}}_0의 샘플 품질 결과를 보인다. 큰 이미지 feature이 먼저 나타나고, 디테일은 마지막에 나타난다. 그림 7은 다양한 tt에 대해 xt\bold{x}_t를 고정한 상태에서 확률적 예측 x0∼pθ(x0∣xt)\bold{x}_0\sim p_\theta(\bold{x}_0|\bold{x}_t)을 보인다. tt가 작을 때는 미세한 디테일을 제외한 모든 것이 보존되고, tt가 클 때는 큰 feature만 보존된다. 아마도 이것은 개념적 압축의 힌트일 것이다.
Connection to autoregressive decoding
variational bound(5)를 다음처럼 재작성할 수 있음에 유의하라.
L=DKL(q(xT)∥p(xT))+Eq[∑t≥1DKL(q(xt−1∣xt)∥pθ(xt−1∣xt))]+H(x0)(16)L = D_{KL}(q(\bold{x}_T)\|p(\bold{x}_T)) + \mathbb{E}_q\left[\sum_{t \ge 1} D_{KL}(q(\bold{x}_{t-1}|\bold{x}_t) \|p_\theta(\bold{x}_{t-1}|\bold{x}_t)) \right] + H(\bold{x}_0) \\\tag{16}
(유도는 부록 A 참조). 이제 diffusion process 길이 TT를 데이터의 차원으로 설정하고, forward process를 정의하여 q(xt∣x0)q(\bold{x}_t|\bold{x}_0)가 첫 번째 tt 좌표 mask 한 상태로 모든 확률 질량을 x0\bold{x}_0에 배치한다(즉 q(xt∣xt−1)q(\bold{x}_t|\bold{x}_{t-1})는 ttht^{th} 좌표를 masking 함). 또한 p(xT)p(\bold{x}_T)를 blank 이미지에 모든 질량에 배치하고 pθ(xt−1∣xt)p_\theta(\bold{x}_{t-1}|\bold{x}_t)는 완전히 표현력 있는 conditional 분포로 설정한다고 하자. 이러한 선택을 통해 DKL(q(xT∥p(xT))=0D_{KL}(q(\bold{x}_T\|p(\bold{x}_T)) = 0이 되고 DKL(q(xt−1∣xt)∥pθ(xt−1∣xt))D_{KL}(q(\bold{x}_{t-1}|\bold{x}_t)\|p_\theta(\bold{x}_{t-1}|\bold{x}_t))를 최소화하면 pθp_\theta는 좌표 t+1,...,Tt+1,..., T를 변경하지 않고 복사하며, 주어진 t1,...,Tt_1,...,T에 대해 ttht^{th} 좌표를 예측하도록 훈련된다. 따라서 이 특정한 diffusion을 사용하여 pθp_\theta를 학습하는 것은 autoregressive 모델을 학습하는 것과 같다.
따라서 Gaussian diffusion model(2)을 일반화된 bit ordering을 갖는 autoregressive model의 한 종류로 해석할 수 있다. 이것은 data 좌표를 reordering 하는 것으로는 표현될 수 없다. 이전 작업에서 이러한 reordering이 샘플 품질에 영향을 미치는 inductive bias를 도입한다는 것을 보였고 우리는 Gaussian diffusion이 유사한 목적을 제공한다고 추측한다. 아마도 Gaussian noise가 masking noise 보다 이미지에 더 자연스러운 추가이기 때문일 것이다. 게다가 Gaussian diffusion 길이는 데이터 차원과 동등하도록 제한받지 않는다. 예컨대 우리 실험에서 T=1000T=1000을 사용하며 이것은 32x32x3이나 256x256x3 이미지의 차원보다 훨씬 작다. Gaussian diffusion은 빠른 샘플링을 위해 짧아질 수 있고, 모델 표현력을 위해 더 길어질 수 있다.

4.4 Interpolation

우리는 qq를 확률적 encoder로 사용하여 source 이미지 x0\bold{x}_0를 latent space에서 보간할 수 있다. x0′∼q(x0)\bold{x}_0' \sim q(\bold{x}_0). 즉 xt\bold{x}_t를 xt′∼q(xt∣x0)\bold{x}_t' \sim q(\bold{x}_t|\bold{x}_0)로 샘플링한 다음 선형적으로 보간된 latent xˉt=(1−λ)x0+λx0′\bar{\bold{x}}_t = (1-\lambda)\bold{x}_0 + \lambda\bold{x}_0'를 reverse process를 통해 이미지 공간으로 decoding하여 xˉ0∼p(x0∣x~t)\bar{\bold{x}}_0 \sim p(\bold{x}_0|\tilde{\bold{x}}_t)를 얻는다. 이는 reverse process를 사용하여 소스 이미지의 오염된 버전을 선형적으로 보간할 때 발생하는 인공물을 제거하는 효과를 가진다. 그림 8(왼쪽) 참조. 우리는 λ\lambda의 다양한 값에 대해 noise로 고정하여 xt\bold{x}_t와 xt′\bold{x}_t'가 동일하게 유지되게 한다. 그림 8(오른쪽)은 original CelebA-HQ 256x256 이미지(t=500t=500)의 보간과 reconstruction을 보인다. reverse process는 고품질 reconstruction과 그럴듯한 보간을 생성하며, pose, skin tone, hairstyle, expression과 background 같은 다양한 속성을 완만하게 보간한다(안경은 제외). 더 큰 tt에서는 더 거칠고 다양한 보간이 나타나며, t=1000t=1000에서 새로운 샘플들이 생성된다. 부록 그림 9 참조.

5 Related Work

diffusion model이 flows와 VAEs와 유사해 보이지만 diffusion model은 qq에 파라미터가 없고, top-level latent xT\bold{x}_T가 데이터 x0\bold{x}_0와 0에 가까운 mutual information을 갖도록 설계되었다. 우리의 ϵ\boldsymbol{\epsilon}-예측 reverse process 파라미터화는 diffusion 모델과 denoising score matching(multiple noise level에서의 annealed Langevin dynamics 샘플링) 사이의 연결을 수립한다. 그러나 diffusion model은 log likelihood 평가를 직접적으로 허용하며, variational inference를 사용하여 Langevin dynamics 샘플러를 명시적으로 학습한다(자세한 내용은 부록 C 참조). 이 연결은 또한 특정 weighted 형식의 denoising score matching이 Langevin-유사 샘플러를 학습하기 위한 variational inference과 동일하다는 reverse 구현을 갖는다. Markov chain의 전이 연산자를 학습하는 다른 방법은 infusion training, variational walkback, generative stochastic network 등이 있다.
score matching과 energy-based 모델링 사이의 알려진 연결을 통해 우리의 작업은 energy-based model에 대한 다른 최근 작업에도 영향을 미칠 수 있다. 우리의 rate-distortion 커브는 variational bound의 한 번의 평가로 시간에 따라 계산될 수 있고, 이는 rate-distortion curve를 annealed importance sampling의 한 번의 실행에서 distortion 페널티에 따라 계산하는 방법을 연상 시킨다. 우리의 progressive decoding 논리는 convolutional DRAW와 연관된 모델에서 볼 수 있고 autoregressive model의 subscale ordering 또는 샘플링 전략에 대한 더 일반적인 설계를 이끈다.

6 Conclusion

우리는 diffusion model을 사용하여 고품질 이미지 샘플을 제시했고, diffusion model과 Markov chain을 학습을 위한 variational inference, denoising score matching과 annealed Langevin dynamics(확장하여 energy-based model), autoregressive model과 progressive lossy compression 사이의 연결을 발견했다. diffusion model이 이미지 데이터에 대한 훌륭한 inductive bias를 갖는 것으로 보이기 때문에, 우리는 다른 데이터 모달리티와 다른 유형의 생성 모델과 머신러닝 시스템의 컴포넌트로서 그들의 효용을 조사할 것이다.

Broader Impact

diffusion model에 대한 우리의 작업은 GAN, flows, autoregressive models 등의 다른 유형의 심층 생성 모델의 샘플 품질을 개선하려고 노력하는 기존 연구들과 유사한 범위를 다룬다. 우리의 논문은 diffusion model을 이러한 기술 계열에서 일반적으로 유용한 도구를 만드는데 progress를 제시하므로 생성 모델이 더 넓은 세상에 미친(그리고 미칠) 영향을 증폭시킬 수 있다.
불행히 생성 모델의 악의 적인 사용이 잘 알려져 있다. 샘플 생성 기술은 정치적 목적으로 유명 인사의 fake 이미지와 비디오를 생성하는데 사용될 수 있다. 소프트웨어 도구가 나오기 훨씬 전부터 fake 이미지가 수동으로 만들어졌지만, 우리가 만든 생성 모델은 이것을 더 쉽게 만든다. 다행히 현재 CNN으로 생성된 이미지는 검출을 가능하게 하는 미묘한 결함이 있지만 생성 모델의 개선은 이것을 더 어렵게 만든다. 생성 모델은 또한 학습에 사용된 데이터셋에서 편향을 반영한다. 많은 대규모 데이터셋이 자동 시스템에 의해 인터넷에서 수집되므로, 특히 이미지가 라벨링되지 않을 때 이러한 편향을 제거하는 것이 어렵다. 이러한 데이터셋에서 학습된 생성 모델의 샘플이 인터넷 전체에 확산되면 이러한 편향은 더욱 강화될 수 있다.
반면 diffusion model은 데이터 압축에 유용하게 사용될 수 있다. 데이터의 해상도가 높아지고 전세계 인터넷 트래픽이 증가함에 따라 광범위한 사용자들에게 인터넷의 접근성을 보장하는데 중요할 수 있다. 우리의 작업은 이미지 분류에서 강화 학습에 이르기까지 다양한 downstream task을 위해 라벨링되지 않은 raw data에 대한 representation learning에 기여할 수 있다. 또한 diffusion model은 예술, 사진, 음악 분야에서 창의적인 용도로 사용 될 수 있다.

A Extended derivations

아래는 방정식 (5)의 파생이다. diffusion model을 위한 축소된 분산 variational bound이다. 이 자료는 Sohl-Dickstein et al[53]에서 왔다. 우리는 완결성을 위해 여기서 도입한다.
L=Eq[−log⁡pθ(x0:T)q(x1:T∣x0)]=Eq[−log⁡p(xT)−∑t≥1log⁡pθ(xt−1∣xt)q(xt∣xt−1)]=Eq[−log⁡p(xT)−∑t>1log⁡pθ(xt−1∣xt)q(xt∣xt−1)−log⁡pθ(x0∣x1)q(x1∣x0)]=Eq[−log⁡p(xT)−∑t>1log⁡pθ(xt−1∣xt)q(xt−1∣xt,x0)⋅q(xt−1∣x0)q(xt∣x0)−log⁡pθ(x0∣x1)q(x1∣x0)]=Eq[−log⁡p(xT)q(xT∣x0)−∑t>1log⁡pθ(xt−1∣xt)q(xt−1∣xt,x0)−log⁡pθ(x0∣x1)]=Eq[DKL(q(xT∣x0)∥p(xT))+∑k>1DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))−log⁡pθ(x0∣x1)]\begin{align} L &= \mathbb{E}_q \left[ -\log{p_\theta(\bold{x}_{0:T}) \over q(\bold{x}_{1:T}|\bold{x}_0)} \right] \tag{17} \\ &= \mathbb{E}_q \left[ -\log p(\bold{x}_T) - \sum_{t\ge1} \log {p_\theta(\bold{x}_{t-1}|\bold{x}_t) \over q(\bold{x}_{t}|\bold{x}_{t-1})} \right] \tag{18} \\ &= \mathbb{E}_q \left[ -\log p(\bold{x}_T) - \sum_{t>1} \log {p_\theta(\bold{x}_{t-1}|\bold{x}_t) \over q(\bold{x}_{t}|\bold{x}_{t-1})} - \log {p_\theta(\bold{x}_0|\bold{x}_1) \over q(\bold{x}_1|\bold{x}_0)} \right] \tag{19} \\ &= \mathbb{E}_q \left[ -\log p(\bold{x}_T) - \sum_{t>1} \log {p_\theta(\bold{x}_{t-1}|\bold{x}_t) \over q(\bold{x}_{t-1}|\bold{x}_{t},\bold{x}_0)} \cdot {q(\bold{x}_{t-1}|\bold{x}_0) \over q(\bold{x}_t|\bold{x}_0)} - \log {p_\theta(\bold{x}_0|\bold{x}_1) \over q(\bold{x}_1|\bold{x}_0)} \right] \tag{20} \\ &= \mathbb{E}_q \left[ -\log {p(\bold{x}_T)\over q(\bold{x}_T|\bold{x}_0) }- \sum_{t>1} \log {p_\theta(\bold{x}_{t-1}|\bold{x}_t) \over q(\bold{x}_{t-1}|\bold{x}_{t},\bold{x}_0)} - \log p_\theta(\bold{x}_0|\bold{x}_1) \right] \tag{21} \\ &= \mathbb{E}_q \left[D_{KL}(q(\bold{x}_T|\bold{x}_0) \| p(\bold{x}_T)) + \sum_{k>1} D_{KL}(q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0)\|p_\theta(\bold{x}_{t-1}|\bold{x}_t)) - \log p_\theta(\bold{x}_0|\bold{x}_1) \right] \tag{22} \end{align}
다음은 LL의 대안 버전이다. 이것은 추정하기 용이하지 않지만 섹션 4.3의 논의에 유용하다.
L=Eq[−log⁡p(xT)−∑t≥1pθ(xt−1∣xt)q(xt∣xt−1)]=Eq[−log⁡p(xT)−∑t≥1pθ(xt−1∣xt)q(xt−1∣xt)⋅q(xt−1)q(xt)]=Eq[−log⁡p(xT)q(xT)−∑t≥1pθ(xt−1∣xt)q(xt−1∣xt)−log⁡q(x0)]=DKL(q(xT)∥p(xT))+Eq[∑t≥1DKL(q(xt−1∣xt)∥pθ(xt−1∣xt))]+H(x0)\begin{align} L &= \mathbb{E}_q \left[ -\log p(\bold{x}_T) - \sum_{t \ge 1} {p_\theta(\bold{x}_{t-1}|\bold{x}_t) \over q(\bold{x}_{t}|\bold{x}_{t-1})} \right] \tag{23} \\ &= \mathbb{E}_q \left[ -\log p(\bold{x}_T) - \sum_{t \ge 1} {p_\theta(\bold{x}_{t-1}|\bold{x}_t) \over q(\bold{x}_{t-1}|\bold{x}_{t})} \cdot {q(\bold{x}_{t-1}) \over q(\bold{x}_t)} \right] \tag{24} \\ &= \mathbb{E}_q \left[ -\log {p(\bold{x}_T) \over q(\bold{x}_T)} - \sum_{t \ge 1} {p_\theta(\bold{x}_{t-1}|\bold{x}_t) \over q(\bold{x}_{t-1}|\bold{x}_{t})} -\log q(\bold{x}_0) \right] \tag{25} \\ &= D_{KL}(q(\bold{x}_T)\|p(\bold{x}_T)) + \mathbb{E}_q \left[ \sum_{t\ge 1}D_{KL}(q(\bold{x}_{t-1}|\bold{x}_t)\|p_\theta(\bold{x}_{t-1}|\bold{x}_t)) \right] + H(\bold{x}_0) \tag{26} \end{align}

B Experimental details

우리의 신경망 아키텍쳐는 PixelCNN++의 backbone을 따른다. 이것은 Wide ResNet에 기반한 U-Net이다. 우리는 구현을 더 간단하게 하기 위해 weight normalization을 group normalization으로 교체한다. 우리의 32x32 모델은 4개의 feature map 해상도(32x32에서 4x4까지)를 사용하고, 256x256 모델은 6개를 사용한다. 모든 모델은 해상도 레벨 당 2개의 convolutional residual block을 갖고, 16x16 해상도에서는 convolutional block 사이에 self-attention block을 갖는다. Diffusion time tt는 각 residual block에 Transformer sinusoidal position embedding을 추가하여 지정된다. 우리의 CIFA10 모델은 35.7M 파라미터를 가지며, LSUN과 CelebA-HQ 모델은 114M 파라미터를 갖는다. 우리는 또한 filter 수를 증가시켜 약 256M 파라미터를 갖는 더 큰 LSUN Bedroom 모델을 학습했다.
우리는 모든 실험에서 TPU v3-8(8대 V100 GPU와 유사한)을 사용했다. 우리의 CIFAR 모델은 배치 크기 128에서 초당 21 step으로 학습되며(800k step에서 학습을 완료하는데 10.6시간 걸린다), 256개 이미지의 배치를 샘플링하는데 17초가 걸린다. 우리의 CelebA-HQ/LSUN (256x256) 모델은 배치 크기 64에서 초당 2.2 step로 학습되고 128개 이미지의 배치를 샘플링하는데 300초가 걸린다. 우리는 CelebA-HQ에 대해 0.5M step, LSUN Bedroom에 대해 2.4M step, LSUN Cat에 대해 1.8M step, LSUN Church에 대해 1.2M step을 학습한다. 더 큰 LSUN Bedroom 모델은 1.15M step 동안 학습된다.
초기에 네트워크 크기를 메모리 제약 내에 맞추기 위한 하이퍼파라미터 선택을 제외하고, 대부분의 하이퍼파라미터 탐색은 CIFAR10 샘플 품질을 최적화하기 위해 수행되었으며, 그 결과 설정을 다른 데이터셋에도 적용한다.
•
우리는 βt\beta_t 스케쥴을 상수, 선형, 이차 스케쥴 중에서 선택했으며 모든 LT≈0L_T \approx 0이 되도록 제한했다. 우리는 T=1000T=1000을 sweep 없이 설정하고 β1=10−4\beta_1 = 10^{-4}에서 βt=0.02\beta_t=0.02까지 선형 스케쥴을 선택했다.
•
우리는 CIFAR10에서 dropout 비율을 {0.1,0.2,0.3,0.4}\{0.1, 0.2, 0.3, 0.4\}의 값들에 대해 sweeping 한 뒤 0.10.1로 설정한다. CIFAR10에서 dropout 없을 때, unregularized PixelCNN++에서 발생한 과적합 artifacts와 유사한 더 빈곤한 샘플을 얻었다. 다른 데이터셋에서는 sweeping 없이 dropout rate를 0으로 설정한다.
•
우리는 CIFAR10 학습 중에 무작위 horizontal flip을 사용한다. flip 하는 것과 하지 않는 것을 모두 학습했지만 flip 하는 것이 샘플 품질을 약간 개선하는 것을 발견한다. 또한 LSUN Bedroom을 제외한 다른 모든 데이터셋에 대해서도 무작위 horizontal flip을 사용했다.
•
우리의 실험 과정 초기에 Adam과 RMSProp을 시도하고 최종적으로 Adam을 선택했다. 하이퍼파라미터는 표준 값으로 유지했다. learning rate를 sweeping 없이 2×10−42 \times 10^{-4}로 설정하고 256x256 이미지에서는 학습이 불안정했기 때문에 2×10−52 \times 10^{-5}로 낮췄다.
•
배치 크기는 CIFAR10에서는 128, 더 큰 이미지에서는 64로 설정했다. 이 값들을 sweep 하지 않았다.
•
모델 파라미터에 대해서는 0.9999의 decay factor로 EMA를 사용한다. 이 값들을 sweep 하지 않았다.
최종 실험은 한번 학습되고 학습 과정에서 샘플 품질을 평가했다. 샘플 품질 score와 log likelihood는 학습의 과정 중 최소 FID value을 기준으로 리포트된다. CIFA10에서 OpenAI와 TTUR 저장소의 오리지날 코드를 사용하여 50000개 샘플에서 Inception과 FID score를 각각 계산한다. LSUN에서는 StyleGAN2 저장소의 코드를 사용하여 50000개 샘플에 대해 FID score를 게산했다. CIFAR10과 CelebA-HQ는 TensorFlow 데이터셋에서 제공된 데이터를 로드하고, LSUN은 StyleGAN에서 코드를 사용하여 준비했다. Dataset 분할(또는 분할 없음)은 생성 모델링 맥락에서 처음 사용된 논문에서 제공된 표준 형식을 따랐다. 모든 세부 사항은 공개된 소스 코드에서 확인할 수 있다.
Made with