1 Overview
이전 섹션에서 representation learning의 아이디어를 논의했다. 이것은 unsupervised와 self-supervised 방법을 활용하여 고차원 sensory 데이터의 저차원 representation인 intermediate를 학습한다. 이러한 학습된 feature는 downstream 시각 추론 작업을 해결하는데 사용될 수 있다. 여기서 2가지 일반적인 computer vision 문제의 맥락에서 representation learning을 어떻게 적용되는지 살펴본다. monocular depth 추정과 feature tracking
2 Monocular Depth Estimation
2.1 Background
Depth 추정은 로보틱스에서 파지를 위한 3d reconstruction과 공간 인식 또는 자율주행 차의 네비게이션과 같은 더 복잡한 작업을 해결하는데 중요한 일반적인 computer vision 빌딩 블록이다. structured light stereo와 LIDAR(3d 포인트 클라우드)와 같은 다양한 능동적 depth 추정이 존재하지만, 여기서는 수동적 수단을 통한 depth 추정에 초점을 맞춘다. 이는 특수하고 비싼 하드웨어가 필요하지 않고, 실외 상황에서 더 잘 작동한다.
depth 추정을 computer vision의 근본적인 correspondence problem의 특별한 경우로 볼 수 있다. 이것은 3d 장면을 촬영한 여러 2d 이미지에 대한 투영된 물리적 3d 점에 해당하는 2d 위치를 찾는 것을 포함한다. 2d 프레임은 monocular 또는 stereo 카메라를 사용하여 여러 viewpoint에 의해 포착될 수 있다.
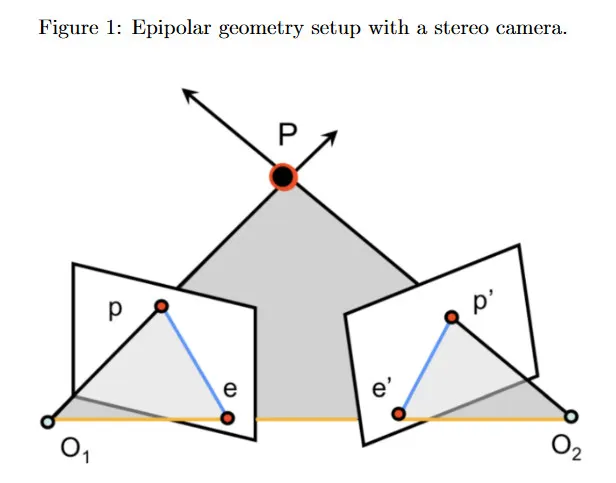
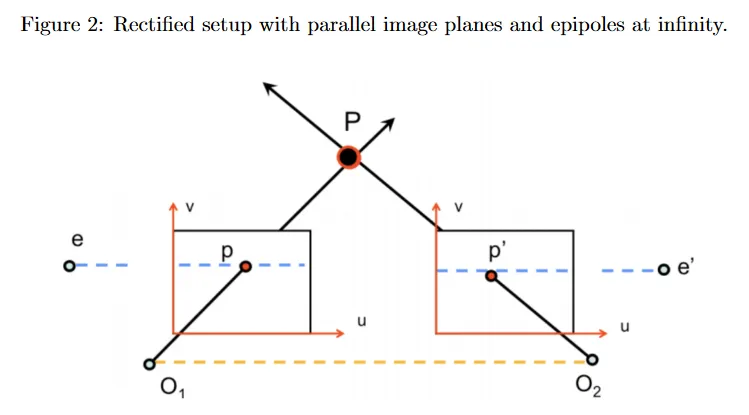
대응을 위한 한 가지 해결은 그림 1에 나온 epipolar geometry를 사용하는 것이다. 이것은 이전 강의에서 보았다. 카메라 중심 과 와 장면의 3d 점 이 주어질 때, 와 는 각각 왼쪽과 오른쪽 카메라의 이미지 평면에 가 투영된 점을 나타낸다. 왼쪽 이미지에서 가 주어지면, 오른쪽 이미지에서 대응점 는 오른쪽 카메라의 epipolar line에 어딘가에 존재해야 한다. epipolar line은 이미지 평면과 epipolar plane의 교차점으로 정의된다. 이것을 epipolar constraint라 하며 두 카메라 사이의 fundamental(또는 essential) matrix 에 의해 캡슐화된다. 가 알려진 epipolar line을 제공하기 때문이다. depth 추정의 맥락에서 종종 stereo 설정과 rectified 이미지를 다룬다고 가정한다. 이 경우 epipolar line은 수평이고 disparity(불일치)는 두 대응점 사이의 (수평) 거리로 정의된다. 즉 이고 이다. (모든 에 대해 임에 유의하라)
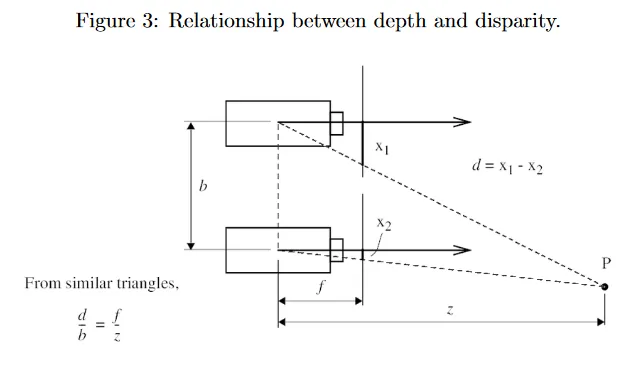
그러면 disparity와 depth 사이에 간단한 반비례 관계가 있음을 볼 수 있다. 이것은 카메라 중심에 대한 의 -좌표로 정의된다. 그림 3에 나온대로 유사 삼각형을 사용하여 을 얻을 수 있다. 여기서 는 카메라의 focal length(초점 거리)이고 는 두 카메라 사이의 baseline 길이(그림 2에서 노란 점선)이다. 와 카메라 intrinsic 가 알려졌다고 가정하면, 그림 2에 그려진대로 두 rectified 이미지 사이의 대응점을 찾을 수 있고 그들의 disparity와 depth를 알 수 있다. 에 대한 대응점 를 식별하는 한가지 접근은 다른 이미지에서 epipolar line을 따라 간단한 1d 검색을 수행하여 픽셀 또는 패치 유사성을 사용하여 가장 가능한 의 위치를 결정하는 것이다. 그러나 이런 순진한 접근은 현실 세계 이미지에서 occlusion, repetitive 패턴과 homogeneous region(즉, texture의 부재)과 같은 이슈를 겪을 수 있다. 대신 현대의 representation learning 방법을 사용한다.
2.2 Supervised Estimation
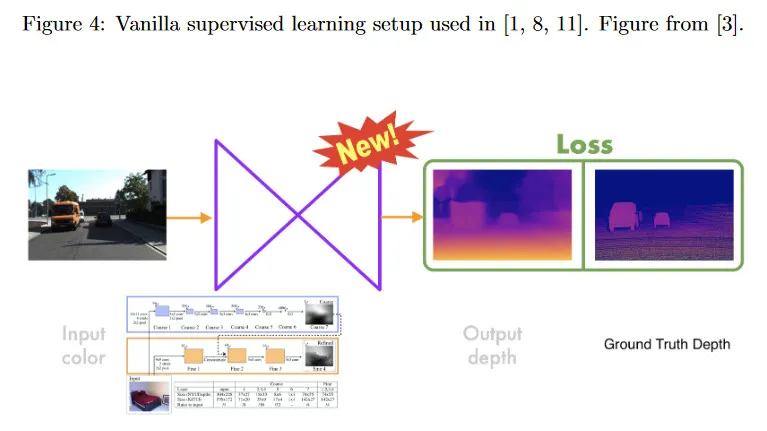
여기서 monocular (single-view) depth estimation의 작업에 초점을 맞춘다. 우리는 테스트 시간에 가능한 단일 이미지만 사용하고 장면 내용에 대한 어떤 가정도 하지 않는다. 반면 stereo(multi-view) depth estimation 방법은 여러 이미지를 사용하여 추론을 수행한다. monocular depth estimation은 under-constrained 문제이다. 즉 기하학적으로 이미지에서 각 픽셀의 깊이를 결정하는 것이 불가능하다. 그러나 인간은 perspective, scaling, 조명과 차폐를 통한 appearance 같은 단서를 활용하여 하나의 눈만으로도 깊이를 잘 추정할 수 있다. 그러므로 이런 단서를 활용하면 컴퓨터도 단일 이미지만으로 깊이를 추론할 수 있어야 한다. 그림 4에 나온 fully supervised learning 방법은 학습 모델(CNN)에 의존하여 ground truth depth와 RGB 카메라 프레임의 쌍에 대한 픽셀별로 disparity를 예측한다.학습 loss는 예측과 ground-truth depth 사이의 유사성을 포착하고 이 손실을 최소화하는 것에 초점을 맞춘다. monocular 방법은 depth를 scale까지만 포착할 수 있기 때문에 [1]은 기존의 monocular 방법에 대해 scale-invariant error를 사용할 것을 제안한다.
2.3 Unsupervised Estimation
supervised learning 방법이 괜찮은 결과를 달성했지만, 이 방법들은 대량의 ground depth 데이터가 존재하는 장면 유형에만 제한된다. 이는 입력 RGB 프레임 데이터와 알려진 intrinsic을 갖는 stereo 카메라만 요구하여 값비싼 라벨링 효과를 피할 수 있는 unsupervised 학습 방법에 동기를 부여한다. 여기서는 사례 연구로써 [3]에서 제안된 접근을 조사한다. reconstructed와 ground truth depth사이의 차이를 loss로 사용하는 대신 unsupervised formulation은 autoencoder를 사용하여 입력 reference image와 reconstructed version 사이의 차이를 최소화하는 이미지 reconstruction으로 문제를 변환한다.
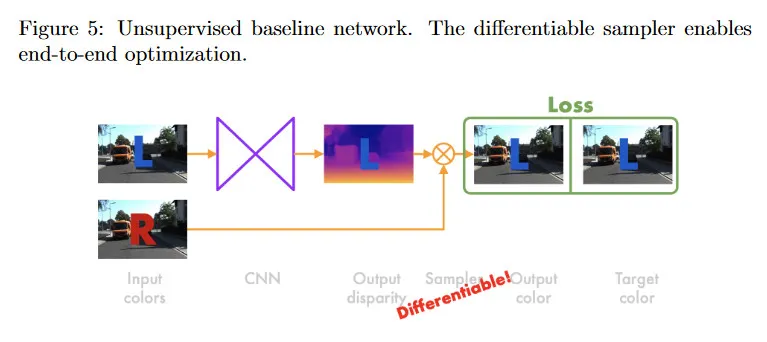
그림 5에 보여지는 baseline 네트워크는 왼쪽 이미지 만 재구성한다. 네트워크에 대한 입력은 왼쪽 프레임 이다. CNN은 왼쪽 프레임을 오른쪽 이미지 을 왼쪽으로 warp하는데 필요한 disparity(displacement) 값 로 매핑한 다음, disparity 값을 intermediate representation으로 사용하여 오른쪽 이미지에서 샘플링하여 왼쪽 이미지 를 재구성한다. 로 오른쪽 이미지에서 샘플링할 수 있지만 는 정수가 아니므로 정확한 새로운 위치에서 픽셀은 존재하지 않을 수 있다. 네트워크를 학습하기 위해 end-to-end 최적화를 수행하려면 fully (sub-) 미분가능한 bilinear 샘플러를 사용한다.
네트워크를 학습하기 위해 왼쪽과 오른쪽 이미지를 모두 사용하지만 테스트 시간에 left-aligned depth를 추론하는데 왼쪽 이미지만 필요하다. 네트워크 아키텍쳐는 fully convolutional으로 구성되며, encoder 다음에 decoder가 따르는 구성으로 double spatial scale에서 여러 disparity 맵을 출력한다. 예를 들어 첫 번째 disparity map의 해상도가 라면, 두 번째 disparity map의 해상도는 가 될 수 있다.
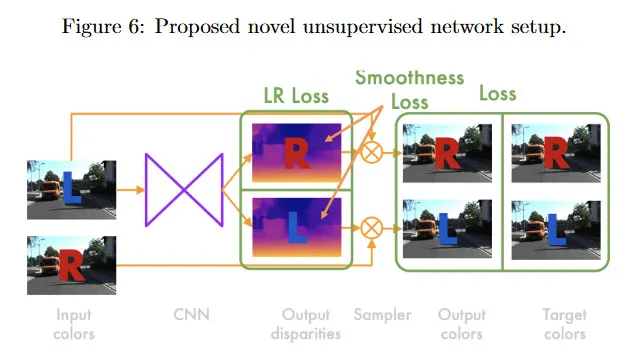
baseline을 너머 [3]은 왼쪽과 오른쪽 frame을 모두 재구성하는 새로운 아키첵쳐를 제안한다. 이것은 그림 6 참조. disparity의 이미지 품질을 개선하기 위해 더 복잡한 손실항을 도입할 수 있게 한다.
CNN은 입력에서 왼쪽 프레임 을 취하고 left-aligned disparity 과 right-aligned disparity 을 계산한다. right-aligned disparity 맵은 왼쪽 프레임에서 오른쪽 프레임을 reconstruct하기 위해 필요한 horizontal displacement 값을 포함한다. 이전에서 샘플러를 사용하여 에서 과 에서 을 reconstruct하고 왼쪽과 오른쪽 입력 이미지와 reconstructed 이미지 모두 사이의 loss를 계산한다(전체 4개 이미지). total loss 는 각 scale 에서 loss의 합이다.
3개의 컴포넌트가 있음을 볼 수 있다. 각각은 front에 scaling factor와 left, right에 변형을 갖는다. 따라서 다음 방정식들은 왼쪽 reconstructed 이미지에 대한 절차를 설명하지만, 오른쪽 이미지에 대해서도 대신 을 사용하여 동일한 방법에서 항을 계산할 수 있다.
첫 항 는 reconstruction loss이다.
이것은 위치 에서 모든 픽셀을 통해 반복하고 다음의 weighted 결합을 계산한다. 1) reconstructed와 ground truth image 사이의 L1 차이와 2) 각 픽셀에서 중심으로 한 두 대응 패치 사이의 유사도를 패치의 luminance, contrast, structure의 결합을 통해 계산하는 negative Structural Similarity Index(SSIM). 그 다음 평균을 취한다. 논문에서는 를 사용했으므로 SSIM은 L1 차이보다 더 강조되었다.
다음으로 두 번째 항 는 smoothness loss이다.
이 loss가 다시 모든 픽셀 를 통해 반복하며 disparity map의 와 방향 모두에서 gradient()에 페널티를 부여하는 것을 볼 수 있다. 이것은 disparity의 abrupt(급격한) 변화(high gradient)를 줄이는 효과를 갖고, 결과적으로 더 smooth한 disparity map을 만든다. 그러나 특정 depth에서 하나의 객체에서 다른 depth의 또 다른 객체로 translation 할 때 객체 edge에 높은 disparity를 원할 수 있다. 이것을 고려하기 위해, 원본 이미지에서 edge를 검출하면 smoothness 페널티를 완화한다. image gradient가 높으면 은 작아진다. 이미지 gradient의 L2를 취하지만, disparity map gradient에 대해서는 L1을 사용한다는 점에 유의하라.
마지막으로 3번째 항 은 left-right consistency loss이다.
여기서 직관은 두 이미지 평면에서 대응하는 픽셀 사이의 절대 거리, 즉 disparity는 오른쪽에서 왼쪽으로 계산하든 왼쪽에서 오른쪽으로 계산하든 동일해야 한다는 것이다. 그러므로 네트워크에서 출력된 왼쪽과 오른쪽 이미지에 대한 예측된 disparity 사이의 차이에 페널티를 부여한다. 이것을 달성하기 위해 각 픽셀 를 반복하고 left-aligned disparity 와 해당하는 right-aligned disparity 사이의 L1 거리를 계산한다. 여기서 이미지가 아니라 disparity map을 샘플링하는데 disparity를 사용하는 있다는 것에 유의하라. 결과적으로 저자들은 이 unsupervised 설정이 baseline과 기존 최신 fully supervised 방법 모두를 능가함을 보였다.
2.4 Self-Supervised Estimation
depth 추정을 위한 unsupervised 방법 이후에 self-supervised learning이 등장했다. 여기서는 후속 논문 [4]를 리뷰한다.
이 방법에서 depth 추정 문제를 새로운 view 합성 문제로 프레임화 한다. 장면의 타겟 이미지가 주어지면 학습된 파이프라인은 다른 viewpoint에서 장면이 어떻게 보일지 예측하는 것을 목표로 한다. Depth는 새로운 view를 얻기 위한 intermediate representation으로 사용되므로, 테스트 시간에 다른 작업에서 사용하기 위해 pipeline에서 depth map을 추출할 수 있다. monocular 설정에서는 monocular 비디오를 지도 신호로 사용한다. 대상 이미지는 시간 에서 컬러 프레임 이고 다른 viewpoint의 이미지 또는 source view는 시간적으로 인접한 프레임 이다. 전체 원래 입력을 reconstructing하는 대신 현재 입력에서 미래와 과거 입력을 예측하므로, 이것은 self-supervised learning의 예이다.
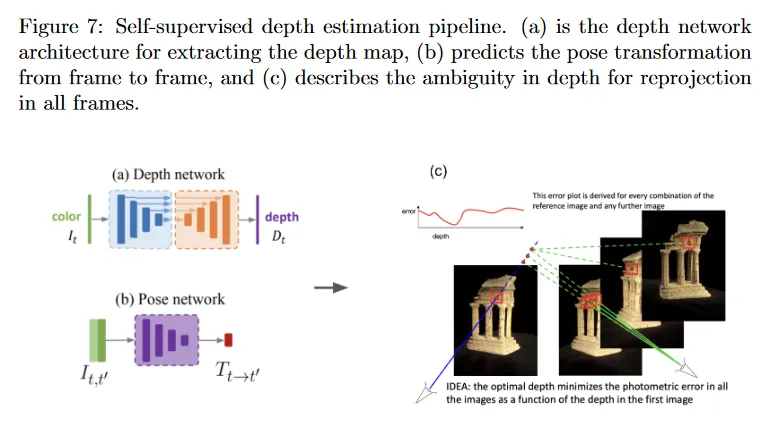
pipeline은 그림 7에 설명된다. 우선 intermediate depth representation을 얻는다. 색상 입력 가 주어지면 convolution encoder-decoder 아키텍쳐를 통해 실행하여 그림 7a에 보여지는 depth map 를 얻는다. 동시에 그림 7b에서 보여지는대로 과거와 미래의 source 프레임 를 반복하여 에서 로 변환을 나타내는 상대 포즈 를 계산한다. 모든 타겟과 source view에 대해 동일한 카메라 intrinsic 를 가정하면, 그림 7c에 보이는대로 reprojection을 통해 에 대한 새로운 view를 얻을 수 있다. 모든 픽셀에 대한 와 예측된 depth 가 주어지면, 특정 2d 이미지 좌표 를 3d 점 위치로 backproject 할 수 있다. 상대 포즈 를 알기 때문에, source view의 이미지 평면 에서 3d 점을 project하여 새로운 이미지 평면 에서 2d 좌표 를 얻을 수 있다. monocular 비디오를 가지므로 ground truth 는 알려져 있다. 따라서 에 대한 합성된 view는 가 된다. 합성된 view 와 ground truth view , 사이의 이미지 패치는 시각적으로 유사해야 하며, 이것은 다음과 같이 정의되는 photometric error에 의해 측정된다.
photometric error는 모든 2d 좌표에 대한 reproejction error 를 최소화하는 최적의 depth map 를 찾는다. 그 다음 의 쌍에 대한 photometric error를 합산한다. 여기서
이전 논문과 유사하게 방정식 5의 photometric error는 structural similarity index와 L1 차이의 weighted 결합이다. 결과적으로 저자들은 이 self-supervised 설정이 기존 unsupervised와 다른 self-supervised 접근을 능가함을 보였다.
3 Feature Tracking
(목차가 잘못된 듯. 내용 없음)
4 Motivation
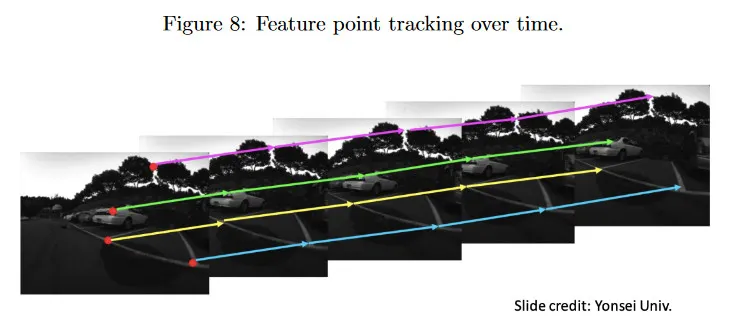
이미지의 시퀀스가 주어지면 feature tracking 작업은 모든 이미지에 걸쳐 2d 점의 집합의 위치를 추적하는 것을 포함한다. 그림 8 참조. depth 추적과 유사하게 feature tracking을 이미지 시퀀스 전체에 걸쳐 대응 문제를 해결하는 또 다른 인스턴스로 볼 수 있다.
feature tracking은 장면에서 객체의 움직임을 추적하는데 사용될 수 있다. 우리는 장면 내용이나 카메라 움직임에 관한 어떤 가정도 만들지 않는다. 카메라는 움직일 수도 있고 고정될 수도 있고, 장면에는 여러 움직임이나 정적 객체를 포함할 수 있다.
feature tracking의 도전은 프레임 간에 효율적으로 추적할 수 있는 feature point를 식별하는 것이다. 카메라가 움직임(feature는 완벽하게 사라질 수 있음), 그림자, 차폐 때문에 이미지 feature의 외관이 프레임에 걸쳐 드라마틱하게 변경될 수 있다. feature tracking을 위한 외관 모델이 업데이트 되면서, 작은 에러가 누적되어 drift가 발생할 수 있다. 우리의 목표는 쉽고 일관되게 추적할 수 있는 distinct region(feature 또는 때때로 keypoint라 불림)을 식별한 다음, 간단한 추적 방법을 적용하여 이러한 대응점을 지속적으로 찾는 것이다.
전통적으로 추적하기 쉬운 이미지 내의 distinct feature는 hand-designed 방법 [5, 10, 9, 12, 7]을 사용하여 검출되고 추적되었다. 구체적으로 이러한 좋은 feature는 다른 이미지의 feature와 빠르게 매칭할 수 있도록 소위 descriptor라 불리는 것으로 인코딩된다. 즉, 대응점을 찾는 것이다. 이러한 방법은 또한 희소하여, 이미지에서 일부 픽셀에 대해서만 descriptor를 생성한다. 이 섹션에서는 hand-designing 하는 대신, representation learning을 사용하여 이미지 feature의 descriptor를 학습할 수 있는 방법을 살펴본다.
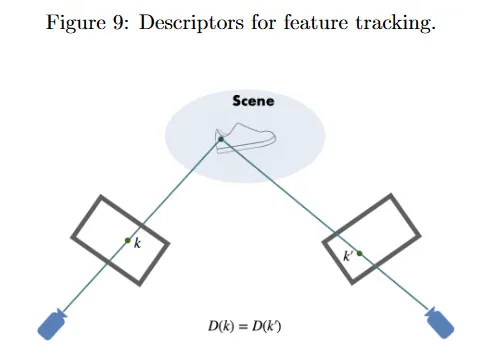
그림 9에서 는 픽셀 의 -차원 표현을 제공한다(종종 이웃 정보를 통합함). 가 동일한 3d 점에 해당하므로, 이들이 시각적으로 유사할 것이라고 기대하며, 따라서 서로 다른 viewpoint에서 포착되었더라도 그들의 descriptor는 동일해야 한다. 즉, 이어야 한다. 그 다음 descriptor 사이의 유사성에 기반하여 서로 다른 프레임의 픽셀을 매칭할 수 있다.
5 Learned Dense Descriptors
[2]에서 제안한 dense descriptor를 학습하기 위한 방법을 조사한다.
컬러 이미지가 주어지면, 우리는 컬러 이미지에서 모든 픽셀에 대한 -차원 descriptor를 출력하는 매핑 을 학습하기를 원한다. 여기서 ‘Dense’는 입력 이미지의 모든 점에 descriptor가 있다는 것을 의미하며, 단지 sparse 집합만 있는 것이 아니다. 그림 10에서 시각화 목적으로 -차원 descriptor는 차원 축소를 통해 RGB로 매핑된다. 실제로 는 convolutional encoder-decoder 아키텍쳐를 가진 학습된 신경망이다. 이 신경망은 서로 다른 view 에서 동일한 객체의 이미지의 쌍을 사용하여 pixel-contrasitve loss로 학습된다. 이것은 유사한 descriptor 사이의 거리를 최소화하고 다른 descriptor 사이의 거리를 최대화하여 픽셀에서 contrast를 반영하려고 한다.
우리는 이미지 쌍에 대한 대응점의 목록(여기서 match라고 부름)이 주어진다고 가정한다. 우리는 네트워크를 실행하여 이미지에서 모든 점에 대한 descriptor를 계산한다. 각 ground truth 매치에 대해 두 대응점에서dml descriptor 사이의 L2 거리를 계산한다. 우리는 descriptor 공간에서 거리 를 최소화하기를 원한다.
contrastive part에 대해 non-matches(서로 대응하지 않는 점들의 쌍)에 대한 loss 항도 계산한다. 여기서 non-corresponding 점 사이의 거리를 최대화 하기를 원한다( 연산은 이 거리를 최대 거리 까지 최대화한다), 이는 다음과 같이 주어진다.
에 대한 실제 대응점이 알려진다고 가정하면, non-matches의 쌍을 쉽게 찾을 수 있다. 단순히 에서 대응점이 아닌 임의의 점을 샘플링할 수 있다. 그림 12에서 는 non-matched 점을 나타내는 반면 그림 7에서 는 matched point를 나타낸다는 점에 유의하라. 그러면 total loss는 두 개의 합이다.
최소한의 인간의 도움으로 대규모로 ground truth 대응점을 저렴하게 얻는 것에 있다. 이를 위해 저자들은 자율적이고 self-supervised 데이터 수집을 수행하기 위해 로보틱스 설정을 사용할 것을 제안한다.
고정된 객체의 다양한 포즈에서 이미지를 포착하기 위해 로봇 팔이 사용된다. 그림 13 참조. 이 정밀한 로봇 팔의 forward kinematics가 알려지기 때문에 카메라 포즈와 해당하는 view의 일치된 쌍을 갖는다. 모든 view를 사용하여 3d reconstruction은 수행하여 객체의 3d 모델을 얻는다. 카메라 포즈, 3d 점 그리고 이미지를 사용하여 이제 우리가 원하는만큼 많은 ground-truth 대응점을 생성할 수 있다. 네트워크는 방정식 9를 사용하여 학습되고 background randomization, data augmentation과 hard-negative scaling과 같은 몇 가지 다른 트릭과 결합하여 사용된다.
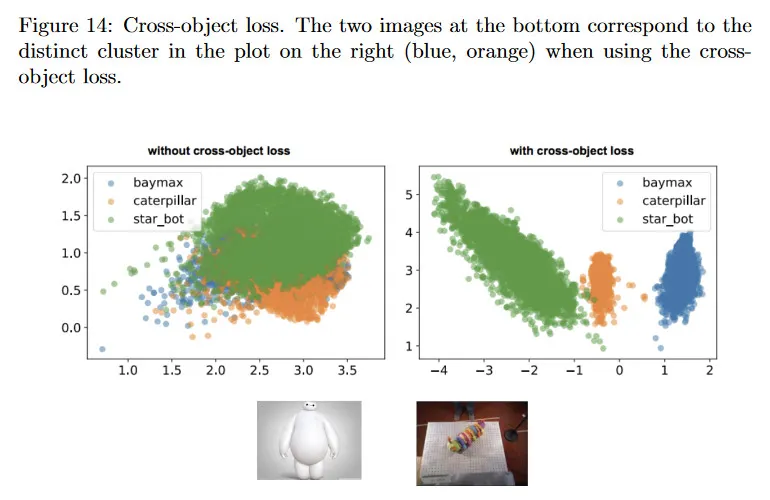
만일 동일한 객체의 쌍에 대해서만 학습하면, 다양한 객체에 대해 학습된 descriptor들이 완전히 다른 entity에 해당함에도 불구하고 겹치게 된다. 만약 cross-object loss(두 개의 서로 다른 객체의 이미지에서 나온 픽셀이 모두 non-match인)를 포함하면, descriptor 공간에서 뚜렷한 클러스터가 형성되는 것을 볼 수 있다. 그림 14 참조.
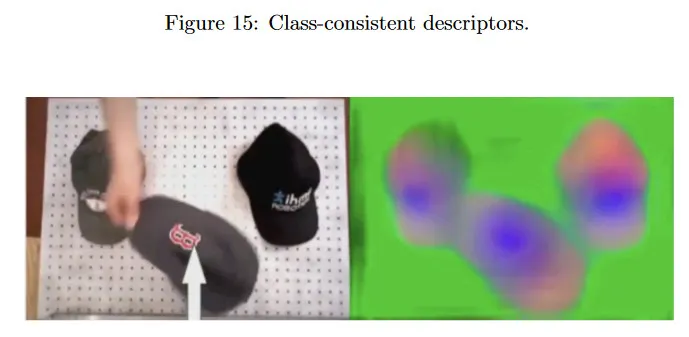
반면에 동일한 클래스의 객체들이 시각적 외관이 다르더라도 유사한 descriptor를 나타내기를 원한다. 우리의 네트워크가 이를 학습하는 능력이 있음을 보인다. 그림 15. 모자들은 색상과 디자인이 다르지만, 그들의 descriptor는 동일한 구조와 색상을 공유한다.