•
이전에 들었던 유사한 부분이 많기 때문에 간략히 정리. backpropagation 계산 등에 대한 상세 내용은 아래 페이지 참조
•
지금까지 배운 내용 요약
•
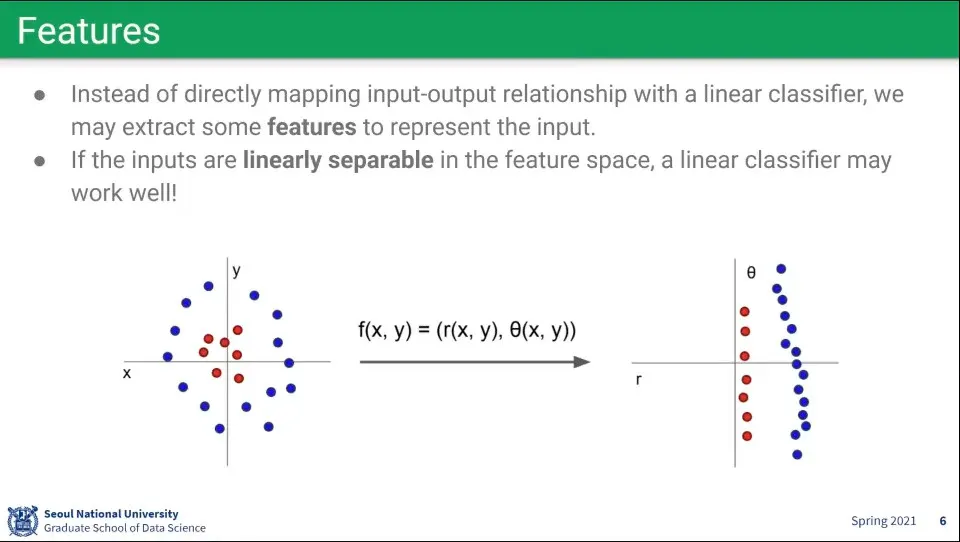
선형 함수는 위와 같이 비선형 문제를 풀 수 없다는 한계가 있다.
•
비선형 데이터를 오른쪽처럼 선형으로 변환해서 선형 함수를 적용할 수 있을까?
◦
모든 문제가 그렇게 되지는 못 함
•
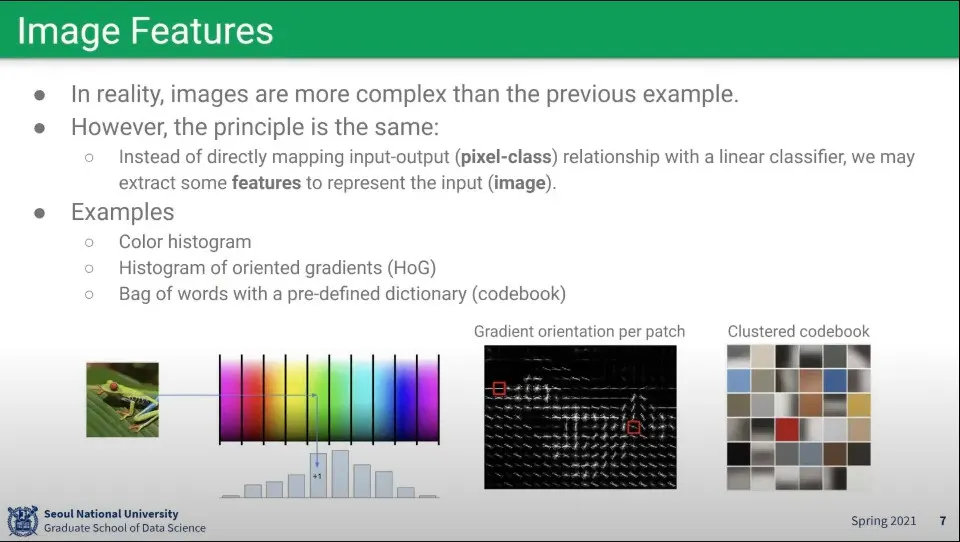
이미지에서 어떤 특징(feature)를 뽑고, 그것들을 이용해서 모델링을 하자.
◦
위 예는 과거의 방법
•
그래서 feature를 뽑은거 갖고(pre-extracted) 학습을 시키고, 그걸 학습하면 되지 않을까?
•
하지만 feature를 뽑는 것 자체도 machine learning에 맡기자는 생각으로 end-to-end 학습이 대두되었고 대세가 됨.
•
하지만 이것은 너무 많은 데이터가 필요하고 연산이 많이 필요하다는 문제가 있음
•
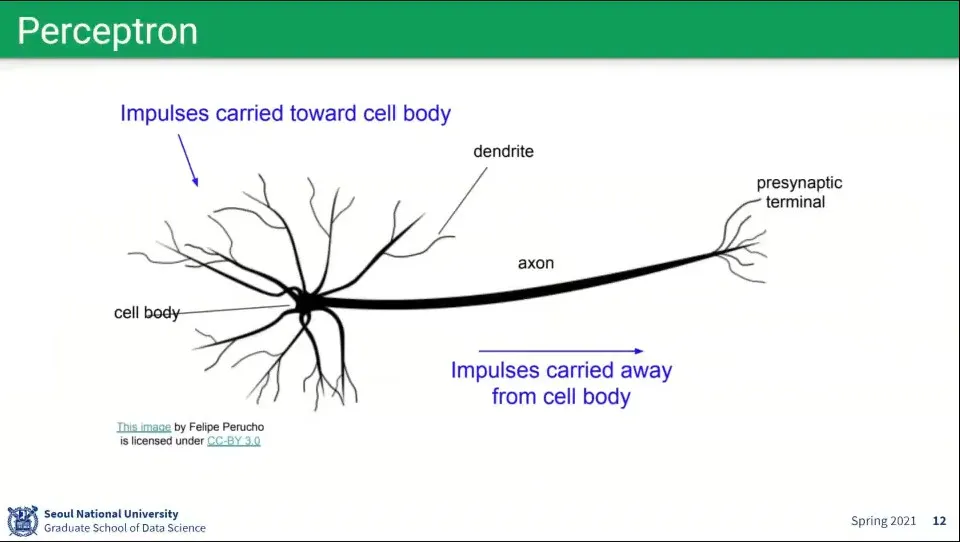
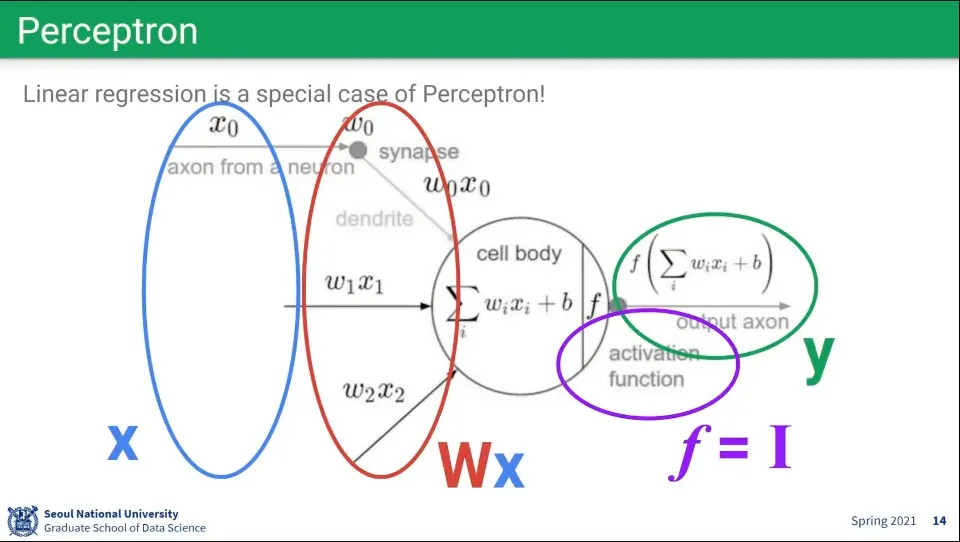
뉴럴 네트워크에서 사용하는 퍼셉트론은 뇌 뉴런의 모습을 모사하여 구성함
◦
input들을 합쳐서(활성화 함수) threshold를 넘기면 output을 내보냄
•
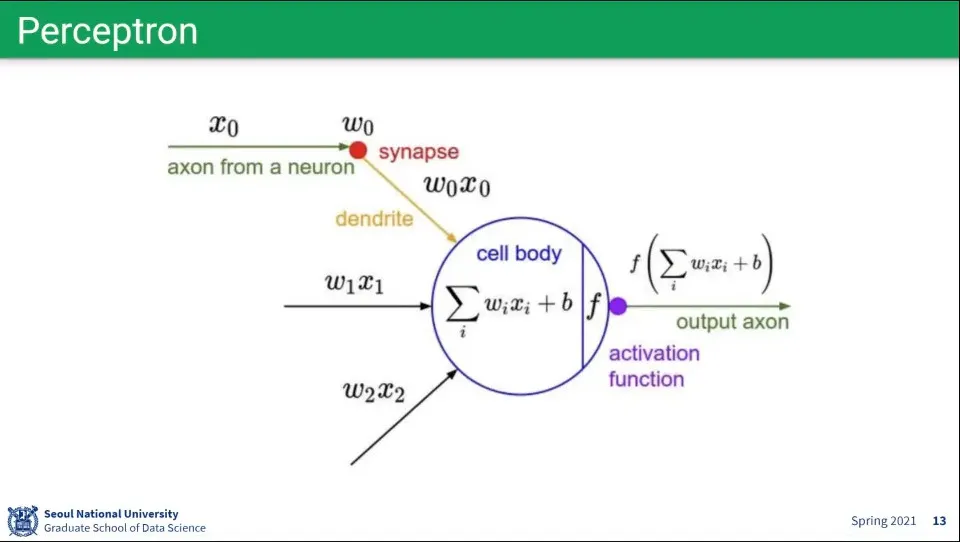
퍼셉트론을 수학적으로 표현하면 위와 같다.
•
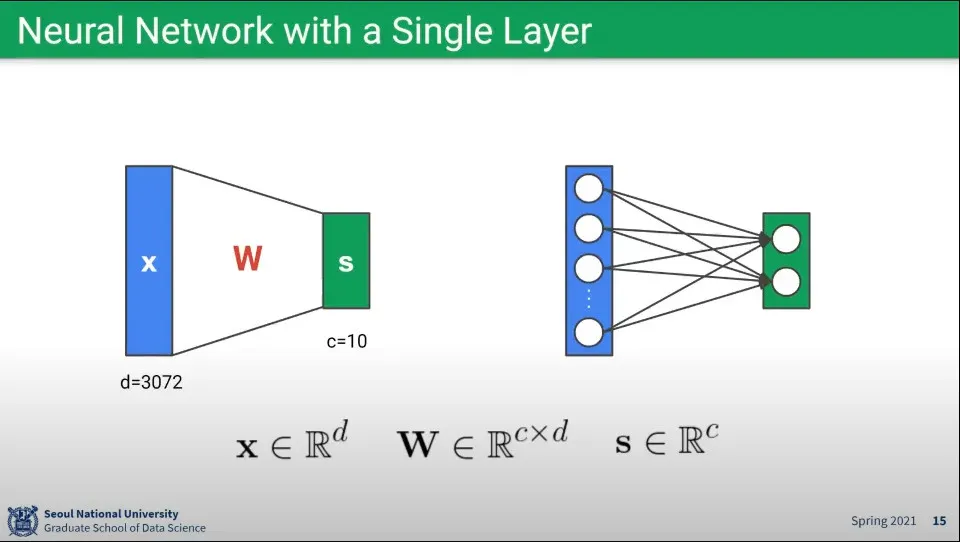
뉴럴 네트워크를 단일 레이어로 구성하면 위와 같다.
•
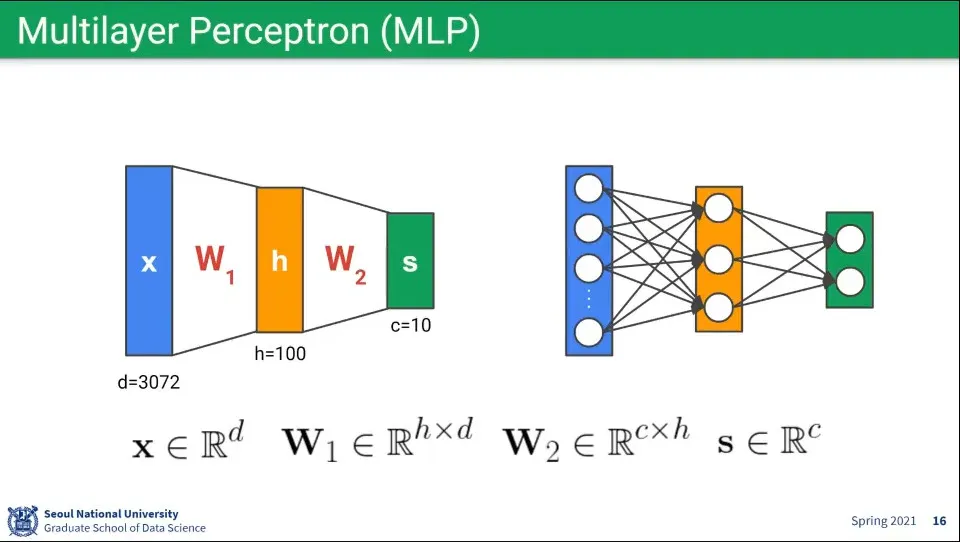
뉴럴 네트워크가 여러 레이어로 되어 있다면 위와 같다.
•
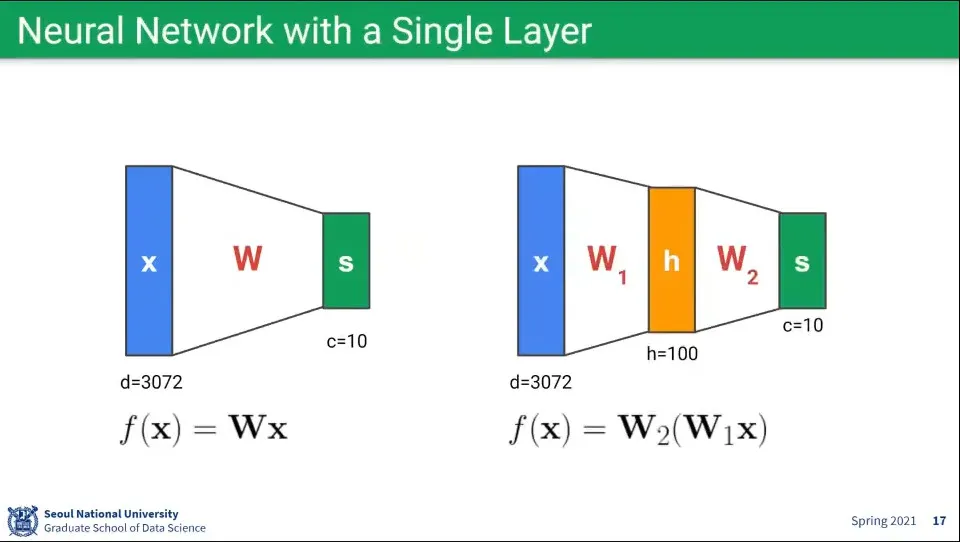
수학적으로 행렬 연산이기 때문에 단일 레이어나 멀티 레이어나 완전 동일함
•
단일 레이어나 멀티 레이어의 차이를 만들어주는게 activation function
•
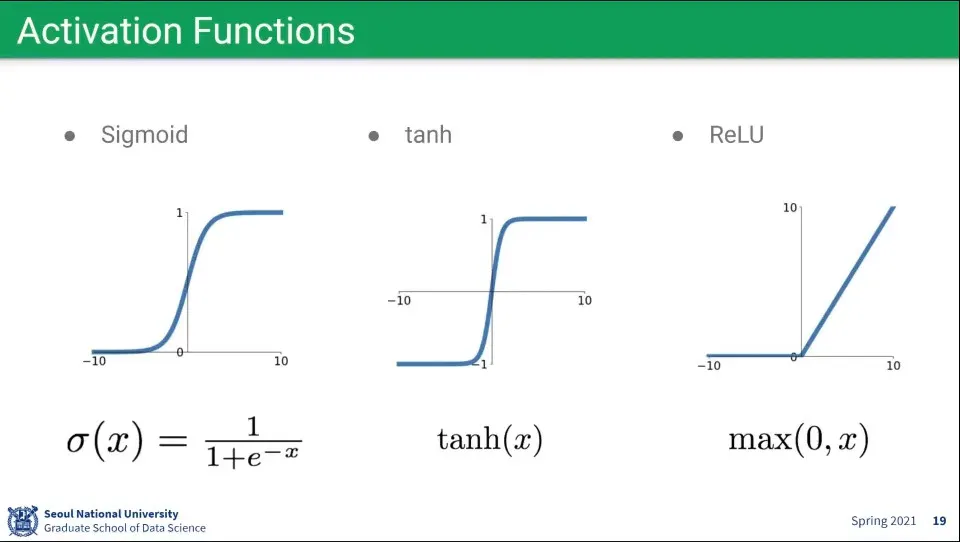
활성화 함수로는 Sigmoid, tanh, ReLU 등을 많이 사용한다.
•
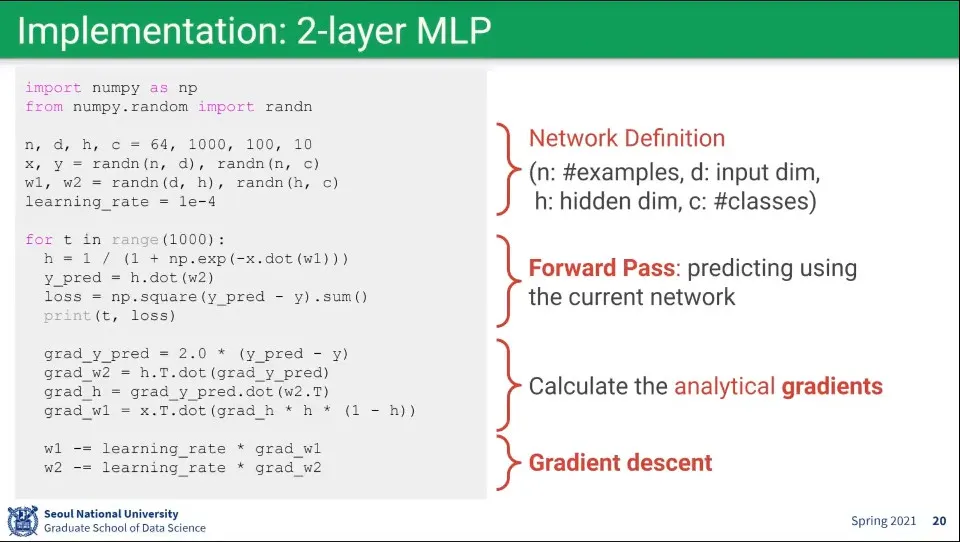
멀티 레이어를 코드로 짜면 위와 같다.
•
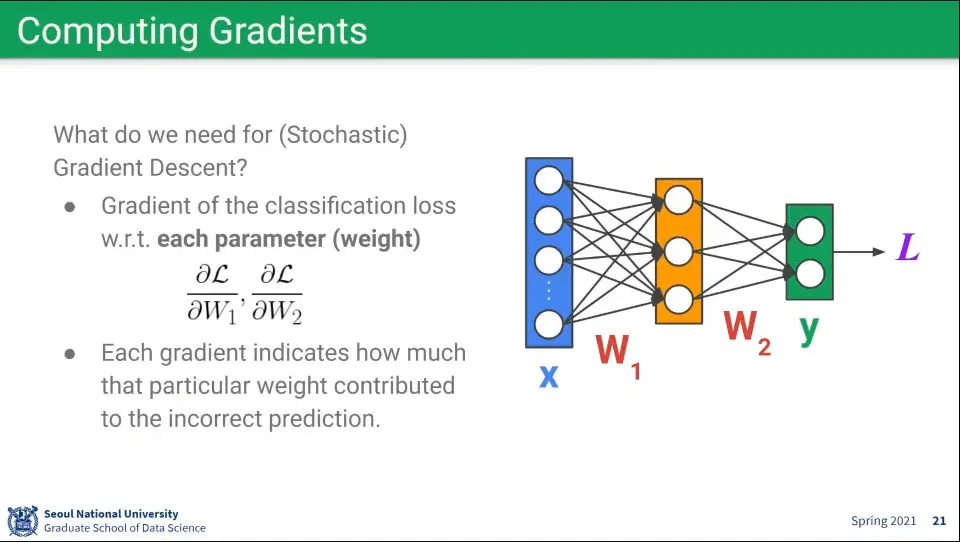
Gradient는 Loss를 기준으로 계산 함
•
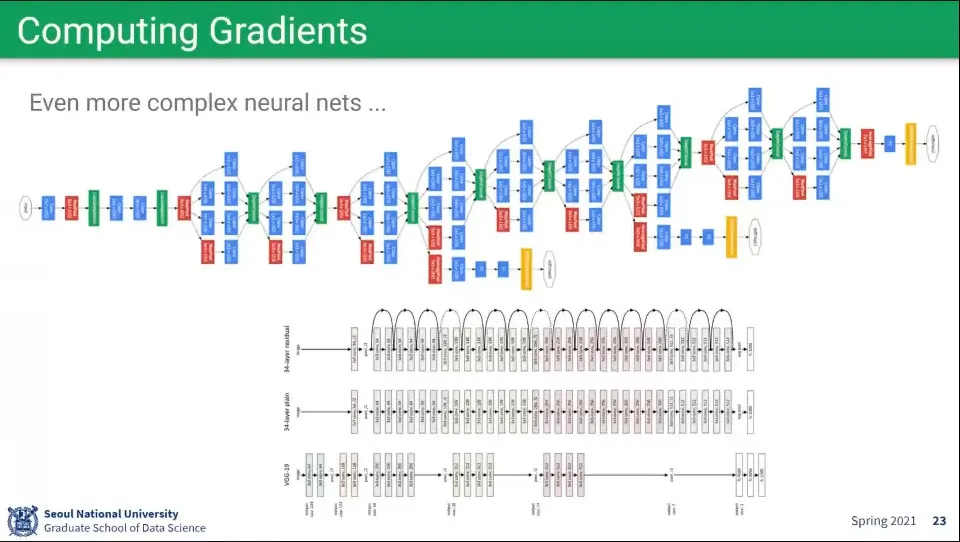
그런데 현재의 모델은 너무 복잡해서 사람이 직접 계산하기 어렵다.
•
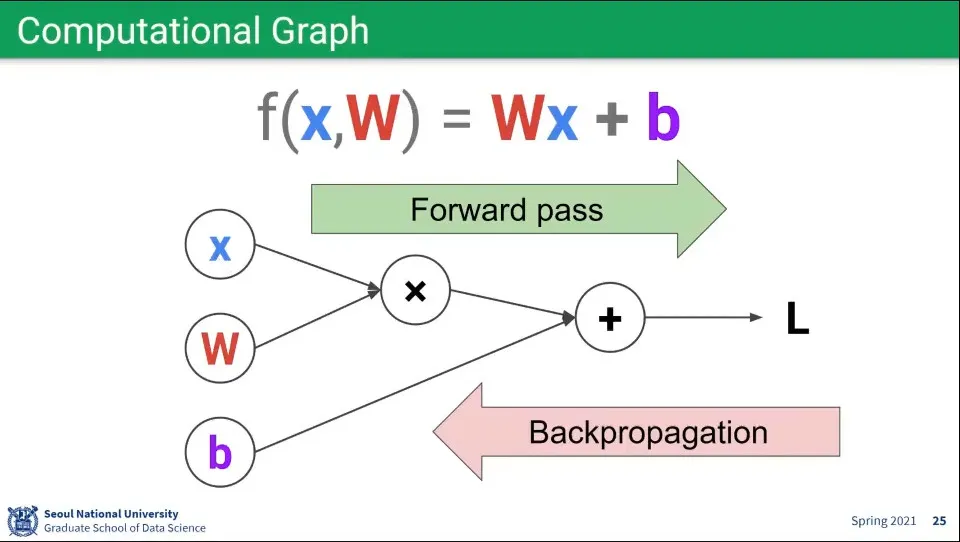
뉴럴 네트워크는 Computational Graph로 표현할 수 있다.
◦
이때 Forward pass는 이 값을 계산하는 것이라 할 수 있고
◦
Backpropagation은 각각의 값들이 Loss에 얼마나 기여를 했는지를 계산하는 것이라 할 수 있다.
•
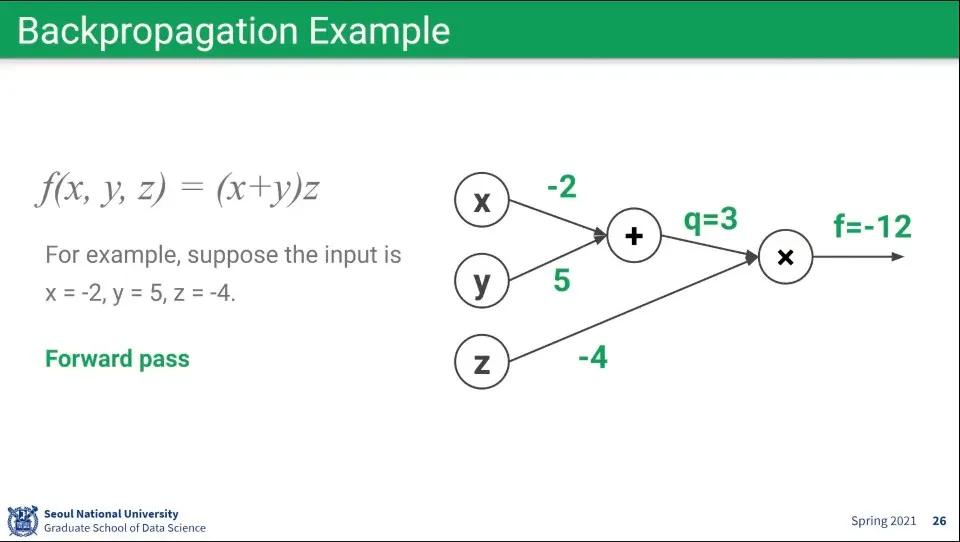
Forward pass 계산 예. 조건이 위와 같을 때 위와 같이 계산된다.
•
Backpropagation 예
◦
가장 오른쪽의 Loss에서부터 거꾸로 편미분을 하면서 계산한다. Loss는 자기 자신을 편미분 하는 것이라 값은 항상 1이 되고, 그걸 기반으로 Backpropagation을 계산한다.
•
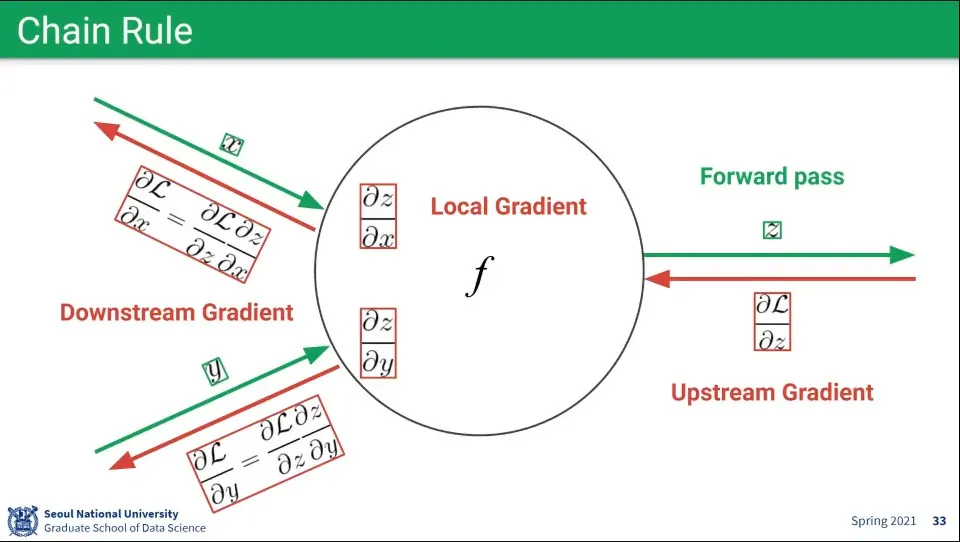
Chain Rule 설정
◦
노드의 Gradient는 Local Gradient라고 하고, 다음 노드의 Gradient는 Upstream Gradient이라 하고 이전 Gradient는 Downstream Gradient라고 한다.
◦
Backpropagation은 다음 노드에서부터 거꾸로 계산되는데, 이때 현재의 편미분은 다음 노드의 편미분을 이용해서 계산할 수 있다. 이것을 Chain Rule이라고 함.
•
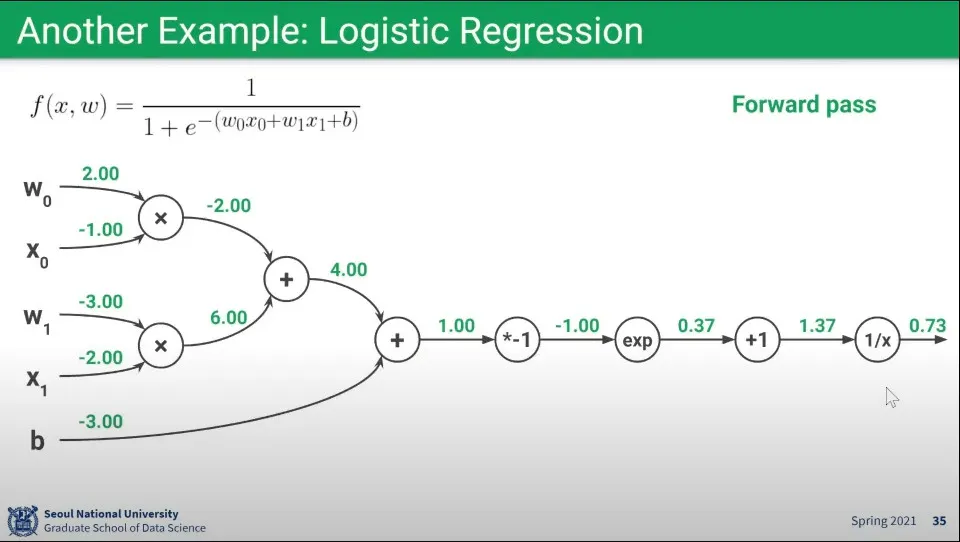
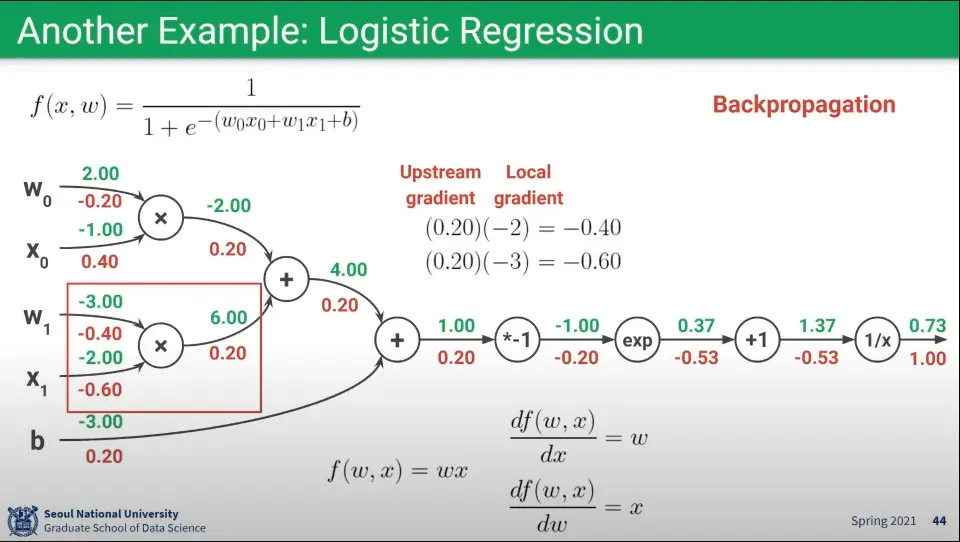
Logistic Regression에 대한 Forward pass 예
•
위 함수의 Backpropagation 예
•
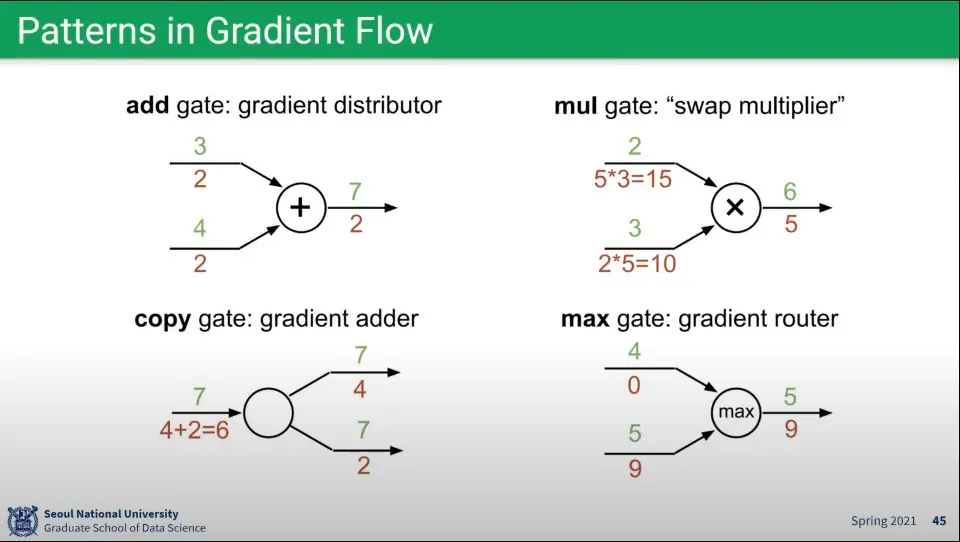
위와 같은 Gradient 계산에는 패턴이 존재한다.
◦
더하기 연산 - Backward에서 Upstream의 값을 같이 받음
◦
곱하기 연산 - Backward에서 반대편의 값을 Upstream에 곱해서 받음
◦
복사 연산 - Backward에서 Upstream들의 값을 더해서 받음
◦
Max 연산 - Foward일 때 Max였던 것만 Backward에서 값을 받고, 그렇지 않은 것은 0을 받음
•
앞선 예에 대한 코드 구현
•
앞선 예는 scalar에 대한 것이었는데, vector와 matrix에 대해 동일하게 계산 가능하다.
◦
다만 좀 복잡할 뿐
•
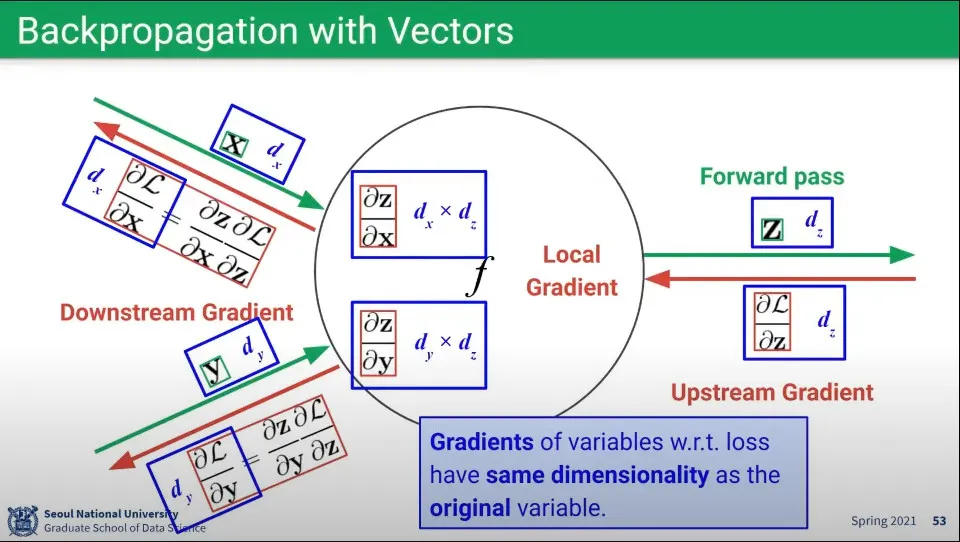
벡터에 대해 연산하면 위와 같다.
◦
이때 벡터끼리 곱해지는 Local Gradient는 Matrix가 만들어지게 되는데, Upstream Gradient와 Downstream Gradient과 곱하기를 하면 차원이 상쇄되어서 다시 벡터 형태로 만들어진다.
•
Vector에 대한 Foward, Backward 예
◦
함수가 max 였으므로, backward에서도 max 함수가 적용되어서 미분이 된다.
•
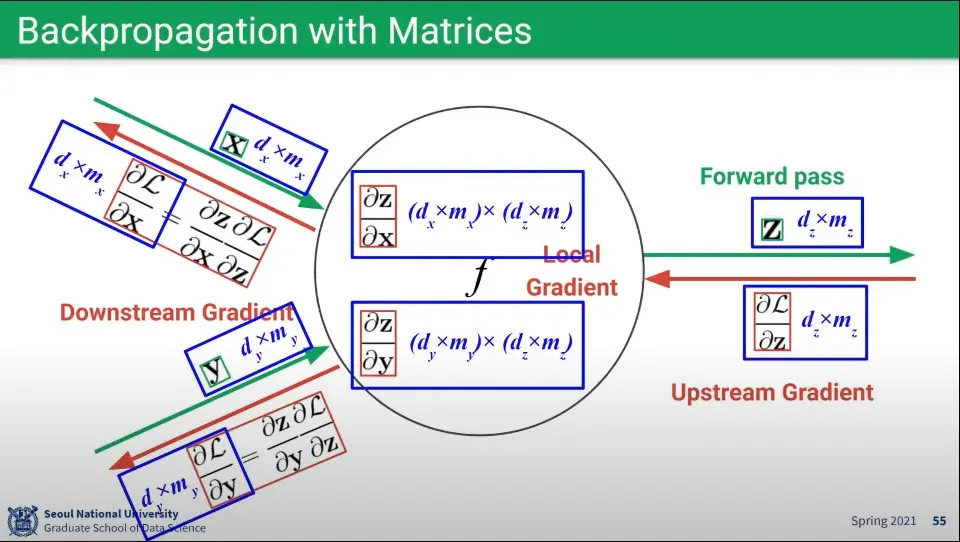
Matrix에 대한 예
◦
Local Gradient에서는 Matrix의 Matrix가 만들어지게 되는데, Vector 때와 마찬가지로 Upstream Gradient, Downstream Gradient와 곱해지면 차원이 상돼되어 다시 원래 크기의 Matrix가 만들어진다.