Abstract
우리는 object detection을 direct set prediction 문제로 보는 새로운 방법을 제안한다. 우리의 접근은 detection pipeline을 간소화하고, non-maximum suppression 절차나 anchor generation 같은 작업에 관한 prior 지식을 명시적으로 인코딩하는 많은 수작업 설계 컴포넌트의 필요성을 효과적으로 제거한다. DEtection TRansformat(DETR)이라 부르는 새로운 프레임워크의 주요 요소는 bipartite 매칭을 통해 고유한 예측을 강제하는 set-based global loss와 transformer encoder-decoder 아키텍쳐이다. DETR은 고정된 소수의 학습된 object query를 사용하여 object 간의 관계와 global 이미지 컨텍스트를 추론하고 최종 집합을 병렬로 직접 출력한다. 이 새로운 모델은 개념적으로 간단하고 다른 많은 현대 detector와 달리 특화된 라이브러리를 필요로 하지 않는다. DETR은 도전적인 COCO object detection 데이터셋에서 잘 확립되고 고도로 최적화된 Faster R-CNN baseline과 동등한 정확도와 실행시간 성능을 시연한다. 게다가 DETR은 통합된 방식으로 panotic segementation을 생성하도록 쉽게 일반화할 수 있다. 우리는 이것이 경쟁력 있는 baseline을 크게 능가하는 것을 보인다. 학습 코드와 pretrained 모델은 git에서 사용가능하다.
1 Introduction
object detection의 목표는 관심 있는 각 객체에 대한 bounding box와 category 라벨의 집합을 예측하는 것이다. 현대 detector는 이 집합 예측 작업을 간접적인 방법으로 다루는데, 대량의 proposals, anchors, windows centers에 대한 surrogate regression과 classification 문제를 정의하여 접근한다. 그들의 성능은 중복된 예측을 통합하는 post processing 단계, 앵커 집합의 설계, 그리고 타겟 박스를 앵커에 할당하는 휴리스틱에 의해 크게 영향을 받는다. 이러한 파이프라인을 단순화하기 위해 우리는 surrogate 작업을 우회하는 direct set prediction 접근을 제안한다. 이 end-to-end 철학은 기계 번역이나 음성 인식 같은 복잡한 구조화된 예측 작업에서 큰 진보를 이끌었지만 object detection에서는 그렇지 못했다. 이전 시도들은 다른 형식의 prior 지식을 추가하거나 도전적인 벤치마크에서 강력한 baseline과 경쟁력 있는 결과를 보여주지 못했다. 이 논문은 이러한 간격을 해소하는데 초점을 맞춘다.
우리는 object detection을 direct set prediction 문제로 봄으로써 학습 파이프라인을 간략화 한다. 우리는 시퀀스 예측에 대중적인 아키텍쳐인 transformer에 기반한 encoder-decoder 아키텍쳐를 채택한다. transformer의 self-attention 메커니즘은 시퀀스 내의 모든 요소 간의 상호작용을 명시적으로 모델링하므로, 중복 예측 제거와 같은 집합 예측의 특정 제약 조건에 특히 적합하다.
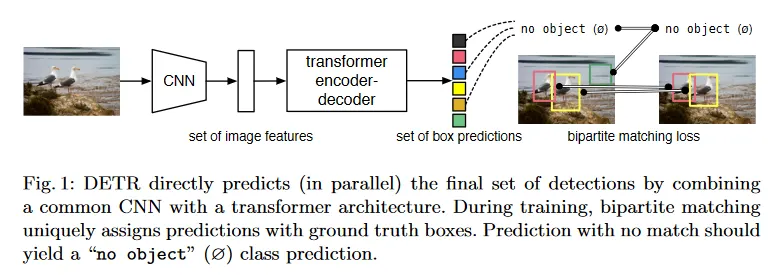
우리의 DEtection TRansformer(DETR, 그림 1)은 모든 object를 한 번에 예측하고, 예측과 ground-truth object 사이의 bipartite 매칭을 수행하는 set loss 함수를 사용하여 end-to-end로 학습된다. DETR은 공간적 anchor 또는 non-maximal suppression 같은 prior 지식을 인코딩하는 여러 수작업 설계 컴포넌트를 제거하여 detection 파이프라인을 단순화한다. 대부분 기존 detection 방법과 달리 DETR은 임의의 커스터마이징 레이어를 필요로 하지 않으므로 표준 CNN과 transformer 클래스를 포함하는 임의의 프레임워크에 쉽게 재현될 수 있다.
direct set prediction에 대한 대부분 이전 작업과 비교하여, DETR의 주요 feature는 bipartite 매칭 loss와 (non-autoregressive)parallel decoding을 사용하는 transformer의 결합이다. 반면 이전 작업은 RNN을 사용하는 autoregressive decoding에 초점을 맞춘다. 우리의 매칭 손실 함수는 각 예측을 ground truth object에 고유하게 할당하고 이것은 예측된 object의 permutation(순열)에 불변이다. 따라서 그것들을 병렬로 출력할 수 있다.
우리는 COCO라는 가장 대중적인 object detection 데이터셋 중 하나에서 DETR을 평가하고, 매우 경쟁력 있는 Faster R-CNN baseline과 비교한다. Faster R-CNN은 많은 설계 반복을 거쳤고 원래의 배포 이후 그 성능이 매우 개선 되었다. 우리의 실험은 우리의 새로운 모델이 경쟁력 있는 성능을 달성함을 보인다. 더 정확하게 DETR은 대형 object에 대해 매우 뛰어난 성능을 시연하는데, 이는 transformer의 non-local 계산에 의해 가능한 결과이다. 그러나 작은 object에 대해서는 낮은 성능을 보인다. 우리는 미래의 작업이 FPN이 Faster R-CNN에 대해 그랬던 것처럼 이 측면을 개선할 것으로 기대한다.
DETR을 위한 학습 설정은 표준 object detector와 여러 방법에서 차이가 있다. 새로운 모델은 매우 긴 학습 스케쥴을 필요로 하며 transformer에서 보조적인 decoding 손실의 이점을 얻는다. 우리는 어떤 컴포넌트가 입증된 성능에 결정적인지 철저히 탐구한다.
DETR의 설계 ethos(철학)는 더 복잡한 작업으로 쉽게 확장된다. 우리의 실험에서, pre-trained DETR 위에 학습된 간단한 segmentation head가 최근 인기를 얻고 있는 도전적인 픽셀-레벨 인식 작업인 Panoptic Segmentation에서 경쟁력 있는 baseline을 능가함을 보인다.
2 Related work
우리의 작업은 여러 도메인의 prior 작업 위에 구축한다. set 예측에 대한 bipartite matching loss, transformer에 기반한 encoder-decoder 아키텍쳐, parallel decoding와 object detection 방법들.
2.1 Set Prediction
set을 직접 예측하는 표준 deep learning 모델은 없다. 기본적인 set 예측 작업은 multi-label classification이다. 이에 대한 baseline 접근인 one-vs-rest는 element 사이에 기본 구조가 있는 detection 같은 문제(예: 거의 동일한 박스)에는 적용되지 않는다. 이러한 작업의 첫 번째 어려움은 중복에 가까운 것을 피하는 것이다. 대부분 현재 detector는 이 이슈를 해결하기 위해 non-maximal suppression 같은 후처리 작업을 사용하지만 direct set prediction은 후처리가 필요 없다. 그들은 중복을 제거하기 위해 모든 예측된 요소 사이의 상호작용을 모델링하는 전역 추론 스키마가 필요하다. 고정 크기 set prediction의 경우, dense fully connected 네트워크는 충분하지만 비용이 많이 든다. 일반적인 접근은 RNN 같은 auto-regressive 시퀀스 모델을 사용하는 것이다. 모든 경우에 loss 함수는 예측의 순열에 불변이어야 한다. 일반적인 솔루션은 Hungarian 알고리즘에 기반한 loss를 설계하여 ground-truth와 예측 사이의 biparite 매칭을 찾는 것이다. 이것은 순열-불변성을 강제하고 각 타겟 요소가 고유한 매칭을 보장한다. 우리는 bipartite 매칭 loss 접근을 따른다. 반면 대부분의 prior 작업과 달리, 우리는 autoregressive 모델에서 벗어나 parallel decoding을 사용하는 transformer를 사용한다. 아래 설명.
2.2 Transformers and Parallel Decoding
Transformer는 기계 번역을 위한 새로운 attention 기반 빌딩 블록으로 Vaswani et al에 의해 도입되었다. Attention 메커니즘은 전체 입력 시퀀스에서 정보를 aggregate(집계)하는 신경망 레이어이다. self-attention layer를 도입한 Transformer는 Non-Local 신경망과 유사하게, 시퀀스의 각 엘레먼트를 스캔하고 전체 시퀀스에서 정보를 aggregate하여 업데이트한다. attention 기반 모델의 주요 장점은 전역 계산과 perfect 메모리로, 이는 더 긴 시퀀스에서 RNN 보다 더 적합하게 만든다. Transformer는 이제 자연어 처리, 음성 처리, computer vision의 많은 문제에서 RNN을 대체했다.
Transformer는 초기 seq-to-seq 모델을 따라 auto-regressive 모델에서 처음 사용되어 출력 토큰을 하나씩 생성한다. 그러나 prohibitive(높은) 추론 비용(출력 길이에 비례하고 batch 처리가 어려움)으로 인해 오디오, 기계 번역, 단어 표현 학습과 더 최근 음성 인식의 도메인에서 병렬 시퀀스 생성의 발전을 이끌었다. 우리는 또한 transformer와 병렬 decoding을 결합하여 계산 비용과 set 예측을 위해 필요한 전역 계산 능력 사이의 trade-off를 적합하게 한다.
2.3 Object detection
대부분의 현대 object detection 방법은 어떤 초기 추측에 예측을 relative(상대적)으로 한다. Two-stage detector는 proposals에 대해 box 예측하는 반면, single-stage 방법은 앵커나 가능한 object 중심의 grid에 관한 예측을 한다. 최근 작업은 이러한 시스템의 최종 성능이 이러한 초기 추측을 설정하는 정확한 방법에 매우 의존함을 보였다. 우리의 모델에서 이러한 수작업 절차를 제거하고, 앵커에 대해 상대적으로 예측하는 대신, 입력 이미지에 대해 absolute(절대적) 박스 예측으로 detection의 집합을 직접 예측하여 detection 절차를 간략화할 수 있다.
Set-based loss.
여러 object detector는 bipartite matching loss를 사용한다. 그러나 이러한 초기 딥러닝 모델에서 서로 다른 예측 사이의 관계가 오직 convolutional 또는 fully-connected layer만으로 모델링되었고, 수작업으로 설계된 NMS 후처리가 그들의 성능을 개선할 수 있었다. 더 최근 detector는 NMS와 함께 ground truth와 예측 사이의 비고유한 할당 규칙을 사용한다.
학습가능한 NMS 방법과 relation network는 attention을 사용하여 서로 다른 예측 사이의 관계를 명시적으로 모델링한다. direct set loss를 사용하여 임의의 후처리 단계를 요구하지 않는다. 그러나 이런 방법들은 detection 사이의 관계를 효율적으로 모델링하기 위한 proposal box 좌표와 같은 추가적인 수작업 context feature를 활용한다. 반면 우리는 모델에 인코딩된 prior 지식을 줄이는 솔루션을 찾는다.
Recurrent detectors.
우리의 접근과 가장 가까운 것은 object detection과 instance segmentation을 위한 end-to-end set 예측이다. 우리와 유사하게 그들은 CNN 활성화에 기반한 encoder-decoder 아키텍쳐와 함께 bipartite-matching loss를 사용하여 bounding-box의 집합을 직접 생성한다. 그러나 이러한 접근은 작은 데이터셋에서만 평가되었고, 현대의 baseline에 대항하지 못한다. 특히 그들은 auto-regressive model(더 정확하게 RNN)에 기반으로 하므로 parallel decoding을 사용하는 최근 transformer를 활용하지 못한다.
3 The DETR model
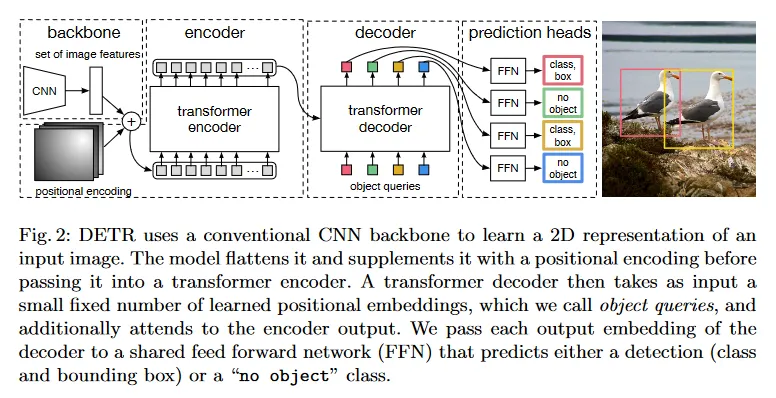
detection에서 direct set prediction을 위해 2가지 재료가 필수적이다. (1) 예측과 ground truth box 사이의 고유한 매칭을 강제하는 set prediction loss (2) object의 집합을 (single pass) 예측하고 그들의 관계를 모델링하는 아키텍쳐. 우리의 아키텍쳐의 상세를 그림 2에 그린다.
3.1 Object detection set prediction loss
DETF은 decoder를 단일 경로로 통과하여 고정된 크기의 개 예측을 추론한다. 여기서 은 이미지에서 객체의 일반적인 숫자보다 매우 커질 수 있다. 학습의 주요 어려움 중 하나는 예측된 object(class, position, size)를 ground truth와 비교하여 점수를 매기는 것이다. 우리의 loss는 예측과 ground truth object 사이의 최적의 bipartite 매칭을 생성한 다음 object별 (bounding box) loss를 최적화 한다.
를 object의 ground truth 집합이라 하고 을 개 예측의 집합이라 표기하자. 이 이미지의 object의 수보다 더 커질 수 있다고 가정하여, 우리는 또한 (no object)로 패딩된 크기 의 집합으로 고려한다. 이러한 두 집합 사이의 bipartite 매칭을 찾기 위해, 가장 낮은 비용을 갖는 개 elements의 순열 을 탐색한다.
여기서 는 ground truth 와 index 의 예측 사이의 pair-wise matching cost이다. 이 최적 할당은 prior 연구를 따라 Hungarian 알고리즘을 사용하여 효율적으로 계산될 수 있다.
matching 비용은 class 예측과 예측된 박스와 ground truth 박스의 유사도를 모두 고려한다. ground truth 집합의 각 번째 element는 로 볼 수 있다. 여기서 는 타겟 클래스 라벨(일 수 있는)이고 는 ground truth box의 중심 좌표와 이미지 크기에 대한 relative(상대적) height와 width를 정의하는 벡터이다. index 의 예측을 위해 우리는 클래스 의 확률을 로 예측된 박스를 로 정의한다. 이러한 표기를 사용하여 우리는 를 로 정의한다.
이 매칭 찾기 절차는 현대 detector에서 proposal이나 앵커를 ground truth object에 매칭하는데 사용되는 휴리스틱 할당 규칙과 같은 역할을 한다. 주요 차이는 중복 없는 direct set prediction을 위해 일대일 매칭을 찾아야 한다는 것이다.
두 번째 단계는 이 loss 함수를 계산하는 것이다. 이전 단계에서 매칭된 모든 쌍에 대한 Hungarian loss를 계산한다. 우리는 일반적인 object detector의 loss와 유사하게 loss를 정의한다. 즉 클래스 예측을 위해 negative log-likelihood와 이후에 정의할 box loss의 선형 결합이다.
여기서 는 첫 번째 단계 (1)에서 계산된 최적 할당이다. 실제로 우리는 클래스 불균형을 고려하여 일 때 log 확률 항의 가중치를 의 factor로 낮춘다. 이것은 R-CNN 학습 절차가 subsampling을 통해 positive/negative proposal의 균형을 잡는 방식과 유사하다. object 와 사이의 매칭 비용이 예측에 의존하지 않는다는 것에 유의하라. 이것은 그 경우 비용이 상수인 경우를 의미한다. 매칭 비용에서 우리는 log 확률 대신 확률 를 사용한다. 이것은 클래스 예측 항을 (아래에 설명할)와 측정 가능하게 만들고, 실험적으로 더 나은 성능을 관찰했다.
Bounding box loss
매칭 비용과 Hungarian loss의 두 번째 부분은 bounding box에 점수를 매기는 이다. 어떤 초기 추정에 관한 로 box 예측을 수행하는 많은 detector와 달리, 우리는 box 예측을 직접 한다. 이런 접근은 구현을 단순화하지만, loss의 relative scaling 이슈를 제기한다. 대부분 일반적으로 사용되는 loss는 상대적 에러가 유사할지라도 작은 박스와 큰 박스에 대해 서로 다른 스케일을 갖는다. 이 이슈를 완화하기 위해 우리는 loss와 스케일 불변인 일반화된 IoU loss 의 선형결합을 사용한다. 전체적으로 우리의 box loss는 로 정의되는 이다. 여기서 은 하이퍼파라미터이다. 이 두 loss는 batch 내부의 object의 수에 의해 normalize 된다.
3.2 DETR architecture
전체적인 DETR 아키텍쳐는 놀라울 정도로 간단하고 그림 2에 묘사된다. 이것은 아래 설명할 3가지 주요 컴포넌트를 포함한다. compact feature representation을 추출하는 CNN backbone, encoder-decoder transformer와 최종 detection 예측을 수행하는 간단한 feed-forward network(FFN).
다른 현대 detector와 달리 DETR은 일반적인 CNN backbone과 transformer 아키텍쳐를 제공하는 임의의 딥러닝 프레임워크에서 몇 백 줄의 코드로 구현될 수 있다. DETR을 위한 추론 코드는 PyTorch에서 50줄도 안 되게 구현할 수 있다. 우리는 우리의 방법의 단순성이 새로운 연구자들을 detection 커뮤니티로 이끌기를 희망한다.
Backbone
초기 이미지 (3채널) 에서 시작하고, convolutional CNN backbone은 더 낮은 해상도 활성화 맵 를 생성한다. 우리가 사용하는 일반적인 값은 이고 이다.
Transformer encode
우선 1x1 convolution은 high-level 활성화 맵 의 채널 차원을 에서 더 작은 차원 로 축소하여 새로운 feature map 를 생성한다. 인코더는 입력으로 시퀀스를 기대하므로 우리는 의 공간 차원을 1차원으로 축소하여 feature map을 만든다. 각 인코더 레이어는 표준 아키텍쳐를 가지며, multi-head self-attention 모듈과 feed forward network(FFN)으로 구성된다. transformer 아키텍쳐가 순열 불변이기 때문에 우리는 각 attention layer의 입력에 추가되는 fixed positional encoding을 보충한다. 아키텍쳐의 상세한 정의는 [47]의 설명을 따르며, 보충 자료에서 더 자세히 다룬다.
Transformer decoder
디코더는 transformer의 표준 아키텍쳐를 따르며 multi-headed self-attention과 encoder-decoder attention 메커니즘을 사용하여 크기 의 embedding을 transforming한다. 원래의 transformer와의 차이는 우리의 모델이 각 디코더 레이어에서 개 object를 병렬로 디코딩하는 반면 Vaswani et al은 출력 시퀀스를 한 번에 하나씩 예측하는 autoregressive model을 사용한다는 것이다. 이 개념에 익숙하지 않은 독자는 보충 자료 참조. 디코더가 또한 순열 불변이기 때문에 개 입력 임베딩은 서로 다른 결과를 생성해야 하기 위해 서로 달라야 한다. 이러한 입력 임베딩은 우리가 object query라 부르는 학습된 positional encoding이며, 우리는 그것들을 각 attention 레이어의 입력에 추가한다. 개 object query는 디코더에 의해 출력 임베딩으로 transformed 된다. 그 다음 그들은 feed forward network(다음 하위 섹션에서 설명되는)에 의해 독립적으로 box 좌표와 클래스 라벨로 디코딩 되어 개 최종 예측을 생성한다. 이러한 embedding에 대해 self-attention과 encoder-decoder attention을 사용함으로써 모델은 전체 이미지를 맥락으로 사용하면서 object 간의 pair-wise 관계를 사용하여 모든 object에 대해 전역적으로 추론한다.
Prediction feed-forward networks (FFNs)
최종 예측은 ReLU 활성화 함수와 은닉 차원 를 갖는 3개 레이어 퍼셉트론과 선형 projection 레이어에 의해 계산된다. FFN은 입력 이미지에 관한 box의 normalized 중심 좌표, height와 width를 예측하고 linear 레이어는 softmax 함수를 사용하여 클래스 라벨을 예측한다. 우리는 고정된 크기의 개 bounding box의 집합을 예측하는데, 여기서 은 일반적으로 이미지 내의 관심 있는 object의 실제 수보다 훨씬 커질 수 있기 때문에, slot 내에 검출된 object가 없음을 나타내는 추가적인 특별 클래스 라벨 을 사용한다. 이 클래스는 표준 object detection 접근에서 ‘backbround’ 클래스와 유사한 역할을 수행한다.
Auxiliary decoding losses
우리는 학습하는 동안 디코더에 auxiliary loss를 사용하는게 도움이 된다는 것을 발견했다. 특히 모델이 각 클래스의 올바른 object 수를 출력하는데 도움이 된다. 우리는 각 디코더 레이어 이후에 예측 FFN과 Hungarian loss를 추가한다. 모든 예측 FFN은 파라미터를 공유한다. 우리는 서로 다른 디코더 레이어에서 예측 FFN으로의 입력을 normalize하기 위해 추가적으로 공유된 layer-norm을 사용한다.
4 Experiments
(생략)
5 Conclusion
우리는 transformer와 direct set prediction을 위한 bipartite 매칭 loss에 기반한 object detection 시스템에 대한 새로운 설계인 DETF을 제안했다. 이 접근은 challenging COCO 데이터셋에서 최적화된 Faster R-CNN baseline에 비교할만한 결과를 달성했다. DETR은 구현이 간단하고 유연한 아키텍쳐를 갖고 있어 panotic segmentation으로 쉽게 확장가능하며 경쟁력 있는 결과를 보인다. 게다가 이것은 selft-attention에 의해 수행된 global 정보의 처리 덕분에 Faster R-CNN 보다 큰 object에 대해 더 나은 성능을 달성했다.
이 새로운 detector 설계는 또한 새로운 도전, 특히 학습, 최적화와 작은 object에 대한 성능 측면에서 과제들 동반한다. 현재 detector들은 유사한 문제를 해결하기 위해 수년의 개선이 필요했으며, 우리는 향후 연구가 DETF을 위해 성공적으로 그것을 해결할 것이라 기대한다.
A Appendix
A.1 Preliminaries: Multi-head attention layers
(생략)
A.2 Losses
완전성을 위해 우리의 접근에서 사용된 loss를 자세히 제시한다. 모든 loss는 batch 내의 object의 수로 normalize 된다. 분산 학습에 대해서는 특별한 주의가 필요하다. 각 GPU가 sub-batch를 받기 때문에 local batch에서 object의 수로 normalize 하는 것은 충분하지 않다. 일반적으로 sub-batch는 GPU간에 균형을 이루지 않는다. 대신 모든 sub-batch의 총 object 수로 normalize 하는 것이 중요하다.
Box loss
[41, 36]과 유사하게 우리는 우리의 loss에서 Intersection over Union의 soft 버전을 사용하며, 이와 함께 에 대한 을 loss를 사용한다.
여기서 은 하이퍼파라미터이고 은 일반화된 IoU이다.
은 ‘area’를 의미하고 box 좌표의 합집합과 교집합은 box 자체를 나타내는 축약으로 사용된다. 합집합이나 교집합의 area는 와 의 선형 함수의 로 계산되며, 이는 loss가 stochastic gradient를 위해 충분히 잘 작동하게 만든다. 는 를 포함하는 가장 큰 box를 의미한다(와 관련된 area도 box 좌표의 선형 함수의 를 기반으로 계산된다.)
DICE/F-1 loss
DICE 계수는 Intersection over Union과 밀접하게 관련되어 있다. 만일 를 모델의 raw mask logit 예측으로, 을 binary target mask으로 표기하면, loss는 다음과 같이 정의된다.
여기서 는 sigmoid 함수이다. 이 loss는 object의 수에 의해 normalize 된다.
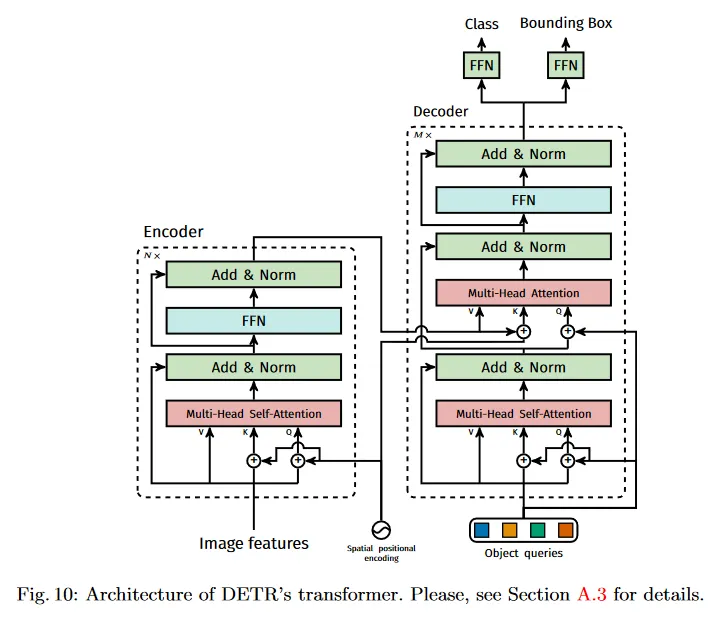
A.3 Detailed architecture
(이하 생략)