Lipschitz Constant
매끈한 함수에 대해 Lipschitz 상수를 사용하여 매끈함의 정도를 정량화할 수 있다. 이것은 함수의 입력의 변화 대한 출력의 변화를 나타내는 값으로, 모든 값 에 대해 다음을 만족하는 상수 로 정의 된다. (이것은 함수에 의해 결정되는 값으로 사용자가 정의할 수 있는 값은 아님)
이 1보다 작으면 출력의 변동은 입력의 변동보다 작다는 의미가 되게 되고, 이 1보다 크면 출력의 변동은 입력의 변동보다 크다는 의미가 된다. 즉 이 작을수록 함수는 더 천천히 변하고, 이는 함수가 매끄럽다는 것을 나타낸다. 반면 이 클수록 함수는 더 급격하게 변하고, 이는 함수가 덜 매끄럽다는 것을 나타낸다.
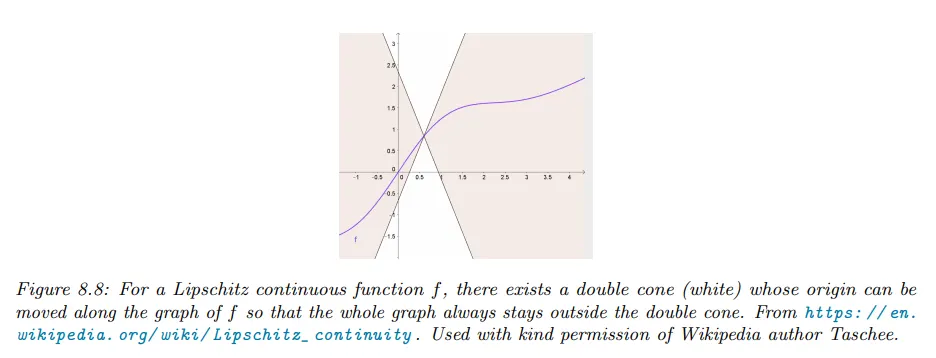
아래 그림 참조. 주어진 상수 에 대해 함수 입력을 1 단위 변경하면, 출력은 보다 크게 변경할 수 없다.
위 식을 변형하면 미분과의 연계성을 고려할 수 있다.
참고로 복소수 공간에서도 Lipschitz 조건은 동일하게 정의된다.
만일 복소수 공간이었다면 은 복소수 상수의 절대값이 되고, 복소수 벡터 공간인 경우 은 복소수 행렬의 노름이 된다.