•
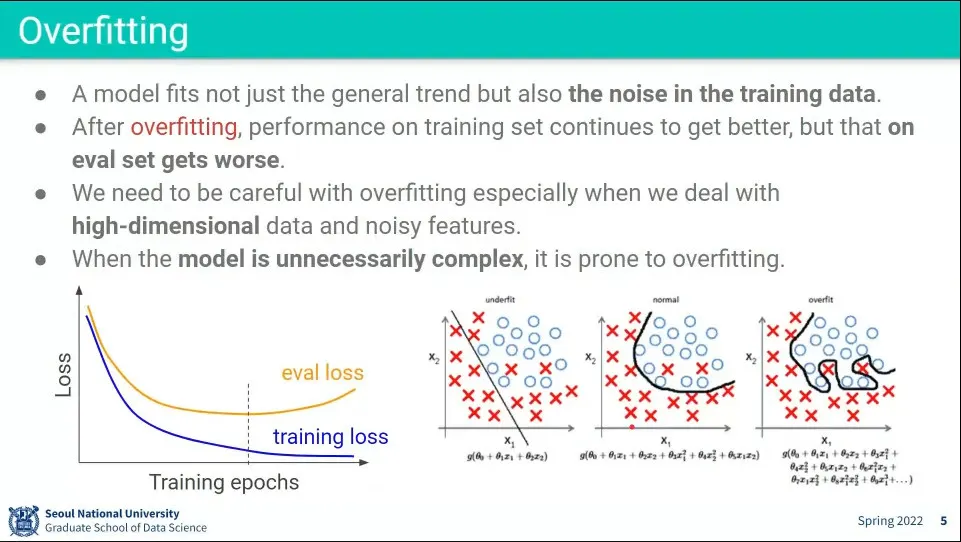
Overfitting(과적합)
◦
학습이 진행되면서 학습 데이터에 대해서는 loss가 떨어지고 있지만, 검증 데이터에 대해서는 오히려 loss가 올라가는 상태
•
과적합 문제를 방지하기 위해 Regularization(규제)을 사용함. 이것은 overfitting을 방지한다.
◦
Regularization은 일종의 페널티를 부여한다.
◦
예컨대 회귀 문제는 를 최소화하는 것을 찾게 되는데, 여기에 의 합을 더해줘서 (절대값을 더할 수도 있고(이게 L1) 제곱해서 더할 수도 있다(이게 L2)) (추가로 를 곱한) 무작정 를 최소화하는 것을 못 찾게 한다.
◦
머신러닝에서는 가중치 를 구하게 되는데, 이 를 강제로 더해줘서 규제를 사용함
•
기본적으로 복잡한 선을 그리려면 함수가 복잡해져야 한다.
◦
위 overfitting 이미지에서 가장 오른쪽의 복잡한 선을 그리려면 그 식 안에 속한 의 값이 커야 함. 만일 가 0에 가까운 작은 값이라면 복잡한 선을 그릴 수 없고, underfitting과 같은 단순한 선이 그려짐.
◦
그래서 단순한 모델을 만드는 것과 weight 값을 작게 만드는 것은 강한 상관관계가 있다.
◦
이래서 머신러닝에서 학습을 반복하면 가 점점 커지게 되는데, (식은 최소화된 를 잡게 되므로 그 안에서 작은 값을 찾게 되지만) 이거를 방지하기 위해 아예 를 더해줘서 균형을 잡는다.
•
L2 Regularization을 Ridge Regression이라고 한다.
◦
제곱의 합이기 때문에 원형으로 나타나고, 가 커질수록 원은 작아지고 작아질수록 원은 커짐.
◦
식의 값이 원을 벗어나지 못하기 때문에 만일 최적값이 원 밖에 존재하는 경우 그 최적값에 가장 가까운 원 위의 점이 최적값으로 잡힌다.
•
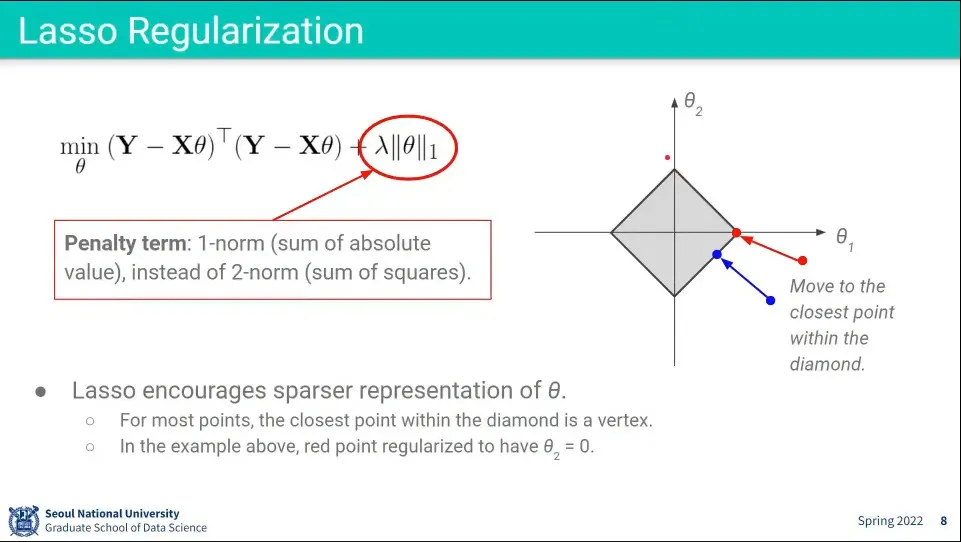
L1 Regularization을 Lasso Regularization이라고 한다.
◦
L2와 달리 절대값의 합이기 때문에 마름모 모양으로 표현된다.
◦
아까와 마찬가지로 가 커질수록 마름모는 작아지고 작아질수록 커짐.
◦
이 경우 많은 경우 최적값이 꼭지점에 모이게 되는데, 마름모 바깥의 많은 점들의 가장 가까운 거리가 꼭지점에 대응되기 때문. 변에 대응되는 영역은 좁은 영역만 가능하다.
◦
많은 점들이 꼭지점에 모인다는 것은 가 0이 된다는 것이 되고, 그것은 위의 복잡한 수식에서 많은 선들이 사라져서 결국 단순해 진다는 것이 된다.
◦
따라서 noise에 robust한 decision boundary를 만들게 된다.
•
neural network는 표현력이 뛰어나다는 특성 덕분에 overfitting이 매우 잘 일어난다. 때문에 이것을 방지하기 위해 아래와 같은 다양한 regularization 방법을 사용할 수 있다.
◦
Weight Decay
◦
Early Stopping
◦
Dropout
◦
DropConnect
•
선형회귀에서 Regularization을 했던게 Weight Decay이다.
◦
L1, L2 처럼 절대값을 더하거나 제곱을 더하거나 할 수 있음
•
Multi layer에도 마찬가지로 적용 가능
•
Early Stopping이란 validation set을 따로 만들어두고, overfitting이 발생하기 시작할 때 학습을 중지하는 것
◦
training loss는 떨어지고 있지만, evaluation loss가 떨어지다가 다시 증가하기 시작하는 시점
•
validation set을 train set에서 분리하면 그만큼 train set 줄어드니 성능이 떨어질 수 있다
•
test set은 학습 과정 중에 절대 사용되면 안된다.
◦
validation set은 보통 epoch 돌 때마다 함
•
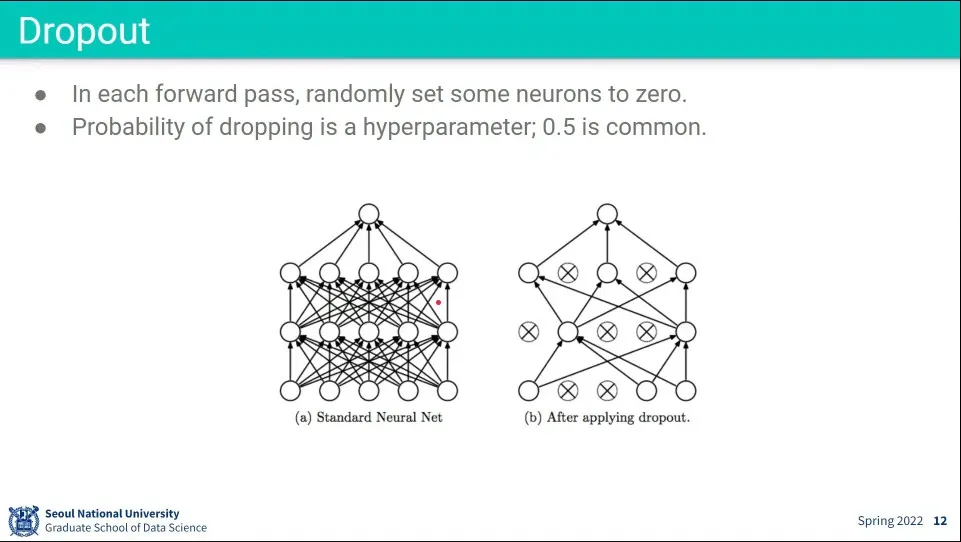
Dropout은 학습할 때 network 내의 임의의 node 들을 끄고 학습 시키는 것
•
dropout을 하지 않으면 대상의 한, 두 가지 특징에 overfitting 될 수 있다. 그래서 강제로 노드를 꺼서 최대한 다양한 특징을 학습 할 수 있도록 함
◦
일반화가 더 잘 될 수 있게 하는 것.
•
dropout 코드 구현 예
◦
학습할 때 랜덤으로 뽑고 p 값보다 낮은 애들은 0으로 만든다.
◦
그런데 단순히 끄면 scale이 변경되기 때문에 p 값으로 나누어서 조정해 줘야 한다.
•
실제 pytorch 등에서는 dropout을 별도의 layer로 만들고 통과시켜주는 방식으로 사용하게 됨
•
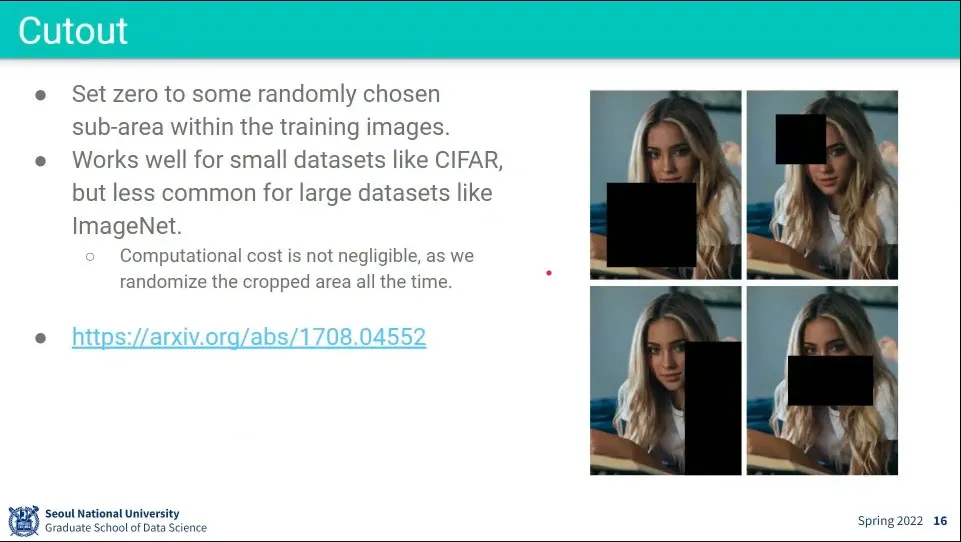
Cutout은 마치 Dropout처럼 데이터의 일부분을 제외하고 학습 시킴
•
fully-connected layer를 쓸 때는 dropout을 쓰는게 좋다.
•
batch normalization은 쓰는게 좋다
•
data augmentation은 쓰는게 좋다. 데이터셋이 작으면 특히 효과적이다.
•
early stopping은 final metric을 이용해서 어디서 멈춰야 하는지 결정해야 한다.
•
Stochastic Gradient Descent의 문제점
◦
느리다
◦
미분이 안되는 점을 만나면 더 못내려감
◦
mini-batch 기반으로 학습하는데 mini-batch의 estimation이 정확하지 않음
•
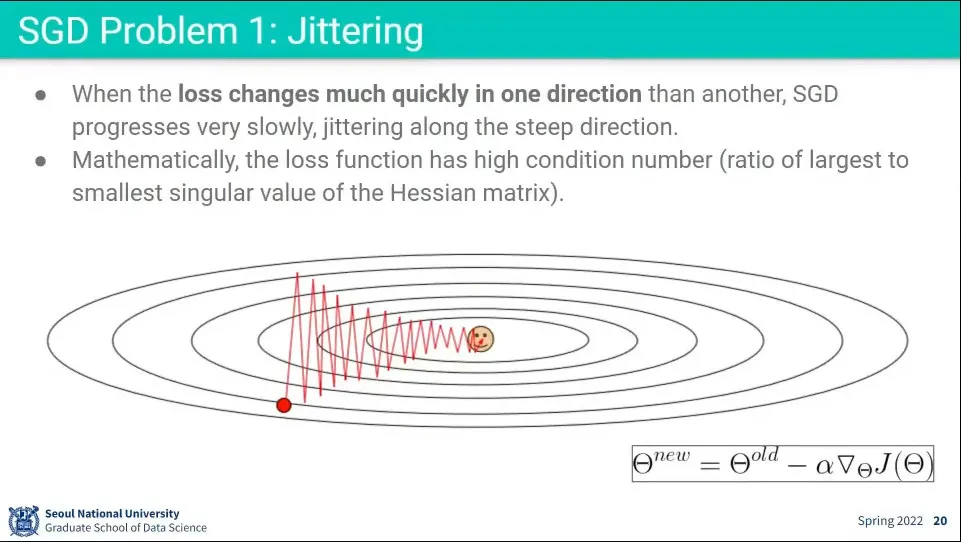
SGD는 느린데, Jittering 때문에 더 느려진다.
◦
만일 한 방향은 가파르고 다른 한 방향은 완만하다면 가파른 방향으로는 빠르게 움직이고 완만한 방향으로는 천천히 움직이는 jittering이 발생함. (왔다갔다)
◦
가팔랐던 방향은 조금씩 움직이고 완만했던 방향은 많이 움직이는게 더 좋은데 그 반대로 움직이고 있는 것
•
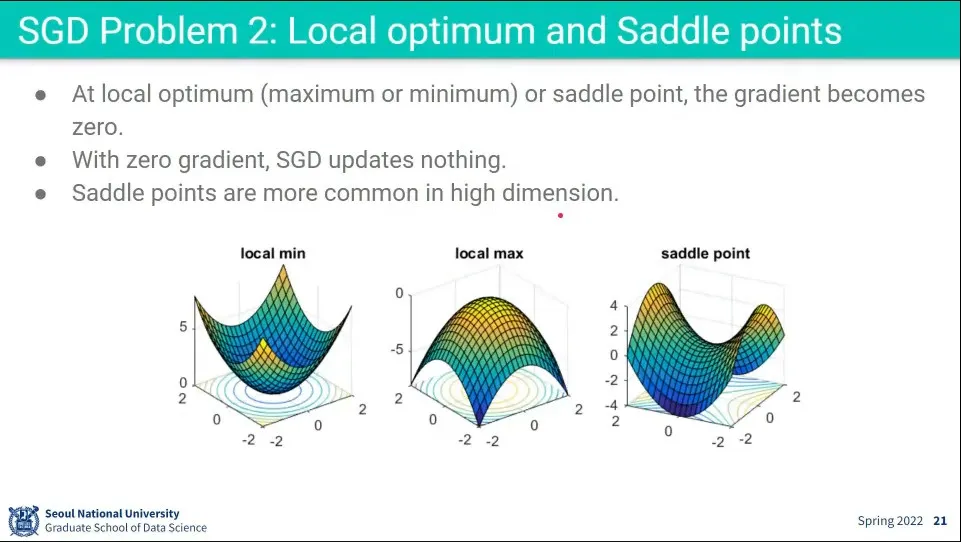
Saddle point 같은 지점에서 미분 값이 0이 나오기 때문에 더 내려가지 못 함
•
데이터셋이 큰 경우 mini-batch 사이즈가 그것을 따라가지 못하면 전체 데이터셋을 대변하지 못함.
◦
mini-batch는 메모리 한계로 한 번에 넣을 수 있는 크기의 한계가 있어서 4096도 엄청 큰 사이즈인데, 만일 전체 데이터셋이 10억개였다면 0.0004%의 데이터만 대변하게 됨
◦
따라서 현재 계산 중인 Gradient가 전체에 대해서도 옳은지 확신할 수 없음
•
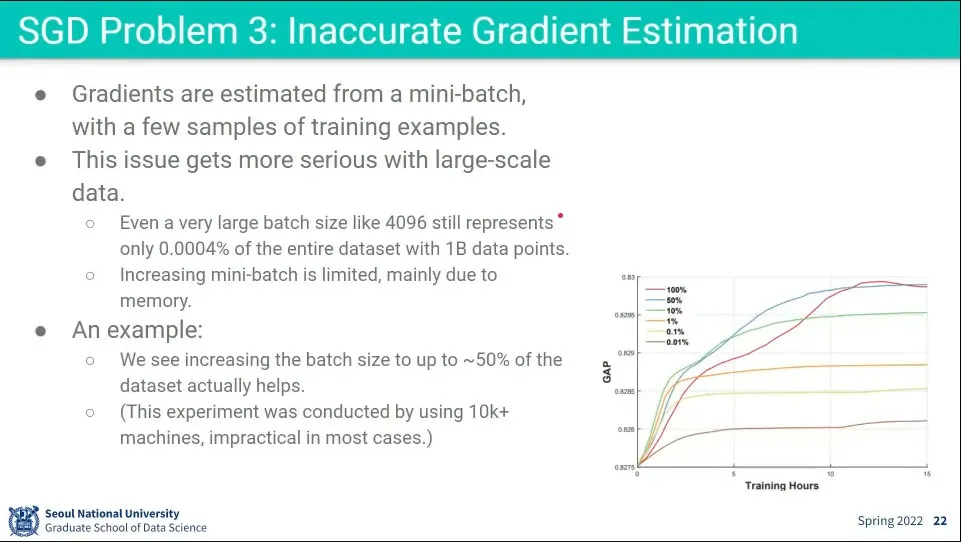
오른쪽 아래 그래프를 보면 batch-size가 전체 데이터셋을 많이 커버할 수록 성능이 점점 좋아짐
◦
그래프상으로는 batch size가 전체 데이터셋에 대해 50%까지는 성능이 계속 좋아짐. 그 이상은 큰 변화 없음
•
SGD에 쓰이는 Momentum은 본래 물리학에서 쓰이는 것과는 다름
◦
물리학에서 inertia(관성)는 어떤 물체가 운동을 유지하려는 성질의 정도이고 momentum은 어떤 물체가 얼마나 빠르게 운동하는지를 정량적으로 나타내는 정도를 말함. 이때 momentum은 mass와 velocity의 곱으로 표현 됨.
◦
여기서 말하는 말하는 Momemtum은 사실 관성(inertia)에 가까움
•
전 단계의 velocity에 상수()를 곱해서 현재 gradient에 더해 줌
◦
이 과정이 일종의 history처럼 작용해서 한 방향으로 이동하고 있었으면 그 방향으로 힘을 더 해줌
◦
이러면 지그재그를 덜하고 더 빠르게 움직일 수 있음
◦
이렇게 하면 saddle point를 통과할 수 있음. 미분은 0이지만 관성이 있었기 때문에 움직일 수 있음
•
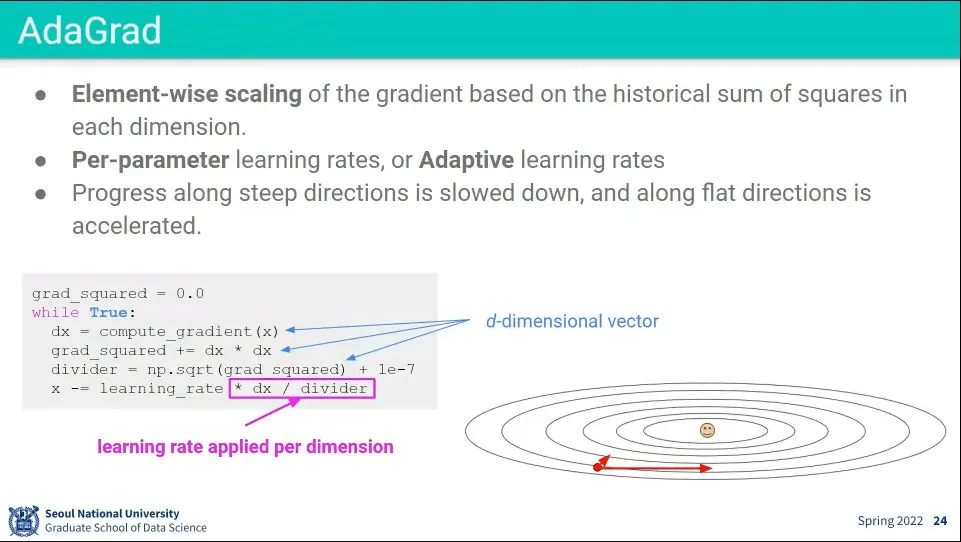
AdaGrad는 학습할 때 Dimension마다 Learning rate를 별개로 주는 방식
◦
Ada는 Adaptive의 약자
◦
Element-wise로 scaling을 해준다.
•
어느 Dimension에 얼마의 Learning rate이 적절한지를 알 수 없기 때문에 학습하면서 계산함.
◦
divider는 Dimension 별로 이전 Gradient의 제곱을 누적하는 것인데,
◦
이것이 분모로 들어가기 때문에 이전에 Gradient가 가팔랐던 애들은 조금만 움직이게 하고, Gradient가 완만했던 애들은 많이 움직일 수 있게 해 줌
•
그런데 AdaGrad는 과거를 양수(제곱했으므로)로 누적하기 때문에 분모가 커지기만 함.
◦
이래서 시간이 지날수록 분모가 커져서 업데이트가 점점 느려짐
◦
이것을 보완하기 위해 과거 데이터를 decay 시켜 주는게 Leaky AdaGrad. RMSprop이라고도 한다.
•
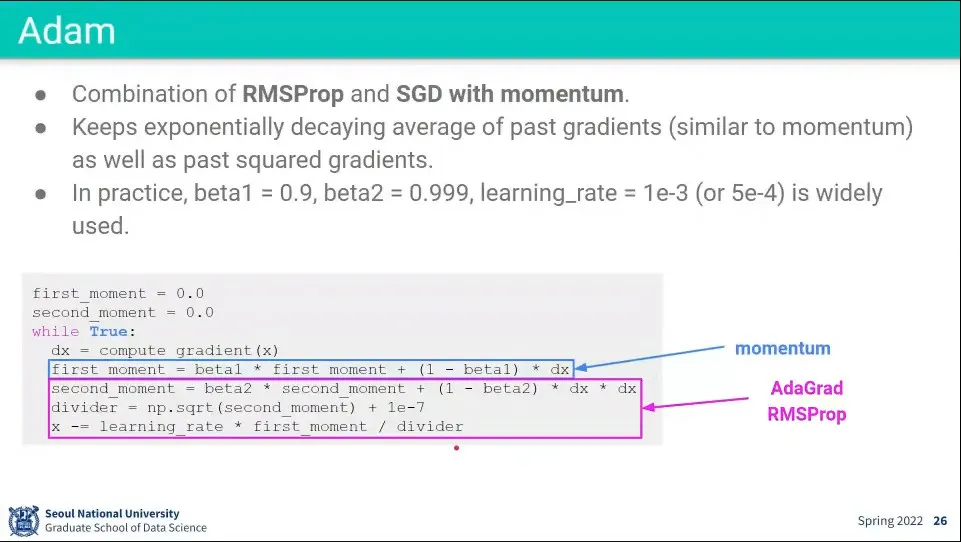
Adam은 Ada + momentum으로 앞선 Momentum과 RMSProp을 모두 사용하는 방법이다.
◦
가장 발전된 방법이기 때문에 일단 시작할 때는 Adam으로 시작함
•
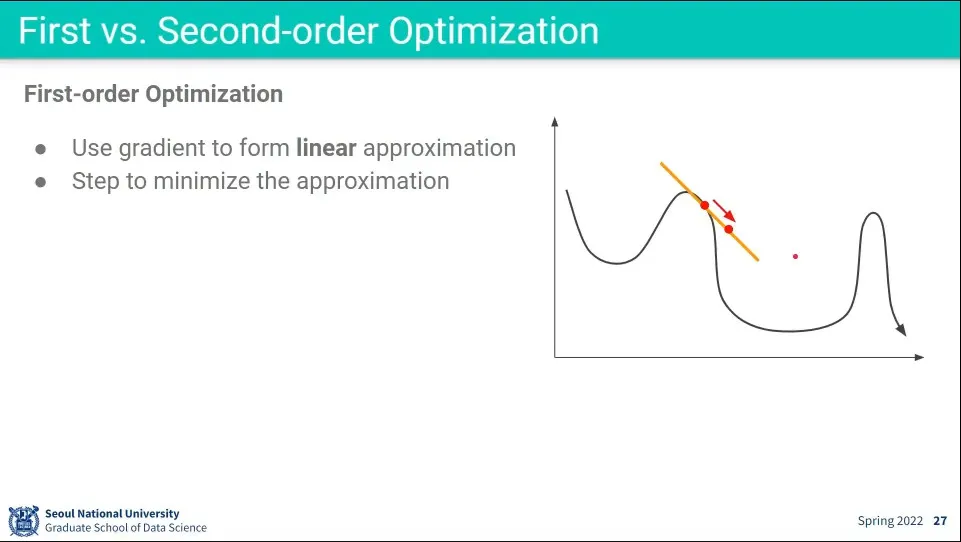
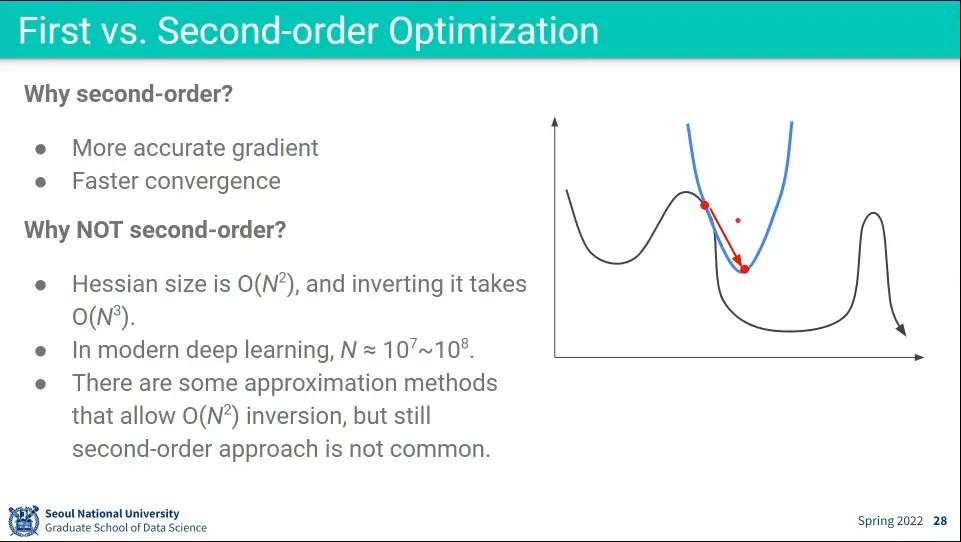
1차 최적화은 현재 위치에서 Gradient를 선형(1차 함수)으로 구해서 감소하는 방향으로 움직이게 하는 것
•
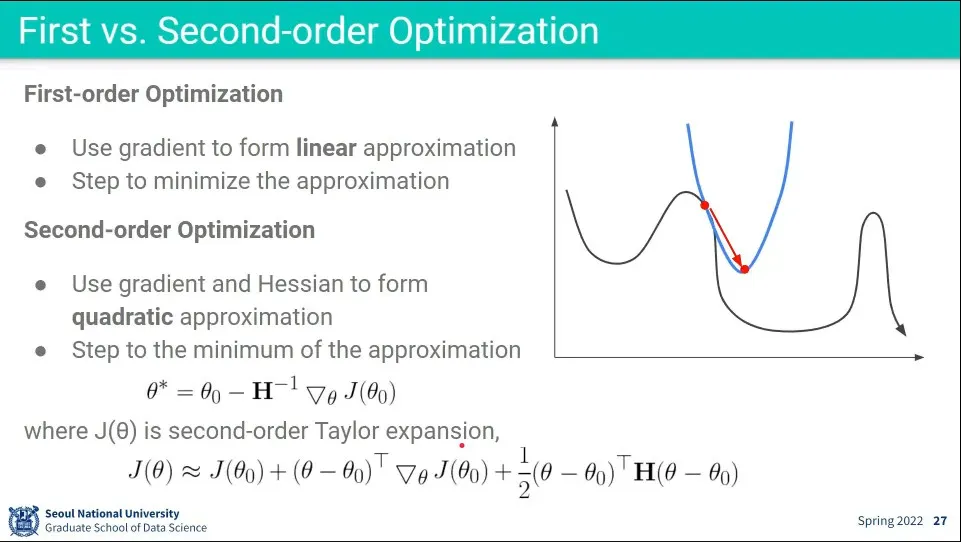
2차 최적화는 2차 함수 형태로 구해서 Gradient를 구하는 것
◦
2차 함수를 그대로 사용하기 어려우니 테일러 전개를 이용해서 2차식을 근사함
◦
그런데 이 식에서 사용되는 가 행렬인데, 그것을 구하기 위해 역행렬을 구해야 함. 그게 시간이 엄청 걸림
◦
최적점을 더 빠르게 찾을 수 있지만, 역행렬 구하는 계산이 1차식 푸는 것보다 더 오래 걸림
•
2차 최적화을 사용하면 더 정확하고 수렴을 빨리 할 수 있지만, 연산 속도가 느리다.
◦
역행렬을 구하는 속도가 에 비례하기 때문. 현대의 딥러닝에서 사용하는 의 크기가 에 이르기 때문에 더더욱 오래 걸린다.
•
그래서 2차 최적화를 실용적으로 사용하지는 않는다.
•
최적화를 할 때는 일단 Adam으로 시작해서 돌려보고 최적화를 위해 다른 것을 시도해 볼 수 있다.
•
초기 learning rate가 중요하기 때문에 적절하게 조절해야 함.
•
머신러닝 모델을 구성하고 적절한 파라미터를 찾는데는 경험이 요구됨
•
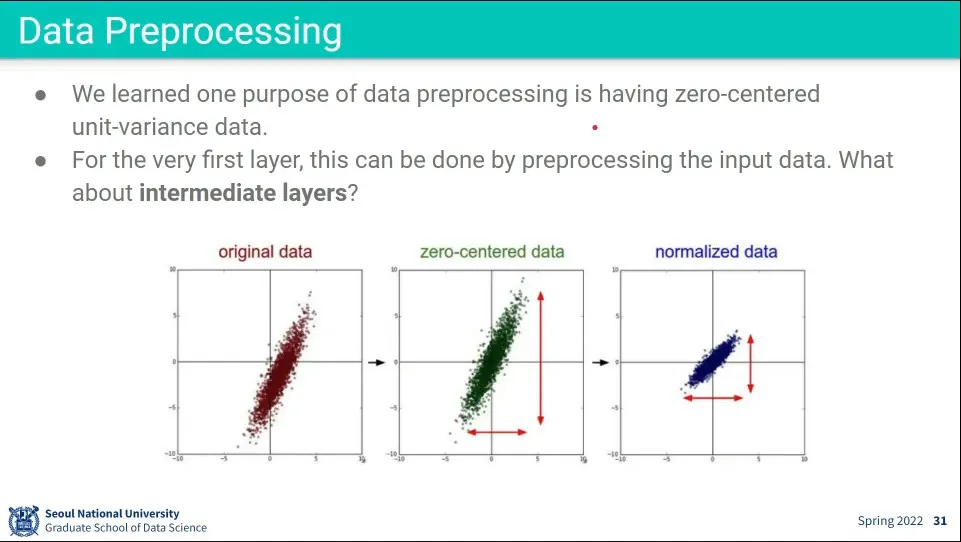
데이터 전처리 과정에서 zero-centered하고 normalized 시켜주는게 좋다.
•
근데 이것은 가장 앞의 layer에만 적용되고, neural network가 깊어지면 뒤의 layer에는 이게 전달이 잘 안 됨
•
이 문제를 해결하기 위해 해당 layer에서 normalizationd을 직접 시켜주는 방법이 있음
◦
input에 대해 평균을 빼고 표준편차로 나눈다.
•
데이터를 normalizatoin 할 평균과 표준편차는 미니배치에서 계산한다.
•
무작정 normalization 하면 값이 깨지기 때문에, 그것을 다시 원복할 수 있는 계산을 해줘야 함.
◦
위 식에서 는 normalization한 것이고
◦
이것을 다시 원복 시키기 위해 와 를 구해줘야 하는데 —이때 는 표준편차의 역할을 해줘야하고 는 평균(기댓값) 역할을 해줘야 함— 는 따로 구하지 않고 학습을 통해 배우도록 함.
◦
그러면 적당히 비슷한 값이 나오게 된다.
•
고로 batch normalization 할 때는 앞에 normalization 하는 것과 함께 뒤에 원복하는 것도 넣어줘야 한다.
•
테스트할 때는 평균과 표준편차를 구할 수 없기 때문에 학습할 때 값을 저장해 두었다가 사용해야 함.
•
Batch Normalization은 계산량은 복잡하지 않은데, 그 효과는 크기 때문에 표준처럼 사용 된다.
•
batch normalization은 학습과 테스트의 평균과 표준편차가 유사하다는 가정하에 만들어진 것인데, 하지만 현실의 데이터는 계속 변하기 때문에 모델이 학습된지 시간이 오래 지나면 그것을 보장할 수 없음
◦
또한 만일 학습 데이터 자체가 큰 경우 mini batch 크기가 작아질 수 밖에 없는데 —메모리 크기의 한계로— 그런 경우 그 mini batch에서의 평균과 분산이 전체 데이터를 얼마나 잘 반영할 수 있느냐는 확신할 수 없음.
•
그래서 원래의 논문 저자들이 그것을 반영하라고 batch renormalization을 새로 발표함
•
PyTorch에 Batch Normalization Layer을 추가할 때는 Activation Layer 전에 넣으면 된다. input 데이터를 normalization 해주는 개념이기 때문
◦
코드에 1d라고 나오는 것은 2d, 3d도 있다는 뜻
•
Batch Normalization 이후에 다양한 Normalization 방법이 나옴.
◦
이 중에 Layer Normalization은 실제로 많이 사용 됨