Search
Duplicate

AI/ Structure From Motion(SFM), Bundle Adjustment

Structure From Motion(SFM)

Structure From Motion(SFM)은 다수의 2d 이미지를 이용하여 카메라의 파라미터와 3d 구조를 재구성하는 기술을 의미한다.
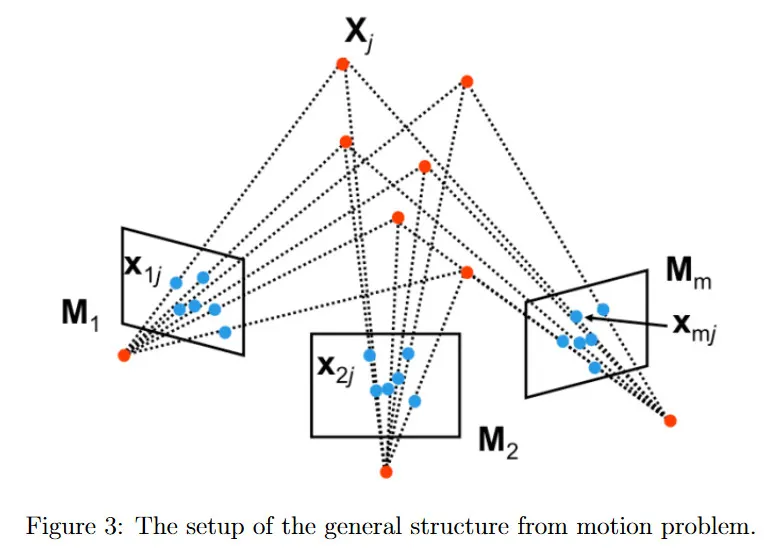
아래의 내용을 설명하기 위해 위의 그림에 따라 mm개의 MiM_i는 카메라에 대한 intrinsic과 extrinsic 파라미터를 모두 인코딩하는 카메라 변환이고, nn개의 XjX_j는 3d 포인트이고, xijx_{ij}는 XjX_j를 MiM_i을 사용하여 카메라 ii의 이미지에 projection한 것이다.
SFM의 목표는 모든 관찰 xijx_{ij}에서 장면의 structure(nn개 3d 점 XjX_j)와 카메라의 motion(mm개 projection 행렬 MiM_i)를 복구하는 것이다.

Affine SFM

SFM에 대해 카메라가 affine 또는 weak perspective라는 가정에서 시작한다. full perspective 모델에 대해 카메라 행렬이 다음과 같이 정의 된다.
M=[Abv1]M = \begin{bmatrix} A & b \\ v & 1 \end{bmatrix}
여기서 vv는 non-zero 1×31 \times 3 벡터이다. weak perspective model의 경우 v=0v = 0이다. 이 속성은 MXMX의 homogeneous 좌표를 1로 만든다.
x=MX=[m1m20001][X1X2X31]=[m1Xm2X1]x = MX = \begin{bmatrix} m_1 \\ m_2 \\ 0 \quad 0 \quad 0 \quad 1 \end{bmatrix} \begin{bmatrix} X_1 \\ X_2 \\ X_3 \\ 1 \end{bmatrix} = \begin{bmatrix} m_1X \\ m_2X \\ 1 \end{bmatrix}
결과적으로 homogeneous에서 유클리드 좌표로 이동하면서 projective transformation의 비선형성은 사라지고 weak perspective transformation은 확대기 역할을 한다. 위의 projection을 다음과 같이 더 간결하게 나타낼 수 있다.
[m1Xm2X]=[Ab]X=AX+b\begin{bmatrix} m_1X \\ m_2X \end{bmatrix} = \begin{bmatrix} A & b \end{bmatrix}X = AX + b
모든 카메라 행렬을 Maffine=[Ab]M_\text{affine} = [A \quad b] 형식으로 나타낼 수 있다. 따라서 affine 카메라 모델을 사용하여 3d 점 XjX_j과 각 affine 카메라에서의 해당하는 관측치간의 관계(예컨대 카메라 ii에서 xijx_{ij})를 표현할 수 있다.
SFM 문제에서 mnmn개 관찰에서 mm개의 행렬 MiM_i에 대해 3개의 intrinsic와 5개의 extrinsic를 고려하여 8m8m의 파라미터와 nn개 월드 좌표 벡터 XjX_j에 대해 3개의 좌표 x,y,zx, y, z를 고려하여 3n3n의 파라미터를 합한 총 8m+3n8m + 3n개의 미지수를 추정해야 한다. 각 관측치는 카메라당 2개의 제약을 생성하므로 8m+3n8m + 3n개의 미지수에 대해 2mn2mn 방정식이 존재한다.
8m+3n=2mn8m + 3n = 2mn
이 방정식을 사용하여 각 이미지에서 대응점이 필요한 최소 개수의 하한을 알 수 있다. 예컨대 m=2m=2개의 카메라를 가지면, 3d에서 최소 n=16n=16개의 점이 필요하다.
affine SFM을 해결하기 위해 data centering step과 actual factorization step으로 구성되는 Tomasi and Kanade factorization 방법을 사용할 수 있다. 이에 대한 상세한 내용은 Computer Vision/ 4. Stereo Systems의 3.2 부분 참조.

Perspective SFM

Affine SFM에 대한 일반적인 경우가 Perspective SFM이다. projective 카메라의 일반적인 경우 각 카메라 행렬 MiM_i는 scale까지 정의되어 11개의 자유도를 포함한다.
Mi=[a11a12a13b1a21a22a23b2a31a32a331]M_i = \begin{bmatrix} a_{11} & a_{12} & a_{13} & b_1 \\ a_{21} & a_{22} & a_{23} & b_2 \\ a_{31} & a_{32} & a_{33} & 1 \end{bmatrix}
affine 경우에 해가 affine transformation까지만 결정되는 것처럼 일반적인 경우에 structure와 motion에 대한 해는 projective transformation까지만 결정될 수 있다.
Perspective SFM에서는 카메라 모델이 더 일반적이기 때문에 5개의 intrinsic과 6개의 extrinsic을 고려하여 8m8m의 파라미터와 3개의 좌표 x,y,zx, y, z를 고려하여 3n3n의 파라미터를 합한 다음 scale 변환을 고려하여 전체 시스템에서 15개의 불필요한 자유도를 뺀 총 11m+3n−1511m + 3n - 15개의 미지수를 추정해야 한다. 따라서 미지수 개수에 대해 다음 등식을 갖는다.
11m+3n−15=2mn11m + 3n - 15 = 2mn
Perspective SFM에서는 Fundamental Matrix FF를 활용한다. 이 방법의 주요 아이디어는 perspective transformation HH까지만 계산할 수 있는 카메라 행렬 MiM_i을 계산한다. 이에 대한 상세한 내용은 Computer Vision/ 4. Stereo Systems의 4.1 부분 참조.

Bundle Adjustment

SFM 문제는 모든 점이 모든 이미지에서 visible이라는 가정을 하기 때문에 한계가 있다. 이것은 이미지 상에 occlusion으로 하나의 카메라에서만 보이는 영역이 존재하는 경우나 이미지가 멀리 떨어져있는 경우 등으로 인해 현실적이지 않은 가정이다.
Bundle Adjustment는 SFM의 한계를 해결하는 비선형 방법으로 이것은 재구성된 점을 추정된 카메라로 projection할 때와 모든 카메라와 모든 점에 대한 대응 관측치 사이의 픽셀 거리인 reprojection error를 최소화하는데 초점을 맞춘다.
bundle adjustment는 여러 카메라를 다루며 카메라가 볼 수 있는 관찰에 대해서만 reprojection error를 계산한다. 그렇지만 궁극적으로 이 최적화 방법은 triangulation에 대한 비선형 방법과 매우 유사하다.
bundle adjustment의 비선형 최적화를 해결하는 일반적인 두 가지 접근은 Gauss-Newton algorithm과 Levenberg-Marquardt algorithm이다. 두 알고리즘의 상세 내용은 생략.
bundle adjustment는 많은 수의 view를 smooth하게 다룰 수 있고, 특정한 점이 모든 이미지에서 관찰되지 않은 경우도 다룰 수 있다는 점에서 유용하지만, view가 증가함에 따라 파라미터가 증가하므로 큰 최소화 문제라는 단점이 존재한다. 또한 비선형 최적화 기법에 의존하므로 좋은 초기화가 필요하다.
이러한 이유로 bundle adjustment는 SFM 구현의 마지막 단계에 사용되는 경우가 많다. SFM의 factorization과 Algebraic 접근이 최적화 문제에 대한 좋은 초기 해를 제공하기 때문이다.

참고

Made with