Search
Duplicate

수학/ Multivariate Student, Circular Normal, Matrix Normal, Wishart, Inverse Wishart, Dirichlet 분포

Multivariate Student distribution

•
Student 분포를 DD차원으로 쉽게 확장할 수 있다. 특히 다변량 student 분포의 pdf는 다음과 같이 주어진다.
Tν(x∣μ,Σ)=1Z[1+1ν(x−μ)⊤Σ−1(x−μ)]−(ν+D2)Z=Γ(ν/2)Γ(ν/2+D/2)νD/2πD/2∣Σ∣−1/2\begin{aligned} \mathcal{T}_\nu(\bold{x}|\boldsymbol{\mu},\boldsymbol{\Sigma}) &= {1 \over Z} \left[1 + {1 \over \nu}(\bold{x} - \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1}(\bold{x}-\boldsymbol{\mu}) \right]^{-({\nu + D \over 2})} \\ Z &= {\Gamma(\nu/2) \over \Gamma(\nu/2 + D/2)}{\nu^{D/2}\pi^{D/2} \over |\boldsymbol{\Sigma}|^{-1/2}} \end{aligned}
•
여기서 Σ\boldsymbol{\Sigma}는 scale 행렬이라 부른다.
•
student는 가우시안 보다 두꺼운 꼬리를 갖는다. ν\nu가 작을수록 꼬리가 더 두꺼워진다. ν→∞\nu \to \infty이면 분포는 가우시안에 가까워지는 경향이 있다. 이 분포는 다음의 속성을 갖는다.
mean=μ,mode=μ,cov=νν−2Σ\text{mean} = \boldsymbol{\mu}, \text{mode} = \boldsymbol{\mu}, \text{cov} = {\nu \over \nu-2} \boldsymbol{\Sigma}
•
평균은 (유한) ν>1\nu > 1일 때만 잘 정의된다. 유사하게 공분산은 ν>2\nu > 2일 때만 잘 정의된다.

Circular normal (von Mises Fisher) distribution

•
때때로 데이터가 유클리드 공간의 임의의 점이 아니라 단위 원에 존재할 수 있다. 예컨대 ℓ2\ell_2-normalized DD-차원 벡터는 RD\mathbb{R}^D의 (D−1)(D-1) 단위 구에 임베딩 되어 있다.
•
von Mises-Fisher 분포 또는 circular normal 분포라고 부르는 가우시안 분포의 확장은 이런 angular 데이터에 대해 적합하다. 다음의 pdf를 갖는다.
vMF(x∣μ,κ)≜1Zexp⁡(κμ⊤x)Z=(2π)D/2ID/2−1(κ)κD/2−1\begin{aligned} \text{vMF}(\bold{x}|\boldsymbol{\mu},\kappa) &\triangleq{1\over Z} \exp(\kappa \boldsymbol{\mu}^\top\bold{x}) \\ Z &= {(2\pi)^{D/2} I_{D/2-1}(\kappa) \over \kappa^{D/2-1}} \end{aligned}
•
여기서 μ\boldsymbol{\mu}는 평균 (∥μ∥=1\|\boldsymbol{\mu}\| = 1인)이고,
◦
κ≥0\kappa \ge 0은 농도(concentration) 또는 정밀도(precision) 파라미터(표준 가우시안의 1/σ1/\sigma와 유사)이고
◦
ZZ는 정규화 상수이다.
◦
Ir(⋅)I_r(\cdot)는 첫 번째 종류의 수정된 Bessel 함수이고 차수 rr이다.
◦
vMF는 유클리드 거리 대신 cosine 거리로 파라미터화된 구형 다변량 가우시안과 같다.
•
가우시안 혼합 모델을 사용하는 대신 혼합 모델 내부에서 ℓ2\ell_2-normalized 벡터를 클러스터링 하기 위해 vMF 분포를 사용할 수 있다. κ→0\kappa \to 0이면 구형 K-mean 알고리즘으로 축소된다.
◦
이 알고리즘은 혼합(admixture) 모델의 내부에서도 사용될 수 있다. 이것을 spherical topic model이라 부른다.
•
D=2D=2인 경우 대안은 다음 형식을 갖는 단위 원에서 von Mises 분포를 사용하는 것이다.
vMF(x∣μ,κ)=1Zexp⁡(κcos⁡(x−μ))Z=2πI0(κ)\begin{aligned} \text{vMF}(x|\mu,\kappa) &= {1 \over Z} \exp(\kappa \cos(x - \mu)) \\ Z &= 2 \pi I_0(\kappa) \end{aligned}

Matrix normal distribution (MN)

•
matrix normal 분포는 다음과 같이 행렬 X∈Rn×p\bold{X} \in \mathbb{R}^{n \times p}에 대한 확률 밀도 함수로 정의된다.
MN(X,M,U,V)≜∣V∣n/22πnp/2∣U∣p/2exp⁡{−12tr[(X−M)⊤U−1(X−M)V)]}\mathcal{MN}(\bold{X}, \bold{M},\bold{U},\bold{V}) \triangleq {|\bold{V}|^{n/2} \over 2\pi^{np/2}|\bold{U}|^{p/2}}\exp \left\{ -{1 \over 2} \text{tr}[(\bold{X}-\bold{M})^\top \bold{U}^{-1}(\bold{X}-\bold{M})\bold{V})] \right\}
•
여기서 M∈Rn×p\bold{M} \in \mathbb{R}^{n \times p}는 X\bold{X}의 평균값이고 U∈S++n×n\bold{U} \in \mathcal{S}_{++}^{n \times n}는 행 사이의 공분산이고, V∈S++p×p\bold{V} \in \mathcal{S}_{++}^{p \times p}는 열 사이의 정밀도 이다. 이것은 다음처럼 볼 수 있다.
vec(X)∼N(vec(M),V−1⊗U)\text{vec}(\bold{X}) \sim \mathcal{N}(\text{vec}(\bold{M}),\bold{V}^{-1} \otimes \bold{U})
•
V\bold{V} 대신에 column-covariance 행렬 V~=V−1\tilde{\bold{V}} = \bold{V}^{-1}을 사용하여 다음의 밀도를 이끄는 행렬 normal 분포의 정의를 하는 다른 버전이 있다.
12πnp/2∣U∣p/2∣V~∣n/2exp⁡{−12tr[(X−M)⊤U−1(X−M)V~−1]}{1\over 2\pi^{np/2}|\bold{U}|^{p/2}|\tilde{\bold{V}}|^{n/2}}\exp \left\{-{1\over2} \text{tr} \left[(\bold{X}-\bold{M})^\top \bold{U}^{-1}(\bold{X}-\bold{M})\tilde{\bold{V}}^{-1} \right] \right\}
•
이 두 가지 버전의 정의는 분명히 동등하다. 그러나 위의 방정식 MN(X,M,U,V)≜∣V∣n/22πnp/2∣U∣p/2exp⁡{−12tr[(X−M)⊤U−1(X−M)V)]}\mathcal{MN}(\bold{X}, \bold{M},\bold{U},\bold{V}) \triangleq {|\bold{V}|^{n/2} \over 2\pi^{np/2}|\bold{U}|^{p/2}}\exp \left\{ -{1 \over 2} \text{tr}[(\bold{X}-\bold{M})^\top \bold{U}^{-1}(\bold{X}-\bold{M})\bold{V})] \right\} 가 posterior의 정돈된 업데이트를 이끈다.
◦
켤례 prior의 다변량 정규 분포의 posterior를 해석에서 공분산 행렬 보다 정밀도 행렬을 사용하는 것이 더 편리한 것처럼.

Wishart distribution

•
Wishart 분포는 감마 분포를 양의 정부호 행렬로 일반화한 것이다. ‘Wishart 분포는 다변량 통계에서 중요함과 유용함의 측면에서 정규 분포 다음 순위이다.’라는 주장도 있다. 대부분 이것을 공분산 행렬을 추정할 때 불확실성을 모델링하기 위해 사용한다.
•
Wishart의 pdf는 다음과 같이 정의된다.
Wi(Σ∣S,ν)≜1Z∣Σ∣(ν−D−1)/2exp⁡(−12tr(S−1Σ))Z≜∣S∣−ν/22νD/2ΓD(ν/2)\begin{aligned} \text{Wi}(\boldsymbol{\Sigma}|\bold{S},\nu) &\triangleq {1 \over Z}|\boldsymbol{\Sigma}|^{(\nu-D-1)/2} \exp \left(-{1\over2} \text{tr}(\bold{S}^{-1}\boldsymbol{\Sigma}) \right) \\ Z &\triangleq |\bold{S}|^{-\nu/2}2^{\nu D/2} \Gamma_D(\nu/2) \end{aligned}
•
여기서 ν\nu는 자유도이고 S\bold{S}는 scale 행렬이다. 정규화 상수는 ν>D−1\nu > D-1일 때만 존재한다(따라서 pdf는 잘 정의된 경우에만 존재한다).
•
분포는 다음의 속성을 갖는다.
mean=νS,mode=(ν−D−1)S\text{mean} = \nu\bold{S}, \text{mode} = (\nu-D-1)\bold{S}
•
최빈값(mode)가 ν>D+1\nu > D + 1에만 존재함에 유의하라.
•
D=1D=1이면 위샤트는 감마 분포로 축소된다.
Wi(λ∣s−1,ν)=Ga(λ∣shape=ν2,rate=12s)\text{Wi}(\lambda|s^{-1},\nu) = \text{Ga}(\lambda|\text{shape} = {\nu \over 2}, \text{rate} = {1\over 2s})
•
s=2s=2이면 chi-squared 분포로 축소된다.
•
위샤트 분포와 가우시안 사이에 흥미로운 연결이 존재한다. 특히 xn∼N(0,Σ)\bold{x}_n \sim \mathcal{N}(0,\boldsymbol{\Sigma})에서 scatter 행렬 S=∑n=1Nxnxn⊤\bold{S} = \sum_{n=1}^N \bold{x}_n\bold{x}_n^\top이 위샤트 분포 S∼Wi(Σ,N)\bold{S} \sim \text{Wi}(\boldsymbol{\Sigma}, N)을 갖는 것을 보일 수 있다.

Inverse Wishart distribution

•
λ∼Ga(a,b)\lambda \sim \text{Ga}(a,b)이면 1λ∼IG(a,b){1 \over \lambda} \sim \text{IG}(a,b)인 것과 유사하게 Σ−1∼Wi(S−1,ν)\boldsymbol{\Sigma}^{-1} \sim \text{Wi}(\bold{S}^{-1},\nu)이면 Σ∼IW(S,ν)\boldsymbol{\Sigma} \sim \text{IW}(\bold{S},\nu)이다. 여기서 IW는 inverse Wishart이다. inverse gamma의 다차원 일반화이다.
•
ν>D−1\nu > D - 1과 S≻0\bold{S} \succ 0에 대해 다음과 같이 정의된다.
IW(Σ∣S−1,ν)=1Z∣Σ∣−(ν+D+1)/2exp⁡(−12tr(SΣ−1))ZIW=∣S∣ν/22νD/2ΓD(ν/2)\begin{aligned} \text{IW}(\boldsymbol{\Sigma}|\bold{S}^{-1},\nu) &= {1\over Z} |\boldsymbol{\Sigma}|^{-(\nu + D + 1) / 2} \exp \left(-{1\over 2} \text{tr}(\bold{S}\boldsymbol{\Sigma}^{-1}) \right) \\ Z_\text{IW} &= |\bold{S}|^{\nu/2}2^{\nu D/2}\Gamma_D(\nu/2) \end{aligned}
•
이 분포가 다음 속성을 갖는 것을 보일 수 있다.
mean=Sν−D−1,mode=Sν+D+1\text{mean} = {\bold{S} \over \nu - D - 1}, \text{mode} = {\bold{S} \over \nu + D + 1}
•
D=1D=1이면 inverse gamma로 축소된다.
IW(σ2∣s−1,ν)=IG(σ2∣ν/2,s/2)\text{IW}(\sigma^2|s^{-1},\nu) = \text{IG}(\sigma^2|\nu/2,s/2)
•
s=1s = 1이면 inverse chi-squared 분포로 축소된다.

Dirichlet distribution

•
베타 분포의 다변량 일반화는 Dirichlet 분포이다. 이것은 다음과 같이 정의되는 확률 simplex에 대한 support를 제공한다.
SK={x:0≤xk≤1,∑k=1Kxk=1}S_K = \{\bold{x} : 0 \le x_k \leq 1, \sum_{k=1}^K x_k = 1\}
•
pdf는 다음과 같이 정의된다.
Dir(x∣α)≜1B(α)∏k=1Kxkαk−1I(x∈SK)\text{Dir}(\bold{x}|\boldsymbol{\alpha}) \triangleq {1 \over B(\boldsymbol{\alpha})} \prod_{k=1}^K x_k^{\alpha_k - 1}\mathbb{I}(\bold{x} \in S_K)
•
여기서 B(α)B(\boldsymbol{\alpha})는 다변량 베타 함수이다.
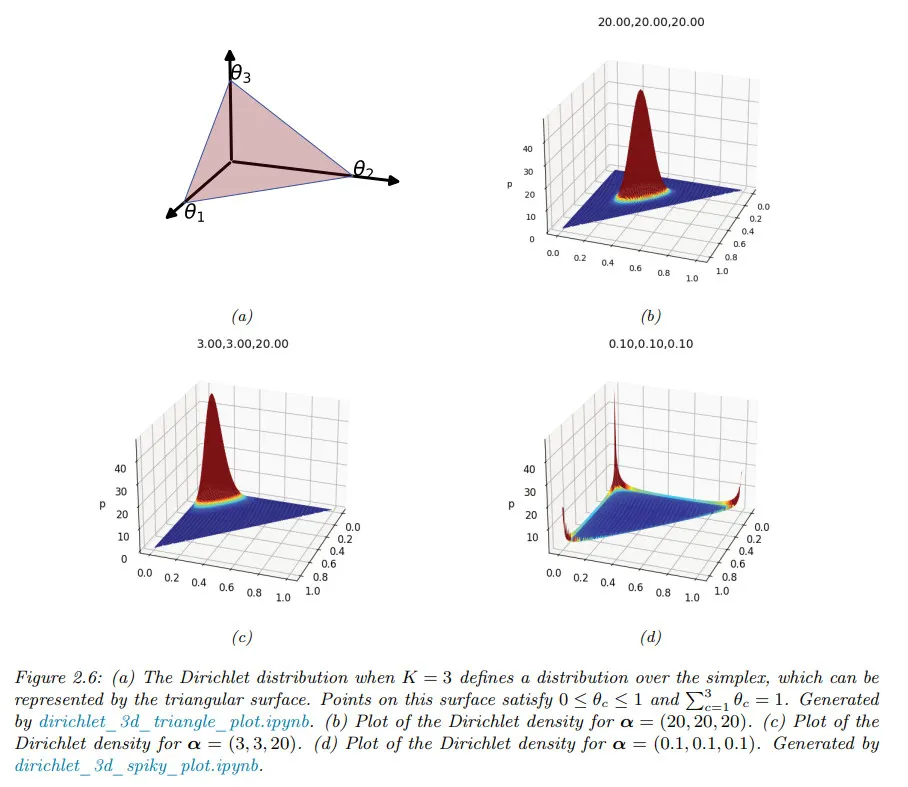
B(α)≜∏k=1KΓ(αk)Γ(∑k=1Kαk)B(\boldsymbol{\alpha}) \triangleq {\prod_{k=1}^K \Gamma(\alpha_k) \over \Gamma(\sum_{k=1}^K \alpha_k)}
•
아래 그림은 K=3K=3일 때 디리클레를 plot한 것이다.
◦
α0=∑kαk\alpha_0 = \sum_k \alpha_k는 분포의 강도(얼마나 peaked인지)를 제어하고, αk\alpha_k는 어디서 peak가 나타나는지를 제어하는지를 볼 수 있다.
◦
예컨대 Dir(1,1,1)\text{Dir}(1,1,1)은 균등 분포이고 Dir(2,2,2)\text{Dir}(2,2,2)는 (1/3,1/3,1/3)(1/3,1/3,1/3)에 중심을 둔 넓은(broad) 분포이다.
◦
Dir(20,20,20)\text{Dir}(20,20,20)은 (1/3,1/3,1/3)(1/3,1/3,1/3)에 중심을 둔 좁은(narrow) 분포이다.
◦
Dir(3,3,20)\text{Dir}(3,3,20)는 1개의 코너에 더 많은 밀도가 부여된 비대칭 분포이다.
•
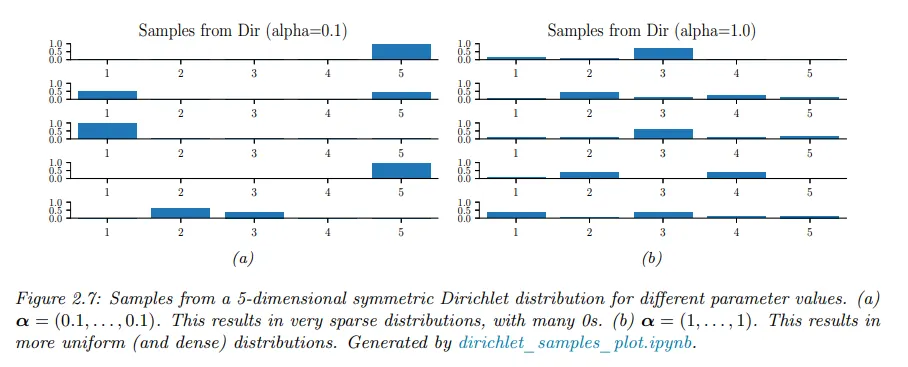
모든 kk에 대해 αk<1\alpha_k < 1이면 simplex의 코너에 spike를 갖는다. αk<1\alpha_k <1일 때 분포의 샘플은 희소하다. 아래 그림 참조.
•
디리클레 분포의 다음과 같은 유용한 속성이 있다. 여기서 α0=∑kαk\alpha_0 = \sum_k \alpha_k
E[xk]=αkα0,mode[xk]=αk−1α0−K,V[xk]=αk(α0−αk)α02(α0+1)\mathbb{E}[x_k] = {\alpha_k \over \alpha_0}, \text{mode}[x_k] = {\alpha_k-1 \over \alpha_0 - K}, \mathbb{V}[x_k] = {\alpha_k(\alpha_0 - \alpha_k) \over \alpha_0^2(\alpha_0+1)}
•
종종 αk=α/K\alpha_k = \alpha / K 형식의 대칭 디리클레 prior를 사용한다. 이 경우에 E[xk]=1/K\mathbb{E}[x_k] = 1/K와 V[xk]=K−1K2(α+1)\mathbb{V}[x_k] = {K-1 \over K^2(\alpha+1)}을 갖는다.
◦
따라서 α\alpha를 증가시킴에 따라 분포의 정밀도가 증가하는 것(분산은 감소)을 볼 수 있다.
•
디리클레 분포는 aleatoric (데이터) 불확실성과 인식적(epistemic) 불확실성을 구분하는데 유용하다.
◦
이를 알아보기 위해 3면 주사위를 생각해 보자. 각 결과가 똑같이 나올 확률이 높다는 것을 안다면 위 그림에 표시된 Dir(20,20,20)\text{Dir}(20,20,20)과 같은 ‘peak’ 대칭형 디리클레 분포를 사용할 수 있는데, 이는 결과를 예측할 수 없다는 사실을 반영한 것이다.
◦
반대로 결과가 어떻게 나올지 확실하지 않은 경우(예컨대 편향된 주사위일 수 있음), Dir(1,1,1)\text{Dir}(1,1,1)과 같은 ‘편평한’ 대칭형 디리클레를 사용하면 다양한 결과 분포를 생성할 수 있다.
◦
디리클레 분포를 입력에 따라 조건부로 만들 수 있는데 이는 p(y∣x)p(y|\bold{x})(출력은 라벨)가 아닌 p(π∣x)p(\boldsymbol{\pi}|\bold{x})(출력은 분포)를 인코딩 하기 때문에 prior network라고 부른다.

참조

Made with