Search
Duplicate

수학/ Markov Chains

Definition

•
xt\bold{x}_t가 시스템의 상태에 관한 관련된 모든 정보를 포착한다고 가정하자. 이것은 주어진 과거가 미래를 예측하는 것에 대한 충분 통계량(sufficient statistic)이라는 뜻이다. 즉
p(xt+τ∣xt,x1:t−1)=p(xt+τ∣xt)p(\bold{x}_{t+\tau}|\bold{x}_t,\bold{x}_{1:t-1}) = p(\bold{x}_{t+\tau}|\bold{x}_t)
•
모든 τ≥0\tau \ge 0에 대해 이것은 Markov assumption이라고 부른다.
•
이 경우에 모든 유한 길이의 시퀀스에 대해 결합 분포를 다음과 같이 작성할 수 있다.
p(x1:T)=p(x1)p(x2∣x1)p(x3∣x2)p(x4∣x3)...=p(x1)∏t=2Tp(xt∣xt−1)p(\bold{x}_{1:T}) = p(\bold{x}_1)p(\bold{x}_2|\bold{x}_1)p(\bold{x}_3|\bold{x}_2)p(\bold{x}_4|\bold{x}_3)... = p(\bold{x}_1) \prod_{t=2}^T p(\bold{x}_t|\bold{x}_{t-1})
•
이것을 Markov chain 또는 Markov model이라 부른다.

Parameterization

Markov transition kernels

•
조건부 분포 p(xt∣xt−1)p(\bold{x}_t|\bold{x}_{t-1})은 transition function(전이 함수), transition kernel(전이 커널) 또는 Markov kernel이라 한다. 이것은 주어진 시간 t−1t-1의 상태에 대해 시간 tt의 상태에 대한 조건부 분포이다. 따라서 이것은 다음 두 조건을 만족한다.
p(xt∣xt−1)≥0∫x∈Xdx p(xt=x∣xt−1)=1\begin{aligned} p(\bold{x}_t|\bold{x}_{t-1}) &\ge 0 \\ \int_{\bold{x} \in \mathcal{X}} dx \ p(\bold{x}_t=\bold{x}|\bold{x}_{t-1})&=1 \end{aligned}
•
전이 함수 p(xt∣x1:t−1)p(\bold{x}_t|\bold{x}_{1:t-1})가 시간에 독립이면 모델은 homogeneous, stationary 또는 time-invariant라고 한다.
◦
이것은 같은 파라미터가 여러 변수에서 공유되기 때문에 parameter 묶음의 예이다. 이 가정을 통해 고정된 수의 파라미터를 사용하여 임의의 수의 변수를 모델링할 수 있다.

Markov transition matrices

•
변수가 이산이라고 가정한다. 따라서 Xt∈{1,...,K}X_t \in \{1,...,K\}. 이것은 finite-state Markov chain이라고 부른다.
◦
이 경우에 조건부 분포 p(Xt∣Xt−1)p(X_t|X_{t-1})는 transition matrix(전이 행렬)이라 부르는 K×KK \times K 행렬 A\bold{A}로 작성될 수 있다.
◦
여기서 Aij=p(Xt=j∣Xt−1=i)A_{ij} = p(X_t = j|X_{t-1} = i)는 상태 ii에서 상태 jj로 가는 확률이고, 행렬의 각 행의 합은 1이다. ∑jAij=1\sum_j A_{ij} = 1.
◦
따라서 이것을 stochastic matrix라고 부른다.
•
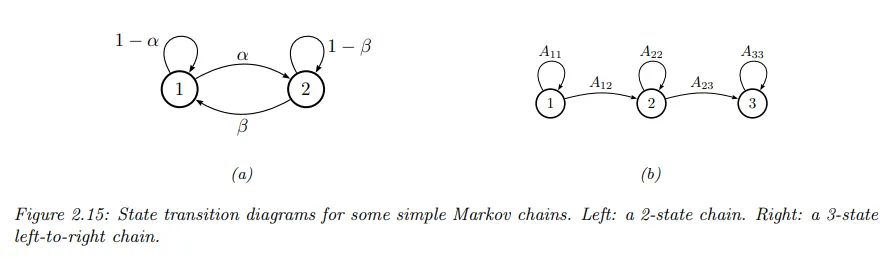
고정된 유한-상태 마르코프 체인은 stochastic automaton과 동등하다. 이런 automata를 시각화 하기 위해 노드로 상태를 표현하고 화살표로 적법한 전이, 즉 A\bold{A}의 0이 아닌 요소를 나타내는 방향성 그래프를 그리는 것이 일반적이다. 이것을 state transition diagram이라고 한다. 아래 그림 참조.
◦
arc와 관련된 가중치는 확률이다.
•
예컨대 2-state chain 다음과 같고
A=(1−ααβ1−β)\bold{A} = \begin{pmatrix} 1 - \alpha & \alpha \\ \beta & 1 - \beta \end{pmatrix}
•
3-state chain은 다음과 같다.
A=(A11A1200A22A23001)\bold{A} = \begin{pmatrix} A_{11} & A_{12} & 0 \\ 0 & A_{22} & A_{23} \\ 0 & 0 & 1 \end{pmatrix}
•
이것은 left-to-right transition matrix라고 한다.
•
전이 행렬의 AijA_{ij} 항목은 한 단계에서 ii에서 jj로 가는 확률을 지정한다. nn-단계 전이 행렬 A(n)\bold{A}(n)은 다음처럼 정의된다.
Aij(n)≜p(Xt+n=j∣Xt=i)A_{ij}(n) \triangleq p(X_{t+n} = j|X_t = i)
•
이것은 정확하게 nn 단계에서 ii에서 jj로 가는 확률이다. 분명히 A(1)=A\bold{A}(1) = \bold{A}이다.
•
Chapman-Kolmogorov 등식은 다음을 나타낸다.
Aij(m+n)=∑k=1KAik(m)Akj(n)A_{ij}(m+n) = \sum_{k=1}^K A_{ik}(m)A_{kj}(n)
•
즉 m+nm+n 단계에서 ii에서 jj로 가는 확률은 mm 단계에서 ii에서 kk로 가는 확률과 nn 단계에서 kk에서 jj로 가는 확률을 모든 kk에 대해 합산한 것이다. 이 내용을 행렬 곱으로 작성할 수 있다.
A(m+n)=A(m)A(n)\bold{A}(m+n) = \bold{A}(m)\bold{A}(n)
•
따라서
A(n)=AA(n−1)=AAA(n−2)=...=An\bold{A}(n) = \bold{AA}(n-1) = \bold{AAA}(n-2) = ... = \bold{A}^n
•
따라서 마르코프 체인의 여러 단계를 전이 행렬의 지수로 시뮬레이션 할 수 있다.

Higher-order Markov models

•
1차 마르코프 가정은 꽤 강력하다. 다행히 1차 모델을 마지막 nn개 관찰에 의존하도록 쉽게 일반화하여 차수 (메모리 길이) nn의 모델을 만들 수 있다.
p(x1:T)=p(x1:n)∏t=n+1Tp(xt∣xt−n:t−1)p(\bold{x}_{1:T}) = p(\bold{x}_{1:n}) \prod_{t=n+1}^T p(\bold{x}_t|\bold{x}_{t-n:t-1})
•
이것을 차수 nn의 마르코프 모델이라 부른다.
◦
n=1n=1이면 특성들의 쌍 p(xt∣xt−1)p(\bold{x}_t|\bold{x}_{t-1})을 표현해야 하기 때문에 bigram model이라 부른다.
◦
n=2n=2이면 특성들의 triple p(xt∣xt−1,xt−2)p(\bold{x}_t|\bold{x}_{t-1},\bold{x}_{t-2})을 표현해야 하기 때문에 trigram model이라 부른다.
◦
일반적으로 n-gram 모델이라 부른다.
•
그러나 과거 nn개 관찰을 포함하는 augmented 상태 공간을 정의하여 고차 마르코프 모델을 1차로 변환할 수 있다.
◦
예컨대 n=2n=2이면 x~t=(xt−1,xt)\tilde{\bold{x}}_t = (\bold{x}_{t-1},\bold{x}_t)을 정의하고 다음을 사용할 수 있다.
p(x~1:T)=p(x~2)∏t=3Tp(x~t∣x~t−1)=p(x1,x2)∏t=3Tp(xt∣xt−1,xt−2)p(\tilde{\bold{x}}_{1:T}) = p(\tilde{\bold{x}}_2)\prod_{t=3}^T p(\tilde{\bold{x}}_t|\tilde{\bold{x}}_{t-1}) = p(\bold{x}_1,\bold{x}_2)\prod_{t=3}^Tp(\bold{x}_t|\bold{x}_{t-1},\bold{x}_{t-2})

Parameter estimation

Maximum likelihood estimation

•
길이 TT의 임의의 특정한 시퀀스의 확률은 다음처럼 주어진다.
p(x1:T∣θ)=π(x1)A(x1,x2)...A(xT−1,xT)=∏j=1K(πj)I(x1=j)∏t=2T∏j=1K∏k=1K(Ajk)I(xt=k,xt−1=j)\begin{aligned} p(x_{1:T}|\boldsymbol{\theta}) &= \pi(x_1)A(x_1,x_2)...A(x_{T-1},x_T) \\ &= \prod_{j=1}^K (\pi_j)^{\mathbb{I}(x_1=j)} \prod_{t=2}^T\prod_{j=1}^K\prod_{k=1}^K(A_{jk})^{\mathbb{I}(x_t=k,x_{t-1}=j)}\end{aligned}
•
따라서 시퀀스의 집합 D=(x1,...,xN)\mathcal{D} = (\bold{x}_1,...,\bold{x}_N)의 (여기서 xi=(xi1,...,xi,Ti)\bold{x}_i = (x_{i1},...,x_{i,T_i})는 길이 TiT_i의 시퀀스) log likelihood는 다음과 같이 주어진다.
log⁡p(D∣θ)=∑i=1Nlog⁡p(xi∣θ)=∑jNj1log⁡πj+∑j∑kNjklog⁡Ajk\log p(\mathcal{D}|\boldsymbol{\theta}) = \sum_{i=1}^N \log p(\bold{x}_i|\boldsymbol{\theta}) = \sum_j N_j^1 \log \pi_j + \sum_j \sum_k N_{jk} \log A_{jk}
•
여기서 다음의 count를 정의한다.
Nj1≜∑i=1NI(xi1=j)Njk≜∑i=1N∑t=1Ti−1I(xi,t=j,xi,t+1=k)Nj=∑kNjk\begin{aligned} N_j^1 &\triangleq \sum_{i=1}^N \mathbb{I}(x_{i1} = j) \\ N_{jk} &\triangleq \sum_{i=1}^N\sum_{t=1}^{T_i-1} \mathbb{I}(x_{i,t}=j,x_{i,t+1}=k)\\N_j &= \sum_k N_{jk} \end{aligned}
•
라그랑지안 승수를 추가하여 합해서 1이 되는 제약조건을 강제하면 MLE가 normalized counts 의해 주어짐을 보일 수 있다.
π^j=Nj1∑j′Nj′1,A^jk=NjkNj\hat{\pi}_j = {N_j^1 \over \sum_{j'} N_{j'}^1}, \hat{A}_{jk} = {N_{jk} \over N_j}
•
종종 시퀀스의 시작에서 기호 jj가 나타나는 빈도를 나타내는 Nj1N_j^1을 수열의 어느 곳에서나 기호 jj가 나타나는 빈도를 나타내는 NjN_j로 대체한다. 이렇게 하면 단일 시퀀스에서 매개변수를 추정할 수 있다.
•
counts NjN_j는 unigram statics라고 하고 NjkN_{jk}는 bigram statistics라고 한다.

Sparse data problem

•
큰 nn에 대해 n-gram 모델을 시도할 때 데이터 희소성 때문에 과적합 문제에 빠르게 맞닥뜨리게 된다.
◦
jj개 크기 Kn−1K^{n-1}의 이산 맥락에 대해 인덱싱하기 때문에 많은 예상 카운트 NjkN_{jk}가 0이 될 것이며, 이는 점점 더 드물어질 것이다.
◦
bigram 모델(n=2n=2)의 경우에도 KK가 크면 문제가 발생할 수 있다. 예컨대 어휘에 K∼50000K \sim 50000개의 단어가 있는 경우 bi-gram 모델은 가능한 모든 단어 쌍에 해당하는 25억개의 자유 파라미터를 갖게 된다. 훈련 데이터에서 이것을 볼 가능성은 거의 없다. 그러나 훈련 데이터에서 보지 못했다고해서 특정 단어의 문자열이 완전히 불가능하다고 예측하는 것은 심각한 형태의 과적합이 될 수 있다.
•
이 문제에 대한 ‘무차별 대입’의 해결책은 많은 데이터를 수집하는 것이다.
◦
예컨대 Google은 웹에서 추출한 1조 개의 단어를 기반으로 n-gram 모델(n=1:5n = 1:5)을 맞췄다. 이 데이터는 압축되지 않은 상태로 100GB가 넘으며 공개적으로 사용 가능하다.
◦
이러한 접근 방식은 놀라울 정도로 성공적일 수 있지만 인간은 훨씬 적은 데이터로 학습할 수 있기 때문에 다소 불만족스럽다.

MAP estimation

•
희소 데이터 문제에 대한 한가지 단순한 해결책은 균등 디리클레 prior Aj:∼Dir(α1)\bold{A}_{j:} \sim \text{Dir}(\alpha\bold{1})의 MAP 추정을 사용하는 것이다. 이 경우에 MAP 추정은 다음과 같다.
A^jk=Njk+αNj+Kα\hat{A}_{jk} = {N_{jk} +\alpha \over N_j + K\alpha}
•
α=1\alpha=1이면 이것은 add-one smoothing이라고 부른다.
•
add-one smoothing의 주요 문제는 이것이 n-gram이 동등한 가능성을 갖는다고 가정하는 것이다. 이것은 매우 비현실적이다. 더 정교한(sohpisticated) 접근은 계층적 베이즈에 기반한 것이다.

Stationary distribution of a Markov chain

•
마르코프 체인으로부터 연속적인 샘플을 계속 뽑는다고 가정하자. 유한 상태 공간의 경우에 이것을 하나의 상태를 다른 것으로 ‘hopping’하는 것으로 생각할 수 있다.
◦
전이 그래프에 따라 어떤 상태는 다른 것보다 더 많은 시간을 소모하는 경향이 있다. 상태에 대한 long term 분포는 체인의 고정 분포(stationary distribution)라고 한다.

What is a stationary distribution?

•
Aij=p(Xt=j∣Xt−1=i)A_{ij} = p(X_t = j|X_{t-1}=i)를 한 단계 전이 행렬이라고 하고 πt(j)=p(Xt=j)\pi_t(j) = p(X_t = j)를 시간 tt에서 상태 jj에 있을 확률이라 하자.
•
π0\boldsymbol{\pi}_0의 상태들에 대한 초기 분포를 가지면 시간 11에서 다음을 갖는다.
π1(j)=∑iπ0(i)Aij\pi_1(j) = \sum_i \pi_0(i) A_{ij}
•
또는 행렬 표기에서 π1=π0A\boldsymbol{\pi}_1 = \boldsymbol{\pi}_0\bold{A}.
◦
여기서 가정 π\boldsymbol{\pi}는 표준 관례에 따라 행 벡터이고 따라서 전이 행렬을 뒤에 곱한다.
•
이제 이 방정식을 반복하는 것을 상상하자. 만일 π=πA\boldsymbol{\pi} = \boldsymbol{\pi}\bold{A}인 상태에 도달하면 고정 분포(stationary distribution)에 도달했다고 말한다. 고정 분포에 진입하면 절대로 떠나지 않는다.
◦
고정 분포는 invariant distribution(불변 분포) 또는 equilibrium distribution(평형 분포)이라고도 한다.
•
예컨대 아래 그림의 체인을 고려하자.
•
고정 분포를 찾기 위해 다음과 같이 작성한다.
(π1π2π3)=(π1π2π3)(1−A12−A13A12A13A211−A21−A23A23A31A321−A31−A32)\begin{pmatrix} \pi_1 & \pi_2 & \pi_3 \end{pmatrix} = \begin{pmatrix} \pi_1 & \pi_2 & \pi_3 \end{pmatrix}\begin{pmatrix} 1-A_{12}-A_{13} & A_{12} & A_{13} \\ A_{21} & 1-A_{21}-A_{23} & A_{23} \\ A_{31} & A_{32} & 1-A_{31}-A_{32} \end{pmatrix}
•
따라서 π1(A12+A13)=π2A21+π3A31\pi_1(A_{12}+A_{13}) = \pi_2A_{21} + \pi_3A_{31}.
•
일반적으로 다음을 갖는다.
πi∑j≠iAij=∑j≠iπjAji\pi_i \sum_{j\ne i}A_{ij} = \sum_{j\ne i} \pi_j A_{ji}
•
즉 상태 ii에 있을 확률과 상태 ii에서 나가는 순 흐름(net flow)의 곱은 다른 상태 jj에 있을 확률과 해당 상태에서 ii로 들어오는 순 흐름을 곱한 값과 같아야 한다. 이것을 global balance equation라고 한다.
◦
그런 다음 ∑jπj=1\sum_j \pi_j = 1이라는 제약조건 하에 이 방정식을 불편 아래에서 설명하는 것처럼 고정 분포를 구할 수 있다.

Computing the stationary distribution

•
고정 분포를 찾기 위해 고유벡터 방정식 A⊤v=v\bold{A}^\top \bold{v} = \bold{v}를 풀고 π=v⊤\boldsymbol{\pi} = \bold{v}^\top를 설정하면 된다. 여기서 v\bold{v}는 고윳값이 11인 고유벡터이다.
◦
A\bold{A}가 행-확률 행렬이고 따라서 A1=1\bold{A1} = \bold{1}이기 때문에 고유벡터가 존재하는 것을 확실히 할 수 있다. 또한 A\bold{A}와 A⊤\bold{A}^\top의 고유값들이 같음을 떠올려라.
◦
물론 고유벡터들이 비례 원칙의 상수까지만 고유하므로 마지막에 v\bold{v}를 정규화해서 합이 1이 되도록 해야 한다.
•
그러나 행렬의 모든 항목이 엄격하게(strictly) positive Aij>0A_{ij} > 0인 경우에만 고유벡터들은 실수값이어야 보장된다. (합해서 1이 되어야 하기 때문에 Aij<1A_{ij} < 1).
◦
전이 확률이 00이나 11인 체인을 다룰 수 있는 더 일반적인 접근은 다음과 같다. π(I−A)=0K×1\boldsymbol{\pi}(\bold{I}-\bold{A}) = \bold{0}_{K\times1}에서 KK개 제약조건과 π1K×1=1\boldsymbol{\pi}\bold{1}_{K\times1} = 1에서 11개 제약조건을 갖는다. 따라서 πM=r\boldsymbol{\pi}\bold{M} = \bold{r}을 풀어야 한다.
◦
여기서 M=[I−A,1]\bold{M} = [\bold{I}- \bold{A},\bold{1}]는 K×(K+1)K \times (K+1) 행렬이고 r=[0,0,...,0,1]\bold{r} = [0,0,...,0,1]은 1×(K+1)1\times (K+1) 벡터이다.
◦
그러나 이것은 과한 제약조건이다. 따라서 M\bold{M}의 정의에서 I−A\bold{I}-\bold{A}의 마지막 컬럼을 제외하고 r\bold{r}의 마지막 00을 제거한다. 예컨대 3개 상태 체인에 대해 다음의 선형 시스템을 해결해야 한다.
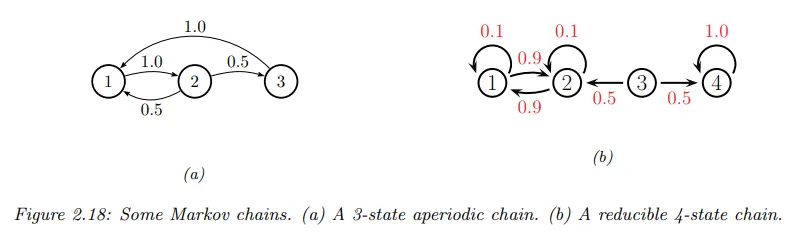
(π1π2π3)(1−A11−A121−A211−A221−A31−A321)=(001)\begin{pmatrix} \pi_1 & \pi_2 & \pi_3 \end{pmatrix}\begin{pmatrix} 1 - A_{11} & -A_{12} & 1 \\ -A_{21} & 1-A_{22} & 1 \\ -A_{31}& -A_{32} & 1 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 1\end{pmatrix}
•
앞선 그림 (a)의 체인의 경우 π=[0.4,0.4,0.2]\boldsymbol{\pi} = [0.4,0.4,0.2]를 찾을 수있다. π=πA\boldsymbol{\pi} = \boldsymbol{\pi}\bold{A}이기 때문에 이것이 올바르다는 것을 쉽게 확인할 수 있다.

When does a stationary distribution exist?

•
불행히도 모든 체인이 고정 분포를 갖는 것은 아니다. 앞선 그림 (b)의 4개 상태 체인를 고려하자.
◦
state 4에서 시작하면 4가 absorbing state이기 때문에 영원이 거기에 머무를 수 있다. 따라서 π=(0,0,0,1)\boldsymbol{\pi} = (0,0,0,1)은 하나의 가능한 고정 분포이다.
◦
그러나 1이나 2에서 시작하면 이 2개 상태를 영원히 왔다갔다(oscillate) 하게 된다. 따라서 π=(0.5,0.5,0,0)\boldsymbol{\pi} = (0.5,0.5,0,0)는 또 다른 가능한 고정 분포이다.
◦
3에서 시작하면 동등한 확률로 위의 고정 분포 중 하나에 도달할 수 있다. 해당하는 전이 그래프는 서로 분리된 2개의 연결 구성요소가 있다.
•
이 예제에서 하나의 고정 분포를 갖는 필요 조건은 상태 전이 다이어그램이 단일 연결된 구성요소여야 한다는 것을 볼 수 있다. 즉 임의의 상태에서 다른 임의의 상태로 이동할 수 있다. 이런 체인은 irreducible(환원 불가능)이라고 한다.
•
이제 2개 상태 체인의 그림의 경우를 고려하자.
◦
이것은 α,β>0\alpha, \beta > 0에서 환원 불가능하다.
◦
α=β=0.9\alpha= \beta = 0.9를 가정하면 이 체인은 각 상태에서 시간의 50%를 사용하는 대칭임이 분명하다. 따라서 π=(0.5,0.5)\boldsymbol{\pi} = (0.5,0.5)이다.
◦
α=β=1\alpha= \beta = 1을 가정하면 체인은 두 상태 사이를 왔다갔다 하지만 어디에서 시작했는지에 따라 long-term 분포가 달라진다. 상태 1에서 시작했다면 매 홀수 단계 (1,3,5,…)에서 상태 1일 것이고, 상태 2에서 시작했다면 매 홀수 단계에서 상태 2일 것이다.
•
이 예제는 다음의 정의에 동기를 부여한다.
◦
πj=lim⁡n→∞Aijn\pi_j = \lim_{n\to \infty} A_{ij}^n이 존재하고 모든 jj에 대해 시작 상태 ii가 독립이면 체인은 limiting distribution(극한 분포)을 갖는다고 할 수 있다. 이것을 성립하면 상태에 대한 long-run 분포는 시작 상태에 독립이다.
p(Xt=j)=∑ip(X0=i)Aij(t)→πj as t→∞p(X_t = j) = \sum_i p(X_0 =i)A_{ij}(t) \to \pi_j \text{ as } t \to \infty
•
이제 극한 분포가 존재할 때 특성화를 하자. 상태 ii의 period(주기)를 아래와 같이 정의한다.
◦
여기서 gcd는 greatest common divisor(최대공약수)의 약자이다. 즉 집합의 모든 멤버로 나누는 가장 큰 정수이다.
d(i)≜gcd{t:Aii(t)>0}d(i) \triangleq \text{gcd}\{t: A_{ii}(t) > 0 \}
•
예컨대 앞선 그림 (a)에서 d(1)=d(2)=gcd(2,3,4,6,...)=1d(1) = d(2) = \text{gcd}(2,3,4,6,...) = 1이고 d(3)=gcd(3,5,6,...)=1d(3) = \text{gcd}(3,5,6,...)=1이다.
•
d(i)=1d(i) = 1이면 ii가 aperiodic(비주기적)이라 한다.
◦
이것을 보장하기 위한 충분 조건은 상태 ii가 self-loop인 것이다. 그러나 이것은 필요 조건은 아니다.
•
체인의 모든 상태가 비주기적이면 체인이 비주기적이다고 한다. 이것은 다음의 중요한 결과를 보일 수 있다.
Theorem 모든 환원 불가능한 (단일 연결), 비주기적 유한 상태 마르코프 체인은 고유한 고정 분포인(unique stationary distribution) π\boldsymbol{\pi}와 같은 극한 분포(limiting distribution)를 갖는다.
•
이 결과의 특별한 경우는 모든 regular 유한 상태 체인이 고유한 고정 분포를 갖는다고 말한다.
◦
여기서 regular 체인은 어떤 정수 nn과 모든 i,ji,j에 대해 Aijn>0A_{ij}^n > 0을 만족하는 전이 행렬이다. 즉 이것은 nn 단계에서 모든 상태에서 다른 모든 상태로 전이할 수 있다.
◦
결론적으로 nn 단계 후에 체인은 어디에서 시작했든지 모든 상태가 될 수 있다. regularity를 보장하는 충분 조건은 체인이 환원 불가능(단일 연결)이고 모든 상태는 self-transition를 갖는다는 것을 보일 수 있다.
•
상태 공간이 유한하지 않은(즉 모든 정수의 countable set이거나 모든 실수의 uncountable set) 마르코프 체인의 경우를 다루기 위해 앞선 정의를 일부 일반화 해야 한다.
◦
상세한 내용이 상당히 기술적이기 때문에 증명 없이 주요 결과만 간략히 소개한다.
•
고정 분포가 존재하려면 이전과 마찬가지로 환원 불가능(단일 연결)과 비주기성이 필요하고 추가로 각 상태가 recurrent(반복적) 라는 것이 필요하다. 이것은 확률 1의 상태로 돌아간다는 것을 의미한다.
◦
non-recurrent 상태(즉 transient(일시적인) state)의 단순한 예로 앞선 그림 (b)를 고려하자. 상태 3은 임시적이다. 왜냐하면 이 상태에서 벗어나면 상태 4 주위를 영원히 돌거나 상태 1과 2사이를 영원히 왔다갔다 하기 때문이다. 따라서 상태 3으로 돌아오는 방법이 없다.
•
모든 유한 상태 환원 불가능한 체인은 recurrent임이 분명하다. 어디에서 시작했든지 항상 돌아올 수 있기 때문이다.
•
그러나 무한 상태 공간을 고려하자. 정수 X={...,−2,−1,0,1,2,...}\mathcal{X} = \{...,-2,-1,0,1,2,...\}에서 랜덤 워크를 수행한다고 가정하고 Ai,i+1=pA_{i,i+1} = p을 오른쪽으로 이동할 확률이라고 하고 Ai,i−1=1−pA_{i,i-1} = 1-p를 왼쪽으로 이동할 확률이라 하자.
◦
X1=0X_1 = 0에서 시작한다고 할 때, p>0.5p > 0.5이면 +∞+\infty로 발사되고 돌아온다고 보장할 수 없다. 마찬가지로 p<0.5p<0.5이면 −∞-\infty로 발사된다. 따라서 두 경우 모두 환원 불가능하지만 체인은 recurrent가 아니다.
◦
한편 p=0.5p=0.5이면 확률 1로 초기 상태로 되돌아올 수 있으므로 체인은 recurrent이다. 그러나 분포는 점점 더 큰 정수 집합에 걸쳐 계속 퍼져 나가기 때문에 돌아오는데 걸리는 기대 시간은 무한이다. 이것은 체인이 고정 분포를 갖지 못하게 한다.
•
더 형식적으로 상태가 돌아오는 기대 시간이 유한이면 상태를 non-null recurrent로 정의할 수 있다. 상태가 비주기적, recurrent, non-null이면 상태를 ergodic(에르고딕)이라고 할 수 있다.
◦
모든 상태가 에르고딕이면 체인이 에르고딕이라고 할 수 있다. 이 정의를 통해 주요 theorem을 서술할 수 있다.
Theorem 모든 환원 불가능, 에르고딕 마르코프 체인은 고유한 고정 분포인 π\boldsymbol{\pi}와 같은 극한 분포를 갖는다.

Detailed balance

•
에르고딕을 설립하는 것은 어렵기 때문에 확인하기 더 쉬운 대안 조건을 제공한다. 만일 다음과 같은 분포 π\boldsymbol{\pi}가 존재하면 마르코프 체인 A\bold{A}는 time reversible(가역적)이라고 한다.
πiAij=πjAji\pi_i A_{ij} = \pi_j A_{ji}
•
이것은 detailed balance equation이라 한다. 이것은 ii에서 jj로의 흐름이 적절한 source 확률로 가중치를 부여한 jj에서 ii로의 흐름과 같아야 한다는 것을 말한다.
◦
다음의 중요한 결과를 얻는다.
Theorem 전이 행렬 A\bold{A}의 마르코프 체인이 regular이고 분포 π\boldsymbol{\pi}에 대해 detailed balance equation을 만족하면 π\boldsymbol{\pi}는 체인의 고정 분포이다.
•
증명) 이것을 보기 위해 다음에 유의하라.
∑iπiAij=∑iπjAji=πj∑iAji=πj\sum_i \pi_iA_{ij} = \sum_i\pi_j A_{ji} = \pi_j \sum_iA_{ji} = \pi_j
•
따라서 π=Aπ\boldsymbol{\pi} = \bold{A}\boldsymbol{\pi}
•
이 조건이 충분하지만 필요는 아님에 유의하라.
◦
detailed balance를 만족하지 않는 고정 분포의 체인의 예제에 대해 위 그림 (a) 참조.

참고

Made with