Search
Duplicate

AI/ Variational Auto Encoder(VAE)

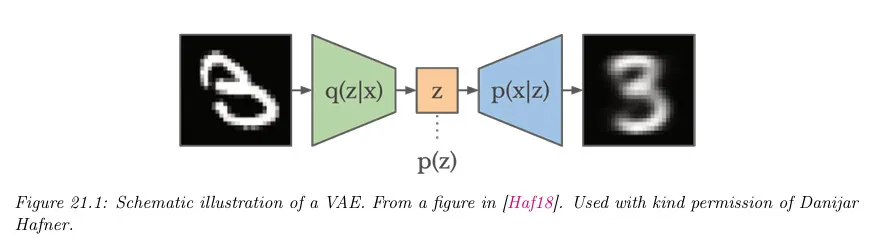
Variational Auto Encoder(VAE)

Auto Encoder(AE)는 결정론적인 모델이라 생성 모델로 쓰기에는 결과가 좋지 않았음. 더 나은 데이터 생성을 결과를 얻기 위해 AE를 확률적 버전으로 구성한 것이 VAE라고 볼 수 있다.
AE를 확률론적 버전으로 구성할 때 encoder를 단순히 p(z)p(\bold{z})로 구성하면 생성 결과가 좋지 못하기 때문에 p(z∣x)p(\bold{z}|\bold{x})와 같이 조건부 형태로 구성 한다. 이때 p(z∣x)p(\bold{z}|\bold{x})의 posterior를 계산하기 위한 marginal likelihood p(x)p(\bold{x})를 직접 계산하는 것이 어렵기 때문에 Variational Inference을 사용하여 계산하기 쉬운 (일반적으로 가우시안인) q(z∣x)q(\bold{z}|\bold{x})를 정의하고 KL divergence로 이 분포를 p(z∣x)p(\bold{z}|\bold{x})와 가깝게 만드는 방법을 사용함. (물론 가우시안인 아닌 p(z∣x)p(\bold{z}|\bold{x})를 가우시안인 q(z∣x)q(\bold{z}|\bold{x})로 근사하는 것은 한계가 있다. 이것이 Variational 방법의 한계 중 하나이다.)
최종적으로 VAE의 encoder는 qϕ(z∣x)q_{\boldsymbol{\phi}}(\bold{z}|\bold{x})의 형식을 갖고 decoder는 pθ(x∣z)p_{\boldsymbol{\theta}}(\bold{x}|\bold{z})의 형식을 갖게 됨.
VAE의 손실 함수는 여러가지 형태로 기술할 수 있지만 간단히 정리하면 다음과 같다.
L=−Eq(z∣x)[log⁡p(x∣z)]+KL(q(z∣x)∥p(z))\mathcal{L} = -\mathbb{E}_{q(\bold{z}|\bold{x})}[\log p(\bold{x}|\bold{z})] + \text{KL}(q(\bold{z}|\bold{x})\|p(\bold{z}))
여기서 −Eq(z∣x)[log⁡p(x∣z)]-\mathbb{E}_{q(\bold{z}|\bold{x})}[\log p(\bold{x}|\bold{z})]는 reconstruction error로 encoder가 생성한 잠재 변수 z\bold{z}를 기반으로 원본 x\bold{x}를 얼마나 잘 재구성하는지를 측정하는 것으로 디코더의 성능을 평가하는 부분으로 볼 수 있다. 일반적으로 cross entropy를 사용함.
KL(q(z∣x)∥p(z))\text{KL}(q(\bold{z}|\bold{x})\|p(\bold{z}))는 q(z∣x)q(\bold{z}|\bold{x})가 근사하려는 p(z∣x)p(\bold{z}|\bold{x})에 얼마나 가까운지를 측정하는 것으로 인코더의 성능을 평가하는 부분으로 볼 수 있다. 일반적으로 p(z)∼N(0,I)p(\bold{z}) \sim \mathcal{N}(\bold{0}, \bold{I})를 사용. q(z∣x)q(\bold{z}|\bold{x})가 근사하려던 원래 분포가 p(z∣x)p(\bold{z}|\bold{x})였는데 KL divergence에 p(z)p(\bold{z})가 쓰이는 이유는 VAE의 손실 함수 유도과정 때문이다. 아래 참고 자료의 <시각적 이해를 위한 머신러닝> 참조.
참고로 VAE의 encoder가 출력하는 잠재 변수 z\bold{z}의 평균 μ\mu과 분산 σ2\sigma^2을 이용하여 KL divergence를 다음과 같이 계산할 수 있다. 아래 식에서 JJ는 잠재 변수의 차원이다.
KL(q(z∣x)∥p(z))=−12∑j=1J(1+log⁡(σj2)−μj2−σj2)\text{KL}(q(\bold{z}|\bold{x})\|p(\bold{z})) = -{1\over2} \sum_{j=1}^J (1 + \log(\sigma_j^2) - \mu_j^2 - \sigma_j^2)

β\beta-VAE

VAE의 단점은 생성된 이미지가 blur 이미지가 되는 경향이 있다는 것이다. 이것을 보완하기 위해 여러 방법을 사용할 수 있지만, 간단한 방법은 KL 항에 페널티를 감소시켜서 모델을 결정론적 autoencoder에 더 가깝게 만드는 것이다.
Lβ(θ,ϕ∣x)=−Eqϕ(z∣x)[log⁡pθ(x∣z)]⏟LE+βDKL(qϕ(z∣x)∥pθ(z))⏟LR\mathcal{L}_\beta(\boldsymbol{\theta},\boldsymbol{\phi}|\bold{x}) = \underbrace{-\mathbb{E}_{q_{\boldsymbol{\phi}}(\bold{z}|\bold{x})}[\log p_{\boldsymbol{\theta}}(\bold{x}|\bold{z})]}_{\mathcal{L}_E} + \beta\underbrace{D_\text{KL}(q_{\boldsymbol{\phi}}(\bold{z}|\bold{x})\|p_{\boldsymbol{\theta}}(\bold{z}))}_{\mathcal{L}_R}
여기서 LE\mathcal{L}_E는 reconstruction 에러(negative log likelihood)이고 LR\mathcal{L}_R은 KL regularizer이다. 이것을 β\beta-VAE 목적이라고 한다. β=1\beta=1을 설정하면 표준 VAEs에서 사용되는 목적을 복구한다. β=0\beta=0을 설정하면 표준 autoencoder에서 사용되는 목적을 복구한다.
β\beta를 0에서 무한대로 변화시키면 rate distortion curve의 다양한 지점에 도달하게 된다. 이러한 점들은 reconstruction error(distortion)과 입력에 관한 잠재에 저장된 정보의 양(코드에 해당하는 rate) 사이의 다양한 tradeoff를 만든다. β<1\beta < 1을 사용하면 각 입력에 대해 더 많은 bit를 저장하므로 reconstruct 이미지는 덜 blur가 되고, β>1\beta>1을 사용하면 더 압축된 표현을 얻는다.

InfoVAE

VAE를 학습하는데 디코더가 강력하면 잠재 코드가 무시되는 경향이 있고 데이터 공간과 잠재 공간에서 KL 항 사이의 불일치 때문에 빈곤한 posterior 근사를 하는 경향이 있다. 다음 형식의 일반화된 목적을 사용하여 어떤 정도로 이 문제를 수정할 수 있다.
Ł(θ,ϕ∣x)=−λDKL(qϕ(z)∥pθ(z))−Eqϕ(z)[DKL(qϕ(x∣z)∥pθ(x∣z))]+αIq(x;z)Ł(\boldsymbol{\theta},\boldsymbol{\phi}|\bold{x}) = -\lambda D_\text{KL}(q_{\boldsymbol{\phi}}(\bold{z})\|p_{\boldsymbol{\theta}}(\bold{z})) - \mathbb{E}_{q_{\boldsymbol{\phi}}(\bold{z})}[D_\text{KL}(q_{\boldsymbol{\phi}}(\bold{x}|\bold{z})\|p_{\boldsymbol{\theta}}(\bold{x}|\bold{z}))] + \alpha \mathbb{I}_q(\bold{x};\bold{z})
여기서 α≥0\alpha \ge 0은 x\bold{x}와 z\bold{z} 사이의 상호 정보량 Iq(x;z)\mathbb{I}_q(\bold{x};\bold{z})에 가중치를 얼마나 부여할지 제어한다. λ≥0\lambda \ge 0는 z\bold{z}-공간 KL과 x\bold{x}-공간 KL 사이의 tradeoff를 제어한다. 이것을 InfoVAE 목적이라고 한다. α=0\alpha=0과 λ=1\lambda=1을 설정하면 표준 ELBO를 복구한다. 불행히 이 방정식의 목적은 MI 항이 까다롭기 때문에 작성한대로 계산할 수 없다. 이에 대한 내용은 생략. 더 자세한 내용은 참고 자료의 <PML: Advanced Topic> 참조.

Sample Code

Model

간단한 VAE 모델 구성. 아래 예시 코드를 보면 평균과 log 분산을 계산을 통해 구하지 않고 별도의 nn.Linear를 통과시켜서 구하도록 구성되어 있다. 이렇게 하면 두 레이어가 이후의 reparameterize 연산에 연결되어서 각각 평균과 log 분산을 학습하도록 된다고 하는데, 사실 납득은 잘 안 감.
추가로 잠재 변수 z를 z까지 신경망을 구성하지 않고 encode 까지의 신경망의 평균과 분산을 이용해서 reparameterize로 구한다.
# VAE 모델 정의 class VAE(nn.Module): def __init__(self): super(VAE, self).__init__() self.fc1 = nn.Linear(784, 400) self.fc21 = nn.Linear(400, 20) # 평균을 위한 레이어 self.fc22 = nn.Linear(400, 20) # 로그 분산을 위한 레이어 self.fc3 = nn.Linear(20, 400) self.fc4 = nn.Linear(400, 784) def encode(self, x): h1 = F.relu(self.fc1(x)) return self.fc21(h1), self.fc22(h1) def reparameterize(self, mu, logvar): std = torch.exp(0.5*logvar) eps = torch.randn_like(std) # 크기가 std인 평균 0, 표준편차 1의 가우시안 return mu + eps*std def decode(self, z): h3 = F.relu(self.fc3(z)) return torch.sigmoid(self.fc4(h3)) def forward(self, x): mu, logvar = self.encode(x.view(-1, 784)) z = self.reparameterize(mu, logvar) # encode의 평균과 분산을 이용해서 reparameterize로 잠재변수 z를 구한다. return self.decode(z), mu, logvar
Python
복사

Objective

VAE의 손실 함수
# 손실 함수 def loss_function(recon_x, x, mu, logvar): # 원본 입력과 reconstruction 사이의 binary cross entropy BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction='sum') # q(z|x)와 p(z)의 KL divergence. 잠재 변수 z의 평균과 분산을 이용해서 구한다. KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp()) return BCE + KLD
Python
복사

Train, Test

학습과 테스트 코드
import torch import torch.nn as nn import torch.nn.functional as F from torch.utils.data import DataLoader from torchvision import datasets, transforms from torchvision.utils import save_image import os # 데이터셋 로드 및 전처리 transform = transforms.Compose([ transforms.ToTensor(), ]) train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform) test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform) train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True) test_loader = DataLoader(test_dataset, batch_size=128, shuffle=False) # 'results' 디렉토리가 없으면 생성 if not os.path.exists('results'): os.makedirs('results') # 모델, 옵티마이저 설정 model = VAE() optimizer = torch.optim.Adam(model.parameters(), lr=1e-3) # 학습 함수 def train(epoch): model.train() train_loss = 0 for batch_idx, (data, _) in enumerate(train_loader): optimizer.zero_grad() recon_batch, mu, logvar = model(data) loss = loss_function(recon_batch, data, mu, logvar) loss.backward() train_loss += loss.item() optimizer.step() if batch_idx % 100 == 0: print(f"Train Epoch: {epoch} [{batch_idx * len(data)}/{len(train_loader.dataset)} ({100. * batch_idx / len(train_loader):.0f}%)]\tLoss: {loss.item() / len(data):.6f}") print(f'====> Epoch: {epoch} Average loss: {train_loss / len(train_loader.dataset):.4f}') # 테스트 함수 def test(epoch): model.eval() test_loss = 0 with torch.no_grad(): for data, _ in test_loader: recon, mu, logvar = model(data) test_loss += loss_function(recon, data, mu, logvar).item() test_loss /= len(test_loader.dataset) print(f'====> Test set loss: {test_loss:.4f}') # 학습 및 테스트 실행 for epoch in range(1, 11): train(epoch) test(epoch) with torch.no_grad(): sample = torch.randn(64, 20) sample = model.decode(sample).cpu() save_image(sample.view(64, 1, 28, 28), f'results/sample_{epoch}.png')
Python
복사
•
아래는 테스트 결과. 10번 정도의 epoch으로는 학습이 크게 되지 않기는 하지만 10번의 결과가 좀 더 선명해 보임
•
epoch 1
•
epoch 10

참고

Made with