Search
Duplicate

수학/ Bayesian Statistics - MLE, MAP, Credible Intervals

Bayesian statistics

•
통계에 대한 베이지안 접근에서 파라미터 θ\boldsymbol{\theta}를 미지수로 다루고, 데이터 D\mathcal{D}가 알려지고 고정되었다고 한다. 데이터를 본 한 후에 (사후에) 베이즈 룰을 사용하여 posterior 분포를 계산함으로써 파리미터에 관한 불확실성을 표현한다.
◦
베이지안 접근은 데이터를 관찰하면서 현재 확률 분포를 지속적으로 업데이트하는 것이고, 빈도주의의 접근은 데이터를 관찰하면서 현실을 정확히 표현하는 어떤 이상적인 확률 분포를 찾는 것이고 할 수 있다.
p(θ∣D)=p(θ)p(D∣θ)p(D)=p(θ)p(D∣θ)∫p(θ′)p(D∣θ′)dθ′p(\boldsymbol{\theta}|\mathcal{D}) = {p(\boldsymbol{\theta})p(\mathcal{D}|\boldsymbol{\theta}) \over p(\mathcal{D})} = {p(\boldsymbol{\theta})p(\mathcal{D}|\boldsymbol{\theta}) \over \int p(\boldsymbol{\theta}')p(\mathcal{D}|\boldsymbol{\theta}')d\boldsymbol{\theta}'}
•
여기서 p(θ)p(\boldsymbol{\theta})는 prior라고 하며 데이터를 보기 전에 파라미터에 대한 믿음(belief)를 표현한다.
◦
p(D∣θ)p(\mathcal{D}|\boldsymbol{\theta})는 likelihood라고 하며 각 파라미터의 설정에 대해 어떤 데이터가 나올 것이라고 예상하는지에 대한 믿음이다.
◦
p(θ∣D)p(\boldsymbol{\theta}|\mathcal{D})는 posterior라고 하며 데이터를 본 후에 파라미터에 관한 믿음을 표현한다.
◦
p(D)p(\mathcal{D})는 marginal likelihood 또는 evidence라고 하고 정규화 상수이다.
•
이 posterior를 계산하는 작업을 Bayesian inference, posterior inference 또는 그냥 inference라고 한다.

Maximum Likelihood Estimation(MLE)

•
Likelihood를 최대화하는 파라미터 θ\boldsymbol{\theta}를 찾는 것이 Maximum Likelihood Estimation(MLE)이다. 이 결과는 Likelihood의 최빈값(Mode)가 된다.
θ^=arg max⁡θp(D∣θ)\hat{\boldsymbol{\theta}} = \argmax_{\boldsymbol{\theta}} p(\mathcal{D}|\boldsymbol{\theta})

Maximum A Posterior(MAP)

•
Posterior를 최대화하는 파라미터 θ\boldsymbol{\theta}를 찾는 것이 Maximum A Posterior(MAP)이다. 이 결과는 posterior의 최빈값(Mode)가 된다.
θ^=arg max⁡θp(θ∣D)\hat{\boldsymbol{\theta}} = \argmax_{\boldsymbol{\theta}} p(\boldsymbol{\theta}|\mathcal{D})
•
posterior가 prior와 likelihood의 곱으로 표현가능하기 때문에 MAP은 다음과 같이 표현할 수 있다.
arg max⁡θp(θ∣D)∝arg max⁡θ(p(θ)×p(D∣θ))\argmax_{\boldsymbol{\theta}} p(\boldsymbol{\theta}|\mathcal{D}) \propto \argmax_{\boldsymbol{\theta}} \left( p(\boldsymbol{\theta}) \times p(\mathcal{D}|\boldsymbol{\theta}) \right)
•
일반적으로는 log를 취해 다음과 같이 표현한다.
arg max⁡θlog⁡p(θ∣D)∝arg max⁡θ(log⁡p(θ)+log⁡p(D∣θ))\argmax_{\boldsymbol{\theta}} \log p(\boldsymbol{\theta}|\mathcal{D}) \propto \argmax_{\boldsymbol{\theta}} \left( \log p(\boldsymbol{\theta}) + \log p(\mathcal{D}|\boldsymbol{\theta}) \right)

Marginal Likelihood

•
marginal likelihood p(D)p(\mathcal{D})는 연관된 prior와 함께 관찰된 데이터를 얼마나 잘 설명하느냐를 평가하는데 사용된다. 고로 베이지안 모델 선택에서 marginal likelihood가 가장 높은 모델을 선택하게 됨.
•
posterior를 p(θ∣D)∝p(θ)×p(D∣θ)p(\boldsymbol{\theta}|\mathcal{D}) \propto p(\boldsymbol{\theta}) \times p(\mathcal{D}|\boldsymbol{\theta})로 표현하는 것과 유사하게, marginal likelihood에 대해 다음처럼 계산할 수 있다.
◦
위는 이산인 경우, 아래는 연속인 경우
p(D)=∑θ[p(D∣θ)×p(θ)]p(D)=∫[p(D∣θ)×p(θ)]dθ\begin{aligned} p(\mathcal{D}) &= \sum_{\boldsymbol{\theta}} [p(\mathcal{D}|\boldsymbol{\theta}) \times p(\boldsymbol{\theta})] \\ p(\mathcal{D}) &= \int [p(\mathcal{D}|\boldsymbol{\theta}) \times p(\boldsymbol{\theta})]d\boldsymbol{\theta} \end{aligned}
•
marginal likelihood는 log가 식 안으로 들어갈 수 없기 때문에, log를 취해서 덧셈으로 변환할 수 없다.
•
만일 특정 파라미터 θk\theta_k에 대해 marginal likelihood를 구한다면 다음과 같이 작성해서 계산할 수 있다.
◦
위는 이산인 경우, 아래는 연속인 경우.
p(θk∣D)=∑θ−k[p(D∣θ)×p(θ)]p(θk∣D)=∫[p(D∣θ)×p(θ)]dθ−k\begin{aligned} p(\theta_k|\mathcal{D}) &= \sum_{\boldsymbol{\theta}_{-k}} [p(\mathcal{D}|\boldsymbol{\theta}) \times p(\boldsymbol{\theta})] \\ p(\theta_k|\mathcal{D}) &= \int [p(\mathcal{D}|\boldsymbol{\theta}) \times p(\boldsymbol{\theta})]d\boldsymbol{\theta}_{-k}\end{aligned}
•
흥미롭게도 log marginal likelihood는 모델 평가에 대한 leave-one-out cross validation(LOO-CV)의 log likelihood와 가깝게 연관되어있다.

Posterior mean, variance

•
mode는 전체 분포에서 단일 점을 고르는 것에 해당하므로 분포를 제대로 요약하지 못한다. 좀 더 견고한 값은 평균(mean)이다.
◦
prior와 likelihood가 켤레(conjugate)일 때, posterior의 mean은 prior의 mean과 likelihood의 mode(MLE)의 볼록 결합(convex combination)으로 표현 가능하다.
•
추정치의 불확실성을 포착하기 위해 표준 오차(standard error)를 계산할 수 있는데, 베이지안 통계에서 이것은 posterior의 표준 편차(standard deviation)으로 계산된다.
se(θ)=V[θ∣D]\text{se}(\theta) = \sqrt{\mathbb{V}[\theta|\mathcal{D}]}

Credible intervals

•
posterior 분포는 고차원 객체이기 때문에 이것을 요약하는 일반적인 방법은 posterior의 평균이나 최빈값 같은 점 추정치를 구한 다음에 이 추정치에 연관된 불확실성을 정량화하는 credible interval(신뢰 구간)을 계산하는 것이다.
•
더 정확하게 100(1−α)100(1-\alpha)% 신뢰 구간을 posterior 확률 질량의 1−α1-\alpha을 포함하는 (인접한) 영역 C=(ℓ,u)C = (\ell,u) (lower와 upper의 약자이다) 으로 정의한다.
Cα(D)=(ℓ,u):P(ℓ≤θ≤u∣D)=1−αC_\alpha(\mathcal{D}) = (\ell,u) : P(\ell \le \theta \le u|\mathcal{D}) = 1-\alpha
•
위 식을 만족하는 많은 구간이 있을 수 있기 때문에 일반적으로 각 꼬리에서 질량이 (1−α)/2(1-\alpha)/2인 구간을 선택한다. 이것을 central interval(중심 구간)이라고 한다.
◦
posterior가 알려진 함수 형식을 가지면 ℓ=F−1(α/2)\ell = F^{-1}(\alpha/2)와 u=F−1(1−α/2)u = F^{-1}(1-\alpha/2)를 사용하여 posterior central interval을 계산할 수 있다. 여기서 FF는 posterior의 cdf이고 F−1F^{-1}은 inverse cdf이다.
◦
만일 posterior가 가우시안 p(θ∣D)=N(0,1)p(\theta|\mathcal{D}) = \mathcal{N}(0,1)이고 α=0.05\alpha=0.05이면 ℓ=Φ−1(α/2)=−1.96\ell = \Phi^{-1}(\alpha/2) = -1.96이고 u=Φ−1(1−α/2)=1.96u = \Phi^{-1}(1-\alpha/2) = 1.96이 된다. 여기서 Φ\Phi는 가우시안의 cdf 표기이다.
◦
이것은 μ±2σ\mu \pm 2\sigma 형식의 신뢰 구간을 인용하는 일반적인 사용을 나타낸다. 여기서 μ\mu는 posterior 평균을 나타내고 σ\sigma는 posterior 표준편차를 나타내고 22는 1.961.96에 대한 좋은 근사치이다.
•
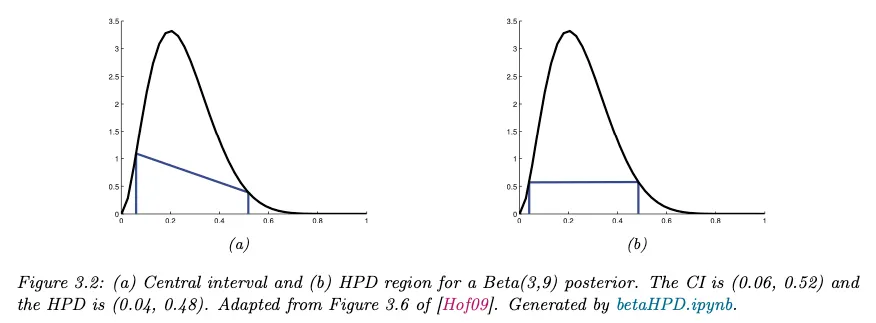
중심 구간의 문제는 구간 내부보다 외부에 많은 점들이 있을 수 있다는 것이다. 이 때문에 어떤 임계치(threshold) 보다 높은 확률을 갖는 점들의 집합인 highest posterior density(HPD)를 사용한다. 더 정확하게 다음과 같은 pdf 위의 임계치 p∗p^*를 찾는다.
1−α=∫θ:p(θ∣D)>p∗p(θ∣D)dθ1 - \alpha = \int_{\theta:p(\theta|\mathcal{D}) > p^*}p(\theta|\mathcal{D})d\theta
•
그 다음 HPD를 다음처럼 정의한다.
Cα(D)={θ:p(θ∣D)≥p∗}C_\alpha(\mathcal{D}) = \{\theta:p(\theta|\mathcal{D}) \ge p^*\}
•
1차원의 경우 HPD 영역은 highest density interval(HDI)라고 부른다.
◦
아래 그림 (b)는 Beta(3,9)\text{Beta}(3,9) 분포의 95% HDI (0.04,0.48)(0.04,0.48)를 보여준다. 이것이 질량의 95%를 포함함에도 중심 구간보다 좁다는 것을 볼 수 있다. 게다가 내부의 모든 점이 외부의 모든 점보다 밀도가 높다.

Posterior predictive distribution

•
미래 관측을 예측하기 위해 알려지지 않은 파라미터들을 모두 marginalizing out해서 posterior predictive distribution을 계산할 수 있다.
p(y∣D)=∫p(y∣θ)p(θ∣D)dθp(\bold{y}|\mathcal{D}) = \int p(\bold{y}|\boldsymbol{\theta})p(\boldsymbol{\theta}|\mathcal{D})d\boldsymbol{\theta}
•
이 적분은 계산하기 어렵기 때문에 파라미터의 점 추정치 θ^=δ(D)\hat{\boldsymbol{\theta}} = \delta(\mathcal{D})를 plug in 하여 근사치를 구할 수 있다. 여기서 δ()\delta()는 MLE나 MAP를 계산하는 방법과 같은 추정기이다.
p(y∣D)≈p(y∣θ^)p(\bold{y}|\mathcal{D}) \approx p(\bold{y}|\hat{\boldsymbol{\theta}})
•
이것을 plugin approximation이라고 한다. 이것은 점 추정치를 중심으로 한 degenerate 분포로 posterior를 모델링하는 것과 동등하다.
•
불행히 plugin 근사는 과적합될 수 있다. 플러그인 근사 대신 정확한 posterior 예측을 계산하기 위해 모든 파라미터 값을 marginalize 할 수 있다.

Marginal likelihood

•
모델 M\mathcal{M}에 대한 marginal likelihood (evidence라고도 함)는 다음과 같이 정의된다.
p(D∣M)=∫p(θ∣M)p(D∣θ,M)dθp(\mathcal{D}|\mathcal{M}) = \int p(\boldsymbol{\theta}|\mathcal{M})p(\mathcal{D}|\boldsymbol{\theta},\mathcal{M})d\boldsymbol{\theta}
•
특정한 모델의 파라미터에 대한 추론을 수행할 때, 이 항은 θ\boldsymbol{\theta}에 관해 상수이기 때문에 이 항을 무시할 수 있다.
◦
그러나 이 수량은 두 모델 사이를 선택할 때 필수적인 역할을 수행한다. 이것은 데이터로부터 하이퍼파라미터를 추정할 때도(empirical Bayes라고 부르는 접근) 유용하다.
•
일반적으로 marginal likelihood를 계산하는 것은 어렵다.
◦
그러나 베타-베르누이 모델의 경우에 marginal likelihood는 posterior normalizer와 prior normalizer의 비율에 비례한다.

Modeling more complex data

•
베이지안 접근을 더 복잡한 모델에도 적용할 수 있다. 예컨대 머신러닝에서 입력 feature x\bold{x}가 주어지면 출력 y\bold{y}를 예측하는데 매우 관심이 있다. 이를 위해 p(y∣x,θ)p(\bold{y}|\bold{x},\boldsymbol{\theta}) 형식의 조건부 확률 분포를 사용할 수 있다. 이것은 선형 모델나 신경망 등으로 일반화될 수 있다.
•
관심있는 주요 수량은 다음과 같이 주어지는 posterior 예측 분포이다.
p(y∣x,D)=∫p(y∣x,θ)p(θ∣D)dθp(\bold{y}|\bold{x},\mathcal{D}) = \int p(\bold{y}|\bold{x},\boldsymbol{\theta})p(\boldsymbol{\theta}|\mathcal{D})d\boldsymbol{\theta}
•
알려지지 않은 파라미터를 적분하거나 marginalizing out하여 무한한 수의 모델로부터 예측의 가중 평균을 효과적으로 계산하기 때문에 과적합의 가능성을 줄인다.
◦
불확실성을 적분하는 행위는 머신러닝에 대한 베이지안 접근의 핵심이다.
•
베이지안 접근을 더 일반적인 플러그인 근사와 대비하는 것은 가치가 있다. 여기서는 파라미터의 점 추정 θ^\hat{\boldsymbol{\theta}}을 계산하고(MLE 같이) 그것을 p(y∣x,θ^)p(\bold{y}|\bold{x},\hat{\boldsymbol{\theta}})을 사용하여 모델에 연결하여 예측을 만든다.
◦
플러그인 근사는 단순하고 널리 사용되지만 그러나 파라미터 추정에서 불확실성을 무시하므로 예측 불확실성이 과소추정(underestimate)될 수 있다.

Exchangeability and de Finetti’s theorem

•
베이지안 접근에 대한 흥미로운 철학적인 질문은 이것이다. ‘prior는 어디서 오는가?’ 이것은 모델의 추상적인 수량일 뿐이고, 직접 관찰할 수 없는 파라미터를 참조한다.
◦
de Finetti’s theorem이라 하는 근본적인 결과는 이러한 파라미터가 관찰 가능한 결과에 대한 믿음과 어떻게 연관되었는지를 설명한다.
•
결과를 설명하기 위해 우선 정의를 해야 한다.
◦
임의의 nn에 대해 결합 확률 p(x1,...,xn)p(\bold{x}_1,...,\bold{x}_n)의 index가 순열에 불변이면 확률 변수들의 시퀀스 (x1,x2,...)(\bold{x}_1,\bold{x}_2,...)를 infinitely exchangeable(교환 가능)이라고 한다. 즉 모든 순열 π\pi에 대해 다음이 성립한다.
p(x1,...,xn)=p(xπ1,...,xπn)p(\bold{x}_1,...,\bold{x}_n) = p(\bold{x}_{\pi_1},...,\bold{x}_{\pi_n})
•
교환가능은 iid(independent, identically distribute) 변수의 시퀀스라는 더 친숙한 개념에 비해 더 일반화된 개념이다.
◦
예컨대 D=(x1,...,xn)\mathcal{D} = (\bold{x}_1,...,\bold{x}_n)가 이미지의 시퀀스라고 가정한다. 여기서 xi∼p∗\bold{x}_i \sim p^*는 ‘실제 분포’ p∗p^*에서 독립적으로 생성된다. 이것이 iid 시퀀스임을 알 수 있다.
◦
이제 x0\bold{x}_0가 background 이미지라고 가정하자. 시퀀스 (x0+x1,...,x0+xn)(\bold{x}_0 + \bold{x}_1,...,\bold{x}_0+\bold{x}_n)은 무한히 교환가능하지만 iid는 아니다. 모든 변수들이 숨겨진 공통 요소 즉 background x0\bold{x}_0를 공유하기 때문이다.
◦
따라서 더 많이 볼수록 공유된 x0\bold{x}_0를 더 잘 추정할 수 있으므로 미래 요소를 더 잘 예측할 수 있다.
•
더 일반적으로 교환 가능 시퀀스를 숨겨진 공통 원인에서 비롯한 것으로 볼 수 있고 이를 알려지지 않은 확률 변수 θ\boldsymbol{\theta}로 처리할 수 있다. 이것은 de Finetti’s theorem으로 형식화될 수 있다.
de Finetti’s theorem. 확률 변수들의 시퀀스 (x1,x2,...)(\bold{x}_1,\bold{x}_2,...)는 다음과 같이 모든 nn에 대해 무한히 교환 가능하고, 그 역도 성립한다.
p(x1,...,xn)=∫∏i=1np(xi∣θ)p(θ)dθp(\bold{x}_1,...,\bold{x}_n) = \int \prod_{i=1}^n p(\bold{x}_i|\boldsymbol{\theta})p(\boldsymbol{\theta})d\boldsymbol{\theta}
여기서 θ\boldsymbol{\theta}는 어떤 숨겨진 공통 확률 변수(아마도 무한 차원)이다. 즉 xi\bold{x}_i는 θ\boldsymbol{\theta}에서 조건부 iid이다.
•
종종 θ\boldsymbol{\theta}를 파라미터로 해석한다. 이 정리에 따르면 데이터가 교환 가능하면 반드시 파라미터 θ\boldsymbol{\theta}, likelihood p(xi∣θ)p(\bold{x}_i|\boldsymbol{\theta}), prior p(θ)p(\boldsymbol{\theta})가 반드시 존재한다. 따라서 베이지안 접근은 교환 가능성으로부터 자동으로 따라온다.
◦
이 접근법은 partially exhangeable(부분적으로 교환 가능)이라는 개념을 사용하여 조건부 확률 모델을 확장할 수도 있다.

참고

Made with