Search
Duplicate

수학/ Invertible Transformations, Monte Carlo, PIT

Invertible transformations (bijections)

•
ff가 Rn→Rn\mathbb{R}^n \to \mathbb{R}^n인 전단사(bijection)라고 하자.
◦
전단사는 단사(injective), 즉 one-to-one이고 전사(surjective)인 함수이다. 이것은 함수가 역이 잘 정의되었다는 것을 의미한다.
•
y=f(x)\bold{y} = f(\bold{x})의 pdf를 계산하기 원한다고 가정하자. change of variables 공식은 다음을 말한다.
py(y)=px(f−1(y))∣det⁡[Jf−1(y)]∣p_y(\bold{y}) = p_x(f^{-1}(\bold{y}))|\det[\bold{J}_{f^{-1}}(\bold{y})]|
•
여기서 Jf−1(y)\bold{J}_{f^{-1}}(\bold{y})는 y\bold{y}에서 계산된 역행렬 f−1f^{-1}의 야코비안이다. 그리고 ∣det⁡J∣|\det \bold{J}|는 J\bold{J}의 determinant(행렬식)의 절대값이다. 즉
Jf−1(y)=(∂x1∂y1…∂x1∂yn⋮∂xn∂y1…∂xn∂yn)\bold{J}_{f^{-1}}(\bold{y}) = \begin{pmatrix} {\partial x_1 \over \partial y_1} & \dots & {\partial x_1 \over \partial y_n} \\ & \vdots & \\ {\partial x_n \over \partial y_1} & \dots & {\partial x_n \over \partial y_n}\end{pmatrix}
•
야코비안 행렬이 삼각이면 행렬식은 주 대각 항들의 곱으로 축소된다.
det⁡(J)=∏i=1n∂xi∂yi\det(\bold{J}) = \prod_{i=1}^n {\partial x_i \over \partial y_i}

Monte Carlo approximation

•
때때로 야코비안을 계산하는 것이 어려울 수 있다. 이 경우에 Monte Carlo 근사를 만들 수 있다. SS개의 샘플 xs∼p(x)\bold{x}^s \sim p(\bold{x})를 뽑고 ys=f(xs)\bold{y}^s = f(\bold{x}^s)를 계산한 다음 경험적 pdf를 구성하면 된다.
pD(y)=1S∑s=1Sδ(y−ys)p_\mathcal{D}(\bold{y}) = {1\over S} \sum_{s=1}^S \delta(\bold{y} - \bold{y}^s)
•
예컨대 x∼N(6,1)x \sim \mathcal{N}(6,1)이고 y=f(x)y = f(x)이고 f(x)=11+exp⁡(−x+5)f(x) = {1\over 1 + \exp(-x+5)}라 하면 몬테 카를로를 사용하여 p(y)p(y)를 근사할 수 있다.

Probability integral transform

•
XX가 cdf PXP_X의 확률 변수라 하고 Y(X)=PX(X)Y(X) = P_X(X)를 XX의 변환이라고 하자. 이제 YY가 균등 분포를 가지면 결과는 probability integral transform(PIT)임을 볼 수 있다.
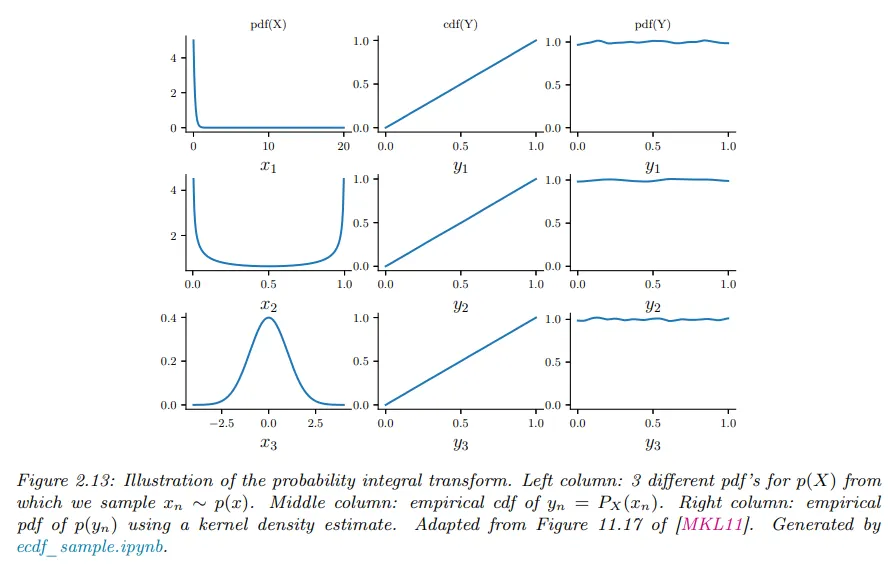
PY(y)=Pr(Y≥y)=Pr(PX(X)≤y)=Pr(X≤PX−1(y))=PX(PX−1(y))=y\begin{aligned} P_Y(y) &= \text{Pr}(Y \ge y) = \text{Pr}(P_X(X) \le y) \\ &= \text{Pr}(X \le P_X^{-1}(y)) = P_X(P_X^{-1}(y)) = y \end{aligned}
•
예컨대 아래 그림 왼쪽 열에서 pdf의 pXp_X의 다양한 분포를 볼 수 있다.
◦
이것으로부터 샘플링하면 xn∼pxx_n \sim p_x를 얻는다. 다음으로 yn=PX(xn)y_n = P_X(x_n)을 계산한 다음 값을 정렬하여 Y=PX(X)Y = P_X(X)의 경험적 cdf를 계산한다. 결과는 중간 열에 보인다. 이 분포가 균등임을 보일 수 있다.
◦
또한 커널 밀도 추정을 사용하여 YY의 pdf를 근사할 수 있다. 이것은 오른쪽 열에 보인다. 그리고 이것이 (근사적으로) 편평함을 볼 수 있다.
•
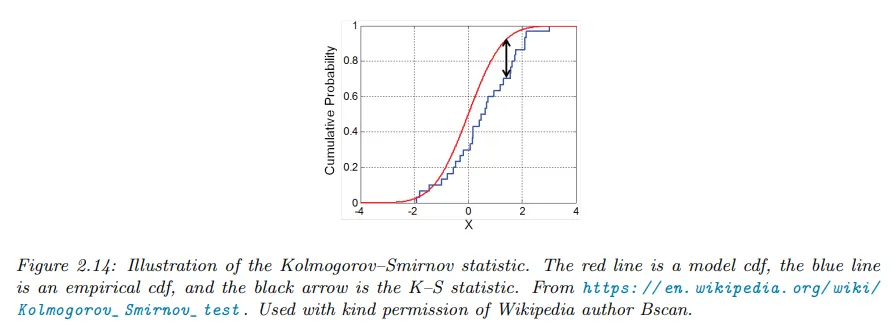
Kolmogorov-Smirnov test를 사용하여 샘플들의 집합이 주어진 분포에서 나왔는지 테스트하기 위해 PIT를 사용할 수 있다. 이것을 하기 위해 샘플들의 경험적 cdf와 분포의 이론적 cdf를 plot하고 이 두 커브 사이의 최대 거리를 계산한다. 아래 그림 참조.
•
형식적으로 KS 통계량은 다음처럼 정의된다.
Dn=max⁡x∣Pn(x)−P(x)∣D_n = \max_x |P_n(x) - P(x)|
•
여기서 nn은 샘플 크기이고
◦
PnP_n은 경험적 cdf이고
◦
PP는 이론적 cdf이다.
•
샘플이 PP로부터 뽑힌 경우 값 DnD_n은 0에 접근해야 한다(n→∞)n \to \infty).
•
PIT의 또 다른 응용은 분포에서 샘플을 생성하는 것이다. 균등 분포 un∼Unif(0,1)u_n \sim \text{Unif}(0,1)에서 샘플링하는 방법이 있으면, xn=PX−1(un)x_n = P_X^{-1}(u_n)를 설정하여 이것을 cdf PXP_X가 있는 다른 분포의 샘플로 변환할 수 있다.

참고

Made with