Search
Duplicate

AI/ Camera Transformation, Intrinsic, Extrinsic

Camera Matrix Model

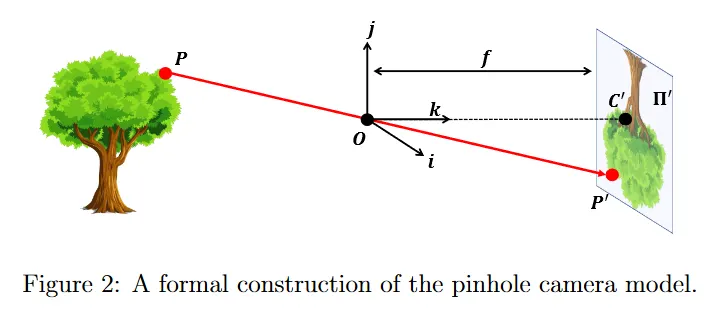
카메라 행렬 모델은 월드 점 PP를 이미지 좌표 P′P'에 매핑하는 파라미터 집합을 행렬 형태로 표현한 것이다. 우선 아래 그림과 같이 월드 점 PP와 이미지 좌표 P′P'의 관계를 살펴보자. 월드 좌표를 P=(x,y,z)P = (x, y, z)라 하고 그것에 대응하는 이미지 좌표 P′=(x′,y′,z′)P' = (x', y', z')라 하자.
위 그림에서 원점 OO를 중심으로 PP에 해당하는 삼각형 (0,0,0),(x,y,0),(0,0,z)(0, 0, 0), (x, y, 0), (0, 0, z)와 P′P'에 해당하는 삼각형 (0,0,0),(x′,y′,0),(0,0,z′)(0, 0, 0), (x', y', 0), (0, 0, z')는 닮음 관계이다. 따라서 삼각형의 닮음 관계를 따라 x′x'와 y′y'는 각각 xx와 yy에 대해 z′z{z' \over z}의 비율을 곱한 값으로 구할 수 있다.
x′=x⋅z′z=x⋅fz=f⋅xzy′=y⋅z′z=y⋅fz=f⋅yz\begin{aligned} x' = x \cdot {z' \over z} = x \cdot {f \over z} = f \cdot {x \over z} \\ y' = y \cdot {z' \over z} = y \cdot {f \over z} = f \cdot {y \over z} \end{aligned}
여기서 z′z'는 focal length ff에 해당하므로 z′=fz' = f로 치환하고 이후 유도의 편의를 위해 ff와 x,yx, y의 자리를 바꾸어 최종적으로 아래와 같이 정리한다.
P′=[x′y′]=[f⋅xzf⋅yz]P' = \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} f \cdot {x \over z} \\ f \cdot {y \over z} \end{bmatrix}
월드 점 PP의 원점은 이미지의 중심에 있는 반면, 이미지 좌표의 원점은 왼쪽 아래 또는 왼쪽 위를 원점으로 한다. 따라서 원점을 이미지 좌표의 원점 만큼 평행이동 시키는 cx,cyc_x, c_y를 위의 식에 추가한다.
P′=[x′y′]=[f⋅xz+cxf⋅yz+cy]P' = \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} f \cdot {x \over z} + c_x \\ f \cdot {y \over z} + c_y \end{bmatrix}
다음으로 월드 점은 물리적 측정 단위(mm, cm 등)을 사용하는데 반해, 이미지 점의 단위는 pixel을 사용한다. 이를 반영하여 pixelscm{\text{pixels} \over \text{cm}}와 같은 단위 변환에 해당하는 파라미터를 추가한다. 이때 이미지 픽셀의 aspect ratio(종횡비)가 1이 되지 않을 수 있기 때문에 xx축과 yy축에 대해 각각 kk와 ll의 파라미터를 사용한다. k=lk = l이면 square pixel을 가졌다고 한다.
P′=[x′y′]=[fkxz+cxflyz+cy]=[αxz+cxβyz+cy]P' = \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} fk{x \over z} + c_x \\ fl{y\over z} + c_y \end{bmatrix} = \begin{bmatrix} \alpha{x \over z} + c_x \\ \beta{y\over z} + c_y \end{bmatrix}
여기서 초점거리 ff와 단위 변환 파라미터 k,lk, l는 고정된 값이므로 합쳐서 단일 파라미터 α,β\alpha, \beta로 만든다.

Homogeneous Coordinate

위의 Camera Matrix 모델은 입력을 파라미터 중 하나인 zz로 나누는 연산이 포함되어 있기 때문에 선형이 아니다. 이를 해결하기 위해 homogeneous 좌표계를 도입한다. 이를 이용하면 좌표 변환을 행렬-벡터 형식으로 나타낼 수 있게 된다.
homogeneous 좌표계는 기존의 점에 대해 차원을 1개 추가하여 표현하는 것이다. 예컨대 2차원 점 P=(x,y)P = (x, y)를 (x,y,1)(x, y, 1)로 표현하고, 3차원 점 P=(x,y,z)P = (x, y, z)을 (x,y,z,1)(x, y, z, 1)로 표현하는 것이다.
임의의 유클리트 벡터 (v1,...,vn)(v_1, ..., v_n)에 대해 homogeneous 좌표 (v1,...,vn,w)(v_1, ..., v_n, w)로 변환 할 수 있다. 이 homogeneous 좌표를 다시 유클리드 좌표로 다시 변환하면 (v1w,...,vnw)({v_1\over w}, ..., {v_n\over w})가 된다. 따라서 w=1w=1인 경우 homogeneous 좌표 (v1,...,vn,1)(v_1, ..., v_n, 1)와 유클리드 좌표 (v1,...,vn)(v_1, ..., v_n)는 동일하다.
homogeneous 좌표계를 사용하여 Camera 행렬 모델에서 이미지 점 P′P'를 다음과 같이 표현할 수 있다.
P′=[αx+cxzβy+cyzz]=[α0cx00βcy00010][xyz1]=[α0cx00βcy00010]P=MPP' = \begin{bmatrix} \alpha x + c_x z \\ \beta y + c_y z \\ z \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} P = MP
(위 식의 2번째 식은 homogeneous를 유클리드 좌표로 다시 변환할 때 (v1w,...,vnw)({v_1\over w}, ..., {v_n\over w})라는 점을 따른다.)
위의 변환을 다음처럼 분해할 수 있다.
P′=MP=[x′y′z]=[α0cx0βcy001][I0]=K[I0]PP' = MP = \begin{bmatrix} x' \\ y' \\ z \end{bmatrix} = \begin{bmatrix} \alpha & 0 & c_x \\ 0 & \beta & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} I & 0 \end{bmatrix} = K \begin{bmatrix} I & 0 \end{bmatrix} P
여기서 행렬 KK를 camera matrix라고 부른다. 카메라 행렬에 대해 다음과 같이 α,β\alpha, \beta 대신 fx,fyf_x, f_y를 사용하여 표현하는 경우도 있다.
K=[fx0cx0fycy001]K = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}
카메라 행렬의 마지막 행이 [00...1][0 \quad 0 \quad ... \quad 1]의 형식이기 때문에 Affine transformation의 형식이 된다.

Intrinsic Parameters

위의 카메라 행렬 KK에는 2개의 offset cx,cyc_x, c_y와 2개의 focal length α,β\alpha, \beta가 포함되어 총 4개의 파라미터를 갖는다. 여기에 skewness를 추가하면 5개의 자유도가 되며, 이를 카메라의 Intrinsic Parameter라고 하며 다음과 같이 정의된다.
K=[x′y′z]=[α−αcot⁡θcx0βsin⁡θcy001]K = \begin{bmatrix} x' \\ y' \\ z \end{bmatrix} = \begin{bmatrix} \alpha & -\alpha \cot \theta & c_x \\ 0 & {\beta \over \sin \theta} & c_y \\ 0 & 0 & 1 \end{bmatrix}
이것은 카메라가 공장에서 물리적으로 생산될 때 카메라에 내재된 설정이 된다.
만일 카메라카멜라에서 일반적으로 skewness는 거의 없다고 가정하며 θ=π/2=90\theta = \pi /2 =90도 설정한다. 이 경우 cot⁡90=0,sin⁡90=1\cot 90 = 0, \sin 90 = 1이므로 focal length와 center만 존재하는 카메라 행렬을 복구하게 된다.

Extrinsic Parameters

카메라의 내재된 정보가 아니라, 카메라 자체의 움직임에 의해 발생하는 정보—일반적으로 카메라의 연속 프레임 사이의 차이가 된다—가 존재할 때, 즉 카메라 자체가 translation(평행이동) 하거나 rotation(회전) 할 때 월드 점 PP를 이미지 점 P′P'에 매핑하기 위해 다음과 같은 변환을 사용할 수 있다.
P′=[RT01]PwP' = \begin{bmatrix} R & T \\ 0 & 1 \end{bmatrix}P_w
여기서 RR은 R⊤R=IR^\top R = I를 만족하는 3×33 \times 3 Rotation matrix이고
R=[r11r12r13r21r22r23r31r32r33]R = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix}
TT는 translation vector이고
T=[txtytz]T = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}
PwP_w는 homogeneous world 좌표이다.
Pw=[XwYwZw1]P_w = \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}
따라서 전체 식은 다음과 같이 작성된다.
P=[RT01]Pw=[r11r12r13txr21r22r23tyr31r32r33tz0001][XwYwZw1]P = \begin{bmatrix} R & T \\ 0 & 1 \end{bmatrix}P_w = \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}
RR과 TT는 카메라에 의존하지 않고 외부에 존재하기 때문에 extrinsic parameter라고 한다.
카메라 행렬을 이용하여 위의 식을 다음과 같이 단순화 할 수 있다.
P′=K[RT]Pw=MPwP' = K \begin{bmatrix} R & T \end{bmatrix}P_w = MP_w
이것은 다음처럼 계산된다.
P′=[α−αcot⁡θcx0βsin⁡θcy001][r11r12r13txr21r22r23tyr31r32r33tz]⏟M∈R3×4[XwYwZw1]P' =\underbrace{\begin{bmatrix} \alpha & -\alpha \cot \theta & c_x \\ 0 & {\beta \over \sin \theta} & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \end{bmatrix}}_{M \in \mathbb{R}^{3\times4}} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}
여기서 투영 행렬 M∈R3×4M \in \mathbb{R}^{3 \times 4}은 intrinsic과 extrinsic 파라미터로 구성되며, 총 11개의 자유도를 갖는다. 5개는 intrinsic 카메라 행렬에서 오고, 3개는 rotation에서 오고, 3개는 translation에서 온다.
일반적으로 단일 카메라 설정에서 rotation과 translation은 해당 카메라의 연속 프레임 사이에 존재하는 회전과 평행이동을 나타내지만, stereo 카메라 설정을 사용하는 경우 rotation과 translation은 두 카메라 사이의 상대적 rotation과 translation을 의미한다. 물론 stereo 카메라 자체가 rotation과 translation 변화를 갖는다면, 추가로 별도의 rotation과 translation을 구해야 한다.

Rotation Matrix

Rotation 행렬을 각 축 별로 다음과 같이 표현한다. 여기서 α,β,γ\alpha, \beta, \gamma는 x,y,zx, y, z축의 회전 각도를 의미한다.
Rx(α)=[1000cos⁡α−sin⁡α0sin⁡αcos⁡α]Ry(β)=[cos⁡β0sin⁡β010−sin⁡β0cos⁡β]Rz(γ)=[cos⁡γ−sin⁡γ0sin⁡γcos⁡γ0001]\begin{aligned} R_x(\alpha) &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \alpha & - \sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{bmatrix} \\ R_y(\beta) &= \begin{bmatrix} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{bmatrix} \\ R_z(\gamma) &= \begin{bmatrix} \cos \gamma & -\sin\gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{aligned}
행렬 곱의 관계 때문에 행렬곱 RxRyRzR_xR_yR_z에 따라 회전은 처음에 z축을 따라 회전한 후, y축, 그 다음 x축으로 회전하여 얻을 수 있다.

Translation Matrix

translation을 벡터가 아니라 homogeneous 좌표를 따르는 행렬 형식으로 다음과 같이 표현할 수 있다.
T=[100tx010ty001tz0001]T = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}

Scale Matrix

방향에 따라 어떤 양 Sx,Sy,SzS_x, S_y, S_z으로 벡터를 scale 하기를 원하면 다음과 같은 scale matrix를 구성할 수 있다.
S=[Sx000Sy000Sz]S = \begin{bmatrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & S_z \end{bmatrix}
따라서 만일 벡터를 scale 한 다음 rotate하고 마지막으로 translate 하는 변환 행렬은 다음이 된다.
T=[RSt01]T = \begin{bmatrix} RS & t \\ 0 & 1 \end{bmatrix}

참고

Made with